Конечно-элементный анализ эффективности установки вкладки для замещения дефекта премоляра
Автор: Кирюхин В.Ю., Рогожников Г.И., Шулятникова О.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (35) т.11, 2007 года.
Бесплатный доступ
В данной работе на основании конечно-элементного моделирования рассматривается работа вкладки, замещающей обширный дефект эмали зуба. Предполагается, что вкладка изготовлена из циркония и укреплена в зубе с помощью цемента. Анализируются два вида формы поверхности контакта вкладки зуба: плоская и пазообразная. Также предлагаются варианты нагружения вкладки (температурное и силовое) для сравнения и выделения наиболее опасного воздействия с позиции последующих возможных осложнений. В результате показано, что температурное воздействие имеет большее влияние на состояние вкладки и окружающие ее ткани, нежели силовое. Использование дополнительного паза в теле вкладки позволяет снизить пиковые напряжения в тех областях, в которыx наиболее часто возникают осложнения.
Восстановление зубов, вкладка, проектирование, цирконий, метод конечных элементов
Короткий адрес: https://sciup.org/146215882
IDR: 146215882 | УДК: 531/534:
Текст научной статьи Конечно-элементный анализ эффективности установки вкладки для замещения дефекта премоляра
При возникновении больших дефектов жевательной поверхности зуба (сколы, обширный и глубокий кариес) в современной стоматологии применяют технологию установки вкладки. Суть данного метода состоит в том, что сначала удаляют причины поражения, трещины и пр. Затем пораженную область обрабатывают, придавая удобную для дальнейших манипуляций форму. После этого подготавливается фрагмент (вкладка) из какого-либо искусственного материала, который с помощью цемента устанавливается в подготовленную полость, восстанавливая тем самым полностью поверхность зуба. Вкладка может быть изготовлена по форме подготовленной полости, а также иметь стандартную форму, приданную изготовителем. Тогда полость готовится под имеющуюся вкладку.
Огромный опыт установки вкладок не избавил этот тип восстановления поверхности зуба от ряда негативных последствий: выпадение вкладки (расцементирование), откол эмали зуба, возникновение кариеса на поверхности эмали в области ее контакта с материалом вкладки и пр. Тогда кажется очевидной актуальность анализа и последующего проектирования формы и материала вкладки, способа ее крепления с целью минимизировать вероятность появления приведенных выше нежелательных осложнений.
Рассмотрение данной проблемы с позиций биомеханики началось достаточно давно. Одной из первых работ в этой области стало исследование по применению металлических вкладок для восстановления молочных зубов [1]. Причем практика многих лет продемонстрировала эффективность использования для изготовления вкладок таких металлов, как сплавы золота, титана [2–4]. Представленные в этих исследованиях результаты показали, что, в принципе, существенных различий между металлами с точки зрения механической эффективности при работе вкладки не существует. При этом такие материалы, как титан или золото, достаточно практичны при использовании в клинике наряду с полимеризационными композиционными материалами [5].
Вместе с тем, в последнее время отмечается огромный исследовательский интерес к применению материалов неметаллической природы [6]. Однако до сих пор в научной литературе не приведено доказательств полного преимущества в использовании того или иного типа материалов (металлов или композитов). Очевидно, те и другие имеют свои положительные качества, которые принимает во внимание практикующий врач при принятии решения.
В последнее время в ортопедической стоматологии стал активно использоваться цирконий. Обладая хорошими свойствами в отношении биологической инертности, он имеет высокие механические свойства (см. далее таблицу) и удобнее в клинической практике [5]. Поэтому авторы данной работы предлагают обратиться к анализу работы вкладки, изготовленной из такого материала.
Дополнительной особенностью исследования практических задач стоматологии с позиции биомеханики является выделение фактора, воздействующего на объект анализа: силовой и/или температурный. В действительности, до сих пор остается не выясненным до конца вопрос, какой из них оказывает наибольшее влияние на запуск и протекание процессов разрушения. Так, многочисленные исследователи, к примеру [7– -9], рассчитывают поведение зубочелюстной модели под воздействием силового нагружения, вызванного жеванием. Намного скромнее список работ, к примеру [10], в которых рассматривается температурное воздействие. Однако на основании результатов упомянутых исследований не следует, что тепловое или силовое воздействие играет преобладающую роль, на которую нужно ориентироваться при проектировании того или иного метода лечения какого-то поражения или заболевания в области зубов и окружающих их тканей. Правда, следует отметить, что «чистое» силовое воздействие рассматривается в таких работах чаще.
Конечно, учет обоих факторов нагружения приводит к наиболее адекватным результатам анализа состояния тканей зубочелюстной системы. Однако в этих условиях попытка спроектировать операцию или параметры применяемых при лечении средств (материалы, размеры области, способ фиксации и пр.) оборачивается в лучшем случае возрастающей сложностью. Но и не исключена ситуация, когда учет факторов температуры и силы приводит к противоречивым тенденциям при проектировании. Например, использование твердых сплавов металлов для замещения дефектов эмали зуба оправдано с точки зрения деформационной совместимости и прочности в условиях силового нагружения. Однако давно показано в теории [11] и на практике [5], что такая комбинация материалов приводит к резким негативным последствиям из-за температурной несовместности титана и эмали, выраженной в большом различии значений коэффициентов линейного температурного расширения. И наоборот, применение материалов, близких по теплопроводным свойствам к соседствующим живым тканям (стекловолоконные материалы, к примеру), имеет тенденцию к более низкому качеству по реакции на интенсивное или долговременное силовое нагружение.
Поэтому авторы данной работы считают актуальным сравнить, воздействие какого из факторов (температура или сила) соответствует картине осложнений, наиболее часто наблюдаемых на практике, в долгосрочной [12] или краткосрочной перспективе [13].
Цели работы
В данной работе на основе механического анализа предлагается исследовать основные причины, приводящие к негативным последствиям установки вкладки. А именно: какой из механических факторов (сила или температура) оказывает наибольшее негативное воздействие на состояние эмали, и как влияет на качество установки вкладки использование паза.
Поэтому в рамках настоящего механического исследования авторы ставят целью следующие вопросы:
-
1) сравнить напряженное состояние целого зуба как механической конструкции под действием жевательной нагрузки и под действием температуры,
-
2) провести аналогичное сравнение для восстановленного вкладкой зуба без паза и с пазом.
Для решения этой проблемы предлагается следующая последовательность действий.
-
1. Создать трехмерную геометрическую модель расчетной схемы моляра по выбранному образцу. Задать размеры и расположение циркониевой вкладки. Задать тип цементирующего материала и его толщину между зубом и вкладкой.
-
2. Смоделировать на основе теории термоупругости процесс силового нагружения и нагрева системы зуб–вкладка. Использовать при этом численный метод конечных элементов как хорошо зарекомендовавший себя в решении задач биомеханики в стоматологии.
-
3. Провести анализ результатов расчета, а именно:
-
• продемонстрировать напряженно-деформированное состояние зуба и отдельных его компонентов при указанных вариантах нагрузки;
-
• провести качественное сравнение различных показателей напряженного состояния и выделить отличия в силовом или температурном нагружении, при использовании паза или без него;
-
• указать наиболее опасные зоны (по величине напряжений и деформаций).
Модель зуба как биомеханической системы
Структура расчетной схемы
Для расчета предлагается модель, полученная по реальным размерам премоляра (двухкорневого зуба). В рассматриваемую расчетную схему включены следующие элементы: зуб, сама вкладка и фиксирующий ее цемент. Зуб представлен в виде конструкции из эмали и дентина, в которых подготовлены полости для установки вкладки, см. рис.1. На рис. 2 показана сборка модели с условно разнесенными частями. Формы цемента и вкладки проиллюстрированы на данных диаграммах с подготовленным пазом, который по предположению авторов, с одной стороны, должен улучшить качество фиксации вкладки. С другой стороны, он призван увеличить скорость теплообмена между вкладкой и сохранившимися тканями зуба. Никакие иные компоненты (альвеолярный отросток, нижняя челюсть, зубы–антагонисты) зубочелюстной системы в данной работе не рассматриваются, поскольку они либо достаточно удалены от области интересов исследования (вкладки), либо моделируются в виде соответствующих граничных условий.
Дополнительной особенностью моделирования дентина в этой работе является введение полого канала для имитации механической работы пульпы.
Вкладка
Паз во вкладке
Цемент
Эмаль
Канал для пульпы
Дентин
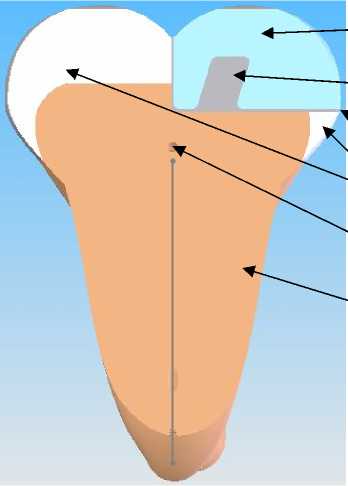
Рис. 1. Сечение зуба с пазом в установленной вкладке
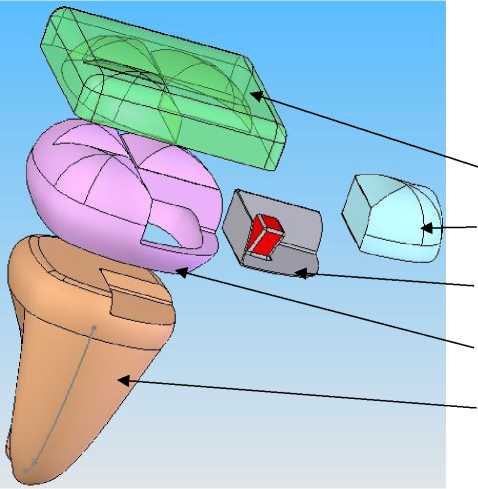
Пищевой комок
Вкладка
Цемент
Эмаль
Дентин
Рис. 2. Схема расчетной области с разнесенными деталями. Здесь указана модель с пазом во вкладке
Модель в рамках теории упругости
Все расчеты по определении и анализу напряженного состояния зуба с вкладкой (и без нее) проводятся на основе линеаризованной теории упругости. Обоснование применимости данной теории к задачам такого рода подробно обсуждается в работе [14]. Ниже приводятся ее основные соотношения в классической постановке.
Пусть исследуемое тело занимает ограниченную область Ω трехмерного евклидова пространства E 3. Замыкание области обозначим через Й , границу (которая считается достаточно гладкой) - через Г ( й = й и Г ).
-
1) Уравнение статического равновесия внутри области
Div 5 + Q = 0, x еЙ , (1)
где 5 - симметричный тензор напряжений, Q - вектор объемной силы, Q е ( С ( Й ))3. В формуле (1) и далее величины 5 , ~ , й считаются функциями координат, представленными радиусом-вектором r ей .
-
2) Деформации будем считать малыми и аддитивными, т.е. тензор малой деформации ~ представляется в виде суммы тензоров упругой ~ e и температурной s T деформации
~ = ~ e + ~ T , r ей . (2)
-
3) Упругие деформации связаны с напряжениями законом Гука
5 = С •• ~ e , r еЙ , (3)
~ где С - четырехвалентный тензор модулей упругости, СуЫ е С 1(Й).
-
4) Соотношения деформация-перемещения записываются в рамках линеаризованной теории
~ ( й) = -2(^ 7 й + й V ), r еЙ , (4)
где й - вектор перемещения, й е ( С 2( Й ))3.
Заметим, что компоненты тензора деформации удовлетворяют условиям совместности деформаций, которые эквивалентны обращению в нуль компонент тензора второго ранга rot ( rot ~) (при условии существования вторых производных от компонент деформации по координатам):
rot(rot ~) = 0, г е Й .(5)
-
5) Будем считать, что граница области Г делится на две взаимно непересекающиеся части Γ = Γ u + Γσ . На части границы Γ u заданы кинематические граничные условия, на части Г5 задан вектор напряжений P е ( С ( Г5 ))3:
й = 0, r еГй,(6)
Я•S=P, r еГ5.(7)
-
6) Будем считать, что температурные деформации ~ T е ( С 1 ( Й ))6 будут равны
T
~T =JaT(T)dT , r еЙ,(8)
t 0
где а т (T ) - тензор коэффициентов линейного теплового расширения как функция температуры T ; T g - температура, при которой тело находится в естественном (ненапряженном и недеформированном) состоянии.
Граничные условия
Прежде чем перейти к описанию граничных условий задачи, необходимо отметить предположение, которое, строго говоря, к ним не относится. При расчете напряженно-деформированного состояния авторы предлагают пренебрегать воздействием объемных сил на компоненты модели: Q = 0. Обоснование данного предположения базируется на следующих аргументах. Среди возможных источников сил Q можно указать лишь силу тяжести, порядок величины которой составляет 10 гр ∙ 9,8 м/с2 ~ 0,098 Н. Данное значение несоизмеримо мало по сравнению с нагрузками, прикладываемыми к модели.
В механических задачах вообще и, особенно, в задачах биомеханики важной частью проведения расчетов в соответствии с выбранной моделью является конкретизация граничных условий, которые необходимы для того, чтобы передать на исследуемое тело силовую или температурную нагрузку.
Традиционно выбор граничных условий в задачах биомеханики требует анализа и предположений, поскольку приходится вычленять интересующую область из более общей биомеханической системы, обладающей в целом сложной геометрией и нетривиальным движением. В этих условиях не всегда возможно заранее, не решая задачи, определить точки (области) с известными перемещением или напряжением. Зачастую этот вопрос исследователи решают интуитивно или на основании эксперимента.
Одним из принципиальных решений данной проблемы является отдаление границ от рассматриваемой области. Тогда согласно принципу Сен-Венана способ задания граничного условия будет в меньшей степени влиять на результат в интересующей исследователя области.
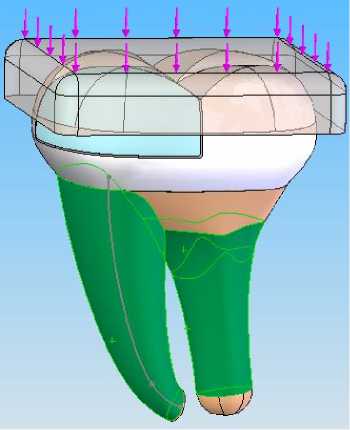
Рис. 3. Закрепленные области (отмечены темным тоном) и жевательные нагрузки
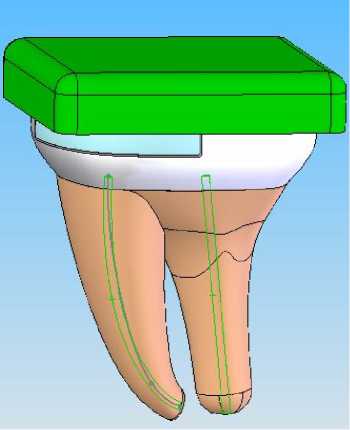
Рис. 4. Темным тоном обозначены области приложения температурных нагрузок: сверху -нагрев от жидкости температурой 60?С, снизу -каналы пульпы с температурой 36,6?С
В данной работе авторы предлагают во всех моделях считать неподвижными наружные поверхности корней зуба. Температура считается постоянной и равной 36,6?С по каналу пульпы в массе дентина, рис. 3, 4.
В отношении моделирования нагрузки на коронку зуба авторы предлагают новую идею. Дело в том, что в моделях прежних исследователей нагрузки прикладывались непосредственно к коронке, то есть делались малообоснованные гипотезы от том, каким образом та или иная сила жевания распределяется по жевательной поверхности. Поэтому в данной работе предлагается ввести в рассмотрение идеализированный фрагмент пищи или употребляемой пациентом жидкости, на который и действует необходимая нагрузка, см. рис. 4.
Другой важной особенностью является постановка в соответствии друг другу силовых и температурных граничных условий, поскольку стоит задача сравнения их влияния на зуб. Конечно, приуменьшив одно воздействие и преувеличив другое, можно добиться практически любых результатов. Ведь сравниваемое температурное воздействие никак не может быть связано с предполагаемым усилием жевания. Поэтому авторы предположительно выбрали жевательное усилие, равное 200 Н на рассматриваемый зуб, и температуру 60?С. Эти данные представлены как усредненные. Но в этом случае, как показали результаты, заметно отличие температурного и силового воздействий.
Свойства
Проблема определения свойств для элементов биомеханической конструкции в данном случае возникает не из-за того, что нет соответствующих данных. Как раз наоборот, они очень разнообразны. Так, к примеру, различные марки цемента имеют существенные отличия по физико-механическим свойствам. То же самое можно сказать и про цирконий, используемый как достаточно новый для стоматологии материал.
Проблема другого рода возникает при попытке зафиксировать температурные и упругие свойства пищевого комка.
Однако авторы видят выход из возникшей неопределенности в следующем. Основным инструментом анализа данной работы является сравнение различных вариантов геометрии и нагрузки. Поэтому достаточно выбрать некоторые усредненные характеристики для любого фрагмента модели, близкие к возможным реальным значениям. Все они сведены в следующей таблице.
Таблица
Механические свойства материалов, используемых в модели
|
Материал |
Модуль упругости, ГПа |
Предел прочности на растяжение, МПа |
Предел прочности на сжатие, МПа |
Коеффициент теплопроводности, 10-6 м2/с |
Коэффициент линейного температурного расширения, 10-6/?С |
|
Цирконий |
99 |
30 |
350 |
150,0 |
11,0 |
|
Эмаль |
48 |
21 |
270 |
0,47 |
12,0 |
|
Дентин |
18 |
36 |
260 |
0,18 |
7,5 |
|
Цемент |
23 |
– |
110 |
0,60 |
7,5 |
Результаты
Описанная выше расчетная схема со всеми указанными значениями материальных свойств и вариантов граничных условий была смоделирована численно с помощью метода конечных элементов как пространственная структура. И ниже авторы представляют иллюстрации с полученными данными, сопровождая их необходимыми комментариями.
Для иллюстрации и оценки результатов могут использоваться различные параметры напряженно-деформированного состояния. Авторы выбрали первый инвариант тензора напряжений:
o = o1 + o2 + o3,(9)
напряжения по Мизесу
0VOM = 2 ((o1 -O2 )2 +(o2 -O3 )2 +(o3 -O2 )2 F и максимальное нормальное напряжение o n =o1, где o1, o2, o3 - главные напряжения.
Здоровый зуб
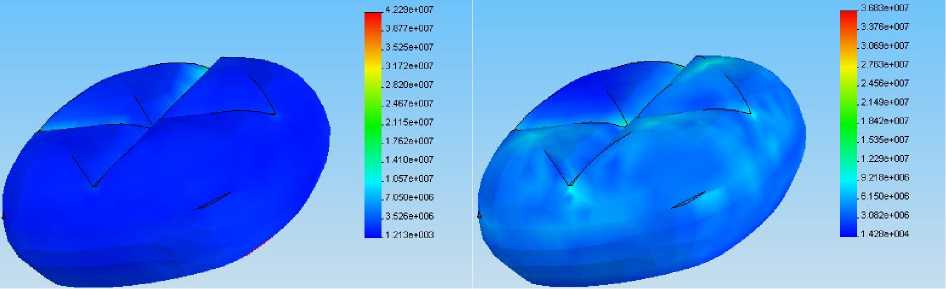
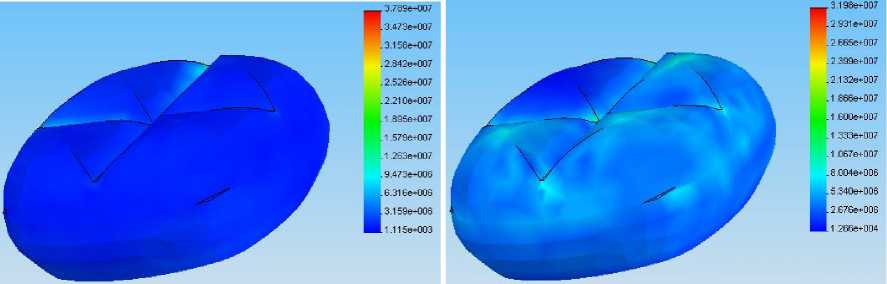
Для того, чтобы оценить эффект, создаваемый в зубе со вкладкой, температурным или силовым воздействием, авторы сначала рассматривают полноценный здоровый зуб, имеющий целые эмаль и дентин. На рис. 5–7 показаны распределения на поверхности первого инварианта тензора напряжений, напряжения по Мизесу и запаса прочности в соответствии с максимальным нормальным напряжением.
Очевидно, распределение первого инварианта тензора напряжений, напряжения по Мизесу, максимальных нормальных усилий (а также иных факторов, здесь не указанных) при температурной нагрузке менее благоприятно, поскольку большие значения в случае силовой нагрузки вызваны лишь краевыми эффектами. Можно отметить, насколько ниже запас прочности по критерию максимального нормального напряжения в случае температурного нагружения.
o , Па o , Па
Силовое нагружение Температурное нагружение
Рис. 5. Первый инвариант тензора напряжений o
σ VOM , Па
σ VOM , Па
Силовое нагружение Температурное нагружение
Рис. 6. Напряжение по Мизесу σ VOM
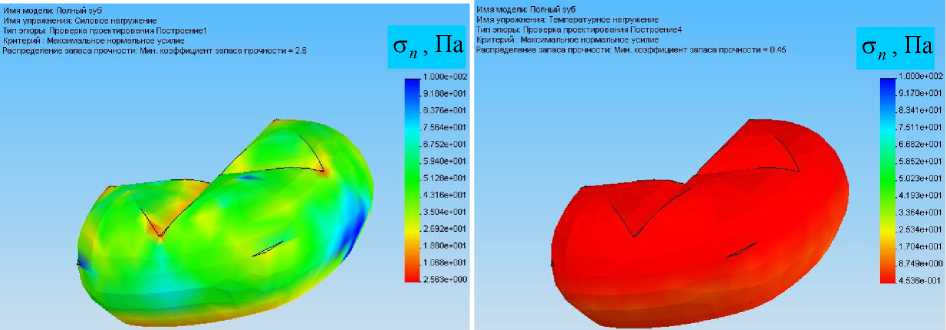
Силовое нагружение
Температурное нагружение
Рис. 7. Оценка запаса прочности по σ n
Восстановленный зуб
Теперь рассматривается зуб с установленной в него вкладкой из циркония. Причем расчеты производятся для двух вариантов формы вкладки. В первом случае вкладка имеет форму замещаемой области. Тогда слой цемента между вкладкой и тканями зуба имеет форму, показанную на рис. 8а. Во втором случае во вкладке дополнительно создается полость, заполняемая при восстановлении зуба цементом. Такой технологический прием приводит к созданию объема цемента, имеющего форму, как на рис. 8б. Для того, чтобы лучше сориентироваться, читатель отсылается к рис. 1 и 2, где область цемента из рис. 8б показана в общей композиции. На рис. 9 показана расчетная область дентина и эмали для обоих типов вкладки. Видно, что при выполнении операции врачу приходится препарировать как эмаль, так и дентин в относительно больших объемах.
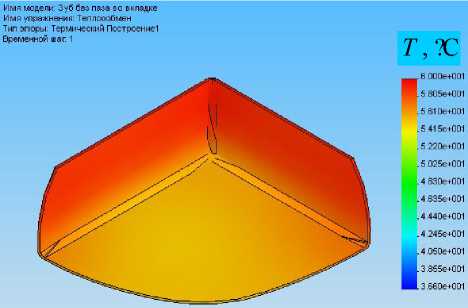
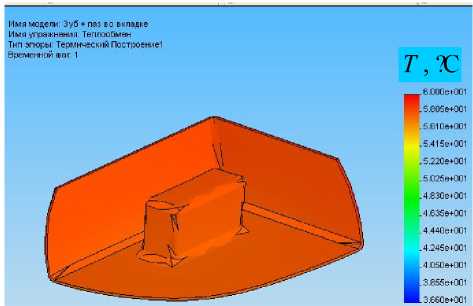
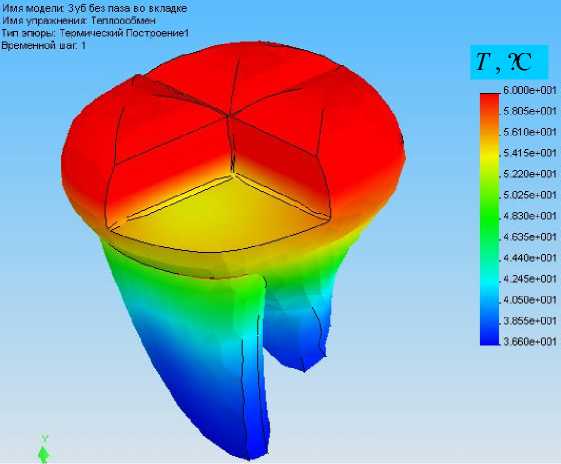
Дальнейшие решения искались для двух задач на одной и той же модели области: задачи теплопроводности и задачи термоупругости при сформулированных граничных условиях. Так, на рис. 10 проиллюстрировано, как распределяется температура по объему цемента при квазистатическом температурном нагружении для обоих форм вкладки. Следует отметить, что в случае использования дополнительного паза температура распределяется ровнее. На диаграмме (рис. 10б) визуально вообще невозможно выделить области с температурой, отличной от средней по объему цемента. В отношении же остальных элементов модели (рис. 11) эффект от применения паза при решении задачи теплопроводности вообще не заметен.
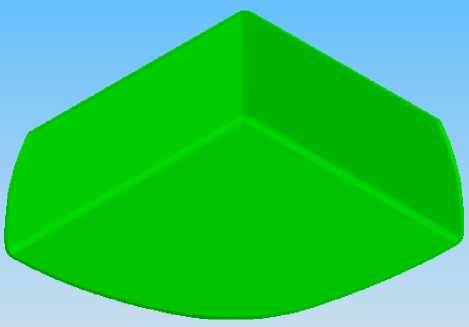
Рис. 8. Форма цемента для рассматриваемых случаев подготавливаемой формы вкладки

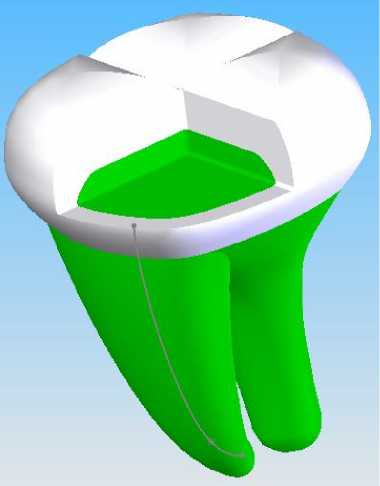
Рис. 9. Схема подготовки полости для установки вкладки с цементом в виде прослойки
а
б
Рис. 10. Распределение температуры по объему цемента для вкладки без паза (а) и с пазом (б)
а
б
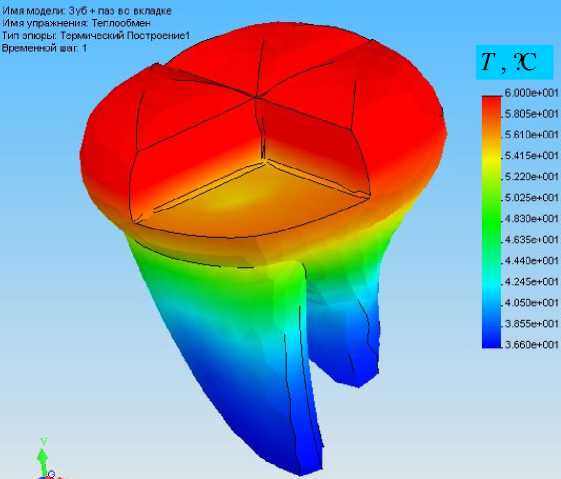
Рис. 11. Распределение температуры по объему сохранившихся тканей зуба (рис. 9) при применении вкладки без паза (а) и с пазом (б)
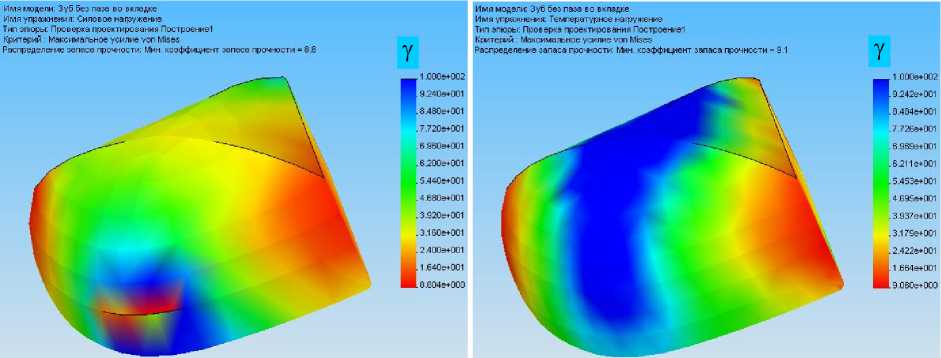
а б
Рис. 12. Оценка запаса прочности по нормальному напряжению для вкладки без паза при силовом (а) и температурном (б) нагружениях

а б
Рис. 13. Оценка запаса прочности по максимальному касательному усилию для вкладки без паза при силовом (а) и температурном (б) нагружениях
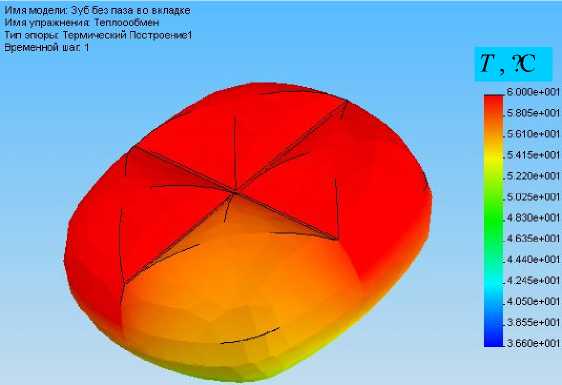
Рис. 14. Распределение температуры по объему цемента для вкладки без паза
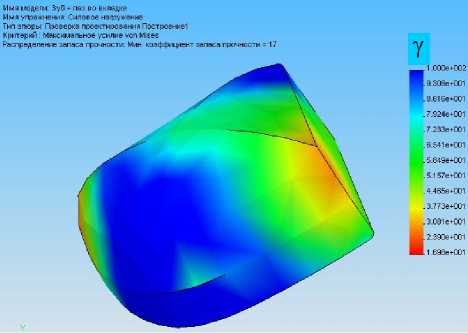
а
б
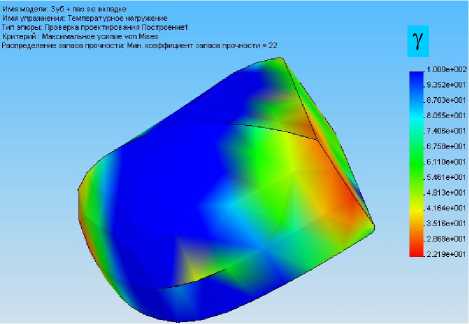
Рис. 15. Оценка запаса прочности по нормальному напряжению для вкладки с пазом при силовом (а) и температурном (б) нагружениях

а
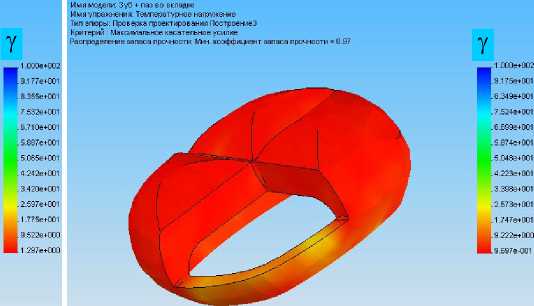
б
Рис. 16. Оценка запаса прочности по максимальному касательному усилию для вкладки с пазом
при силовом (а) и температурном (б) нагружениях
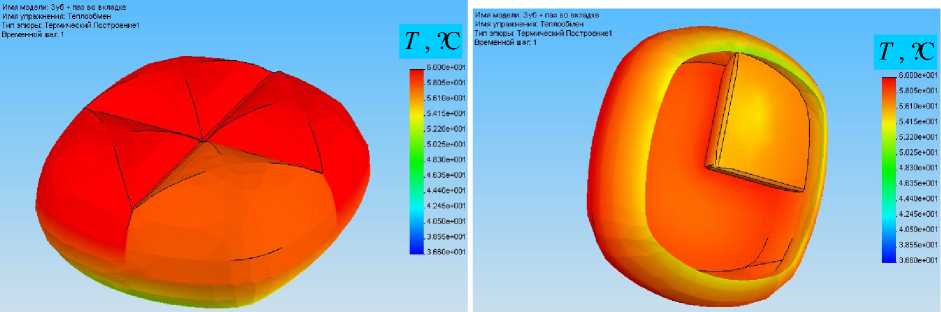
Рис. 17. Распределение температуры по объему цемента для вкладки без паза: а – вид снаружи, б
– вид изнутри без дентина
Рассмотрим теперь отдельно параметры напряженно-деформированного состояния вкладки без паза и с пазом и сравним ее работу при силовом и температурном нагружениях. Результаты представлены на рис. 12–17.
Выводы
На основании проделанных расчетов и полученных числовых значений можно со всей определенностью сделать следующие выводы.
-
1. Критерий максимального нормального напряжения дает результат, при котором эмаль зуба должна начать разрушаться уже при употреблении напитков или пищи с температурой около 60?С. Однако этого не происходит, и объяснение этому авторы видят в том, что такой критерий плохо применим для таких существенно неизотропных материалов, как эмаль.
-
2. В данной работе предложено новое решение проблемы приложения нагрузки к зубу с использованием пищевого комка. Такой подход избавил авторов от необходимости определять форму и распределение усилий по поверхности эмали и вкладки зуба. Авторы считают, что данная идея может быть применена и при анализе иных биомеханических конструкций, позволяя решить нетривиальную проблему задания граничных условий.
-
3. Еще одним значимым отличием работы от известных ранее стало использование температурной нагрузки в качестве основного воздействия на зуб. С помощью
-
4. Применение паза во вкладке приводит к улучшению теплообмена и снижению напряжений в сильно нагруженных областях на величины порядка 10%. Такой вывод можно сделать на основании численных результатов, проиллюстрированных на рис. 11–17.
расчетов было показано, что температурное воздействие на зуб приводит к более негативным последствиям, нежели силовое нагружение.


