Конечно-элементный анализ концевых фрез для учета упругих отжатий при выборе режимов резания в точном приборо- и машиностроении

Современное приборо- и машиностроение характеризуется повышенными требованиями к точности механической обработки. За последние 10 лет уровень требуемых параметров точности при механообработке повысился примерно на один порядок. Например, в приборостроении при обработке внутренних элементов (карманов) требуется получить 10–12 квалитет точности. Это соответствует допускам менее 0,05 мм.

В процессе механообработки на станках с ЧПУ на режущий инструмент действует распределенная нагрузка. В случае с концевыми фрезами эта распределенная нагрузка действует на некоторой длине, которая называется шириной фрезерования, и вызывает отжатия инструмента. Вследствие таких деформаций (упругих отжатий) возможны неточности в обработке стенок, что приводит к производственному браку. Для устранения данной проблемы была поставлена задача исследовать упругие отжатия концевых фрез методом конечных элементов. Величина этих отжатий будет учитываться при выборе режимов резания.

В задаче использовалась модель концевой фрезы, соответствующая ГОСТ 23247-78 «Фрезы концевые для обработки деталей из легких сплавов на станках с программным управлением. Конструкции». Для изготовления концевых фрез используется быстрорежущая сталь марки Р6М5. Эта сталь пригодна для обработки легированных конструкционных сталей и титановых сплавов. Допускаемые напряжения на изгиб этой быстрорежущей стали составляют 0,34 ⋅ 10¹⁰ Па [1].

Задача упругого поведения относится к классу конструкционных задач, решение которых производится с помощью программного комплекса ANSYS. ANSYS – комплекс связанных программ для конечно-элементного анализа инженерных систем, позволяющий решать междисциплинарные задачи, в том числе задачи упругости в условиях статического и динамического нагружения конструкции.

Исходная геометрическая модель концевой фрезы была построена в CAD-системе SolidWorks, после этого она была импортирована в формате Parasolid в систему ANSYS, где была построена смешанная конечно-элементная сетка. Модели представлены на рис. 1 а, б.

Рис. 1, а. Геометрическая модель концевой фрезы

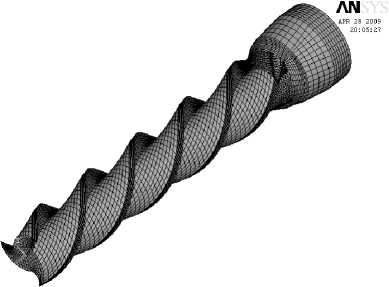
Рис. 1, б. Смешанная конечно-элементная модель концевой фрезы

Для приложения вектора продольной составляющей силы резания был смоделирован участок заготовки в зоне резания таким образом, что его обрабатываемая поверхность представляет собой след от зацепления (врезания) с зубьями фрезы (рис. 2, а). На рис. 2, б показана область зацепления в разрезе; в разрезе (рис. 3, а) показана конечно-элементная модель с областью зацепления.

Продольная составляющая силы резания вычисляется из эмпирического выражения [2]:

P y = ( 0,6 * 0,8 ) - 10 • C p • t x • S^y • B u • z • D- q • k ; ¹. (1) Здесь (для концевой фрезы диаметром 12 мм) t - глубина резания ( t = 2 мм); S - подача ( S = 0,06 мм/зуб); B - ширина фрезерования ( B = 15 мм); z - число зубьев, участвующих в зацеплении ( z = 2); D - диаметр фрезы ( D = 12 мм); x , y , u , q - эмпирические показатели степени [2]; K_m , C p - табличные коэффициенты [2]. Величина продольной составляющей силы резания составила 463 Н.

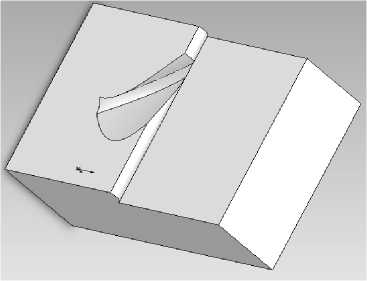
с концевой фрезой

Рис. 2, б. Область зацепления (разрез)

Рис. 2, а. Поверхность со следом зацепления

Граничные условия для фрезы - жесткая заделка на хвостовике.

Участок заготовки имеет высоту, равную ширине фрезерования, и ограничен по следующим степеням свободы: повороты вокруг всех осей, перемещения вдоль осей X и Z . Со стороны заготовки на режущую кромку фрезы действует сила P_y , которая передается через контактные конечные элементы в виде распределенной нагрузки на заданную ширину фрезерования.

Расчетная модель показана на рис. 3, б.

На рис. 4, а показаны упругие отжатия концевой фрезы диаметром 12 мм. Отжатия происходят по осям X и Y и превышают 0,1 диаметра. В результате таких отжатий обрабатываемая стенка не получится вертикальной, во многих случаях это не удовлетворяет точности механической обработки.

Технология

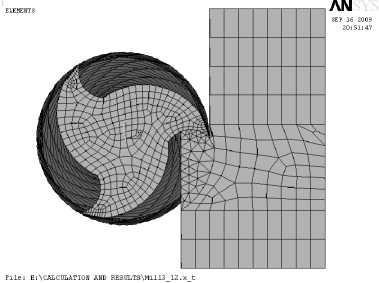
Рис. 3, а. Конечно-элементная модель взаимодействия фрезы и заготовки

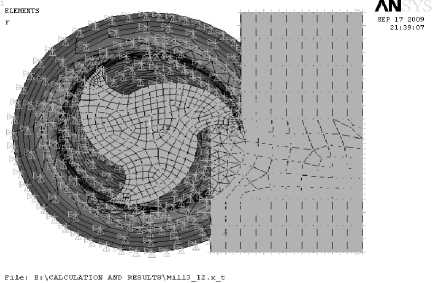
Рис. 3, б. Модель с граничными условиями

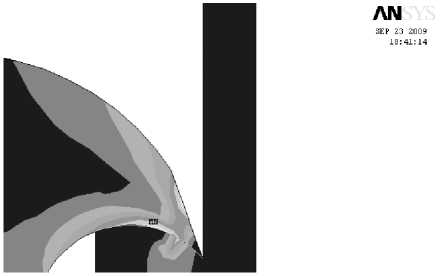
Рис. 4, а. Упругие отжатия

Рис. 4, б. Эквивалентные напряжения по Мизесу (разрез)

На рис. 4, б показаны эквивалентные напряжения по Мизесу (расчетный параметр SEQV), вычисленные в узлах (Nodal solution). Напряжения усреднены по элементам, окружающим каждый расчетный узел. Зона наибольших напряжений расположена в области зацепления зубьев фрезы с заготовкой и не превышает допустимых напряжений изгиба.

Конечно-элементный анализ показал, что у некоторых фрез необходимо изменять режимы резания из-за больших величин упругих отжатий f _фр . Для этого нами вводится новый параметр:

коэффициент податливости – K _ω , который определяется выражением:

K ^f ид.ст    ^ω ид.ст

.

ω ^{== f} фр ^ω фр

Здесь ω ид.ст и ω фр ( f ид.ст и f фр ) – податливость (упругие отжатия) идеального стержня и фрезы равных диаметров соответственно. Поскольку величина податливости связана с величиной упругих отжатий f и с составляющей силы резания P_y [3], то выражение для вычисления коэффициента податливости будет иметь следующий вид:

P ⋅ω

_{K ω =} y ид.ст .                                                                                           (3)

^f фр

После некоторых математических преобразований получаем следующее уравнение, отображающее связь между режимами резания и величиной упругих отжатий:

0,8 ⋅ 10 ⋅ C_p ⋅ t^x ⋅ S^y ⋅ B^u ⋅ z ⋅ D ^{- q} ⋅ K_m ^{- 1} = ^{f фр} K _ω .                                                     (4)

p ид.ст

Как видно, левая часть представляет режимы резания. В правой части: f _фр – вычисляемая величина упругих отжатий; K _ω – коэффициент податливости. K _ω выбирается из результатов конечно-элементного анализа для конкретного типа фрезы заданного диаметра, продольных размеров и величины податливости идеального стержня ω ид.ст , рассчитанной с учетом той нагрузки, которая действует на реальную фрезу того же диаметра.

Уравнение (4) может быть использовано в работе технолога-программиста. Выбирая по технологическим справочникам режимы резания, коэффициент податливости и рассчитывая величину податливости идеального стержня по известным зависимостям сопротивления материалов, технолог-программист вычисляет величину упругих отжатий. Если величина упругих отжатий не превышает допустимой, то выбранные режимы являются приемлемыми, если условие не выполняется, то поступить можно двумя основными способами:

• 1)    уменьшить подачу S ;

• 2)    уменьшить ширину фрезерования B .

Вывод: данная методика применима, если рассматривать силовое фрезерование, т. е. такой вид обработки, где ширина фрезерования превышает величину диаметра. Методика не распространяется на скоростное фрезерование, поскольку ширина фрезерования там имеет малую величину (материал снимается мелкими слоями) и податливость не влияет на погрешность обработки.