Конечно-элементный анализ процесса формообразования крутоизогнутых деталей из труб методом проталкивания

моделирования крупных вихрей (Large Eddy Simulation, LES) [3, 4, 5]. Метод RANS основан на тотальном осреднении всего спектра турбулентных пульсаций и его представлении в виде характеристик турбулентности, таких как, кинетическая энергия турбулентности и скорость её диссипации. Его преимуществами являются относительно невысокие требования к пространственной дискретизации и параметрам вычислительной техники. Недостатками – отсутствие возможности моделирования вихревых структур с размерами порядка макромасштаба потока, наличие эмпирических коэффициентов при замыкании уравнений и, как следствие, отсутствие приемлемой универсальности. Метод крупных вихрей основан на математическом разделении потока на крупновихревое и мелковихревое движение с помощью процедуры фильтрации. Влияние мелковихревого движения описывается приближенными, так называемыми подсеточными моделями. В качестве фильтра в основном выступает локальный размер конечно-элементной сетки. Преимуществами метода крупных вихрей являются возможность получения параметров среднего течения, а также спектральных характеристик, пространственных и временных масштабов турбулентности. Недостатком подхода LES являются более высокие требования к вычислительной технике.

Целью данной работы является сравнение методов моделирования турбулентности на основе решения осредненных по Рейнольдсу уравнений Навье-Стокса в нестационарной постановке (Unsteady Reynolds Average Navier-Stokes, URANS)

и метода моделирования крупных вихрей (Large Eddy Simulation, LES) при исследовании течения за уголковым стабилизатором пламени.

В качестве предмета исследования выбрано плохообтекаемое тело в виде правильной треугольной призмы с длиной ребра основания h = 25 мм, установленное в канале квадратного сечения 50х50 мм. Скорость набегающего потока равна 10 м/с, профиль скорости – равномерный. Интенсивность турбулентности на входе – 2%. Схема экспериментального участка представлена на рис. 1. Исходные данные и результаты экспериментальных измерений взяты из статьи [6]. В расчёте длина канала до стабилизатора принята равной 4h и вниз по потоку от стабилизатора 10h.

Расчёт проводился в трехмерной нестационарной постановке в программном комплексе ANSYS Fluent 14.5. Для создания блочно-структурированной конечно-элементной сетки геометрическая модель расчётной области была разделена на 7 блоков (рис. 2).

На первом этапе проводился расчёт изотермического течения воздух. При расчёте в постановке URANS использовались следующие модели турбулентности, реализованные в ANSYS Fluent: k-e Standard, k-e Realizable, k- m SST,

Reynolds Stress Model (RSM). При использовании URANS необходимо исследовать зависимость решения от плотности дискретизации расчётной области и размера временного шага [7]. Для этого проводятся расчёты на нескольких вариантах сеток с последовательным увеличением плотности в 2 и более раз. В нашем случае расчёт проводился для трех различных вариантов сеток, количество конечных элементов в которых равнялось 0,70 млн., 1,43 млн. и 3,69 млн. штук. Для определения зависимости решения от шага по времени использовались различные значения временных шагов: 5 мс, 1 мс, 0,1 мс.

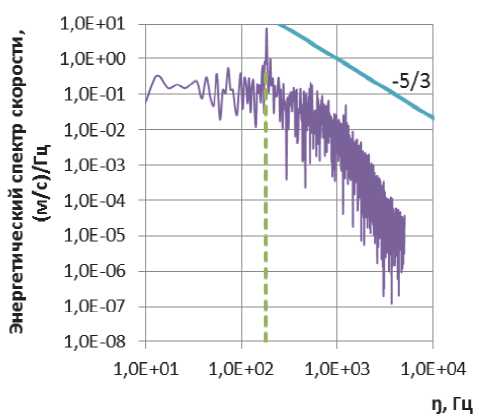
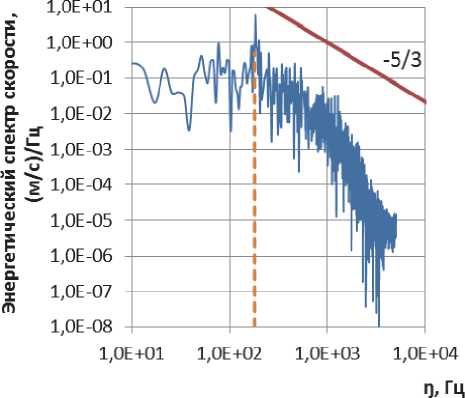
Расчёт в постановке LES проводился на сетке 3,69 млн. с шагом по времени 0,1 мс. Исходя из формулировки подхода LES, необходимо, чтобы размер конечно элементной сетки позволял разрешить самые крупные вихревые структуры, находящиеся вне инерционного интервала спектра кинетической энергии турбулентности (рис. 3) [4]. Для развитого турбулентного течения этот участок описывается законом Колмогорова-Обухова (закон «5/3») [5]:

, где – энергетический спектр, =1,5 – постоян-

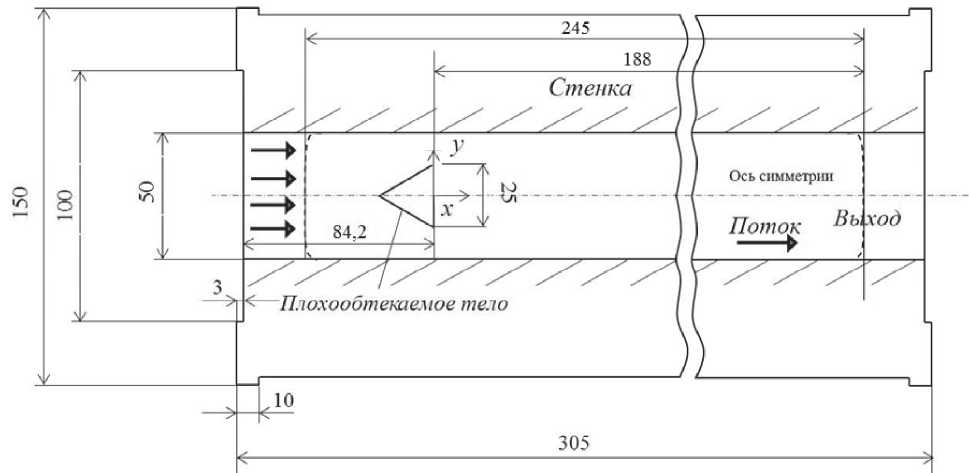
Рис. 1. Схема экспериментального участка [6]

Рис. 2. Геометрическая модель расчётной области

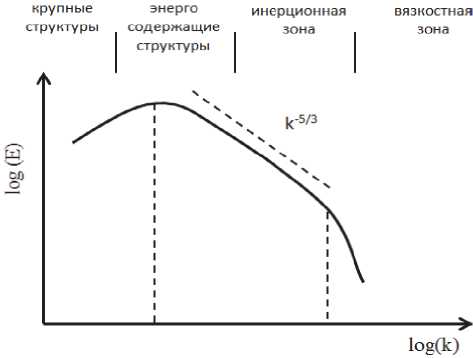
Рис. 3. Спектр турбулентной кинетической энергии ная Колмогорова, к – кинетическая энергия турбулентности, £ – скорость диссипации кинетической энергии турбулентности.

На рис. 4 представлены результаты преобразования Фурье абсолютной скорости поток, по- лученной в результате расчёта изотермического течения с использованием динамической подсеточной модели Smagorinsky-Lilly. Изменение скорости во времени записывалось для трех точек со следующими координатами: №1 У] =0,5h, X,=1h; №2 Уз =0,5h, Хя=2h; №3 Уз =0,5h, хэ=3h. Из графиков видно, что для всех точек имеется участок, соответствующий закону «5/3» Колмогорова-Обухова. Также обнаружен ярко выраженный пик на частоте 170-190 Гц, что соответствует экспериментальным данным [6].

Для выбора подхода подсеточного моделирования при использовании LES были проведены расчёты с использованием следующих моделей: динамическая модель Smagorinsky-Lilly (SL), Wall-Adapted-Local-Eddy (WALE) и Wall-Modeled (WM) [3, 4]. На рисунке 5 представлены графики изменения осевой скорости Vx вдоль центральной линии модели (ось x) и расхода воздуха в зоне обратных токов вдоль её длины, где G_ЗОТ - расход через зону обратных токов (ЗОТ),

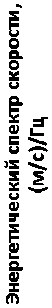
I), Гц

а)

в)

Рис. 4. Результаты быстрого преобразования Фурье для скорости в трех точках а) – точка №1, б) – точка №2, в) – точка №3

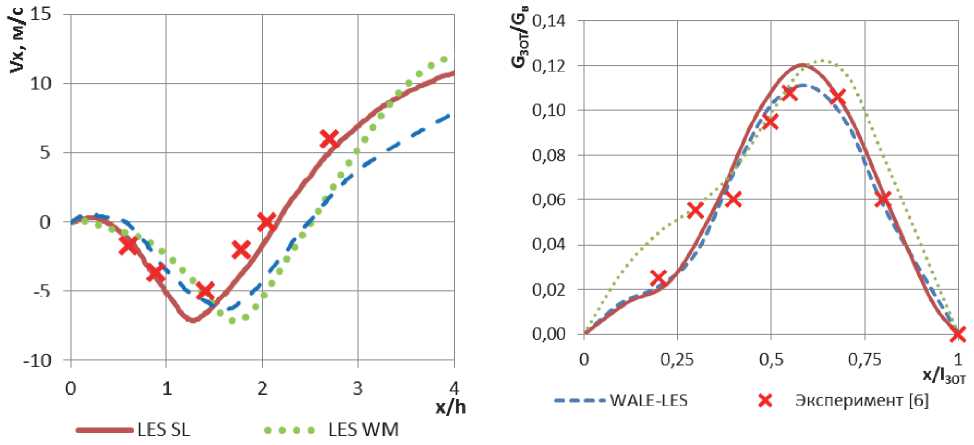
Рис. 5. Осевая скорость потока вдоль центральной линии (а) и расход воздуха в зоне обратных токов (б)

G_В – расход воздуха на входе в расчётную область, l_ЗОТ – протяженность ЗОТ.

Из графика видно, что все используемые модели дают похожие результаты, и адекватно отражают осредненные по времени характеристики потока. Однако, наиболее близкие результаты к экспериментальными данным показала динамическая модель Smagorinsky-Lilly, которая и была выбрана для дальнейших расчётов и сравнения с URANS.

Одним из определяющих параметров для устройств стабилизации пламени является размер зоны обратных токов [1, 8]. Полученные размеры ЗОТ в осевом направлении для всех вариантов конечно-элементных сеток, временных шагов и моделей турбулентности представлены в табл. 1. Значения указаны в калибрах относительно длины ребра стабилизатора. Экспериментальное значение равнялось 2,1h [6]. На рис. 6 представлены поля мгновенной скорости потока при расчёте с использованием подхода URANS и LES.

Из результатов видно, что при расчёте изотермических течений подход URANS не позволяет получить крупновихревого нестационарного течения, наблюдаемого в эксперименте. Протяженность зоны обратных токов при этом в 1,7 и более раз больше, чем при натурных исследованиях. Полученные данные согласуются с результатами, представленными в работах [3, 13, 14]. При расчёте с использованием LES размер ЗОТ отличается от эксперимента не более чем на 5%, даже на самой крупной сетке.

На следующем этапе проводилось исследование горения заранее подготовленной пропановоздушной смеси. Расчёт процесса горения газообразного топлива описывался с использовани-

Таблица 1. Протяженность ЗОТ при расчёте на различных моделях турбулентности

	Модель турбулентности		Протяженность ЗОТ, h
			5мс	1мс	0,1мс
Сетка №1 0,70 млн.	co I	k-e STN	3,62	3,65	3,55
		k-e Real	4,10	4,18	4,16
		k-w SST	4,51	4,52	4,51
		RSM	4,89	4,87	4,89
	LES	SL	-	-	2,08
Сетка №2 1,43 млн.	co i	k-e STN	3,63	3,59	3,63
		k-e Real	4,14	4,12	4,12
		k-w SST	4,52	4,52	4,52
		RSM	5,42	4,90	4,01
	LES	SL	-	-	2,15
Сетка №3 3,69 млн.	co i	k-e STN	3,78	3,63	3,67
		k-e Real	4,08	4,12	4,10
		k-w SST	4,55	4,53	4,54
		RSM	5,20	5,19	4,90
	LES	SL	-	-	2,13

а)

б)

Рис. 6. Поля мгновенных скоростей потока: а – URANS RSM, б – LES SL

ем модели конечной скорости химической реакции, которая предполагает расчёт скоростей реакций по уравнению Аррениуса. В данной работе использовались два механизма: глобальная реакция окисления пропана и редуцированный кинетический механизм, предложенный в работе [9], который содержит 17 компонентов и 28 реакций. Для определения границы бедного срыва пламени использовался следующий алгоритм. В начале, проводился расчёт течения изотермической заранее подготовленной смеси с б=1. Затем, за стабилизатором пламени локально увеличивалась температура потока выше необходимой для воспламенения (1500 К). Далее проводился расчёт до достижения устойчивого, периодически повторяющегося решения. Условием этого было повторяемость результатов за два последовательных промежутка времени, равных 3 , где - характерное время пребывания. Согласно рекомендации [10] характерное время определяется как:

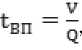
где V – объем расчётной области, Q – объемный расход на входе.

Результаты сравнивались по полю осреднён-ной по времени температуры и полю её среднеквадратичного отклонения. Расчёт продолжался , затем на входе в расчётную область ступенчато увеличивался коэффициент избытка воздуха с шагом         . Для определения момента срыва пламени на каждом временном шаге записывалась среднемассовая температура потока в трех сечениях: на расстоянии x=2h, x=5h и на выходе из расчётной области.

Изменение температуры во времени в сечении 2h при расчёте с использованием глобальной реакции представлено на рис. 7. Из графика видно, что бедный срыв пламени происходит при =2,5-2,6, экспериментальное значение =1,9 [6]. Это свидетельствует о том, что модель горения, основанная на глобальной реакции, завышает реакционную способность бедных смесей.

Изменение температуры во времени в трёх сечениях при расчёте с использованием кинетического механизма, предложенного в работе [9] представлено на рисунке 8. В этом случае погасание пламени в сечении x=2h происходит при

=1,6. Падение температуры в сечениях, которые находятся вниз по потоку, происходит с неболь-

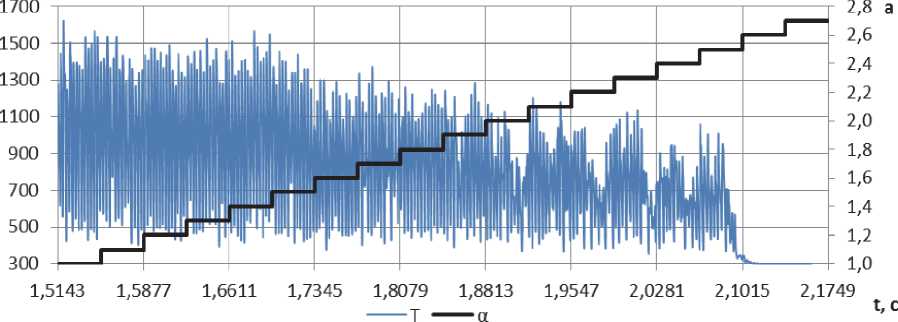
Рис. 7. Температура в сечении x=2h при расчёте с использованием 1 реакции

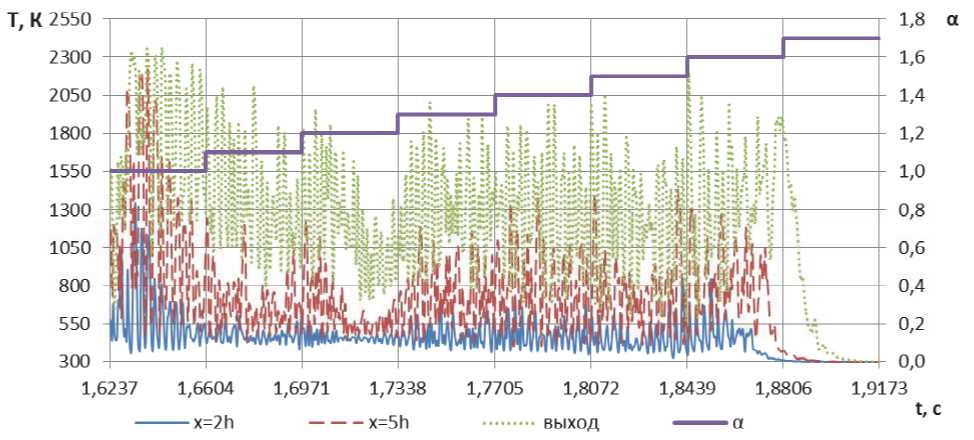
Рис. 8. Изменение температуры при расчёте с использованием редуцированной кинетической схемы [9]

шим запаздыванием. Однако, данное значение ниже, чем экспериментальное. Возможно, это связано с недостаточным пространственным разрешением, в результате чего поверхность фронта ламинарного пламени оказалось меньше, чем в реальности, как следствие занижена турбулентная скорость распространения пламени. Решением может быть использование моделей горения утолщенного фронта пламени [11], для которых при расчёте толщины фронта пламени и скорости его распространения учитывается сеточное разрешение или использование специальных процедур подсеточного моделирования [12].

Также обнаружено, что на предсрывном режиме стабилизация пламени определяется поведением крупных вихревых структур: их временем пребывания в ближнем следе за стабилизатором, частотой схода с кромок и взаимодействием между собой.

В результате можно сказать, что при использовании подхода URANS для моделирования течений с крупными трехмерными вихревыми структурами не удалось получить нестационар- ной картины течения, протяженность ЗОТ завышена по сравнению с экспериментом в 1,7 и более раз. Более перспективным для данного типа течений является подход моделирования крупных вихрей. Данный подход показал удовлетворительное согласование с экспериментом по протяженности ЗОТ, распределению скорости вдоль центральной линии и расходу воздуха через ЗОТ. Также показана принципиальная возможность исследования явления бедного срыва пламени при заданном законе изменения б как функции от времени. Выявлено, что существенное влияние на результаты расчёта оказывает используемый кинетический механизм химических реакций. Для более точного описания поведения пламени необходимо использовать расширенные механизмы химических реакций и апробированные модели турбулентнохимического взаимодействия.