Конечные непримарные группы, все собственные фактор-группы которых примарны

Теорема. Пусть G - конечная непри-марная группа, всякая собственная факторгруппа которой является примарной группой. Тогда G принадлежит одному и только одному из следующих классов групп:

• I.    G = A х B, где |A| = p, |b| = q.

• II.    G = A • B , где A - элементарная абелева p -группа, являющаяся минимальным нормальным делителем; B – q -группа, не имеющая инвариантных в G подгрупп, кроме единичной.

• III.    G = A • B , где A - произвольная неразрешимая группа, являющаяся минимальным нормальным делителем; B – p -группа, не имеющая инвариантных в G подгрупп, кроме единичной.

Доказательство

Достаточность проверяется непосредственно.

Необходимость. Пусть сначала G – абелева группа. Тогда G делится ровно на 2 различных простых числа и порядок всякой силовской подгруппы группы G – простое число. Таким образом, G – группа типа I теоремы.

Пусть G – разрешимая неабелева группа и A – абелев неединичный член ряда коммутантов группы G . Так как всякая факторгруппа группы G является примарной группой, то A – силовская p -подгруппа и A не имеет собственных подгрупп, инвариантных в G . Отсюда следует, что A – минимальный нормальный делитель, являющийся элементарной абелевой p -группой.

Фактор-группа

G A

является q -группой

частности, разрешимой группой, а группа G –

B , причем ясно, что в B нет подгрупп, инвариантных в G , кроме единичной. Таким образом, G – группа типа II теоремы.

Пусть G – неразрешимая группа и A – ее

неразрешимая группа, то и A – неразрешимая

группа. Фактор-группа

G A

является   p -

минимальный нормальный делитель. Так как

фактор-группа

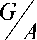
является p -группой и, в

группой B . Ясно, что B не имеет инвариантных в G подгрупп, кроме единичной. Таким образом, G – группа типа III теоремы. Необходимость доказана. Теорема доказана.

Finite nonprimary groups in which every nontrivial factor-group is primary

S. I. Faershteyn1, I. S. Faershteyn2