Конечные неразрешимые группы, графы Грюнберга - Кегеля которых изоморфны графу "балалайка". Случай q≤3

Пусть G — конечная группа. Через n(G) обозначается множество всех различных простых делителей порядка группы G, а через w(G) — множество порядков элементов из G. Графом Грюнберга — Кегеля (или графом простых чисел) r(G) конечной группы G называется граф, в котором множеством вершин является множество всех простых делителей порядка группы G и две различные вершины p и q смежны тогда и только тогда, когда в группе G существует элемент порядка pq . «Балалайка» — граф на 4 вершинах, степени которых равны 1, 2, 2 и 3.

Первый автор описал конечные группы с графом Грюнберга — Кегеля как у группы Aut(J 2 ) (см. [1]) и как у группы A 10 (см. [2]). Графы Грюнбергa — Кегеля этих групп изоморфны (как абстрактные графы) графу «балалайка».

В [3] была поставлена более общая проблема: описать конечные группы, графы Грюнберга — Кегеля которых изоморфны графу «балалайка».

В [3] А. С. Кондратьев и Н. А. Минигулов доказали, что если G — конечная неразрешимая группа и граф r(G) изоморфен графу «балалайка», то фактор-группа G/S(G) группы G по ее разрешимому радикалу S(G) почти проста, и класифицировали все конечные почти простые группы G, графы r(G) которых изоморфны подграфам графа «балалайка». В [4] А. С. Кондратьев и Н. А. Минигулов описали все конечные разрешимые группы, графы Грюнберга — Кегеля которых изоморфны графу «балалайка». Также в [5] они классифицировали конечные неразрешимые группы G, графы r(G) которых изоморфны графу «балалайка» в следующих двух случаях: (1) группа G не содержит элементов порядка 6; (2) группа G содержит элемент порядка 6 и вершина q графа r(G) делит | S(G) | .

В данной работе мы продолжаем исследование проблемы. Пусть G — конечная неразрешимая группа, граф r(G) изоморфен графу «балалайка», т. е. граф r(G) имеет вид

r

■о

s

pq

где r, s, p и q — некоторые попарно различные простые числа. Положим S = S(G) и G = G/S . Ввиду [3] группа G почти проста известного вида. Положим L = Soc(G). Предположим далее также, что S(G) = 1, G содержит элемент порядка 6 и q не делит | S | . Поскольку группа G неразрешима, имеем 2 G n(G)) и | n(G) | € { 3,4 } . Если 3 / n(G)), то ввиду [6-8] имеем G G { Sz(8), Sz(32), Aut(Sz(32)) } и, следовательно, n(G) = n(G); противоречие с тем, что 3 G n(G). Поэтому 3 G n(G)).

Мы доказываем следующую теорему.

Теорема. Пусть G — конечная неразрешимая группа, G := G/S(G), граф r(G) как абстрактный граф изоморфен графу «балалайка» с q ^ 3. Если G содержит элемент порядка 6 и q не делит | S(G) | , то p = 2, q = 3, G = A 5 или S 5 , { r, s } = {t, 5 } для некоторого простого числа t >  5 и t G n(S(G)) C { 2, 5, t } .

Замечание. Утверждение теоремы реализуется. Пусть G = Z х ((V i х V 2 ) х L), где Z = Z 2 , L = SL 2 (5), V i — любой точный 2-мерный GF(t)(/5 ^-модуль для любого простого числа t >  5 (V iL — группа Фробениуса с ядром V i и дополнением L) и V2 — естественный 2-мерный GF (5)L-модуль. Тогда граф r(G) изоморфен «балалайке», и имеет вид

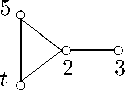
Можно доказать, что случай G = S 5 утверждения теоремы также реализуется.

• 2.    Обозначения и вспомогательные результаты

Наши обозначения и терминология в основном стандартны, их можно найти в [9–15].

Если группа G действует на группе H , то будем говорить, что неединичный элемент g G G действует на H свободно (или без неподвижных точек), если C h (д') = 1.

Рассмотрим некоторые результаты, которые используются в доказательстве наших результатов.

Следующее утверждение хорошо известно и легко доказывается.

Лемма 1. Пусть G — конечная квазипростая группа, F — поле характеристики p > 0, V — абсолютно неприводимый F G-модуль и β — характер Брауэра модуля V . Если g — элемент простого порядка, отличного от p, из G, то dimcv(g) = (e \ы, 1 \ы) = t1 £ e(x). 1 g1 xe(g)

Лемма 2 [14, теорема VII.1.16] . Пусть G — конечная группа, F = GF (pm) — поле определения характеристики p >  0 для абсолютно неприводимого FG-модуля V, (a) = Aut(F), V o обозначает модуль V , рассматриваемый как GF(p')G-модуль, и W = V o ® gf (p) F. Тогда

• (1)    W = ® m =i V ^a i , где V ^CT i — модуль, алгебраически сопряженный с V посредством a i ;

• (2)    V o является неприводимым GF(p')G-моду.лем и, в частности, W реализуется как неприводимый GF (р^-модуль V 0 ;

• (3)    с точностью до изоморфизма модулей неприводимые GF(p')G-модули находятся во взаимно однозначном соответствии с классами алгебраической сопряженности неприводимых GF(p)G-модулей.

Лемма 3 [12, теорема 5.3.11] . Пусть p — простое число и P — конечная p-группа. Тогда P обладает характеристической подгруппой C , называемой критической подгруппой в P , со следующими свойствами:

• (a)    группа C/Z(C ) элементарная абелева;

• (b)    [P,C ] С Z (C );

• (c)    C p (C) = Z(C );

• (d)    каждый нетривиальный p^r-автоморфизм группы P индуцирует на C нетривиальный автоморфизм.

Лемма 4 [5, лемма 11] . Пусть p, q и r — попарно различные простые числа и G — конечная группа вида G = P х (T х (x)), где P — нетривиальная р-группа, T — q-группа, | x | = r и C g ( P ) = Z(P). Пусть C — критическая подгруппа в T и [T, ( x ) ] = 1. Тогда либо C p (x) = 1, либо Z(T ) С Z(C ) С C t (x), q = 2, r = 1 + 2 n — простое число Ферма и [C, (x) ] — экстраспециальная группа порядка 2 ²ⁿ⁺¹ .

Лемма 5 [16, лемма 1] . Пусть G — конечная группа, N — нормальная подгруппа в G, G/N — группа Фробениуса с ядром F и циклическим дополнением C. Если (\F | , | N | ) = 1 и F не содержится в NC g ( N )/N, то s\C | G ^(G) для некоторого s G n(N).

Лемма 6 [17, предложение 3.2] . Пусть G — конечная группа, H < G, G/H = L 2 (q), где q нечетно, q > 5, и C h (t) = 1 для некоторого элемента t порядка 3 из G. Тогда H = 1.

Лемма 7 [17, предложение 4.2; 18, теорема 8.2] . Пусть G — конечная группа, 1 = H = L2(2ⁿ), где n ^ 2. Предположим, что Ch (t) = 1 для некоторого элемента t порядка 3 из G. Тогда H = 02(G) и H является прямым произведением минимальных нормальных подгрупп порядка 2²ⁿв G, каждая из которых как G/H-модуль изоморфна естественному GF(2ⁿ)SL2(2ⁿ)-модулю.

Пусть p — простое число, q = p^l, P — алгебраическое замыкание поля GF(q) n ^ 2, L = SL _n (q) — специальная линейная группа степени n ^ 2 над полем GF(q) и L = SL _n (P ). Пусть w i , ... ,w _n- i — фундаментальные веса группы L. Каждый неприводимый PL-модуль имеет старший вес w = a i w i + ... + a _n- i w _n- i для некоторых неотрицательных целых чисел a i ,..., a _n- i . Этот старший вес называется q-ограниченным, если a i < q для i = 1,..., n — 1. Ввиду известной теоремы Стейнберга [9, § 13, теорема 43] ограничение на L неприводимого P L -модуля с q -ограниченным старшим весом неприводимо, и совокупность таких ограничений образует полный набор неприводимых P L -модулей. Далее M(w) обозначает ограничение на L неприводимого PL-модуля со старшим весом w из этой совокупности.

Лемма 8. Пусть n = 2, h — полупростой элемент нечетного порядка k из L и M(w) — неприводимый PL-модуль со старшим весом w = aw i , где 1 с a < q. Предположим, что a = ^ j — Q a j p j — p-адическое разложение числа a. Тогда

• (1)    если p нечетно, то Z(L) лежит в ядре представления группы L, соответствующего модулю M(w), тогда и только тогда, когда число a четно;

• (2)    элемент h имеет ненулевую неподвижную точку в M(w) тогда и только тогда, когда существует такое неотрицательное целое число b, что bk с a, a — bk четно и (a — bk)/2 = ^ j =Q b j p j , где 0 с b j с a j для всех j = 0,..., l — 1.

• <1 Утверждение (1) хорошо известно (см., например, [19, лемма 7]).

• 3. Доказательство теоремы

Утверждение (2) следует из [20, теорема 3]. >

Нам понадобится также следующий фрагмент таблицы комплексных неприводимых характеров группы SL 2 (t), где t нечетно, z — единственная инволюция из SL 2 (t), a и b — элементы порядков t — 1 и t + 1 из SL2(t) соответственно и е = ( — 1) ^(t-1)/2 (см. [21, §38] или [22, табл. 4]).

Таблица 1

Фрагмент таблицы характеров группы SL 2 ( t ) при нечетном t

	1	z	a m (1 с m с (t - 3) / 2)	b n (1 с n с (t - 1) / 2)
1	1	1	1	1
ψ	t	t	1	- 1
χ k	t +1	( - 1) k ( t + 1)	2 cos 22^	0
(1 с k с ( t - 3) / 2)
θ l	t - 1	( - 1) l ( t - 1)	0	- 2 cos 2^
(1 с l с (t - 1) / 2)
ξ 1	(t + 1) / 2	e ( t + 1) / 2	( - 1) m	0
ξ 2	(t + 1) / 2	e ( t + 1) / 2	( - 1) m	0
η 1	(t - 1) / 2	— e ( t — 1) / 2	0	( - 1) n +1
η 2	(t - 1) / 2	- s ( t — 1) / 2	0	( - 1) n +1

Пусть G — группа, удовлетворяющая условиям теоремы, и S = S (G).

Предположим, что q = 2. Тогда p = 3 и S = 0(G). Поскольку в G есть четверная подгруппа, ввиду [12, теорема 5.3.16] имеем S = 0 3 (G) и, следовательно, | n(G) | = 4. Но числа r и s больше 3, поэтому они делят | G | , смежны в графе r(G) и не смежны с 2 в этом графе. Если граф r(G) несвязен, то это противоречит [7, 8]. Если граф r(G) связен, то это противоречит [23].

Итак, q = 3, следовательно, p = 2 и r,s> 3. Если r и s не делят | S | , то S = 0 2 (G), следовательно, n(G) = n(G) и вершины r и s смежны в графе r(G), что противоречит [7] или [23]. Поэтому без ограничения общности можно считать, что r делит | S | . Пусть Q G Syl 3 (G). Разрешимая группа SQ содержит {r,s, 3 } -холлову подгруппу U . Так как граф Г(и) несвязен, а W := U И S является нормальным 3-дополнением в U , на котором неединичные элементы из Q действуют без неподвижных точек, по теореме Грюнберга — Кегеля [24, теорема A] подгруппа U является группой Фробениуса с ядром W и дополнением Q . По свойствам группы Фробениуса (см., например, [12, теорема 10.3.1]) W = F(U ) = O r (W ) х O _s (W ) и Q — циклическая 3-группа. Отсюда ввиду [3, 6—8, 23] следует, что цоколь L группы G изоморфен одной из групп L 3 (5), L 3 (17), и з (7) или L2(t), где либо t G { 8, 25,49 } , либо t ^ 5 — простое число такое, что | n(t ² — 1) | С 3. Поскольку W является {r, s } -холловой подгруппой в S , а все такие подгруппы в разрешимой группе S сопряжены, имеем G = SN g ( W ) и, следовательно, G = SN g ( W )/S = N g ( W ) /N s (W).

Пусть N = N g ( W ). Тогда S(N ) = N s (W) = W x P , где P G Syl 2 (S(N )). Ясно, что

O r ’ (S (N)) = O s (W)C p (O r (W)) и O r ‘ ,r (S(N )) = O r ’ (S(N))O r (W).

Ввиду [12, теорема 6.3.2] имеем C s ( n ) (O _r (W)) С O r ’ ,r (S(N ))• Положим N = N/O _r ‘ (S(N )). Тогда

S(N) = O r (W)P = O r (N) x P и C N (O r (N))< O r N).

Если L = L 2 (5), то утверждение теоремы выполняется. Поэтому в дальнейшем будем считать, что L ^ L 2 (5).

Предположим, что L = L 2 (7). Тогда можно считать, что r не делит | L 2 (7) | . Поскольку ввиду [11] группа L 2 (7) содержит группу Фробениуса F порядка 21, группа N содержит подгруппу вида O r (N ) x F . Но тогда ввиду леммы 5 группа N содержит элемент порядка 3r. Получили противоречие. Поэтому L ^ L 2 (7).

Пусть x — элемент порядка 3 из Q . Можно считать, что x нормализует подгруппу P . Рассмотрим подгруппу O r (N ) x (P x (x)).

Покажем сначала, что [P, ( x ) ] = 1. Предположим противное, т. е. [P, ( x ) ] = 1.

Пусть C — критическая подгруппа в 2-группе P (см. лемму 3). Применим леммы 3 и 4 к подгруппе Or (N) x (P x (x)). Тогда C — характеристическая подгруппа в P, [P, C], Z(P), Ф(С) c z(C) c CP(x) и [C, (x)] = Q8. Подгруппы Or(NC) и Or(NZ(C)) нормальны в группе N. Положим H = N/Or(NZ(C)), V = Or(NC)/Or(NZ(C)). Тогда V — нормальная элементарная абелева 2-подгруппа в H, Ch(V) = O2(H) и H/O2(H) = G. В частности, V есть точный GF(2)L-модуль такой, что |[V, (x)]| = 4 для (x) = Qi(Q). Ясно, что циклическая 3-группа Q точно действует на четверной группе [V, (x)], поэтому |Q| = 3. Отсюда следует, что группа L не изоморфна группам L2(8), L2(17) и L3(17), силовские 3-подгруппы которых циклические порядка 9. Ясно, что модуль V имеет композиционный фактор V0 размерности, не меньшей 2. Пусть K — алгебраическое замыкание поля GF(2). По лемме 2 для точного неприводимого GF(2)L-модуля V0 существует класс {Wi,..., Wm} алгебраической сопряженности точных (абсолютно) неприводимых KL-модулей с полем определения GF(2m) такой, что Vo 0gf(2) K = Omi Wi- Обозначим через Wo модуль Wi, рассматриваемый как GF(2m ^-модуль. Тогда модуль Vo можно отождествить с модулем Wo, рассматриваемым как GF(2)L-модуль. Поэтому мы имеем dim Vo = m dim Wo и dim Cy0 (x) = m dim Cw0 (x). Следовательно, dim[Vo, (x)] = dim Vo — dim Cv0 (x) = m(dim Wo — dim Cw0 (x)) = 2.

По таблицам 2-модулярных брауэровых характеров групп L a (5) и U a (7) (см. [15]) и лемме 1 легко получаем, что эти соотношения в случае, когда группа L изоморфна L a (5) или U a (7), не выполняются. Поэтому L = L 2 (t), где либо t € { 25,49 } , либо t — простое число такое, что t >  7 и | n(t ² — 1) | =3. Применяя нашу таблицу 1, 2-модулярную матрицу разложения группы L 2 (t) из [25, раздел VIII] и лемму 1, приходим к противоречию с доказанным выше соотношением dim[V o , ( x ) ] = 2.

Итак, [P, ( x ) ] = 1. Поэтому цоколь почти простой группы N/S(N ) централизует фактор-группу S(N )/O r (N). Пусть E — последний член ряда коммутантов группы N/O r (N ), т. е. E — слой этой группы. Тогда E — квазипростая группа такая, что E/Z(E) = L, и F * (N )/O r (N ) = (S(N )/O r (N7)) о E. Ввиду [11, таблица 5] группа E изоморфна L a (5), L a (17), U a (7), L 2 (t) или SL 2 (t). Если группа E изоморфна L a (5), L a (17) или U a (7), то по [10, таблицы 8.3, 8.5] имеем A 4 < E, откуда ввиду леммы 5 группа N содержит элемент порядка 3r. Получили противоречие. Если E = L 2 (t), то ввиду лемм 6 и 7 в группе G есть элемент порядка 3r. Получили противоречие. Поэтому E = SL2(t) и t нечетно.

Предположим, что r не делит t. Ясно, что 3 делит t ² — 1. Если 3 делит t — 1, то E содержит группу Фробениуса вида T : 3, где T — силовская подгруппа порядка t в E, откуда ввиду леммы 5 группа N содержит элемент порядка 3r. Получили противоречие. Поэтому 3 делит t + 1 и, следовательно, t > 7 — простое число и r либо не делит | E | , либо делит t — 1 (поскольку группа E имеет точно один класс циклических подгрупп порядка t + 1, а вершины r и 3 не смежны).

Предположим, что r делит |E|. Тогда r делит t — 1 и s = t > 7. Пусть R € Sylr(E). Можно считать, что Ce(R) = (a). Поэтому каждый r-блок B характеров группы E имеет циклическую дефектную группу D(B), лежащую в R, и, следовательно, порядок группы Ne(D(B))/Ce(D(B)) не превосходит 2. По теореме Дейда [26, теорема 68.1] число вершин дерева Брауэра каждого r-блока характеров группы E равно 1 или 3 и, следовательно, каждый неприводимый r-модулярный брауэров характер группы E совпадает с ограничением некоторого комплексного неприводимого характера группы E на множество E\r‘ всех r’-элементов этой группы. Пусть Vp — абсолютно неприводимый E-модуль c r-модулярным брауэровым характером β , на котором элемент x действует свободно. Тогда ввиду леммы 1 имеем dim Cv,(x) = e(1) + 2e(x) = 0. в' 3

Отсюда в(1) + 2в(x) = 0. Но в = xIe | ‘ для некоторого х € Irr(E). Можно считать, что x = b ^(t+1)/a . Из таблицы 1 легко видеть, что 1 e (x) = 1, ^(x) = — 1, X k (x) = 0 для всех k, d i (x) равно 1 при l = ± 1(mod3) и — 2 при l = 0(mod3), £ i / 2 (x) = 0, n ₁ / ₂ (x) = ( — 1) ^(t+1)/a + 1. Поскольку в(1) + 2e(x) = 0, получаем, что t = 5 = r; противоречие.

Таким образом, r не делит |E|. Тогда \n(E)\ =3 и, следовательно, ввиду [6] имеем t = s = 17. Каждый неприводимый r-модулярный брауэров характер в группы E совпа- дает с некоторым комплексным неприводимым характером группы E . Рассуждая, как в предыдущем абзаце, получим противоречие.

Итак, можно считать, что r делит t и s не делит | S | . Поэтому | п(Е) | = 4. Имеем t = r^l, где l = 1 при t = r и l = 2 при t G { 25,49 } . Применим лемму 8 при k = 3. Пусть K — алгебраическое замыкание поля GF(r) и M (ш ) — точный неприводимый KE -модуль со старшим весом ш = aw i (1 С a < t), на котором элемент x порядка 3 из E действует свободно. Предположим, что a = £^0 a j r^j — r-адическое разложение числа а. Покажем, что a =1 при t = r и a G { 1,r } при t G { 25,49 } . Предположим противное. Тогда 1 = a = r. По п. (1) леммы 8 число a нечетно. Покажем, что выполняется условие п. (2) леммы 8 о существовании для x ненулевой неподвижной точки в M (ш). Если t G { 25,49 } , то выполнимость этого условия проверяется непосредственным перебором. Пусть t = r. Тогда a = a g и 1 < a < r. Пусть d — остаток от деления числа a на 3, т. е. a = 3c + d для некоторых неотрицательных целых чисел c и d, где 0 С d <  3. Если d = 0, то при b = c получаем, что 3b = a, a — 3b = 0 четно и (a — 3b)/2 = 0/2 = 0 < a g = a, т.

• е. проверяемое условие выполняется. Если d = 2, то при b = c получаем, что 3b < a,

a — 3b = 2 четно и (a — 3b)/2 = 2/2 = 1 < a g = a, т. е. проверяемое условие выполняется. Итак, d =1. Поскольку a > 1 нечетно, положительное число c четно и, следовательно, c >  1. Тогда a = 3c + 1 = 3(c — 1)+ 4 и при b = c — 1 получаем, что 3b < a, a — 3b = 4 четно и (a — 3b)/2 = 4/2 = 2 С a g = a, т. е. проверяемое условие выполняется. Полученное противоречие показывает, что a =1 при t = r и a G { 1,r } при t G { 25,49 } . Хорошо известно, что модуль M (ш 1 ) является естественным 2-мерным K E -модулем, а модуль M (rw i ) в случае t G { 25,49 } алгебраически сопряжен с M (w i ) посредством скручивания Фробениуса. Ввиду [27, предложение 4.7] все эти модули являются r ^′ -полурегулярными, т. е. все нетривиальные r ^′ -элементы из E действуют на них свободно. Отсюда следует, что вершины r и s не смежны в графе r(G). Получили противоречие.

Теорема доказана.