Конечные неразрешимые группы с нетривиальным центром и малыми централизаторами нецентральных элементов

1. Введение и основные допущения. Через w(n) условимся обозначать количество множителей в представлении натурального числа и в виде произведения простых чисел. Если Н- подгруппа конечной группы G, то w(H) = w(|7/|) и v(G) = max| w(C(g))| g e G \ Z(G)}.

О)

В работах [1] и [2] исследованы конечные неабелевы группы с условием v(G) = 2 и v(G) = 3 соответственно. В [3, 4] описаны конечные группы с условием v(G) = 4, а в работах [5] и [6] изучены неразрешимые группы без центра с условием v(G) = 5. В предлагаемой работе исследуется строение неразрешимых групп с нетривиальным центром и с условием v(G) = 5.

Если р - нечетное простое число, то положим

max-!

если р^п = 1(4),

max-

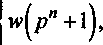
Кроме того, положим

Z*^n) = max^w^"-l),w^” + l

Через Е^ условимся обозначать элементарную абелеву группу порядка р^п. В дальнейшем р- всегда нечетное простое число.

Пусть G - неразрешимая группа, v(G) = 5 и 2(G)# 1. Предположим, что Z₂(G)>Z(G). Если xeZ₂(G)\Z(G) и ^:g->[g,x], то Кег(^) = С(х) и G/C(x)-абелева группа. Но тогда подгруппа С(х) неразрешима. Так как С² (х) = С(С(х))~ абелева группа, то фактор-группа Н = С(х)/С²(х) неразрешима. Из условий м(С(х))<5 и w^C²(x)j>2 следует, что м(Я)<3, что противоречит неразрешимости группы Н. Поэтому Z₂(G) = Z(G) и G/Z(G)-группа без центра. Отметим еще, что v(G/Z(G)) < v(G). Это следует из того, что

|^g/z(g) №))|-

|C(x)|-|z(G)n{[x,g]|geG}|

№

Тюрина И.А.

В самом деле, пусть H/Z(G^ = C_G;z^ycZ(Gjy Рассмотрим гомоморфизму: Н ->Z(G), заданный формулой ^=[h,x]. Тогда Кег(у) = С(х) и Im у={[х,Л]|йеЯ] = = {[*’ s] |g ё G} n Z (G). Поэтому |Я|=|С (х)| ■ |z (G) л {[х, g]|g е G}|.

Из работ [1-6] следует, что неразрешимые конечные группы без центра с условием v(G) = л < 5 исчерпываются группами следующих типов.

• А.    Простые группы.

• 1)    л = 2: PSZ(2,5);

• 2)    л = 3: PSL(2,₉), 9е[2³,3²,3³,5³,р),где Z(p) = 3;

• 3)    л = 4: А_ч\PSL^q), ₉е{2⁴,5²,7³,^}, где 7(/?) = 4;

• 4)    л = 5: M_n; ^; РЗЦЗ.З); PSL(2,q), qe^3⁴,7²,n\\3²,p^, где 1^ = 5; Р8Ц2,р^зу где /(р³) = 5; PSL^p⁵^, где р=2 или /|у⁵)<5.

• В.    Группы автоморфизмов простых групп.

• 1)    л = 3: PGZ(2,5);

• 2)    л = 4: PGL^qy де{з²,3³,р|, где Z*(p) = 3; PSL(2,q)A(Ty ^е|2³,3³|, г-полевой автоморфизм порядка 3; PSL ^2,3²)-(^, где Г-произведение полевого и диагонального автоморфизмов;

• 3)    л = 5: PGL^q^, #е|5²,5³,7³,/>|, где 1*^ = 4; Р8Ц2^А^тУ ^е^2⁴,3²|, г-полевой автоморфизм порядка 2; PSL^2,5² У^ , где t- произведение полевого и диагонального автоморфизмов; Aut (PSZ (2, д)), 0б|з²,3³|.

• С.    Расширения группы ^.

л = 5: А^хН, Я-неабелева группа порядка pq\ ^A^x^a^-^ , где ^-(г)^^, ^ = р, т инвертирует a.

• D.    Расширения абелевых групп.

• 1)    л = 4: Е_р3 APSL(2,5), р ее ±1(10); О/Е₅з = PSL^S);

• 2)    л = 5: HASEKS')- группа Фробениуса и 2E^ASL^.Sy, ^E_s2xE_p2^ZSL(2,Sy Е_р2 ASL(2,5)-группа Фробениуса; ((a)x(Z>))ZSZ(2,5), |а| = [/>| = 25; две группы типа £₅4 2SZ(2,5); две группы типа Е_рА ASLIS'), р*5; £^₃ Z((o)xPSZ,(2,5)), р = ±1(10), ysl(3), |«| = 3, Е_рзА(^- группа Фробениуса; £^₃ZP5Z(2,7), /?³=1(7); С/Е₅з =PGL(2,5).

• 2.    Основная теорема. Целью данной работы является доказательство следующей теоремы.

В пункте D действие соответствующих групп на абелевой группе определено в работах [5-7].

ТЕОРЕМА. Пусть G-конечная неразрешимая группа с нетривиальным центром. Если v(G) = 5, то G - одна из следуюгцих групп:

• 1)    G = HxZ^Gy Н-группа одного из типов А.1)-А.З) илиD.l), w(z(G)) = 5-v(^);

• 2)    GIZ(G)~   группа одного из типов В.1) или S.2), G'nZ(G) = l и

• w(z(G)) = 5-v(G/Z(G));

• 3)    G = H-Zpy H = SLp,q^ и w(z(G)) = 4, если q = 5; w(z(Gy = 3, если q = p, 1*^ = 3; w(z(G)) = 2, если 9е[з³,5²,5³,7³,р), где ЦррА; w(Z(G)) = l, m.e. G = SL(2,qy если q е|з⁴,7²,ll²,IS²,^, p^, где р_х,р_г-нечетные простые числа, I'^p^pS ul*^p^ = 5;

• 4)    С = А₂/(к"У где A₂-универсальная накрывающая группы А₂, ^- мультипликатор Шура группы А₂, а п е {2,3,6};

• 5)    G = H-Z^G\ где либо HaPSL^* или SLp.^ и w(z(G)) = 3, либо Н = Р8Ц2,9У 1^ или w(z(G)) = 2;

• 6)    GIZtp^PGLpl^ и G' = SL^2,qy при этом w(z(G)) = l, если 9б^5²,7³,р|, где Г^р^А; w(z(G)) = 2, если ^е^3³,5³,р|, где f^jp = 3; w(Z(G)) = 3, если q = 5;

• 7)    GfZ^sPGL^ и при этом либо G'sSL^^wiu PSL(2,9)* и w(Z (G)) = 2, либо G' = PSL(2,9y/^и w(Z(G)) = l;

• 8)    G = SL^q^Apy ^e^3²,3³|, т- нетривиальный полевой автоморфизм;

• 9)    GIZp^PSL^qyip, #е|з²,5³^, t- произведение полевого и диагонального автоморфизмов, и если ^ = 5², то G* = SL^2,5²^ и w(Z(G))=l, а если q = 3², то G' = PSL(2,9)*/(к"У где Ле{2,3,б} и w(Z(G)) = 2;

• 10)    G = E_p3ASL(2,5y р = ±1(10) и С^Е_р3^ = Е_р3 Ару где т- инволюция из SL(2,5y

Доказательство. Если Z (G)n G* = 1, то

Co,z(=)(^(G)) = CW/Z(G)                        (5)

для любого xeG, т.е. v(G) = v(G/Z(G)) + w(z(G)). Поэтому фактор-группа G/Z(G) в этом случае изоморфна одной из групп А.1) - А.З), В.1), В.2) или D.1) и w(Z(G)) = 5-v(G/Z(G)). Если при этом G/Z(G) совпадает со своим коммутантом, т.е. является группой типа АЛ) - А.З) или D.1), то из равенства G = G'-Z(G) следует, что G = G'xZ(G). Таким образом, в случае Z(G)nG' = 1 группа G является группой типа 1) или 2) из условия теоремы.

Предположим теперь, что Z(G)r>G'*l, и пусть G/Z(G)- группа одного из типов АЛ) -А.4). Тогда G = G'-Z(G) и G' является накрывающей для группы G/Z(G). Случаи G/Z(G) = A/_H, J_x, PSL^^ или PSL^2,2ⁿ^ при и>2 невозможны, так как в этих случаях мультипликатор Шура группы G/Z(G) тривиален.

Пусть G/Z(G) = PSL^2,q^, q = pⁿ нечетно и отлично от 9. Тогда G' = 8Ь(2^ . В этом случае (см., например, доказательство теоремы 5.9 из [8]) централизатор любого нецентрального элемента х в группе G абелев и

IcM/ZtGJlelgri.til}.                     (6)

Тюрина И.А. Конечные неразрешимые группы с нетривиальным центром и малыми централизаторами нецентральных элементов

Поэтому G = 81(2^ ■ Z (G). И из равенств

Предположим теперь, что G/Z (G) = А, . Группа А_ч имеет три накрывающие с центрами порядков 2, 3, и 6, соответственно. Заметим, что элемент простого порядка г из Z(G)nG' увеличивает на единицу значение w(C(x)) для г'-элемента х из А_ч и не меняет w(C(x)) для элемента х порядка г . Так как в группе А_п для элементов порядка 2 и 3 выполняется равенство w(C(x)) = 4, то в любом случае v(G') = 5 , т.е. G = G' = A^l(kⁿ^ , где (£) - мультипликатор Шура группы А-] и и е {2,3,6}, т.е. G- группа типа 4 из условия теоремы.

Пусть G/Z(G) = P5Z(2,9). Мультипликатор Шура группы PSZ(2,9) тоже является циклической группой порядка 6. Так как в группе PSL^2,9^ для элемента х порядка 3 выполняется равенство м(с(х)) = 2, а для элемента х порядка 2 - равенство w(C(x)) = 3, то v(G') = 4 в случае G' = PSL(2,9^ или PSZ(2,9) /^³^ где ^- мультипликатор Шура группы Р8Ь(2,9У и v(G') = 3 в случае G' г PSL(2,9) /^²^, т.е. в этом случае G - группа типа 5 из условия теоремы.

Пусть теперь G/Z^G^sPGL^qy Тогда G'-Z^G^/Z^G^PSL^q^. Положим G'-Z^G^H. Тогда Н*-Z^G^H и НIН' -центральная подгруппа порядка 2 из GIH*. Поэтому GIH'- абелева группа, т.е. H' = G'. Но тогда G" = Н" = Н* = G'. Отсюда G* nZ(G) = G" nZ(G') и, следовательно, G* является накрывающей для группы G7 (G'n Z (G)) = PSZ (2, ^).

Если q*9, то снова G' = SL(2,qy В этом случае (см. доказательство теоремы 5.9 из [8]) централизаторы нецентральных элементов в группе G исчерпываются подгруппами порядков «■|z(G)|_H(_g±l)|Z(G)|,T.e.мы получаем группы типа 6) из условия теоремы.

Предположим, что q = 9. Тогда G' = PSZ(2,9) /^"^ ^гД^е не {2,3,6}. Если и = 3, т.е. G' = SL(2,9y то из /*(9) = 3 следует, что w(z(G)) = 2. А если G'sPSZ(2,9) или PSL (2,9) 7^²^ иг- центральная инволюция из G/Z(G), то из условия |c_g/Z(_G)(tZ(G))| = 16 следует, что порядок силовской 2-подгруппы S из С (г) равен 16. Так как C(r) = 5’-Z(G) и |Z (G) n G'j равен 6 или 3, то

|C(r)| = 48-|z(G)/(z(G)nG')|. (8)

Поэтому из w(48) = 5 следует, что Z(G)в первом случае и w(Z (G)) = 1 во втором случае, т.е. G - группа типа 7 из условия теоремы.

Рассмотрим теперь случай, когда G/Z(G) = P»SZ(2,^)Z(t). В этом случае снова G'- эпиморфный образ PSL(2,q} . И из равенства PSL^2,2ⁿ^ = PSL[2,2"} при п>2 следует, что q = 3^T или З³. Если q = 3³, то из C(r)^(T)xSZ(2,3) и условия v(G) = 5 следует, что w(Z(G)) = l, т.е. С = 8Ь(2,зЛЦту В случае и q = 9 и G' = 5Z(2,9) аналогично получим

Математика______________ _____________________________

G = SL(2,9)^t}. А если О' = Р8Ц2,9^ или PSZ^.g)*/^²), то из С _psl^^ = PGL (2,3) получим v(G)>5.

Пусть G/Z(G) a P5Z(2,^)0, где t- произведение полевого и диагонального автоморфизмов. В этом случае силовская 2-подгруппа группы G/Z(G) диэдральна. Как и выше, G'-эпиморфный образ группы. В случае q = 5² для центральной инволюции Т&G/Z(G) выполняется равенство |С(/)| = 24 • |Z (G)|, т.е. в этом случае w(Z (G)) = 1. Если же q = 9, то |C(/)|=8.|Z(G)| и, следовательно, w(Z (G)) = 2.

Пусть GIZ^G^^xH, |я| = /?^.Если а - элемент порядка 3 из Н, g- элемент порядка q из ^ и z = [a,g], то из z^p = ^a^p,g^ = l = ^a,g⁹"^ = z⁹ следует, что либо г = 1,либо q = p. Во втором случае элемент а перестановочен с силовской 2-подгруппой из Т, где Т = А₅х(а}, а следовательно и с подгруппой, порожденной этими силовскими 2-подгруппами. Но тогда С(а) = Т(а) и w(C(a))>5, т.е. этот случай невозможен. В случае G/Z(G) = (77x(a))(r), где Н = А₅, аналогично получим C(a) = Н х (а), что невозможно.

Пусть G/Z(G)-расширение группы 0₃,где р = 5 или р г±1(10), с помощью PSL(2,sy Как показано при доказательстве теоремы 1.2 из [3], в этом случае можно считать, что Е_р3 = ^i)x^a₂^x^a₃^ ’ ^и Д™ силовской 2-подгруппы р^х^т₂^ из PSZ(2,5) выполняются равенства а/' = о, и а^ = а, ¹ при i* j , где /,_/ = 1,2,3 и т₃=т₁-т₂. Но тогда из ^a,,a^eZ(G) следует, что

[a,.,ay] = [a,.,ayp ф^а/].                            (9)

Поэтому ^а_оа^ = 1, т.е. (|G'nZ(G)|,pj = l. Это означает, что |G'nZ(G)| = 2 и G- расширение Ру с помощью SL(2,5), причем инволюция из 57(2,5) действует на Е_р3 тривиально, т.е. G-группа типа 10) из условия теоремы.

Если GIZ(G) = AXSL^2, 5)-группа типа D.2), то из SZ(2,5) = 57(2,5) следует, что порядок |G'nZ(G)| нечетен. Но тогда если т- инволюция из SL (2,5), то w(C (г)) > 5, т.е. этот случай невозможен. Аналогично в случае G/Z(G) = £^₃ 2((a)xPSZ(2,5)) получим w(C(a))>5.

Предположим теперь, что G/Z(G) = Е^ APSL(2,7^ . Из леммы 6.5 работы [7] следует, что в некотором базисе ^а_;,а₂,а₃^ группы Е_р3 элемент х порядка 4 из PSZ(2,7) задается матрицей

-г —— о г А -г-1 ,

I 22)

где г - решение уравнения 2г²+г + 1 = 0 в поле GF^pY Но тогда C_GI2^^ = = (х}х(а_]^га^а₃\. Положим b =а_}^га^а₃. Так как ’w^C_Glz^_G^^ = S и »(C(6))S5, ТО

Тюрина И.А.

G'nZ(G) = (z)- подгруппа порядка р и z = [6,c] для некоторого элемента с ^Е_ръ- Но тогда, если Р- силовская /7-подгруппа группы G, то [Р,х]^С(0. И из Р = [Р,х]-С_р(х) и С_Р (х) = (b, z^ следует, что Р < С(б), что невозможно.

Случай G! Е^ =PGL^,5^ аналогично приводится к противоречию. В этом случае из леммы

• 6.3.    работы [7] следует, что в некотором базисе |а₁,а₂>«₃| группы Е^ элемент х порядка 4 из

PGZ(2,5) задается матрицей

/ 3 -1   Г

3 0-1

I-1   3   3>

т.е. Cy/z^(x) = (x)x/a12a3\. Теорема доказана.