Конечные полумодули над трехэлементными мультипликативно идемпотентными полукольцами

Введение. Основные понятия

Исследуются полумодули над трехэлементными мультипликативно идемпотентными полукольцами. Статья примыкает к работам [1], [2]. Теория мультипликативно идемпотентных полуколец излагается в книге [3]. Ранее изучались гомологические свойства полумодулей над дистрибутивными решетками S , называемых S -полигонами [4], в частности над трехэлементной цепью [5]. Последние достижения в теории полигонов над полугруппами изложены в обзоре [6]. Обзорная статья [7] посвящена теории полумодулей над полукольцами.

Отметим, что базовую информацию о полукольцах и полумодулях можно найти в монографии [8], а по теории решеток – в книге [9].

Полукольцом (с нулем и единицей) называется алгебраическая структура ( S , +, •) с двумя бинарными операциями сложения + и умножения и элементами нуль 0 и единица 1, удовлетворяющими следующим условиям:

• 1)    ( S , +, 0 ) - коммутативный моноид;

• 2)    ( S , •, 1 ) - моноид;

• 3)    0 – мультипликативный нуль, то есть тождественно 0· x = x ·0 = 0;

• 4)    умножение дистрибутивно относительно сложения с обеих сторон, то есть в S справедливы тождества ( x+y ) z = xz+yz и x ( y + z ) = xy + xz .

Полукольцо S называется:

• •    коммутативным , если S удовлетворяет тождеству xy = yx ;

• •    мультипликативно идемпотентным , если в S тождественно xx = x ;

• •    идемпотентным , если S удовлетворяет тождествам xx = x и x + x = x .

Полумодулем над полукольцом S или просто S-полумодулем (унитарным левым S -полумодулем) называется коммутативный моноид ( A, +, 0 ) с нейтральным элементом нуль 0 вместе с отображением S х A ^ A , ( s , a ) ^ sa , обладающим следующими свойствами (для любых s, t g S и a , b g A ):

• (1)    ( s + t ) a = sa + ta ;

• (2)    s ( a + b )= sa + sb ;

• (3)    ( st ) a = s ( ta );

• (4)  1· a = a ;

• (5)    0· a =0= s ·0.

Отметим, что в полукольцах и полумодулях нуль 0 обозначается одинаково.

Заметим также, что такие понятия как полугруппа, моноид, идеал, подполурешетка, подполумодуль определяются стандартно.

Отображение a : A ^ B S -полумодуля A в S -полумодуль B называется S-гомоморфизмом , если а аддитивно и линейно , то есть a ( x+y )= a ( x)+ a (y ) и a ( sx )= s a ( x ) для любых x, y e A и s e S . Если S -гомоморфизм a S -полумодулей является взаимно однозначным отображением (биекцией), то он называется S-изомофизмом ; при этом обратная биекция а ^-1 также будет S -изомофизмом. Изоморфные S -полумодули имеют одни и те же абстрактные свойства.

Заметим, что класс всех S -полумодулей при фиксированном полукольце S образует категорию полумодулей, если в качестве ее морфизмов взять всевозможные S -гомоморфизмы.

Идемпотентная коммутативная полугруппа ( A , + ) называется полурешеткой . Эквивалентное «порядковое» определение: (верхняя) полурешетка - это упорядоченное множество ( A , <) , для любых элементов а и b которого существует точная верхняя грань sup( a, b ). Эти определения связаны соотношениями: а < b « а+b = b и а+b =sup( a, b ). Нулем полурешетки ( A , + ) называется ее нейтральный элемент 0: а +0= а для всех a e A . В порядковом смысле 0 есть наименьший элемент полурешетки ( A , <) .

Решеткой называется алгебраическая структура ( S , +, •) , такая, что ( S , + ) и ( S , •) -полурешетки, согласованные посредством законов поглощения x + xy = x и x ( x + y )= x . Эквивалентное "порядковое" определение: решетка - это упорядоченное множество ( A , <) , для любых элементов а и b которого существуют точная верхняя грань sup( а, b ) и точная нижняя грань inf( а, b ), то есть ( A , <) является одновременно нижней и верхней полурешеткой. Имеют место соотношения: а < b ^ ab = а и ab =inf( а, b ).

Отметим, что решетки удобно рассматривать как алгебраические системы ( S , +, • , <  с согласованными друг с другом бинарными операциями сложения +, умножения • и отношением порядка < . В частности, в решетках неравенства можно почленно складывать и умножать: а < b , c < d влекут а + c < b + d , ас < bd .

Решетка с тождеством x (y + z )= xy+xz , равносильно, с тождеством x + yz =( x + y )( x + z ), называется дистрибутивной .

Предварительные результаты

Приведем несколько предварительных соображений.

Лемма 1. Коммутативный моноид ( A , +, 0 ) будет S-полумодулем над некоторым мультипликативно идемпотентным полукольцом S тогда и только тогда, когда в A верно тождество 4 x =2 x.

Доказательство. В любом мультипликативно идемпотентном полукольце S имеем 4=1+1+1+1=(1+1)(1+1)=1+1=2. Поэтому полумодули над таким полукольцом S удовлетворяют тождеству 4 x =2 x . Обратно, если в коммутативном моноиде A верно тождество 4 x =2 x , то A будет S -полумодулем для четырехэлементного полукольца S ={0, 1, 2, 3} с равенством 3+1=2.

Далее предполагается, что A =( A , +, 0 ) - коммутативный моноид с тождеством 4 x =2 x .

С точностью до изоморфизма существует четыре трехэлементных мультипликативно идемпотентных полукольца:

• •    S i ={0 < e <  1} - цепь;

• •    S 2 ={0, e , 1} при 1+1=1 и e +1= e ;

• •    S з ={0, 1, 2} при 3=1;

• •    S 4 ={0, 1, 2} при 3=2.

Полукольца S 1 , S 2 - идемпотентные (2=1+1=1), а полукольца S 3 , S 4 не являются идемпотентными (2 ^ 1).

Следующее утверждение очевидно.

Лемма 2. Коммутативный моноид A является S 1 -полумодулем и/или S 2 -полумоду-лем тогда и только тогда, когда A будет полурешеткой.

Лемма 3. Если A - конечная полурешетка с нулем , то ( A , <) будет решеткой.

Доказательство. Требуется доказать, что любые два элемента a , b е A имеют точную нижнюю грань inf( a , b ). Рассмотрим множество B всех нижних граней множества { a , b }. Поскольку 0 е B , то B не пусто. Тогда inf( a , b ) есть сумма всех элементов множества B . См. более общее утверждение [9, с. 44, лемма 14].

Возьмем S -полумодуль A над некоторым мультипликативно идемпотентным полукольцом S . Каждый элемент e е S индуцирует аддитивный эндоморфизм e : A ^ A , a ^ ea при a е A , такой, что e (0)=0 и e ( e ( a ))= e ( a ) для всех a е A . При этом образ e ( A ) служит множеством всех неподвижных элементов при действии эндоморфизма e . Отметим, что в случае дистрибутивной решетки S множество e ( A ) названо в статье [10] фиксатором элемента e е S .

Если элемент e е S коммутирует с каждым элементом из полукольца S , то эндоморфизм e : A ^ A будет S -гомоморфизмом. В случае коммутативного полукольца S отображение a : S ^ End S , сопоставляющее каждому элементу e е S S -гомоморфизм e : S ^ S , является изоморфным вложением полукольца S в полукольцо End S всех S -гомоморфизмов S ^ S , рассматриваемое с операцией поточечного сложения и композицией S -гомоморфизмов.

Пусть A будет S 1 -полумодулем ( S 2 -полумодулем). Структура полумодуля A полностью определяется действием элемента e на A , поскольку 0 действует как нулевой эндоморфизм и 1 как тождественный изоморфизм. Множество e ( A ) будет подполурешеткой полурешетки A , содержащей 0, такой, что e ( a ) < a (соответственно, a < e ( a )) для любого элемента a е A . Легко видеть, что эндоморфизм e : A ^ A является изотонным отображением , то есть сохраняет порядок: a < b ^ ea < eb для всех a , b е A . Кроме того, e ( A ) является подполумодулем S 1 -полумодуля (соответственно, S 2 -полумодуля) A .

Полумодули над полукольцом S1

Подполурешетку B полурешетки A назовем S i -подходящей , если A допускает структуру S i -полумодуля ( i =1, 2) и B = e ( A ).

Теорема 1. Подполурешетка e ( A ) произвольного S 1 -полумодуля A однозначно определяет действие элемента e на A. При этом для любого элемента a е A элемент ea будет наибольшим элементом множества { x е e ( A ) : x < a } .

Доказательство. Пусть a е A и B ={ x е e ( A ): x < a }. Имеем ea e B , поскольку ea < a и e ( ea )= ea . Если x e e ( A ) и x < a , то x = ex < ea в силу изотонности отображения e . Поэтому элемент ea будет наибольшим элементом множества B . Заметим, что первая часть теоремы 1 вытекает также из [10, замечание 1 к теореме 2].

Теорема 1 позволяют проверять, будет ли данная подполурешетка B полурешетки A с нулем S 1 -подходящей.

В случае произвольной конечной полурешетки A с нулем 0 ее подполурешетка B с 0 задает отображение e : A ^ A согласно теоремы 1. Значит, подполурешетка B будет S 1 -подходящей тогда и только тогда, когда отображение e аддитивно.

Пример 1. Рассмотрим булеву решетку A ={0, a, b, s } с наименьшим элементом 0, наибольшим элементом s и одной парой несравнимых элементов a , b . S 1 -подходящими подполурешетками в B являются в точности следующие: {0}, A , {0, a}, {0, b }. В первом случае e действует как 0 (нулевой эндоморфизм), во втором случае - как 1 (тождественный изоморфизм), в третьем случае e ( b )=0 и e (s )=a , в четвертом случае e (a )=0 и e (s )= b . Во всех случаях отображение e аддитивно. Получаем, с точностью до изоморфизма, три S i -полумодуля A .

Предложение 1. Идеалы любой конечной дистрибутивной решетки A являются S i -подходящими подполурешетками в ней.

Доказательство. Пусть B - идеал конечной дистрибутивной решетки A . Рассмотрим отображение e : A ^ A , определенное по правилу теоремы 1 при e ( A )= B . Очевидно, что e изотонно. Для проверки аддитивности отображения e возьмем элементы a , b е A . Положим c = e ( a + b ) e B . Имеем e ( a )+ e ( b ) < e ( a + b ) и ca , cb e B . Тогда, в силу дистрибутивности решетки A , c = ce ( a + b ) < c ( a + b )= ca + cb <  e ( a )+ e ( b ). Значит, e ( a + b )= e ( a )+ e ( b ).

Предложение 2. Все подполурешетки с нулем конечной полурешетки A с нулем являются S i -подходящими тогда и только тогда, когда A - цепь.

Доказательство . ^ . Предположим, что в полурешетки A найдутся несравнимые элементы a , b . Положим B ={0, a + b }. По условию подполурешетка B будет S i -подходящей. Тогда a + b = e ( a + b )= e ( a )+ e ( b )=0+0=0, противоречие. Значит, любые два элемента полурешетки A сравнимы, то есть A будет цепью.

^ . Пусть A - конечная цепь с нулем 0 и B - ее подполурешетка с 0. Зададим отображение e : A ^ A по правилу теоремы 1. Как уже отмечалось, такое отображение e является изотонным. Ясно, что изотонное отображение цепи в любую полурешетку аддитивно.

Следствие 1. Для любого натурального числа n > 2 n-элементная цепь допускает ровно 2^{п— 1} структур S i -полумодуля. Значит, существует, с точностью до изоморфизма, 2 ^{п— 1} S i -полумодулей, являющихся п-элементными цепями.

Подсчитаем число попарно неизоморфных S i -полумодулей A , имеющих не более 5 элементов. Их аддитивные моноиды ( A , +, 0 ) являются решетками, представленными на рисунке:

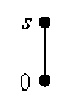
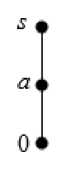
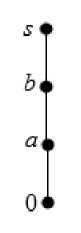
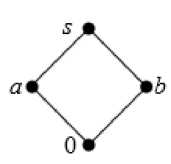
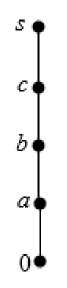
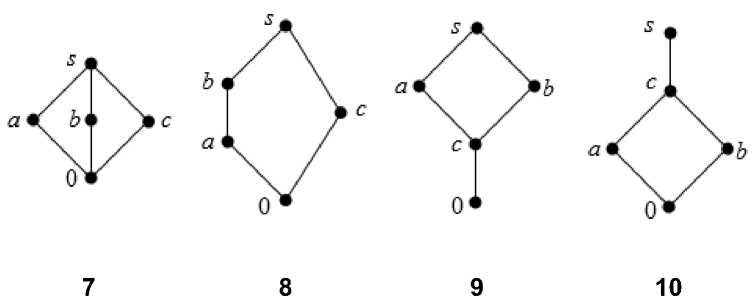
Диаграммы Хассе решеток мощности n < 5

Найдем для примера все неизоморфные S 1 -полумодули A , имеющие аддитивную структуру решетки 9 . Используя теорему 1, проверим, какие из ее подрешеток B с 0 могут выступать в качестве множества e ( A ).

Рассмотрим все возможные случаи.

• 1)    Пусть | B |=1, то есть B = e ( A )={0}. В этом случае e действует как нулевой эндоморфизм. Обозначим полученный полумодуль A 1 .

• 2)    Пусть | B |=2.

  • 2.1)    Если B ={0, c }, то e ({ a, b , s })= c и легко проверить, что e аддитивно, то есть имеем полумодуль A 2 .

  • 2.2)    Пусть B ={0, a }. Здесь e ({ b , c })=0, e ( s )= a и можно убедиться, что e аддитивно, получаем полумодуль A 3 . Ясно, что подрешетка {0, b } задает полумодуль, изоморфный A 3 .

  • 2.3)    Пусть теперь B ={0, s }. Имеем e ({ a , b , c })=0, и отображение e не является аддитивным, так как e ( a + b )= e ( s )= s ^0= e ( a )+ e ( b ).

• 3)    Пусть | B |=3.

  • 3.1)    Если B ={0, c , a }, то e ( b )= c , e ( s )= a , e аддитивно и имеем полумодуль A 4 , изоморфный полумодулю, получаемому в случае B ={0, c , b }.

  • 3.2)    При B ={0, c , s }, получаем e ({ a , b })= c и e не аддитивно, так как e ( a + b )= e ( s )= s ^ c = e ( a )+ e ( b ).

  • 3.3)    В случае B ={0, a , s }, получаем e ({ b , c })=0 и e не аддитивно, так как e ( a + b )= e ( s )= s ^ a = e ( a )+ e ( b ). Аналогично при B ={0, b , s }.

• 4)    Пусть | B |=4.

  • 4.1)    Если B ={0, c , a, s }, то e ( b )= c , но e ( a + b )= e ( s )= s ^ a = a + c = e ( a )+ e ( b ), то есть e не аддитивно. Аналогично при B ={0, c , b , s }.

  • 4.2)    Если B ={0, a , b , s }, то e ( c )=0 и имеем полумодуль A 5 .

• 4)    Пусть | B |=5, то есть B = A . Здесь e действует как тождественный эндоморфизм. Получаем полумодуль A 6 .

Таким образом, c точностью до изоморфизма существует ровно 6 S 1 -полумодулей, имеющих аддитивную структуру решетки A .

Предложение 3. С точностью до изоморфизма существует ровно 53 S 1 - полумодуля порядка ( мощности ) <  5. Из них :

• •    1 одноэлементный ;

• •    2 двухэлементных ;

• •    4 трехэлементных ;

• •    11 четырехэлементных, из которых 8 имеют ( аддитивную ) структуру решетки 4 и 3 имеют структуру решетки 5 ;

• •    35 пятиэлементных, из которых 16 имеют структуру решетки 6 , 2 имеют структуру решетки 7 , 5 имеют структуру решетки 8 , 6 имеют структуру решетки 9 и 6 имеют структуру решетки 10 .

Полумодули над полукольцом S2

Исследуем структуру S 2 -подходящих подполурешеток полурешеток с нулем.

Теорема 2. Подполурешетка e ( A ) произвольного S 2 -полумодуля A однозначно определяет действие элемента e на A. При этом для любого элемента a е A элемент ea будет наименьшим элементом множества { x е e ( A ) : a < x } .

Доказательство. Пусть a е A и B ={ x е e ( A ): a < x }. Имеем ea е B , так как a < ea и e ( ea )= ea . Если x e e ( A ) и a < x , то ea < ex = x . Поэтому элемент ea будет наименьшим элементом множества B .

Теорема 2 помогает убедиться в том, будет ли данная подполурешетка B полурешетки A с нулем S 2 -подходящей.

Пример 2. Рассмотрим цепь A , полученную из цепи Q рациональных чисел добавлением наименьшего 0 и наибольшего 1 элементов. Множество e ( A )= Z u { 0 , 1 } целых чисел с присоединенными элементами 0 и 1 является S i -подходящей подцепью S i -полумодуля A при i =1, 2.

Предложение 4. Пусть A - конечная полурешетка с нулем 0 и наибольшим элементом s. Тогда подполурешетка B полурешетки A будет S 2 -подходящей в том и только в том случае, когда B является подрешеткой решетки A и содержит элементы 0 и s.

Доказательство. Предположим, что подполурешетка B полурешетки A из условия предложения является S 2 -подходящей. По лемме 3 полурешетка A является решеткой. Имеем B = e ( A ), 0 е e ( A ) и s е e ( A ), так как s < es . Возьмем элементы a , b е B и покажем, что ab =inf( a , b ) е B . Поскольку ab < a = ea , ab < b = eb и ab < e ( ab ), то ab = e ( ab ) е B . Стало быть, B - подрешетка решетки A .

Обратно, пусть B - подрешетка конечной решетки A с наименьшим элементом 0 и наибольшим элементом s , содержащая 0 и s . Руководствуясь теоремой 2, определим отображение e : A ^ A , для любого элемента x е A положив ex = a 1 - _ - a k , где

{ a i - _ - a k }={a e B : x < a }. Отображение e изотонно и x < e ( x ) для всех x e A . Остается доказать аддитивность отображения e . Возьмем элементы x , y e A . Имеем e ( x )+ e(y ) < e ( x+y ). С другой стороны, x + y <  e ( x )+ e (y ) e B , откуда e (x + y ) < e (x )+ e (y ).

Пример 3. Пополним решетку A из примера 1 элементом c , таким, что 0 < c < a и c < b . В результате получим дистрибутивную решетку C , в которой верхняя подполурешетка A будет S i -подходящей, но не S 2 -подходящей в силу предложения 4. Цепь B ={0, c, s } в решетке C , будучи S 2 -подходящей по предложению 4, не является S i -подходящей.

Предложение 5. Для того чтобы в конечной полурешетке A с нулем 0 и наибольшим элементом s все подполурешетки с 0 и s являлись S 2 -подходящими, необходимо и достаточно, чтобы решетка A обладала следующим свойством:

a+b=s и ab= 0 для любых несравнимых элементов a, b e A. ( * )

Доказательство. Пусть A - произвольная конечная полурешетка с наименьшим элементом 0 и наибольшим элементом s . По лемме 3 A - решетка. Легко видеть, что выполнение свойства ( * ) равносильно тому, что либо A - цепь, либо множество A\ {0, s } является дизъюнктным объединением не менее чем двух цепей.

Необходимость. Предположим, что все подполурешетки полурешетки A , содержащие 0 и s , являются S 2 -подходящими. Тогда по предложению 4 все они будут подрешетками решетки A . Пусть a, b e A - несравнимые элементы. Если a+b + s или ab / 0, то подполурешетка {0, a , b , s } в A не является ее подрешеткой.

Достаточность вытекает из предложения 4, поскольку любое подмножество в A , содержащие 0 и s , образует подрешетку решетки A .

Следствие 2. Любое подмножество конечной полурешетки A с нулем 0 , наибольшим элементом s и свойствам ( * ) , содержащее 0 и s, является S 2 -подходящей полурешеткой.

Следствие 3. Для любого натурального числа n > 2 всякая n-элементная полурешетка со свойством ( * ) допускает ровно 2 ^{п— 2} структур S 2 -полумодуля.

Следствие 4. Для любого натурального п > 2 п-элементная цепь допускает ровно 2 ^{п— 2} структур S 2 -полумодуля. Значит, существует, с точностью до изоморфизма, 2 ^{п— 2} S 2 -полумодулей, являющихся п-элементными цепями.

Замечание 1. Теоремы 1 и 2 суть необходимые условия на S i -подходящую подполурешетку S i -полумодуля ( i =1, 2). Они позволяют проверять, будет ли данная подполурешетка полурешетки A (конечной или бесконечной) S i -подходящей.

Замечание 2. Рассмотрим подробнее п -элементную ( п > 3) полурешетку A со свойством ( * ) с наименьшим элементом 0 и набольшим элементом s . По лемме 3 A является решеткой. Очевидно, что в решетке A все подмножества, содержащие 0 и s , являются подрешетками, стало быть, по предложению 4 будут S 2 -подходящими подполурешетками.

В силу свойства ( * ) упорядоченное множество A\ {0, s }, рассматриваемое с индуцированным порядком, является дизъюнктным объединением п i одноэлементных максимальных цепей, п 2 двухэлементных максимальных цепей, ..., п п -2 ( п- 2)-элементных максимальных цепей, таким, что п 1 +2 п ₂+.+( п- 2) п_{п -2}= п -2. Некоторые из чисел n_i могут равняться 0. Значит, полурешетка A имеет ровно п i ! • п 2 ! • . • п к ! автоморфизмов. Легко видеть, что данная полурешетка A имеет ровно один автоморфизм тогда и только тогда, когда все ненулевые числа среди чисел п i , п 2 , ., п п -2 равны 1, другими словами, длины максимальных цепей в A\ {0, s } попарно различны.

В этом случае существует, с точностью до изоморфизма, ровно 2 n ² S 2 -полумодулей A . При n 1 = n -2 полурешетка A обладает ровно ( n -2)! автоморфизмами.

Предположим, что подмножество B полурешетки A , содержащее 0 и s , перемещается при действии автоморфизма а полурешетки A , а ( B ) ^ B . Тогда S 2 -подходящие (полу)решетки B и а ( B ) порождают изоморфные неравные S 2 -полумодули A . Поэтому число попарно неизоморфных n -элементных S 2 -полумодулей A может быть значительно меньше числа 2 ^{n- 2} из следствия 3. Например, в случае n 1 = n -2 все k -элементные подмножества K множества A\ {0, s } порождает одну-единственную, с точностью до изоморфизма, S 2 -подходящую (полу)решетку на A - ее подрешетку K и {0, s }, определяющую структуру S 2 -полумодуля A . Следовательно, существует, с точностью до изоморфизма, ровно n -1 S 2 -полумодуля A .

Найдем число попарно неизоморфных S 2 -полумодулей, имеющих не более 5 элементов.

Перечислим для примера все неизоморфные S 2 -полумодули A , имеющие структуру решетки 9 . По теореме 1 для этого достаточно указать, какие из ее подрешеток B с 0 могут выступать в качестве множества e ( A ). В силу предложения 4 - это в точности все подрешетки в A , содержащие элементы 0 и s , то есть {0, s }, {0, c , s }, {0, a , s }, {0, b , s }, {0, c , a , s }, {0, c , b , s } и A . Отметим, что подрешетки {0, b , s } и {0, c , b , s } задают полумодули, изоморфные полумодулям, задаваемым подрешетками {0, a , s } и {0, c , a , s }, соответственно. Таким образом, c точностью до изоморфизма существует ровно 5 S 2 -полу-модулей, имеющих структуру решетки A .

Предложение 6. С точностью до изоморфизма существует ровно 41 S 2 - полумодуль порядка <  5. Из них :

• •    1 одноэлементный ;

• •    1 двухэлементный ;

• •    2 трехэлементных ;

• •    7 четырехэлементных, из которых 4 имеют структуру решетки 4 и 3 имеют структуру решетки 5 ;

• •    30 пятиэлементных, из которых 8 имеют структуру решетки 6 , 4 имеют структуру решетки 7 , 8 имеют структуру решетки 8 , 5 имеют структуру решетки 9 и 5 имеют структуру решетки 10 .

Замечание 3 Мы также нашли все шестиэлементные S 1 -полумодули и S 2 -полумодули, опираясь на диаграммы Хассе всех 15 шестиэлементных решеток. Сделали это, во-первых, "вручную", как в предложениях 3 и 6. Во-вторых, с помощью компьютерной программы. Получилось, с точностью до изоморфизма, 127 S 1 -полумодулей и 158 S 2 -по-лумодулей.

Полумодули над полукольцами S3 и S4

В полумодулях над каждым из полуколец S з и S 4 действие элемента 2 определяется однозначно: x ^2 x = x + x .

Для полуколец S з и S 4 справедливы следующие утверждения:

Предложение 7. Коммутативный моноид ( A , +, 0 ) является S з -полумодулем тогда и только тогда, когда A удовлетворяет тождеству 3 x = x; при этом он допускает одну-единственную структуру S з -полумодуля.

Доказательство. В полукольце S 3 ={0, 1, 2} выполняется равенство 3=1. Поэтому любой S 3 -полумодуль удовлетворяет тождеству 3 x = x . Если моноид A удовлетворяет тождеству 3 x = x , то элемент 2 действует по однозначно определенному правилу x ↦2 x , превращая тем самым моноид A в S 3 -полумодуль.

Предложение 8. Коммутативный моноид 〈 A , +, 0 〉 является S 4 -полумодулем тогда и только тогда, когда A удовлетворяет тождеству 3 x =2 x; при этом он допускает одну-единственную структуру S 4 -полумодуля.

Доказательство повторяет доказательство предложения 7.

Следствие 5. Для любой мощности m мощность множества всех попарно неизоморфных S 3 -полумодулей ( S 4 -полумодулей ) мощности m равна мощности множества всех попарно неизоморфных коммутативных аддитивных моноидов с тождеством 3 x = x ( соответственно, 3 x =2 x ) мощности m.

Замечание 4. Полученные в статье результаты, в частности теоремы 1 и 2, могут быть полезны при исследовании произвольных полумодулей над идемпотентными полукольцами.