Конфликтные управляемые процессы второго порядка

В связи бурного развития научно-технического прогресса в мире математические методы стали важным средством в управлении сложных систем. В управлении многих экономических и технических процессов требуется учесть еще конфликтность различных сторон. В связи с этим создана новая область математики, т.е. теория конфликтных управляемых процессов описывающаяся дифференциальными и дискретными уравнениями. Более кратко эту теорию принято называть теорией динамических игр, которая слагается из двух компонент – теории дискретных и дифференциальных игр. В сегоднящних сложных рыночных отношениях при решении многих экономических и технических задач эти теории находят свои важные приложения. В настоящей работе рассматриваются движения объектов с ускорениями при геометрических ограничениях на управления. Получены новые достаточные условия для завершения игры, т.е. процесса в пользу преследующего объекта.

Пусть заданы объекты P и E с противоположной целью в пространстве R n и их движения описываются следующими дифференциальными уравнениями заданными начальными условиями и ограничениями на управления

P : x = u , x - kx ₀ = 0 ,  | u | <  а ,                       (1)

E : y = v , У 1 — кУ о = 0 , V <  в ,                     (2)

где    x, y, u, v g Rn; x - положение объекта P в пространстве Rn, x0 = x(0), xx = x(0) - его начальное положение и скорость соответственно при t = 0; и - параметр ускорения преследователя и оно выбирается как измеримая функция и : [ 0,»)^ Rn по отношению к времени t. Обозначим множество всех измеримых функций и (•), удовлетворяющих условию |и| < а, через U. у -положение объекта E в пространстве Rn, y0 = у(0), у = у(0) - его начальное положение и скорость соответственно в t = 0; v - контролируемое ускорение убегающего, v: [0, »)^ Rn и оно тоже выбирается как функция времени по отношению к t . Обозначим множество всех измеримых функций v(•), удовлетворяющих условию |v| < в, через V.

Определение 1. Для тройки (x0, x, и (•)), и (•) g U, следующее решение уравнения (1)

ts x (t) = x0 + x^ +

J j и ( r ) d r ds

0 0

называется траекторией преследователя на отрезке t >  0.

Определение 2. Для тройки ( y ₀, y₁ , v ( • )), v ( • ) е V , следующее решение уравнения (2)

ts

У (t) = У о + yit + J J v (т) dr ds о о называется траекторией убегающего на отрезке t > 0.

Определение 3. Задача преследования для дифференциальной игры (1) -(2) называется решённой, если существует такая управляющая функция преследователя и *(•) е U для любой управляющей функции убегающего

v(•) е V и в некоторый конечный момент времени t выполняется равенство x (t *) = У (t *)

Определение 4. Для задачи (1)  -  (2) время T называется гарантированным временем преследования, если оно равно верхней границе всех конечных значений времени преследования t *, удовлетворяющих равенству (3).

Определение 5. Для дифференциальной игры (1) - (2) следующая функция называется П-стратегией преследователя ([1] - [2]):

и ( v ) = v - Л ( v ) ^ о                            (4)

2  .   _ 2         2

^где ^ ^{( v} , ^ 0 ) = ^{( v} , ^ 0 ) ⁺ y^{( v} , ^ o) ^{+ а} |^v ’ ^ 0 = z о/| z o|

( v , ^ ) - скалярное произведение векторов v и ^ в пространстве R n .

Свойство 1. Если а >  в , то функция Л ( v , ^ ) непрерывна, неотрицательна и определена для всех таких v , что удовлетворяет неравенству I ^v l ^ ^в .

Свойство 2. Если а > в, то для функции  Л(v,^) справедливо неравенство:

а -| v | <  Л ( v , ^ ) < а + | v|

Теорема. Если для дифференциальной игры второго порядка (1) - (2) выполняется одно из следующих условий, 1. а = в и k <  0; или 2. а >  в и к g R , то с использованием стратегии (4) гарантированное время преследования будет следующим:

I ^ о I k + v | ² о f к ² + 2| z ₀ |( а - в ) ) / ( а - в ), если к ^ 0 и а > в, - 1 / к , если к <  0 и а = в , 7 2| z о| /( а - в ) , если к = 0 и а >  в .

Доказательство. Предположим, что преследователь выбирает стратегию в форме (4), когда убегающий выбирает любую управляющую функцию v ( • ) g V . Тогда согласно уравнениям (1) - (2) имеем следующее уравнение Каратеодори:

z = -Л ( v ( t ) ) ^ ₀,   z ( 0 ) - кг (0) = 0 ,

Отсюда при заданных начальных условиях будет найдено следующее решение ts

z ( t ) = z ₀( кt + 1) - ^ || Л ( v ( т ), ^ ) d r ds

0 0

или

I ^z ( t )| = I ^z 0 | ^{( kt} + 1) ^- jj ( ( ^{v ( т )}, ^ 0 ) ⁺ V ^{( v ( т} Ш^{2 + а 2 -} v ^{( т )}Г ) d ^T d^s •

Согласно свойствам 1 -2 сформируем следующие неравенства

I z ( t )| < | z ₀1 ( kt + 1) - fj ( a - v ( t )|) d r ds  ^

0 0

|z ( t )| < | z ₀1( kt + 1) + 1 ²( в — a ) / 2 .

Обозначим

f ( t , a , k , a , в ) = a ( kt + 1 ) —— ( a — в ) , a = | z ₀1.

• 1.    Пусть будет a = ft .

  • 1.1.    Если k >  0, то f ( t , a , k, a , в ) = a ( kt + 1 ) и это возрастающая функция (Рис-1)

ад

о                     t

(Рис-1)

• 1.2.    Если k = 0, то f ( t , a , k , a , в ) = |z ₀| - постоянная функция (Рис-2)

ад

I zo I----------------------- о                   t

(Рис-2)

*         1

• 1.3.    Если k <  0 , то функция (5) убывает и в момент времени t = — k

• 2.    Пусть будет а >  в .

  • 2.1.    Если k > 0 , то функция (5) в момент времени

• 2.2.    Если к <  0, то функция (5) монотонно убывает, и эта функция обращается в ноль со временем T , как в случае 2.1 (Рис-5).

  

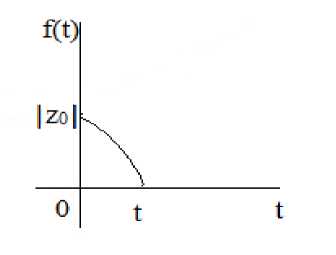
  (Рис-5)

  
  

  2.3. Если k = 0, то

  
  

  f ( t , a , k , a , в ) =

  
  

  a - — (a — в ) и время преследования

  
  

  равно T _o =

  
  

  2 z о

  a — в

  
  

равна нулю (Рис-3)

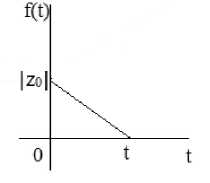
(Рис-3)

T = (| z₀|k + ^| z ₀1² к ² + 2 | z ₀ |( а - в ) ) / (а - в) равна нулю (Рис-4)

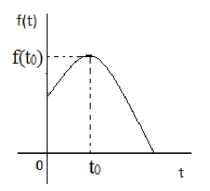
(Рис-4)

Максимальное значение функции (5) в момент t0 = |z0|k / (а — в),будет равно следующему:

f ( t о ) = ( 2| z о| ( а — в ) +| z о|² к ²) /2( а — в ) .

Следовательно, соотношение (3) верно в какой-то момент t * на основании неравенства | z ( t )| < | z ₀1 ( kt + 1) + 1 ² ( в — a ) / 2 и свойства (5), и определяется, что соотношение t * <  T является правильным, т.е. задача преследования решена, что завершает доказательство теоремы.