Конформно-плоская открытая модель вселенной с произвольной функцией состояния

Найденное А.Фридманом решение уравнений Эйнштейна для открытой модели Вселенной [1] еще не охватывает всех возможных такого рода решений космологических уравнений для изотропного пространства отрицательной кривизны. Это решение является исходным для обсуждения космологических моделей и имеет уравнение состояния некогерентной пыли, то есть в нем отсутствует давление. Можно было бы сказать, что фридмановская модель заполнена веществом в приближении идеальной жидкости с нулевым давлением. При этом, решение А.Фридмана относится к конформно-плоским решениям, для которых конформный тензор кривизны Вейля (см., например, [2]) равен нулю, что предполагает запись метрики в конформно-плоском виде для четырехмерного пространства-времени. Однако зачастую метрику этого решения записывают в синхронных координатах (см., например, [3]), несмотря на трудности, связанные как с анализом решения для пылевидной материи, записанного в параметрическом виде, так и с другими уравнениями состояния при рассмотрении обобщений модели Фридмана.

С другой стороны, подавляющее большинство космологических моделей, основанных на точных решениях уравнений Эйнштейна, получено а предположении, что уравнение состояния вещества, то есть связь между плотностью энергии и давлением, в модели есть величина постоянная. Очевидно, что динамическая модель Вселенной должна содержать фукциональное уравнение состояния. Другими словами, уравнение состояния вещества в этом случае должно быть функцией точки пространственно-временного континуума или функцией состояния.

Кроме того, В.Фок предложил подход ( [4]- [5]) к описанию открытой фридмановской модели, связанный с введением конформной метрики метрике Минковского четырехмерного пространства-времени, то есть конформно-плоской или конформно-галилеевой метрики. При этом им были указаны преобразования, связывающие такую запись метрики с записью в синхронной системе отсчета. Оказывается, как показано в [6], эти преобразования эквивалентны переходу от синхронной системы отсчета к кинеметрической ( [7]- [13]). Далее, при обобщении решения Фридмана на случай наличия равновесного светоподобного излучения (подобного электромагнитному) в ( [14]- [15]) был использован подход В.Фока для нахождения точного космологического решения с излучением и тензором энергии-импульса в приближении идеальной жидкости с отличным от нуля давлением без введения конкретного уравнения состояния. Анализ функции состояния для этого случая выявил катастрофическое поведение космологической модели в зависимости от параметра, связанного с плотностью вещества. Согласно теории катастроф (см., например, [16]) такое поведение физической системы описывается катастрофой сборки и является аналогом фазового перехода второго рода в конденсированных средах. В дальнейших работах ( [17]- [20]) применение данного подхода было продолжено, а в [21] для описания открытой космологической модели были еще использованы функции Бесселя полуцелого порядка, что позволило получить решение ( [14]- [15]) как частное. Следующее обобщение решения Фридмана на случай наличия как излучения, так и вязкости среды было найдено в ( [22]- [23]).

1.    Уравнения гравитационного поля для открытой космологической модели

Упомянутый выше подход В.Фока ( [4]- [5]) для описания открытых космологических моделей основан на записи 4-метрики пространства-времени в следующем виде:

ds2 = ехр(2о)8н" dx*dx",

(1.1)

где¹ exp(2o) — кош] ) ор\шни множитель ： а = o(S); S² = 8 丛“ x^Mx^v = t²—r²; 8 丛“ = diag(1 ； —1; —1; —1) —метрический тензор Минковского; 〃， v = 0 , 1 , 2 , 3; скорость света и гравитационная постоянная Ньютона равны единице, поэтому эйнштейновская гравитационная постоянная здесь равна к = 8n.

Перейдем к рассмотрению системы уравнений Эйнштейна

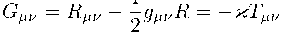
(1-2)

с тензором энергии-импульса в приближении идеальной жидкости (ТЭИ)

T^v = fuHuv + pbpv,

(1.3)

где¹ £ — плотность 'Әпергіш ： p — давление ： 4-скорость u* = exp ( o)b^ пропорциональна градиенту перемеішоп S как (функции координат x* : b* = S,/ u^U = 1 - условие нормировки 4-скоростп ： b*v = u*uv — g*v есть 3-проектор на 3-пространство, который играет роль метрпчсч?кого тензора для 3-пространства, при этом выполняется условие ортогональности 3-пространства и временноподобной конгруэнции и* : b*vu* = 0.

Воспользовавшись монадным формализмом ( [7]- [13]) и проведя (1+3)-расщепление системы (1.2) путем проектирования ее на временноподобную мировую линию и пространственноподобную поверхность, ортогональную временноподобному направлению, получим два уравнения:

³(² ( + ⑺ 2)

к£ • exp(2a);

(1-4)

² 化 + ^ +

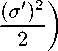
— кр • exp(2a),

(1.5)

где роль монады выполняет вектор 4-скорости u*; штрих обозначает производную по переменной S.

В итоге, при таком (1+3)-расщеплении пришли к двум уравнениям: одно определяет плотность энергии, а другое - давление.

2.    Функция состояния

Прежде чем интегрировать полученную систему уравнений (1.4)—(1.5) введем функцию состояния

^e(S )= 需

(2.1)

на которую можно наложить условие | e(S) | 工 1, если потребовать выполнения энергодоминатио-С 工口: £(S) >  p(S).

Функцию состояния (2.1) для каждого фиксированного значения S можно рассматривать как «мгновенное» уравнение состояния, с одной стороны, а, с другой, на тех промежутках значений переметшоіі S, где¹ nj) он сходит до ( ?та.то^т-и ю медленное п плавное изменение e(S), можно вводить уравнения состояний, то есть конкретные физически интерпретируемые соотношения между плотностью энергии f(S) и давлением p(S).

После умножения уравнения (1.4) на функцию состояния e(S) сложим его с уравнением (1.5). В результате получим

N + 1 /(2 + 3в (S)) + 1 5)2(1 + 3e(S)) = 0.

(2.2)

S2

Вводя ： зам ( ?иы Z = d ii £(S) = (1 + 3/(S)), сведем (2.2) к уравненшо Риккати.

Z = E(S) U(S)

E(S) = exp

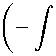
C exp S

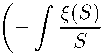
dS

C

S2 exp

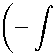
学 ds)

ii C = const.

Интегрирование (2.5) позволяет получить

U (S)

И

Z (S) = / = U (S) E(S)

ИЛИ

b(S) = -2 /

exp

C1+C2

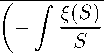
dS

C

S exp

Ci + C exp

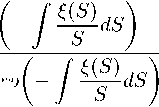
C

S2 exp

(-/3T dS)

C

Ci + 2SexP

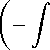
3 e(S)

S

2Ci + Cexp

C

S2 exp

中 d$)

\dS + C2, 学 dS)

(2.3)

(2.4)

(2.5)

(2.6)

(2.7)

(2-8)

(2-9)

rj,e C2 - постоянная ііігтстрііроваішя.

Полученное решение для показателя степени конформного множителя необходимо «откалибровать», то есть выбрать постоянные интегрирования C, Ci, C2 такими, чтобы при стремлении переметшоіі S т х коіі(})ормііып множитель exp(2 o(S)) стремился к ретеншо Фридмана для открытой модели Вселенной в форме Фока exp(2^F)

(1 -)

⑵ 10)

rje A постоянная из решения Фридмана . связатшая с палпчік?м в модели веш,ества (A > 0).

Другими словами, на полученное решение (2.9) накладывается физическое требование: при расширении открытая космологическая модель должна проходить через фридмановскую стадию иекогереіітііой пыли, то есть через стадию с в = 0. Кроме того, в пределе S = х пространство-время должно быть плоским, то есть метрика должна совпадать с метрикой Минковского.

Эти требования удовлетворяются при следующем выборе постоянных: C = -A; Ci = 1/2; C2 = 0, ii окончательно получаем с л еду тонн ііі обшіпі вид показателя степени коіі ( } ) ормііого множителя для произвольной функции состояния e(S):

b(S)

S2 • exp (^-3/ 乎 ^dS)

1-

A

S exp

(-3/ 手 dS)

dS.

(2.11)

Как уже упоминалось выше, открытая модель Фридмана описывается уравнением состояния иекогереіітііой пыли p = 0 (e(S) = 0), которое является частным случаем линейного уравнения состояния, нередко используемого в физике,

p(S)= во • e(S),                                        (2.12)

c | во | 工 1 ； во = const.

В частности, для целых положительных значений n = 3(1 + во) выражение (2.11) легко интегрируется, и в результате находим

b(^S) = —2^ In f¹ - QA^= —23 ^ln(y^(S)). n — 2 \   Sⁿ 2/ n — 2

⑵ 13)

(2.14)

⑵ 15)

Отсюда видно, что функция

y(S)= 1 —白， которая связана с конформным множителем как

(4/n—2)

exp(2o(S)) = y(S)(4/n-2) = (1 — S—\ представляет собой гармоническую функцию, удовлетворяющую уравнению Лапласа для «сферически симметричного» случая в пространстве размерности n, к которому сводится уравнение (2-2),

■ dS(S^{(n — х)} dy) = y 〃 +F y ， = ⁰ ・ ⑵⑹

Другими словами, космологические уравнения (1.4)-(1.5) для такого выбора уравнения состояния могут быть сведены к многомерному уравнению Лапласа. При этом оказывается, что корень четвертой степени из решения Фридмана (2.10) есть гармоническая функция у = 1 — A/S для n = 3, а давление из (1.5) тождественно равно иулто для такой (функции у.

Рассмотрение открытых космологических моделей с линейным уравнением состояния и их связь с гармоническими функциями было предпринято в работах ( [24]- [27]). В работах [28]- [29] сделана попытка использовать выражение (2.11).

3.    Заключение

В работе рассмотрена открытая космологическая модель, заполненная материей в приближении идеальной жидкости в общем случае с отличным от нуля давлением. Соответствующая 4-метрика записана в форме Фока как конформная метрике Минковского и зависит только от одной переменной, квадрат которой представляет собой произведение запаздывающего и опережающего времен. Известное решение Фридмана для открытой Вселенной, заполненной некогерентной пылью, является частным случаем для такой метрики.

С помощью монадного формализма уравнения Эйнштейна расщепляются на два уравнения. Затем эта система решается в общем случае для произвольной функции состояния. Полученное решение в виде квадратуры калибруется относительно решения Фридмана. Такую запись легко использовать в численном моделировании различных сценариев динамики моделей открытой Вселенной. Ограничиваясь линейным уравнением состояния, приходим к ранее полученным результатам по введению гармонических функций для описания открытой Вселенной.