Конкурентное сходство как универсальный базовый инструмент когнитивного анализа данных

Когнитивный анализ данных направлен на изучение методов, с помощью которых человек извлекает закономерности из информации об окружающем мире и затем использует их для получения новых знаний, для более эффективного принятия решений. Эти исследования служат основой для построения компьютерных систем анализа данных, которые, имитируя простейшие когнитивные способности человека, позволяют решать задачи больших объемов, извлекать закономерности тогда, когда человеческих ресурсов на это не хватает. Ярким примером такой задачи могут служить результаты микрочипирования (microarrays) – технологии измерения активности большого количества генов одновременно, которая активно развивается, в том числе, в связи с задачей установления связей между различными заболеваниями и особенностями функционирования генома пациента. Результатом таких исследований становятся таблицы, содержащие информацию о сотнях пациентов и десятках тысяч генов, обработать которые вручную не представляется возможным.

Анализ данных, как направление кибернетики, начал активно развиваться с середины прошлого века, а в связи с появлением компьютеров и непрерывным ростом их мощностей стал неотъемлемой частью исследований в самых разных областях медицины, биологии, геологии, социологии, экономики и пр. У истоков этого направления наряду с такими учёными как С.А. Айвазян [1], Э.М. Браверманн [2], В.Н. Вапник [3], Ю.И. Журавлев [4],

А.Г. Ивахненко [5], М.И. Шлезингер [6] стоял и Николай Григорьевич Загоруйко [7-9], заслуги которого, как учёного и популяризатора анализа данных, сложно переоценить.

Благодаря усилиям большого количества исследователей к настоящему времени в области анализа данных разработано огромное количество разных методов решения одних и тех же задач. Создаются всё новые и новые методы, ориентированные отдельно на большие и малые выборки, на тот или иной закон распределения, на два образа или на большее их число, на линейно или нелинейно разделимые образы и т. д. Подобное многообразие можно объяснить различием моделей, в рамках которых каждый исследователь формулирует и решает ту или иную задачу анализа данных. Причём высокая специфичность модели, несмотря на точность и математическую обоснованность решений, получаемых в ней, может приводить к тому, что для большинства реальных прикладных задач она не будет работать.

Идея, которую Н.Г. Загоруйко продвигал в последние годы работы, заключалась в том, что модель для решения различных задач анализа данных должна быть универсальной, отражать человеческую способность обработки информации и благодаря этому успешно способствовать решению задачи, которые может ставить человек. Он исходил из гипотезы о том, что когнитивные способности человека основаны на двух ключевых принципах: на использовании специфической меры сходства между объектами и на стремлении к максимальной компактности и простоте описания мира в терминах этой меры сходства. В качестве модели человеческого способа оценки сходства между объектами он предложил использовать функцию конкурентного сходства (FRiS-функцию, от Function of Rival Similarity ) [10]. Использование FRiS-функции позволяет найти количественную оценку компактности классов. Эти два элемента – FRiS-сходство и FRiS-компактность лежат в основе алгоритмов для решения различных типов задач анализа данных. Примеры их успешного использования для решения прикладных задач самой разной природы подтверждают работоспособность модели конкурентного сходства.

1    Функция конкурентного сходства. Алгоритм FRiS-Stolp

При измерении таких характеристик объектов, как вес, длина, сопротивление и т.п., обычно используются эталонные объекты. Результат измерения определяется свойствами только самого объекта и измеряющего эталона и не зависит от свойств других объектов . По этой причине он имеет характер абсолютной величины. Но объекты описываются и такими характеристиками, как «похож–не похож», «близок–далёк», «добрый–злой» и т.д. Эталонов для подобных понятий не существует, два объекта с несовпадающими свойствами могут считаться «сходными» или «не сходными», «близкими» или «далёкими» в зависимости от свойств других объектов . Так, на рисунке 1 расстояние между объектами а и z остается неизменным, но ответы на вопрос «достаточно ли они близки друг к другу, чтобы можно было объединить их в один класс?» для случаев 1, 2, и 3 будут разными.

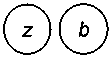
Рисунок 1 – Иллюстрация относительности сходства объектов a и z

Чтобы ответить на этот вопрос, нужно знать ответ на вопрос «по сравнению с чем?». Хорошо известная бытовая фраза «всё познается в сравнении» на самом деле отражает фундаментальный закон познания. Адекватная мера сходства должна определять величину сходства, зависящую от особенностей конкурентного окружения объекта z. При распознавании принадлежности объекта z к одному из двух образов A или B важно знать не только его расстояние до образа А , но и расстояние до конкурирующего образа В . Следовательно, сходство в распознавании образов является категорией не абсолютной, а относительной.

Все статистические алгоритмы распознавания учитывают конкуренцию между классами. Например, в методе kNN (k-Nearest Neighbors¹) новый объект z распознаётся как объект образа А , если среднее расстояние до k ближайших объектов этого образа не только мало, но и меньше, чем среднее расстояние до k ближайших объектов конкурирующего образа В . Оценка сходства в этом алгоритме делается в шкале порядка.

Более сложная мера сходства используется в алгоритме RELIEF [11]. Чтобы определить сходство объекта z с ближайшим объектом a из образа А в конкуренции с ближайшим объектом b из образа В используется величина, которая учитывает нормированную разницу в расстояниях r ( z, a ) и r ( z, b ):

_{W ( z , a | b )}    r ( z , b ) r ( z , a ) .

г — г max min

Здесь r min и r max – минимальное и максимальное расстояния между всеми парами объектов анализируемого множества.

В работе [12] при оценке «Ширины Силуэта» (Silhouette Width) измеряется среднее расстояние R ( z, A ) от объекта z до всех объектов образа A , к которому относят z , и расстояние r ( z, b ) от z до ближайшего к нему объекта b , не принадлежащему образу А. Мера различия (несходства) объекта z и объектов кластера А принимается равной

_{S ( z , A | b )}       R ( z , A ) r ( z , b )    .

max{ R ( z , A ), r ( z , b )}

Для вычисления конкурентного сходства объекта z с объектом a в конкуренции с ближайшим объектом b предлагается использовать следующую величину:

r ( z , b ) r ( z , a )

F ( z , a | b )                       .

r ( z , b ) r ( z , a )

По мере передвижения объекта z от объекта а к объекту b можно говорить вначале о большом сходстве объекта z с объектом а , об умеренном их сходстве, затем о наступлении одинакового сходства, равного 0, как с объектом а , так и с b . При дальнейшем продвижении z к b возникает умеренное, а затем и большое отличие z от а. Совпадение объекта z с объектом b означает максимальное отличие z от а , что соответствует сходству z с a , равному -1.

Сходство F между объектами не зависит от положения начала координат, поворота координатных осей и одновременного умножения их значений на одну и ту же величину. Но независимые изменения масштабов разных координат меняют вклад, вносимый отдельными характеристиками в оценку и расстояния, и сходства. Так что сходство между объектами зависит от того, с какими весами учитываются разные характеристики. Меняя веса характеристик, можно подчеркнуть сходство или различие между заданными объектами, что обычно и делается при выборе информативных признаков и построении решающих правил в распознавании образов.

Конкурентное сходство объектов с образами будем определять по тому же принципу, что и конкурентное сходство объектов с объектами:

_{F ( z , A | B )}    r ( z , B )   r ( z , A ) .

r ( z , B )   r ( z , A )

При этом расстояние от объекта z до образов A и B может вычисляться по-разному. В качестве него может использоваться и расстояние r ( z, a ) до ближайшего объекта a образа A , и среднее расстояние до всех объектов образа, и среднее расстояние до k ближайших объектов образа, и расстояние до центра тяжести образа и т.п. В дальнейшем, в качестве расстояния от объекта до образа по умолчанию будет использоваться расстояние до ближайшего объекта этого образа.

Сходство в шкале порядка, используемое в методе kNN, отвечает на вопрос «на объекты какого образа объект z похож больше всего?». Конкурентное сходство, измеряемое с помощью FRiS-функции, отвечает на этот вопрос и, кроме того, на вопрос «какова абсолютная величина сходства z с образом А в конкуренции с образом В ?». Оказалось, что дополнительная информация, которую даёт абсолютная шкала по сравнению со шкалой порядка, позволяет существенно улучшить методы анализа данных.

В таблице 1 приводится сравнение различных критериев для выбора информативных признаков. FRiS-критерий сравнивался с такими критериями выбора признаков как, Silhouette Width (SW), ошибка скользящего контроля по правилу ближайшего соседа (NN), критерий Фишерa (Fisher) и RELIEF. Сравнение осуществлялось на двух сериях выборок. В первом случае образы были представлены нормальными распределениями, искусственно «испорченными» добавлением зашумленных и случайных признаков (V1). Во втором случае образы изначально имели сложную полимодальную структуру, которая маскировалась добавлением зашумлённых и случайных признаков (V2). Решалась задача выбора информативной подсистемы признаков. Для оценки эффективности того или иного критерия использовалась надёжность распознавания тестовой выборки в выбранном с помощью критерия признаковом пространстве.

Таблица 1 – Сравнение различных критериев для выбора информативных признаков

	V1			V2
\N	50	100	150	50	100	150
FRiS	0.930308	0.938042	0.939497	0.818071	0.856152	0.866458
SW	0.924218	0.937614	0.943244	0.655248	0.690778	0.702515
NN	0.895255	0.894467	0.906625	0.735635	0.772785	0.80093
Fisher	0.935972	0.943948	0.942755	0.598515	0.60059	0.605303
RELIEF	0.899302	0.932148	0.930718	0.710267	0.754834	0.791442

Анализ представленных результатов позволяет заключить, что если в простых случаях унимодальных образов с небольшой зоной пересечения все критерии работают примерно одинаково, то в случае сложных полимодальных структур FRiS-критерий значительно опережает другие критерии.

Одним из способов проявить особенности данных в задаче распознавания является переход к их сжатому описанию с помощью множества эталонных представителей каждого образа, сохраняющему основные закономерности, необходимые для хорошего распознавания как объектов исходной выборки, так и новых объектов. Такие эталонные объекты будем называть столпами. Чем сложнее структура образов, чем сильнее они пересекаются, тем больше столпов потребуется для описания таких данных. Если удастся построить такое описание данных и перейти от образов A и B к множествам столпов этих образов SA и SB, соответст- венно, то вычислять конкурентное сходство объекта z с образом A в конкуренции с образом B можно как F(z, SA|SB). Вычисление конкурентного сходства не по всей выборке, а по её сжатому описанию позволяет адаптировать данную меру к особенностям решаемой задачи.

Для построения сжатого описания данных в виде системы столпов используется алгоритм FRiS-Stolp [13]. Алгоритм работает при любом соотношении количества объектов к количеству признаков и при произвольном виде распределения образов. В качестве столпов выбираются объекты, которые обладают высокими значениями двух свойств: обороноспособности по отношению к объектам своего образа и толерантности по отношению к объектам других образов. Чем выше обороноспособность эталона, тем меньше будет ошибок первого рода (пропуск цели). Чем выше толерантность эталона, тем меньше будет ошибок второго рода (ложная тревога). Набор столпов считается достаточным для описания выборки, если сходство F всех объектов обучающей выборки с ближайшими своими столпами в конкуренции с ближайшими объектами других образов превышает пороговое значение F *, например, F * = 0.

Отметим некоторые особенности алгоритма FRiS-Stolp. Вне зависимости от вида распределения обучающей выборки столпами выбираются объекты, расположенные в центрах локальных сгустков и защищающие максимально возможное количество объектов с заданной надёжностью. При нормальных распределениях столпами в первую очередь будут выбраны объекты, ближайшие к точкам математического ожидания. Следовательно, при приближении закона распределения к нормальному, решение задачи построения решающих функций стремится к статистически оптимальному. Если распределения полимодальны и образы линейно неразделимы, столпы будут стоять в центрах мод. Сжатое описание образов через множество столпов также можно использовать для распознавания новых объектов.

2  FRiS-компактность. Алгоритм FRiS-GRAD

Практически все алгоритмы распознавания в том или ином виде основаны на использовании гипотезы компактности. При этом в зависимости от модели образы признаются компактными при выполнении одного из нижеперечисленных условий: если они имеют простую форму, разделяются границей простой формы, объекты одного образа похожи друг на друга и не похожи на объекты других образов. Для получения количественной оценки компактности каждого образа в отдельности и качества (информативности) признакового пространства предлагается использовать описанную выше FRiS-функцию, формализующую представление о компактности образа, в соответствии с которым «внутреннее» сходство его объектов друг с другом велико, а «внешнее» сходство с объектами других образов мало.

Действительно, для произвольного объекта a A мера конкурентного сходства этого объекта со своим образом в конкуренции с образом B показывает, насколько этот объект похож на свой образ и не похож на образ B . Если эта величина для всех объектов образа А положительна, то можно считать данный образ компактным. Таким образом, вычисляя среднее значение FRiS-функции по всем объектам образа A , можно оценить компактность данного образа. Если при этом вычислять FRiS-функцию с опорой на столпы, то такая оценка компактности будет автоматически адаптироваться к особенностям данных.

Более формально процедура вычисления компактности для случая двух образов выглядит следующим образом.

• 1)    С помощью алгоритма FRiS-Stolp строятся множества столпов S A и S B образов A и B .

• 2)    Для каждого элемента a A оценивается сходство с ближайшим столпом из множества S A в конкуренции с ближайшим столпом из S B . Затем вычисляется FRiS-компактность образа A в конкуренции с образом B :

' ■ ТТЛ F ( a • ^sa\^s b )" S a I) -

SA A a A

Отметим, что количество столпов образа зависит от структуры распределения объектов и величины порога F *: с ростом F * увеличивается как число столпов, так и точность описания распределения, но растёт и сложность его описания, т. е. множитель 1 / | S_A| является штрафом за структурную сложность образа.

• 3)    Аналогично вычисляется величина C BA FRiS-компактности образа B в конкуренции с A . 4) Далее получим оценку компактности образов A и B как усреднение величин C_A|B и C_B|A :

С = C a | в + С в a -

Умение оценивать компактность выборки полезно для нахождения информативной подсистемы признаков, так как величина компактности может использоваться как критерий качества набора признаков. В настоящее время преобладают задачи, в которых количество признаков N на порядки превышает количество объектов M . При этом информация, полезная для решения конкретной классификационной задачи, обычно представлена в нескольких признаках n << N . Выбор этих n признаков позволяет в дальнейшем не только существенно сократить затраты машинных ресурсов, но и повышает надёжность распознавания образов. Признаки могут зависеть друг от друга, что не позволяет по оценкам индивидуальной информативности каждого признака выбрать подмножество в виде списка из n наиболее информативных признаков. Если n задано, точное решение можно получить, проверив все сочетания из N признаков по n , что в реальных задачах часто практически невозможно. По этой причине используются эвристические алгоритмы направленного перебора, например, алгоритмы AdDel [7] или GRAD [8].

Величина FRiS-компактности используется в качестве критерия информативности в алгоритме выбора признаков FRiS-GRAD [14]. Данный критерий применим к любому виду распределений и любому соотношению M и N . Так как для вычисления FRiS-компактности требуется строить систему столпов, описывающую выборку в каждом из рассматриваемых подпространств, то можно считать, что алгоритм FRiS-GRAD формирует не только набор информативных признаков, но и решающее правило, представленное в виде системы столпов.

Для оценки эффективности алгоритма FRiS-GRAD проводилось его масштабное тестирование на девяти медицинских задачах, объектами в которых выступали пациенты с различными заболеваниями, а признаками — экспрессия генов, полученная с помощью микрочипирования. Особенностью этих задач была их плохая обусловленность, а именно: число признаков на несколько порядков превышало число объектов в выборке.

Результаты работы алгоритма сравнивались с более ранними результатами, полученными четырьмя наиболее часто используемыми алгоритмами распознавания (метод опорных векторов, межгрупповой анализ, байесовский классификатор и метод к ближайших соседей) в информативных подпространствах, выбранных десятью известными алгоритмами выбора признаков.

Для оценки качества работы алгоритмов использовалась перекрёстная проверка: 50% выборки использовалось для обучения, а на оставшихся 50% оценивалась надёжность распознавания. Все результаты (кроме относящихся к FRiS-GRAD) были взяты из [15], где для каждой задачи приводилось 40 различных вариантов решений, полученных всеми возможными сочетаниями алгоритмов. Для сравнения были выбраны лучшие результаты по каждой задаче. Результаты сравнения представлены в таблице 2. Здесь показаны: имя задачи, размерность признакового пространства N, отношение количества объектов первого образа M1 к количеству объектов второго образа M2 и два столбца результатов - ожидаемая надёжность распознавания для лучшего сочетания алгоритмов и ожидаемая надёжность распознавания для алгоритма FRiS-GRAD.

Таблица 2 - Результаты решения девяти задач

Задачи	N	M 1/ M 2	Рекорды	FRiS-GRAD
ALL1	12625	95/33	100.0	100.0
ALL2	12625	24/101	78.2	93.7
ALL3	12625	65/35	59.1	75.3
ALL4	12625	26/67	82.1	93.7
Prostate	12625	50/53	90.2	94.1
Myeloma	12625	36/137	82.9	93.9
ALL/AML	7129	47/25	95.9	100.0
DLBCL	7129	58/19	94.3	96.0
Colon	2000	22/40	88.6	94.2
Average			85.7	93.4

Анализ представленных результатов показывает уверенное превосходство алгоритма FRiS-GRAD перед наиболее популярными алгоритмами анализа данных при решении сложных, плохо обусловленных задач, в которых количество признаков на порядки превосходит количество объектов в выборке.

3    Оценка разделимости классов. Алгоритм FRiS-Censor

Алгоритм FRiS-Stolp наращивает количество столпов до тех пор, пока все объекты не станут надёжно защищенными. Надёжно защищённым считается объект, сходство которого с ближайшим столпом своего образа в конкуренции со столпами образа-конкурента превышает заданный порог F *. Каждый столп с множеством надёжно защищаемых им объектов образует кластер. Но на последних шагах работы алгоритма возникают столпы, которые защищают малые количества объектов, вплоть до того, что они защищают только самих себя. На роль таких столпов могут попасть «шумовые» объекты (выбросы), свойства которых сильно отличаются от свойств остальных объектов образа. Иногда это говорит об уникальных свойствах таких объектов, однако, более часто причина отличий состоит во влиянии неучитываемых факторов, таких как сбой измерительных приборов, ошибки занесения данных в протокол и пр. Встречаются и объекты, которые не являются «ошибочными», но находятся на периферии распределения и оказываются глубоко в зоне пересечения с соседним образом. Они тоже могут неоправданно сильно усложнить решающие правила, делая их «вычурными». Таким образом, «погоня» за мелкими и единичными кластерами ведёт к переобучению.

Качество описания обучающей выборки (или оценка разделимости классов) зависит от набора выбранных эталонов. В случае, когда каждый объект выборки является столпом, информация о ней сохраняется полностью, но для распознавания такое описание не пригодно. О том, насколько хорошо некоторая система столпов описывает классы в заданном признаковом пространстве, будем судить по оценке качества описания обучающей выборки, опирающейся на понятие компактности.

В случае двух классов для каждого элемента обучающей выборки оценивается его сходство с ближайшим столпом своего образа в конкуренции с ближайшим объектом из конкурирующего образа и затем вычисляется качество описания обучающей выборки L столпами:

H ( L ) ¹ F ( a , S A | B ) F ( b , S B | A ) .

S_A S_B A B a A ^A b B ^B

При изменении количества столпов L меняется качество описания H обучающей выборки и ошибка распознавания E тестовой выборки. Выдвигается и проверяется гипотеза о том, что между функциями H ( L ) и E ( L ) имеется закономерная связь, используя которую можно найти такое количество столпов, что дальнейшее увеличение числа столпов ведёт к переобучению.

Проверка этой гипотезы проводилась на модельной задаче распознавания двух образов, каждый из которых представлял собой суперпозицию нескольких (от 2-х до 4-х) нормально распределённых кластеров в двумерном пространстве признаков. Рассматривалось 10 распределений, которые отличались друг от друга количеством образующих нормальных компонентов, их дисперсиями, координатами математических ожиданий и количеством объектов в компонентах. Каждый образ был представлен 250 объектами. При каждом распределении выборка 100 раз случайным способом делилась на две части: обучающую (по 50 объектов первого и второго образов) и контрольную (по 200 объектов каждого образа). Количество экспериментов при различных численных реализациях исходных данных было равно 1000.

Результаты отдельных экспериментов, приведенные на рисунке 2, служат подтверждением выдвинутого предположения. Таким образом, сформулирована и экспериментально подтверждена гипотеза о том, что точка перегиба кривой (первый локальный максимум функции H ), описывающей разделимость классов, может служить сигналом о начале переобучения. Объекты, оставшиеся незащищёнными, считались выбросами и исключались из рассмотрения.

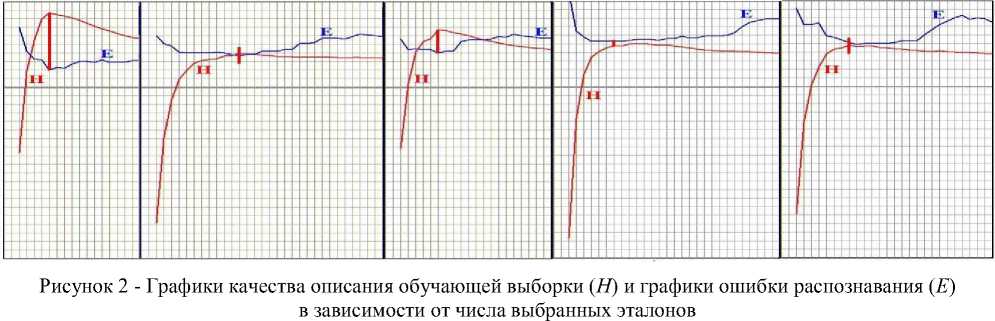
Алгоритм FRiS-Censor [16], отыскивающий эту точку перегиба, позволил улучшить качество распознавания в сравнении со стандартным алгоритмом FRiS-Stolp на 3-5%. При этом число столпов, достаточных для описания выборки, снижалось в среднем в 3 раза относительно числа столпов, достаточных для защиты всех объектов выборки.

Заключение

Функция конкурентного сходства оказалась универсальным инструментом для разработки алгоритмов решения различных типов задач когнитивного анализа данных. Наиболее интересные и убедительные результаты работоспособности этой модели были получены для задачи выбора информативной системы признаков в случае плохо обусловленных задач сложной структуры. Помимо задач, описанных выше, с её помощью удалось решить задачу таксономии (алгоритм FRiS-Tax [17]), задачу частичного обучения (алгоритм FRiS-TDR [18]), задачу заполнения пробелов в двух- и трёхмерных таблицах данных (FRiS-ZET и 3D-ZET [19]). Все эти алгоритмы показали свою эффективность и активно используются для решения прикладных задач в самых разных областях.

Достижение таких результатов было бы невозможным без светлых идей и чуткого руководства Загоруйко Николая Григорьевича. Мы благодарны судьбе за возможность работать с этим удивительно талантливым и мудрым человеком. Светлая ему память.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 14-01-00039.