Консервативная оценка функционирования узла обтюрации газодинамической импульсной системы на базе статистического подхода

EDN MYHXAK

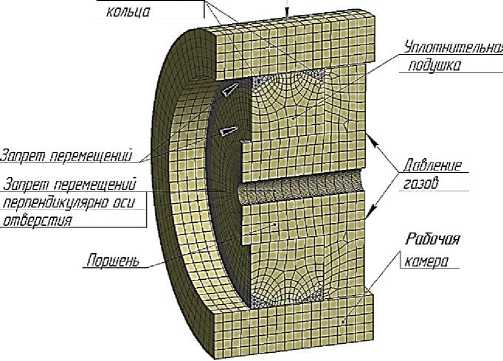
Одной из основных задач, решаемых при создании газодинамической импульсной системы (ГИС), является обеспечение герметизации рабочей камеры [1]. То есть, предотвращение прорыва продуктов горения топлива (ПГ) через узел обтюрации, запирающий рабочую камеру. На рисунке 1 приведена схема герметизации рабочей камеры ГИС, где изображены элементы обтюрирующего узла, предотвращающего прорыв ПГ, находящихся под давлением Р между камерой и штоком, посредством плотного прилегания эластичной подушки к уплотнительному участку камеры и штоку. Конструкция узла обтюрации, как правило, представляет собой эластичную уплотнительную подушку, выполненную из гиперупругих полимерных материалов в форме цилиндра или усечённого конуса. Спереди и сзади подушки устанавливаются металлические кольца (Рисунок 1). Кольца большего диаметра могут иметь косой разрез, позволяющий ему упруго деформироваться в тангенциальном направлении, скользя по конической поверхности камеры, плотно к ней прилегая и обеспечивая обтюрацию ПГ.

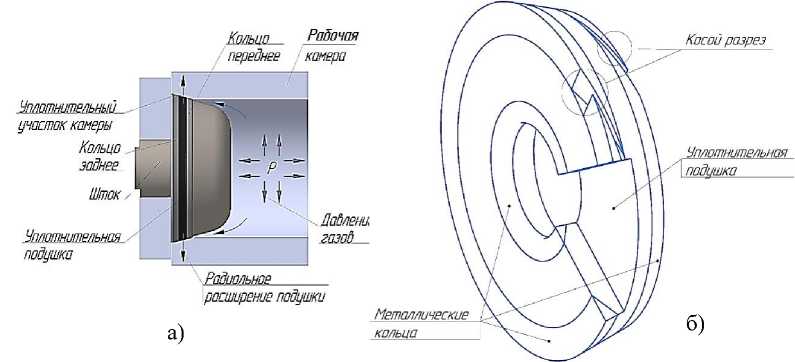
Рисунок 1 – Элементы газодинамической импульсной системы : а) – схема герметизации камеры; б) - конструкция узла обтюрирации

Особенности функционирования узла обтюрации обусловлены нестабильностями процессов, происходящих при работе ГИС. При этом на оценку функционирования узла обтюрации оказывает неопределенность физико-механических свойств его элементов, изготавливаемых из различных материалов, как из эластичных, так и высокопрочных, выдерживающих предельно-высокие нагрузки. Значение имеют также разбросы геометрии элементов в пределах допусков на их изготовление. С учетом указанных особенностей расчетная оценка функционирования узла обтюрации на основе детерминистского подхода оказывается нецелесообразной. Это приводит к необходимости проведения натурных испытаний на каждом изделии после его изготовления и их выбраковки по результатам этих испытаний.

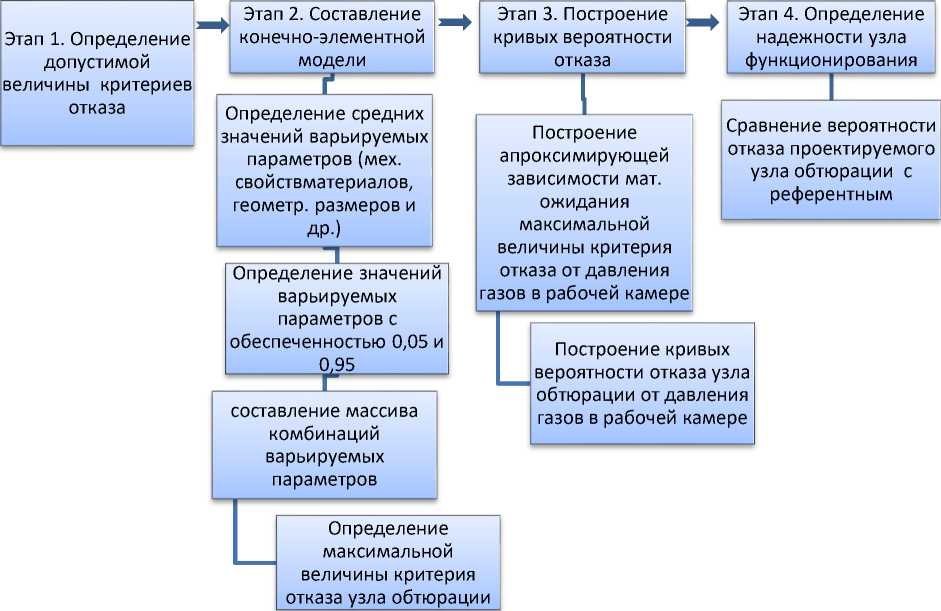
В данной работе рассмотрен статистический подход к расчетной оценке функционирования узла обтюрации ГИС, основанный на оценке надежности функционирования. За основной кри-терией надежности узлов обтюрации принимается их работоспособность – способность узла обтюрации герметизировать камеру от прорыва ПГ с вероятностью не менее заданной. В основу раз- работанного подхода положено построение кривых вероятности отказа узла обтюрации в зависимости от давления ПГ и их оценка с учетом неопределенности различного рода, вносимых элементами узла обтюрации и процессами, происходящими при функционировании ГИУ. В качестве входных параметров расчетной модели принимаются стохастические данные, полученные при интерполяции неизвестной функции нескольких переменных. Это дает возможность разработать расчетную модель, позволяющую оценивать вероятность достижения предельного состояния для неизвестной, в общем случае, функции отклика на нагрузку Q (напряжения, деформации, перемещения и т.п.), которая зависит от ряда параметров геометрии, механических характеристик, погрешности расчетной модели и пр., а также оценивать влияние (чувствительность) входных параметров модели на результирующее значение вероятности отказа, оптимизировать время расчетов. С целью оценки параметров распределения функции Q используется разложение в ряд Тейлора до второго порядка малости, что в ряде случаев может дать достаточную консервативную оценку искомого результата.

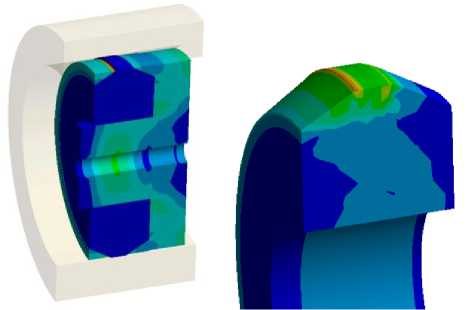
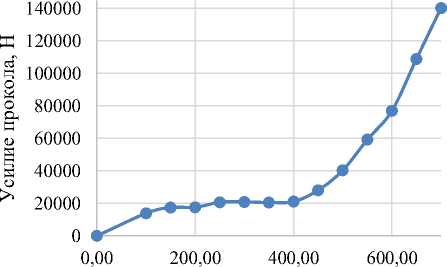
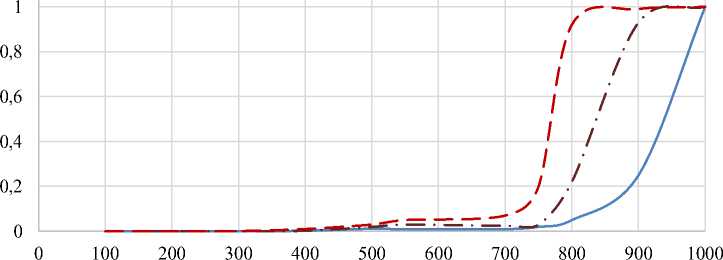
P(R

Общие положения

Разработанный подход подробно описан в [2].

Пусть имеется ответная реакция на нагружение Q. Вероятность того, что характеристика предельного состояния (критерии по напряжениям, деформациям и т. д.) окажется меньше R P(R < Q), т.е. наступит разрушение будет [3]:

Q

P(R < Q) = F_R(Q) = fp_R(z)dz,      (1)

-ГО где    Fr(Q~) - функция распределения случай ной величины R;

p_R(z) - плотность распределения величины R.

Для нахождения вероятности разрушения следует учесть все возможные значения Q (все несовместимые пути реализации события) по формуле полной вероятности со

PQ(Q)FR(Q)dQ =

-ГО ГО

= 1- ^ PR(R)FQ(R)dR.  (2)

-ГО

Построение плотности распределения параметра прочности

В действующих нормативных документах и справочниках значения величин, характеризующих прочность материала представлены, как правило, в виде гарантированных (минимальных) или средних (медианных) значений. При этом предполагается, что распределение указанных величин подчиняется нормальному или логнормальному закону. Учитывая тот факт, что критерии предельных состояний (предел текучести, временное сопротивление, относительное удлинение и др.) являются положительными величинами, примем распределение R логнормальным: R ~ LN(m_R,vR²~). Функция логнормального распределение имеет вид (для v < 0,3):

P(R < г) = LN(mR,vR) = r

• 1   {    ( (lnx — m_R)²

= 42^VR\ ^exp\     2VR

При этом справедливо выражение:

R_P = Mr^ exp(u(P) • Vr),        (4)

где    RP- значение характеристики соответ ствующей вероятности превышения P;

M_r - медиана,

M_r = ex'p(m_R);

\ dx k (3)

v_R - коэффициент вариации;

u(P) - квантиль нормального распределения, соответствующий вероятности P, и определяемый из уравнения (5)

1     U⁽P)    _t2

P = ^=\ e~dt       (5)

у 2П -го

Если известны гарантированные значения, как правило, соответствующие обеспеченности 5%, то при заданном значении v_R можно определить параметр логнормального распределения m_R на основе выражения (6):

mR = —u⁽0.05) • Vr + ln(R₀._0S),     (6)

Таким образом, критерии предельного состояния полностью определены и для оценки вероятности разрушения остается определить параметры Q.

Построение плотности распределения нагрузки

Величина Q может быть оценена на основе натурного эксперимента или численного расчета. В обоих случаях указанная величина является случайной величиной, поскольку, зависит от изменчивости параметров геометрии (допуски, указанные в конструкторской документации), механических характеристик, погрешности расчетной модели и расчета, параметров кривой нагружения. При этом поскольку значение Q является результатом влияния относительно большого числа входных параметров - в первом приближении на основе предельной центральной теоремы теории вероятности можно принять распределение Q также нормальным или логнормальным. Поскольку отличие нормального закона от логнормального в случае v < 0,3 и в области практического применения в данной задаче не существенно, то принимается, что Q имеет логнормальное распределение. Соответственно, плотность распределения pQ определена. Тогда справедливо равенство: P(R < Q) = P(R/Q < 1), или, что тоже самое

1   [^в     t²

P(R2dt,   (7)

\2п -го где предел интегрирования 0 определяется по формуле 8:

0 =

ln(MQ/MR)

]^vQ + ^vR

Таким образом, для построения кривых вероятности отказа необходимо определить математическое ожидание Mq и коэффициент вариации Vq для каждого уровня нагрузки N, т.е. Mq = Mq(N),Vq = v q(N).

Для построения кривой вероятности отказа в качестве медианной нагрузки N₀,5, приводящей к разрушению с вероятностью 0,5, нужно решить уравнение М q(N₀,₅~) = M_r . При нелинейном многопараметрическом нагружении зависи-

M[Q(N,xk)] = M

[qNMxJ

+

dQ ^дХк^_х. ^хк

(^xk

мость Mq = Mq (N) также нелинейная, стоит отметить, что математическое ожидание зависит от функциональной зависимости, и в общем случае M[z(a,b,..,x)] Ф z(Ma,Mb,^,Mx), где а, Ь, х - переменные, Ma, Mb, Мх - соответствующие математические ожидания случая нагружения.

В случае сложной функциональной зависимости нагрузки от параметров нагружения учет влияния изменчивости входных данных на окончательной результат может быть выполнен на основе разложения в ряд Тейлора

^Х дх_кдх_т\_м^ (^Хк - ^МХк)^(хт - ^Мх_т) +

^-MxJ + 1/2

.XQ^xJ+ixdQi ^ ,

^Mxk

где xk - входной параметр расчетной модели (геометрические размеры, механические и физические свойства и т.п.);

S ² °Хк

- дисперсия параметра Хк.

Мх„ хк метра xk;

– математическое

ожидание пара-

Аппроксимация второй производной по параметру дается выражением:

^q\ d2

^Хкх=м.

<4/

Q(Mx_k+ SMxJ - 2 x Q(Mxk) + Q(Mxk - 8Mx9

^xk

(6Mxky

,

где   8М - приращение аргумента, определяется по выражению:

8Mx_k = u(0,95) x Sx_k.

Таким образом, Mq(N) и SQ (N) определяются выражениями:

M[Q(N,xk)] = Q(N,Mx_k) + ^ k

Q(N,Mx_k+ SMxJ - 2 x Q(N,Mx_k) + Q(N,Mx_k

sQ^(N,Mx_k) = lx^

^{2 x u}2,95

(Q(N,Mxk + SMxk) — Q(N,Mxk - SMxktf

- SM_x9 ^xk

,

k

Кривая вероятности отказа в зависимости от нагрузки N будет иметь вид:

^u295

.

1    в(Ю _t2

P(R

\2п -ж

где 0 (N) - предел интегрирования, определяется по формуле

кривых вероятности отказа с различным уровнем обеспеченности W.

Относительная погрешность программы

ANSYS - 15 % (v_U = 0,09).В этом случае случайная величина Q представляется выражением:

^Q= ^MQ ^eQ ^eU,

0(N) =

Iu(Mq(N)/Mr)

где

^vQ⁽N) + vR

.

eQ, e_U — логарифмически нормально рас-

Коэффициент вариации определяется зависимостью

_ Sq(N)

Vq( )  Mq(N)

В случае применения для анализа напряженно-деформированного состояния (НДС) численных пакетов САЕ – программ (например, ANSYS) выражение (15) необходимо скорректировать путем учета указанной в аттестационном паспорте неопределённости, вносимой самой программой (эпистемическая неопределенность). Она может быть учтена в рамках определения

пределенные величины с единичной медианой и логарифмически стандартным отклонением Vq, v_u, соответственно. При этом вероятность отказа будет определена соответствующих уровней обеспеченности W:

0_W(N =

Iu(Mq(N)/Mr)

Jv-⁽N) + vR

+ u(W)v_U.  (18)

Применение разработанного подхода представлено ниже на примере проектирования узла обтюрации ГИС представленного на рисунке 2.

В целом, реализация представленного выше подхода состоит из четырёх основных эта-

пов, каждый из которых делится на подэтапы (Рисунок 3).

Этап 1. Выбор критериев отказа узла обтюрации

Важным моментом Этапа 1 является выбор критерия нарушения работоспособности (критерия отказа). В соответствии с [4] наиболее мерных материалов при концентрации напряжений является раздир и прокол.

В силу того, что уплотнительная подушка узла обтюрации функционирует в условиях сложного нагружения и концентрации напряжений, то в качестве критерия отказа было принято разрушение подушки в результате её прокола острыми кромками металлических колец при превышении известными видами разрушения упругих поли- допустимого усилия в месте контакта.

Рисунок 2 – Узел обтюрации цилиндрической формы: а) –узел в сборе; б) – уплотнительная подушка в разрезе (размеры в мм)

Рисунок 3 – Основные этапы методологического подхода оценки надежности узла обтюрации

Величина допустимого внедрения кромок колец может быть определена по приближённой эмпирической зависимости нагрузки при проколе от модуля упругости и радиуса скругления индентора [3]:

Tkput^I^-R^^-H, (19) где E1 - модуль упругости с учётом перераспределения напряжений, за счёт коэффициента концентрации. E1 = 0,1ппр, где σпр – условный предел прочности материала;

R₀ - радиус скругления кромки кольца.

Условие работоспособности узла обтюрации может быть представлено в виде:

Т< Г_Кр_ИТ,              (20)

где   Т - максимальное усилие в месте прокола подушки, определяемое по результатам численного моделирования.

Этап 2 Конечно-элементное моделирование функционирования узла обтюрации

На этапе 2 построена расчётная конечно элементная модель и определены нагрузки и граничные условия (Рисунок 4).

Так как основной целью расчёта является демонстрация методологического подхода, то конструкции узла обтюрации и ГИС представлены упрощенно

Метрические ^^ перемещений

Рисунок 4 - Расчётная конечноэлементная модель

Анализ выполнен с помощью программного комплекса Ansys Mechanical 2022R1 с использованием решателя Autodyn в явных Лагранжевых координатах. С целью снижения затрачиваемых ресурсов ЭВМ задача решалась в осесимметричной постановке.

Давления в расширительной камере принято монотонно возрастающим.

В части задания свойств материалов главный интерес представляет модель материала уплотнительной подушки. Поведение гиперупругих материалов может быть описано с помощью известных моделей – Муни-Ривлина, Нео-Гука, Огдена и др. В данном случае, для выполнения расчётов, была принята 3-х параметрическая модель Муни-Ривлина, как обеспечивающая минимальные отклонения друг от друга расчетных и экспериментальных значений компонентов НДС [1].

При построении кривой вероятности отказа в качестве неопределенностей были приняты механические свойства материала уплотнительной подушки (зависимость напряжений деформаций – кривая «Нагружение – разгрузка»), диаметр камеры - D_KaM, диаметр подушки - D и толщина подушки - Н. Размеры металлических колец приняты постоянными.

На основании зависимостей 4 и 6 были определены значения варьируемых параметров. Каждой комбинации присвоен номер, соответ- ствующий номеру расчёта напряжённо-деформированного состояния с учётом вариации механических свойств и геометрических параметров. Комбинации варьируемых параметров – средних и с обеспеченностью 5% и 95 % приведены на рисунке 6. Для зависимостей напряжений от деформаций в столбце «Значение» знаком плюс отмечены параметры с 5 % обеспеченностью, знаком минус – параметры с 95 % обеспеченностью. Мед. – медианное значение.

Таблица 1 – Комбинации варьируемых параметров (продолжение таблицы не показано)

В результате проведения расчётов были получены картины напряжённо-деформированного состояния подушки для каждой комбинации варьируемых параметров на всех стадиях нагружения.

На рисунке 5 представлена общая картина НДС. Красным, оранжевым и желтым отмечены наиболее нагруженные области в результате взаимодействия с острыми кромками металлических колец.

Рисунок 5 - Общая картина НДС (косой разрез на кольцах и малое металлическое кольцо не рассмотрены)

Полученные картины НДС подтверждаются результатами натурных испытаний. На рисунке 6 видны следы разрушения подушки в виде прокола в результате внедрения острых кромок металлических колец.

а)

Рисунок 6 – Следы разрушения (прокола) подушки острыми кромками: а) – Подушка обтюраторная с металлическими кольцами;

б) – подушка обтюраторная отдельно

б)

В таблице 2 приведен фрагмент результатов расчётов усилия прокола в зависимости от давления, полученный для 35 комбинаций варьируемых параметров.

Этап 3 Построение кривых вероятности отказа от давления

По данным, приведенным в таблице на рисунке 9, с помощью зависимости 12 построена результирующая кривая математических ожиданий усилия прокола от давления (Рисунок 7).

Таблица 2 – Результаты расчётов усилия прокола в зависимости от давления газов (продолжение таблицы не показано)

На рисунке 8 приведены зависимости вероятности отказа по критерию прокола от давления, построенные на основании выражения 14, с уровнем обеспеченности 5 %, 50 % и 95 %. Пределы интегрирования для соответствующих уровней обеспеченности определены с учётом выражений 14 и 16.

Давление, МПа

Рисунок 7 – Результирующая зависимость математического ожидания усилия прокола от давления газов

При определении пределов интегрирования, в соответствии с уравнением для критерия отказа, на основании зависимости 14, принято значение максимально допустимого усилия прокола M_R. Для коэффициента вариации критерия прочности принято значение v_R=0,05.

1,2

5%       50%       95%

Рисунок 8 – Зависимость вероятности отказа (разрушения) уплотнительной подушки от давления ПГ (с учётом погрешности расчёта программного пакета Ansys)

Этап 4 Определение надежности узла обтюрации

Для определения надежности проектируемого узла обтюрации, полученные кривые вероятности отказа необходимо сравнить с кривыми вероятностями отказа референтного узла обтюрации.

В случае отсутствия референтных узлов обтюрации надежность может быть оценена консервативно в соответствии с известными данными по вероятности возникновения аварий типового оборудования, наиболее близкого по назначению.

Например, если принять ГИС как сосуд под давлением, то в соответствии с [6] вероятность разрушения может быть принята 2,7·10^-8 (Таблица 3).

Таблица 3 - Обобщенные данные по вероятностям инициирования аварий типового технологического оборудования

Заключение

Разработан статистический подход к проектированию узла обтюрации ГИС, учитывающий неопределенности, обусловленные разбросами свойств материалов его элементов, отклонениями размеров, стохастичностью нагрузок и погрешностями программно-математического аппарата.

Статистический подход основан на оценке надежности функционирования узла обтюрации ГИС. За основной критерией надежности узлов обтюрации принимается их способность герметизировать камеру от прорыва ПГ с вероятностью не менее заданной.

Подход основан на строгом математическом обосновании, что позволяет давать консервативную оценку надежности узла обтюрации при минимальном количестве расчётов.

Построены кривые вероятности отказа узла обтюрации в зависимости от давления ПГ и проведена его оценка с учетом неопределенности различного рода, вносимых элементами узла обтюрации и процессами, происходящими при функционировании ГИС.

Учёт неопределенностей позволяет снизить трудоёмкость разработки узла обтюрации ГИС, а также снизить риски отказа как разрабатываемого узла, так и всей газодинамической импульсной системы.