Конструирование эффективных фронтов инновационных проектов

Определение приоритетности финансирования инновационных проектов основано на системном анализе их эффективности. Этот анализ предполагает расчёт и анализ ряда локальных показателей эффективности, каждый из которых характеризует различные аспекты в процессе реализации проекта. Зачастую эти частные показатели являются противоречивыми, а динамика их поведения может носить несистемный и/или антагонистический характер. В этих случаях требуется разработка процедур, обеспечивающих свёртку частных оценок эффективности в обобщённый интегральный показатель. Конструктивным способом такой свёртки является метод Data Envelopment Analysis (далее по тексту статьи – DEA) [1], позволяющий реализовать агрегирование частных оценок в единую обобщённую, на основе которой возможно однозначное сопоставление и ранжировка объектов оценивания – инновационных проектов.

Как правило, при реализации метода DEA некоторое множество объектов оценивания получают одинаковые максимальные оценки, что однозначно определяет их наивысший приоритет в анализируемой совокупности и свидетельствует об их равнозначности.

В этом случае актуальной является задача исследования такой равнозначной совокупности объектов, имеющих максимальный приоритет. Для её решения возможно построение фронтов эффективности, которые определяют границы зон максимальной эффективности и наглядно иллюстрируют положение проектов с максимальной эффективностью относительно анализируемой совокупности в пространстве состояний.

Конструирование эффективных фронтов предполагает решение следующих задач.

• 1)    математическая формализация DEA-моделей на основе системы локальных показателей эффективности инновационных проектов - определение вида обобщённого показателя эффективности и системы ограничений.

• 2)    сбор и систематизация исходных данных о значениях локальных характеристик эффективности инновационных проектов.

• 3)    численная реализация алгоритма DEA-оценки - расчёт значений обобщённого показателя сравнительной эффективности на основе решения задач математического программирования.

• 4)    ранжирование совокупности анализируемых инновационных проектов на основе полученных системных оценок эффективности.

• 5)    конструирование эффективных фронтов инновационных проектов в пространстве параметров функционирования.

Рассмотрим пример проведения многокритериальной оценки эффективности инновационных проектов и построения эффективных фронтов в трёхмерном пространстве.

1 Метод исследования

Особенностью метода DEA является использование формальных алгоритмов оценивания без учёта субъективных суждений исследователя о значимости (весе) локальных характеристик [2].

Свойства метода и алгоритм применения рассмотрены в работе [3], результаты апробации для решения различных задач оценки сравнительной эффективности представлены в материалах [4].

Для применения метода DEA объекты оценивания представляются в виде систем, которые характеризуются m входными - X_m и к выходными - Y k параметрами. При этом увеличение выходных характеристик и уменьшение входных должно приводить к росту обобщённого показателя эффективности, и наоборот.

Как правило, в качестве выходных параметров Y k выбираются характеристики системы, определяющие результаты функционирования: выпуск продукции и услуг, создание технологий и т.п.

В качестве входных характеристик X_m выступают затраты различных ресурсов, которые определили наличие этих результатов.

В базовом варианте метода DEA обобщённый показатель эффективности исследуемых систем формируется как отношение взвешенных аддитивных наборов выходных характеристик к входным:

f ₌ u i • Y i + u 2 • ^Y2 + ... + u k • ^Y_k v 1 • X 1 + v 2 • X 2 + ... + ^Vm ' X m

.

В обобщённом показателе эффективности (1) u i ( i = 1, 2,..., k ) - положительные, произвольные и заранее неизвестные весовые коэффициенты, определяющие значимость каждого выходного фактора Y i в системном показателе эффективности f. Соответственно, V j (j' = 1,2,..., m ) - веса входных величин X j .

Процедура нахождения численных значений обобщённых показателей интегральной оценки эффективности f для каждой системы предполагает их ранжировку на единичном интервале. Такая ранжировка обеспечивается максимизацией обобщённого показателя (1) для каждой оцениваемой системы с помощью нахождения набора весовых коэффициентов ui, vj на основе решения задачи математического программирования при системе ограничений, определяющей область значения этих весов:

• U11 • Уп + u21 • Y21 + u31 • Y31 + ... + uk 1 • Y 1

V _n • X _n + v 21 • X 21 + v 31 • X 31 + ... + v m 1 • X m 1

• U12 • Y12 + u22 • Y22 + u32 • Y32 + — + Uk2 " Yk2

• ^v 12 • X 12 ⁺ v 22 • X 22 ⁺ v 32 • X 32 ⁺ ... ⁺ v m 2 ' X m 2

• U1 n ' Y1 n + u2n ‘ Y2n + u3n " Y3n + ... + ukn ‘ Ykn   <

• ^v 1 n ^- X 1 n ⁺ v 2 n ' X 2 n ⁺ v 3 n ' X 3 n ⁺ ... ⁺ v mn ' X mn

  
  

_ u n >  0 ; V jn >  0 ;

i = { 1 , 2 ... k } ; j = { 1 , 2 ... m } ; n = { 1 , 2 ... N } .

Отметим, что применение этого метода возможно как в пространствах параметров и характеристик сравниваемых систем, так и на временных интервалах функционирования одной системы. В этом случае метод DEA позволяет проводить анализ динамики обобщенного показателя сравнительной эффективности исследуемой системы.

Наряду с использованием обобщенного показателя эффективности в виде отношения (1) применяются линейные конструкции - аддитивные наборы факторов, требующих максимизации для обеспечения роста значений системной эффективности.

2    Объект исследования и исходные данные

Объектом исследования является совокупность инновационных проектов, агрегированная технопарком «Жигулёвская долина» [5].

В качестве локальных характеристик инновационных проектов будем использовать следующие общепринятые частные показатели:

• ■    PV - стоимость проекта, руб.;

• ■    E - объём товарного рынка, руб.;

• ■    CP - рентабельность проекта, %;

• ■    IC - требуемые инвестиции для реализации проекта, руб.

Эти показатели получили широкое распространение при формировании заявок на отбор и финансирование инновационных проектов. Они позволяют сопоставлять различные проекты и определять их эффективность.

Однако, даже минимизируя состав локальных параметров оценки, сделать однозначный выбор при наличии множества альтернативных проектов затруднительно, так как проекты могут иметь различный масштаб, первоначальную стоимость, потенциальный размер товарного рынка, запрашиваемый объём финансирования, а также сроки окупаемости и реализации.

Для решения задачи оценки и выбора проектов необходимо использовать процедуру, обеспечивающую свёртку локальных характеристик в единый обобщённый системный показатель эффективности, например метод DEA.

3    Многокритериальное сравнительное оценивание эффективности инновационных проектов

На первом этапе реализации DEA-метода необходимо определить вид обобщённого показателя оценивания. При формировании этого показателя используется принцип аддитивной свёртки трёх относительных локальных характеристик: удельной стоимости проекта, объёма товарного рынка по отношению к требуемым инвестициям и рентабельности проекта. В этом случае обобщённый показатель имеет следующий вид:

• ^v 1 +

E 1 ic J

• v 2 + CP • v 3 ^ max,

где:

• ■    PV, IC, E, CP - соответствующие локальные характеристики проекта;

• ■   v 1 - v₃ - весовые коэффициенты, определяющие вклад локального показателя в обобщён

ный критерий.

Конструирование обобщённого показателя на основе только относительных характеристик позволяет учитывать фактор масштаба и адекватно сравнивать проекты, имеющие различные объёмные параметры – первоначальную стоимость, требуемые инвестиции, объём целевого рынка.

Следующим этапом реализации DEA-метода является сбор исходной информации относительно выбранных локальных характеристик для конкретного набора инновационных проектов.

На основе собранной информации о 22 инновационных проектов, заявленных к реализации в Самарской области, формируются их DEA-модели для обобщённого показателя вида (3).

Система (4) определяет DEA-модель первого проекта по обобщённому показателю (3) с соответствующей системой ограничений.

DEA-модели вида (4) для остальных проектов различаются численными значениями переменных в обобщённых показателях, которые берутся на основе значений локальных характеристик для каждого инновационного проекта. Система ограничений остаётся постоянной.

Таким образом, для нахождения значений оценок системной эффективности для каждого проекта необходимо сформировать 22 постановки задачи линейного программирования вида (4) и найти их решения.

Результаты решения этих задач показаны на графике, представленном на рисунке 1 (по горизонтальной оси показаны условные номера инновационных проектов).

Анализ полученных результатов показывает, что максимальную системную оценку эффективности f = 1,0000 имеют три проекта: №1, №4 и №5. Минимальное значение имеет проект №10 – f = 0,0068. Высокое значение системной эффективности имеет и проект №18: f = 0,9554 (см. рисунок 1).

Диаграмма на рисунке 2 показывает ранжирование проектов по убыванию показателя системной эффективности (по горизонтальной шкале отложены порядковые номера проектов). Ранжировка позволяет выделит следующие группы приоритетов.

• ■    Четыре проекта - №№ 1, 4, 5, 18 - можно отнести к группе наивысшего приоритета.

• ■    Вторая по приоритетности группа проектов включает шесть проектов со значениями f от 0,1954 до 0,076 – это проекты №№ 8, 13, 3, 7, 22 и 19.

• ■    Двенадцать проектов имеют оценку системной эффективности менее 0,05. К этой группе, имеющей низкий приоритет, относятся проекты №№ 20, 6, 16, 15, 14, 17, 21, 2, 11, 9, 12 и 10.

, ( 1510200 )     ( 14900000000 )

f =           - v +                - v₉ + 22 - v^ ^ max;

₁     1 1      1      23

' ( 1510200 / 1 ) - v 1 + ( 14900000000 / 1 ) - v ₂ + 22 - v 3 <  1 ;

( 20874000 / 20874000 ) - v 1 + ( 124000000000 / 20874000 ) - v ₂ + 20 • v 3 <  1 ; ( 12500000 / 12000000 ) - v 1 + ( 32500000000 / 12000000 ) - v ₂ + 132 . 5 - v 3 <  1 ; ( 100000000 / 1 ) - v 1 + ( 50000000 / 1 ) - v ₂ + 15 - v ₃ <  1 ;

( 204030000 / 153052000 ) - v 1 + ( 5200000000 / 153052000 ) - v ₂ + 1024 - v ₃ <  1 ; ( 103000000 / 43000000 ) - v 1 + ( 17200000000 / 43000000 ) - v ₂ + 35 - v ₃ <  1 ; ( 10965000 / 4500000 ) - v 1 + ( 60300000000 / 4500000 ) - v ₂ + 100 . 3 - v ₃ <  1 ; ( 1365000 / 1300000 ) - v 1 + ( 634000000000 / 1300000 ) - v ₂ + 200 - v ₃ <  1 ; ( 1759985300 / 1758885300 ) - v 1 + ( 10000000000 / 1758885300 ) - v ₂ + 11 - v ₃ <  1 ; ( 37125000 / 3000000 ) - v 1 + ( 14300000000 / 3000000 ) - v ₂ + 7 - v ₃ <  1 ;

( 1400000000 / 400000000 ) - v 1 + ( 100000000 / 400000000 ) - v ₂ + 20 - v ₃ <  1 ;

• < ( 655200000 / 12000000 ) - v 1 + ( 10000000000 / 12000000 ) - v ₂ + 11 - v ₃ <  1 ; ( 191132600 / 60000000 ) - v 1 + ( 1000000000 / 60000000 ) - v ₂ + 133 - v ₃ <  1 ; ( 22000000 / 10000000 ) - v 1 + ( 1000000000 / 10000000 ) - v ₂ + 23 - v ₃ <  1 ; ( 45000000 / 18500000 ) - v 1 + ( 5000000000 / 18500000 ) - v ₂ + 25 - v ₃ <  1 ; ( 244860000 / 27860000 ) - v 1 + ( 50000000000 / 27860000 ) - v ₂ + 30 - v ₃ <  1 ; ( 100000000 / 50000000 ) - v 1 + ( 2000000 / 50000000 ) - v ₂ + 23 - v ₃ <  1 ; ( 94463000 / 1 ) - v 1 + ( 50000000 / 1 ) - v ₂ + 25 - v ₃ <  1 ;

  
  

  ( 16096000 / 2500000 ) - v 1 + ( 70000000 / 2500000 ) - v ₂ + 77 . 8 - v ₃ <  1 ; ( 15000000 / 10000000 ) - v 1 + ( 70000000 / 10000000 ) - v ₂ + 40 - v ₃ <  1 ; ( 26212000 / 15000000 ) - v 1 + ( 40000000 / 15000000 ) - v ₂ + 22 - v ₃ <  1 ; ( 113600000 / 120000000 ) - v 1 + ( 240000000 / 120000000 ) - v ₂ + 100 - v ₃ <  1 ;

v 1 , v ₂ , v ₃ >  0 .

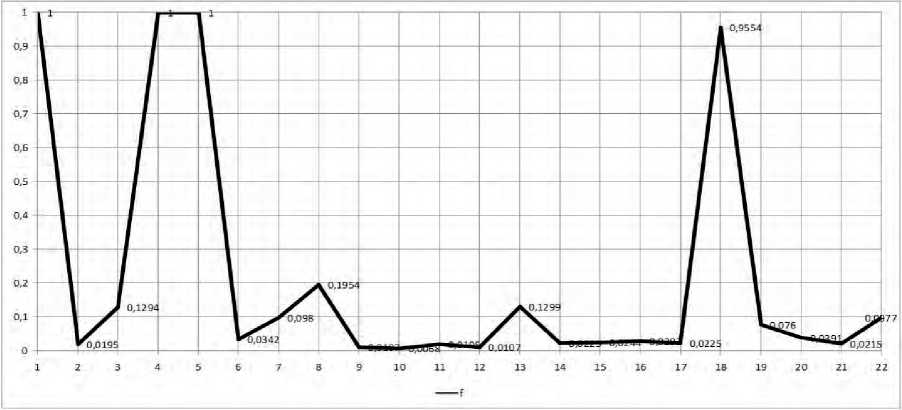
Рисунок 1 – Значения системной эффективности проектов по обобщённому показателю f

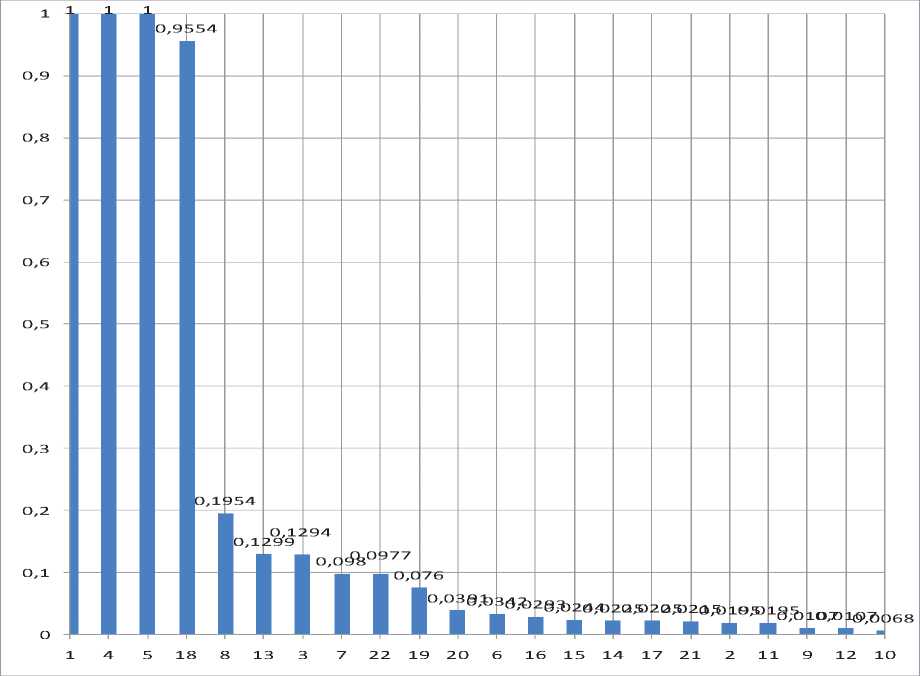
Рисунок 2 – Ранжированные значения системной эффективности проектов по обобщённому показателю f

4 Конструирование эффективных фронтов инновационных проектов

Для трёх проектов с максимальной оценкой системной эффективности построим эффективные фронты. Эти фронты определяют секторы, в пределах которых возможны изменения весовых коэффициентов в обобщённом показателе эффективности без уменьшения максимальной системной оценки эффективности проекта.

В случае обобщённого функционала (3) фронты можно наглядно отобразить в трёхмерном пространстве весовых коэффициентов v 1 , v 2 , v 3 .

В общем виде фронты формируются объединением плоскостей, заданных уравнениями вида:

+

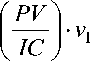
E 1

IC J

• v 2 + CP • v 3 = 1 ,

где v 1 , v 2 , v 3 – численные значения весов, определяемые из решения задач линейного программирования вида (4) для трёх эффективных проектов №№: 1, 4, 5.

Для проекта №1 эффективный фронт формируется плоскостью, заданной уравнением:

• (6)                1510200 • v 1 + 14900000000 • v ₂ + 22 • v ₃ = 1 .

Для проекта №4 эффективный фронт формируется плоскостью, заданной уравнением:

• (7)                100000000 • v 1 + 50000000 • v ₂ + 15 • v ₃ = 1 .

Для проекта №5 эффективный фронт формируется плоскостью, заданной уравнением:

1 , 33 • v 1 + 33 , 98 • v ₂ + 1024 • v ₃ = 1 .

В таблице 1 представлены значения координат точек пересечения плоскостей, формирующих эффективные фронты, с осями координат в пространстве весов.

Таблица 1 – Значения координат точек пересечения плоскостей с осями координат

Порядковый номер проекта	Плоскость	Значения весов (координаты точек)
		v 1	v 2	v 3
1	A	6.62×10-07	6.71×10-11	4.55×10-02
4	B	1.00×10 -08	2.00×10 -08	6.67×10-02
5	C	7.50×10-01	2.94×10 -02	9.77×10-04

На рисунке 3 в трёхмерной системе координат показаны плоскости, формирующие эффективные фронты, и эффективная граница. Так как различия между значениями координат точек составляют порядки, то в системе координат на рисунке 3 для наглядности масштаб не учитывается.

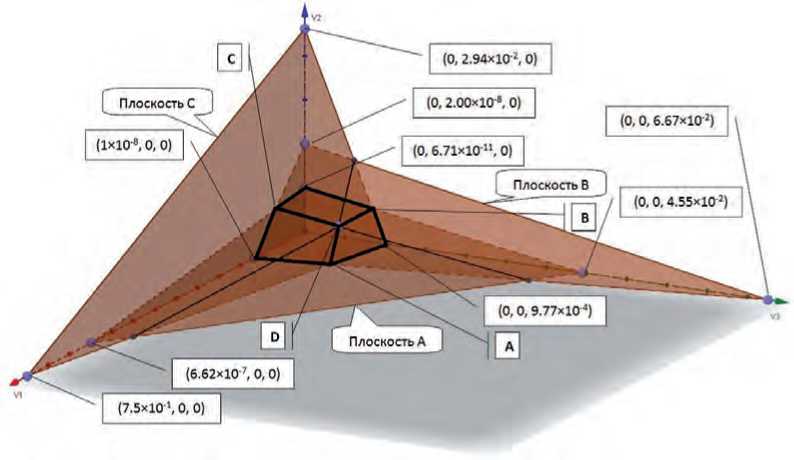
Рисунок 3 – Эффективные фронты в пространстве весов локальных характеристик инновационных проектов (координаты точек показаны условно, без учёта масштаба)

Как видно из построений, показанных на рисунке 3, эффективные фронты формируют многогранник (выделен жирными линями), состоящий из трёх пересекающихся плоскостей. Границы многогранника определяются тремя точками пересечения с осями координат и четырьмя характерными точками (A, B, C, D) взаимного пересечения плоскостей. Каждая плоскость определяет области максимальной эффективности для соответствующих проектов.

Координаты характерных точек представлены в таблице 2.

Таблица 2 – Координаты характерных точек

Характерные точки	Значения весов (координаты точек)
	v 1	v 2	v 3
A	9.854×10-9	0	9.766×10-4
B	0	6.567×10-11	9.766×10-4
C	9.967×10-9	6.61×10-11	0
D	9.821×10-9	6.468×10-11	6.468×10-11

Эффективный фронт определяет континуум значений локальных оценок эффективности, в пределах которого возможны их изменения при сохранении максимальной оценки эффективности проекта.

Все остальные, неэффективные проекты находятся вне этого фронта. Под термином «неэффективный проект» будем понимать проект с оценкой системной эффективности, отличной от единицы.

Площади соответствующих граней эффективного фронта можно трактовать как меру устойчивости проекта к изменению локальных показателей качества в условиях неухудше-ния его системной эффективности.

Для остальных 19 анализируемых проектов плоскости эффективных фронтов определяют направления изменения частных характеристик для достижения эталонной группы, состоящей из трёх проектов с максимальными оценками системной эффективности.

Исходя из этой гипотезы можно сделать вывод, что подобное фронтирование позволяет указать направления изменения локальных характеристик инновационных проектов для достижения проектом максимальной эффективности.

Основываясь на этом выводе, может быть разработан алгоритм управления локальными характеристиками неэффективных проектов, позволяющий максимизировать их оценку системной эффективности – выводить эти проекты на границы фронтов.

Заключение

В проведённом исследовании реализована процедура многокритериального оценивания сравнительной эффективности инновационных проектов на основе DEA-модели, предложена постановка обобщённого показателя системной эффективности проектов, построена система ограничений.

Постановки DEA-моделей формализованы в форме задач линейного математического программирования. Решения этих задач определяют численные значения обобщённого показателя эффективности для каждого из рассмотренных проектов.

Построены эффективные границы – фронты в трёхмерном пространстве параметров, определены допустимые (эффективные) секторы изменения локальных характеристик проектов, имеющих максимальную оценку эффективности. Дана содержательная интерпретация секторов эффективного фронта в пространстве весовых коэффициентов обобщённого показателя системной эффективности.

Исследование выполнено при финансовой поддержке РФФИ, проект: «Системное ранжирование инновационных проектов экосистемы Самарской области» (грант № 15-4602135).