Конструирование точных решений в космологии, основанной на гравитации Хорндески

The inflationary paradigm implying the accelerated expansion of the early universe is often considered as a. successful explanation for the origin of it’s structure. The first models of cosmological inflation were built on the basis of General Relativity (GR) in 4D Friedmann-Robertson-Walker (FRW) space-time under the assumption of the existence of some scalar field (inflaton) which is the source of the accelerated expansion of the universe [1-4].

Also, for a. more correct understanding of the nature of processes at the stage of inflation, the exact solutions of cosmological dynamic equations were considered (see, for example, [5]). The exact cosmological solutions were obtained for a. large number of inflationary models based on GR. The classification of the methods for generating them (and the exact solutions themselves) for inflation in frame of Einstein gravity can be found, for example, in [5,6].

Nevertheless, after the discovery of the repeated accelerated expansion of the universe at the present time, cosmological models with various modifications of Einstein gravity were proposed for

• ¹    E-mail: ingvor@inbox.ru

its explanation or, in other words, to explain the nature of dark energy which include, among others, scalar-tensor gravity theories and Einstein-Gauss-Bonnet gravity [7-9].

Scalar-tensor gravity with non-minimal coupling of a scalar field with curvature are important extensions of GR which can explain the initial inflationary evolution, as well as the late accelerating expansion of the universe [10,11]. The examples of inflationary models on the basis of scalar-tensor gravity (STG) theories with the exact solutions can be found in [10-12] and in many other works as well. Furthermore, the transformations of the dynamical equations from models based on STG to ones in frame of GR are presented in [13].

For the very early universe approaching the Planck scale one can consider Einstein gravity with some corrections as the effective theory of the quantum gravity. The effective supergravity action from superstrings induces correction terms of higher order in the curvature, which may play a. significant role in the early Universe. The one of such correction is the Gauss-Bonnet (GB) term in the low-energy effective action of the heterotic strings [14]. Also, the GB term arises in the second order of the Lovelock gravity which is the generalization of the Einstein gravity [15].

The exact solutions for cosmological models on the basis of Einstein-Gauss-Bonnet gravity with nonminimal coupling of a. scalar field with GB-scalar in 4D Friedmann universe were considered in [13,16-18]. The connection of such cosmological models with the standard inflation based on GR one can find in [13,17,18], also.

The method for constructing the exact solutions for cosmological models in Friedmann universe that contain GR, STG and EGB as the special cases of the Horndeski gravity is proposed in this paper. Such a connection is parametrized by means of constant parameters « g_B and (3g_T whose choice will determine the type of gravity on the exact solutions of the cosmological dynamic equations.

1.    Inflation with the Horndeski gravity in Friedmann universe

The most general single-field Lagrangian giving rise to second-order dynamical equations was proposed by Horndeski [19] on the basis of the action

S — ^ d4x^—g(L2 + L3 + L4 + L5)(1)

with the following Lagrangians

L2 — К (ф,X), L3 — —Gз(ф,X)Пф,(2)

L4 — G4 (ф,X)R + G4,x [(Пф)2 - (V^V,ф)(V^V"ф)] ,(3)

L5 — G 5 (ф, X)G^V ^ Vф - ¹ G 5 ,x [(Пф)³ - 3(□ф)(V_дV,ф)(V^V"ф) +

2(VцVaф)(V“V 3 ф)(V^Vмф)],(4)

where X — —V_мфV^мф/2, Пф — V_MV^; also, К, G₃, G 4, G 5 are the some functions of ф and X; G j,_x (Ф,X ) — dQ j (ф,X )/dX with 3 — 4,5 [20,21].

Thus, the different types of gravity can be defined from the action (1) for different functions К, G3, G4, G5. For generating the exact cosmological solutions with Horndeski gravity one can find the constants of motion from the Noether symmetry [22] that gives some exactly solvable classes of models for certain functions К, G3, G4, G5.

Nevertheless, it is possible to consider the generalized exact cosmological solutions on the basis of some types of well known gravity theories which are unified by the Horndeski gravity. The generalization of the exact solutions lies in the fact that they are suitable for cosmological models with General Relativity, scalar-tensor gravity and Einstein-Gauss-Bonnet gravity as well.

We will investigate the models on the basis of the following choice of the functions К, G3, G4, G5

for the Horndeski gravity [21,23,24]

К (ф, X) = wX - V(ф) - Ц"" Х2 (3 - ln X),(5)

G3 (ф,Х) = -2^'Х (7 - 3ln X),(6)

G4 (ф,Х) = 2F(ф) - 2^"Х (2 - lnX),(7)

G5 (ф,Х)=2£ф ln X,(8)

to unify some types of gravity theories, namely General Relativity (GR), scalar-tensor gravity (STG) and Einstein-Gauss-Bonnet (EGB) gravity.

The equations of cosmological dynamics at the stage of inflation in spatially flat 4D Friedmann universe in the system of units 8ttG = c = 1

ds² = -dt² + a²(t) ( dz² + dy² + dz² ,

similar to those obtained from the action

S =

I d⁴xV-g 2 F (ф)R

2 w^V ⁷ Э ц фЭ _и ф - V (ф) - 2 ^Rqb

(Ю)

where R2; _B = R pv_Pa R^ P¹⁷ - 4R ^_V R ^ ⁷ + R² is the Gauss-Bonnet scalar, can be written as [21,25]

Ei = 3FH2 + 3HF - ^ф2 - V(ф) - 12H3^ = 0,(11)

E2 = 3FH2 + 2HF + 2FH + F+ ^ф2 - V (ф) - 8H 3£ - 8HH £ - 4H 2< = 0,(12)

E3 = wф + 3wнф + |ф X + гф - 6H 2f; - 3Hf; + 12H 4^ф + 12H2 H Сф = 0.(13)

Moreover, for equations (11)—(13) one has the additional condition [25]

фE3 + Ei +3H(Ei -E2) = 0.(14)

Taking it into account we conclude that two equations from (11)—(13) are independent only.

Thus, one can obtain the following particular cases of cosmological models with the Horndeski gravity:

• •    F = 1, w = 1, £ = 0 - the case of General Relativity;

• •    F = F(ф), £ = 0, w = w(ф) - scalar-tensor gravity;

• •    F = 1, w = 1, £ = £(ф) - Einstein-Gauss-Bonnet gravity;

• •    F = F (ф), w = w(ф), £ = £(ф) - generalized scalar-tensor gravity, which includes the nonminimal coupling of a. scalar field with Ricci scalar and with Gauss-Bonnet scalar.

Now, we consider the possibility of the transformation of the equations (11)—(12) to the ones similar to cosmological dynamic equations for Einstein gravity

V _E (ф) =3H² + H, ф² = -2H.

Also, the equations (15)—(16) can be rewritten in terms of a. scalar field [26,27]

VE (ф) = 3H2 - 2Нф2, ф = -2h; , in frame of the Ivanov-Salopek-Bond method with the exact solutions based on the choice of H(ф).

To transform the equations (11)—(12) to the equations similar to (15)—(16) one can use the special choice of a functions F, w and £ which were considered earlier for scalar-tensor gravity and EinsteinGauss-Bonnet gravity separately [13]

^;'     (^) Ha 2 ,    ^{F (t)} =^{1 -} a^,   ^w(t) =^{1 - 3 sT} (Ha2),            ⁽¹⁹⁾

where “ g_B and ф s_T are coupling constants of a scalar field with Gauss-Bonnet and Ricci scalars.

After substitution (19) into equations E 1 + E 2 = 0 and E 1 — E 2 = 0 we obtain

V (ф) = 3H ² + H + 6a а _Св = V_E (Ф) + V_Gb (Ф)

Ф 2 = —2H, where VgB = 6a«gB is the additional term in the potential which arises due to the nonminimal coupling of a field with Gauss-Bonnet scalar. Also, the function F from (19) does not change the potential, i.e. VsTg = VB, moreover, one has the same Hubble parameter H and the scalar field ф for all considered types of gravity.

Furthermore, one can redefine the functions F, w and £ in terms of a scalar field on the basis of the expressions

As the result, we have

H = -2H’£, a = aH ,

а(ф) = a o exp

(—2 / H "ф)

,‘    “ gb a o / 1 f H Л

^Ф   4H2 H' exp I 2 J H' АФУ ф \ ф /

F (Ф) = 1 —

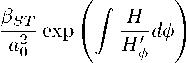
Цф)

³P st

⁺ 2a 0

( ^H )^exp (/ ^4

with corresponding potential and scalar field

V (Ф) = 3H ² — 2Hф² + 6a o “ GB H exp

(—2 / 4*)

Ф = —2Hф.

Thus, this approach generalizes two methods for generating the exact solutions of cosmological dynamic equations which are usually used for the case of GR, namely the method of fine tuning of the potential [5,28] and the Ivanov-Salopek-Bond method [5,26,27].

• 2.    The examples of generalized exact solutions

The solutions from GR power-law inflation

For power-law inflation with the Hubble parameter H = m/t we obtain the following exact solutions for the case of GR from equations (15)—(16)

ф(t) = V2m In t,

V _B (Ф) = m(3m — 1) exp

ф

and, respectively, from (19)—(21), we have the generalized solutions for power-law inflation based on the

*(t) = V2— In t, V(*) = —(3— - 1) exp -—* + 6«GBe0 — exp -—.   * [ V — J                [ y2— F(*) = 1 - ^ ^ 2 T exp ^-V2m*^ , w(*) = 1 + -—^2^T exp ^-V2m*^ , « gb d o       Г(— + 3) ^(*) = 0          exp    /^ * . 2—2(— + 3)    [ V2—

(31) ,                 (32) (33) (34) (35)

Horndeski gravity

with the functions К, G3, G4, G5 which can be obtained in explicit form by means of the expressions (5)-(8) using the solutions (31)-(35).

Thus, for « g_B = 0 and [3 g _T = 0 we have the exact solutions for inflation based on GR, for « g_B = 0 we have the exact solutions for inflation with STG and for P g_T = 0 we have the exact solutions for EGB inflation. As one can see, the background solutions for GR and STG are the same, however, the parameters of cosmological perturbations for inflationary models based on these gravity theories are different (see [21,25] for details).

The solutions from GR inflation with Higgs potential

Now, we consider the following Hubble parameter

H = nB exp(- At) + A,                               (36)

with corresponding scale factor

o.(t) = do exp

(At - ^

where A, B, A and n are arbitrary constants.

From equations (15)—(16) we have the exact solutions

*(t)=± V 8AB exp f- At).*

v (»)=3A2 *4+f3 4 - т) *2+3A2.

with Higgs potential [5,13].

From equations (19) we obtain

F (*) = 1 — ^ ^f ^exP ^f1 4

d0 \8nB у\4 /

„ fA* . 8 Г f^ .   ' exp f 1 *2).(41)

d0A2 у * у y8nB)у4 )

In the general case, we can not find the explicit dependence £ = £(t) from equation (19), but we can obtain it for the case of the choice of constants A, B and A.

For example, for A = 1, B = 1 and A = 1 we have

«*) = -'      ⁸ . (8 * 2) (i * 2 + 1) + _eEi f1,1 *2 + 1) - _3Ei f 1.1 *2)

2        ( 8 * 2 + 1) *2          V 8* У V 8* У

V gb (*) = 6а_Свпйо

(1+*2)exp (-8*2),

where Ei is the exponential integral function [29].

Thus, the potential for this model is

V(Ф) = V e (ф) + V Gb (Ф) = 3 + 3 Ф 4 + 5 Ф 2 + 6 « gb nao ( 1 + -8) exp —- 1 Ф²) .      (44)

64     8               ф    Ф Ф \ 8 /

In the case of a G_B = 0 we have the solutions for scalar-tensor gravity and general relativity with arbitrary constants A, В and A.

The solutions from GR inflation with generalized polynomial potential

Further, we consider the solutions on the base of the Hubble parameter

H (Ф) =     Ф”, n = 2,

thus, from equations (17)—(18) we obtain

^ф(t) =

"              a "1 2^-"

± ²ⁿ⁽ⁿ — ²⁾y - t

,

a(t) = ao exp

V e (Ф) = АФ2¹

±2

A It)"

,

2^ ф^^^ .

From the equations (24)-(27) we obtain P st    /Ф² A

^{F (Ф) = 1 —}     e^xp(2nj,

,Л. 3 P st .1    (Ф² A

Ш(Ф) = 1 + 2.200Ф exp(2n),

^^(ф) = ^a GB

V (Ф) = АФ2п

3V3 ao2

-1-

3 n

2 П

3 n 4

A3/2 (1 - 3 n)

2An2

Ф

3? exp (— 8П A W (

3n

’

3n 1 Ф² A "2"⁺ 2 ’ 4П ’

Ф2^{(( г} 1) + 2ao-n.V3A.a GB Ф" exp f— y-^ , у 4n у

where W (p,,v,z) is the Whittaker function [29].

For an explicit value of the constant n, for example, in the case when n = —2 we have

.....  (-, A ■)"

,

a(t) = a0 exp

(-^ A ■)

1/2"|

,

with

^{F (Ф)=1—} ^ St ^exp (^—4 ^Ф2)-^ш(Ф)=¹⁺1|Т ^Ф2^exp (^—4^Ф2),

^(Ф) =

3V3ao    ^6

A3A “^{GB Ф}

V (Ф) = Aф-4

8^-6 3 ^Ф

- 24Ф4 + 384Ф² - 3072) exp Q Ф2) , 4a o V3Aa GB Ф — 3 exp QФ²) .

For a G_B = 0 and P s_T = 0 we have Muslimov’s solutions for standard inflation [5,30]. The exact solutions for cosmological model with n = 2 one can find in [13].

The solutions from GR inflation with trigonometric potential

Further, we consider the exact solutions for the Horndeski gravity on the basis of ones in GR for the trigonometric potential which were firstly obtained in [26] and also were considered in [5].

For the Hubble parameter

H(ф) = A sin (Аф),

with A = (such a value of the parameter A was chosen in order to integrate the equation (24)) we have

ф(t) = V2arcsin

[tanh (V3A(t - t*))]

a(t) = a₀

[cosh (V3A(t - t*))]1/3 ,

V _E (ф) = -4A cos²

(^

+ 3A2.

From the equations (24)-(27) we obtain

F (ф) = 1 -

P st

a0 cos2

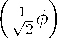
ш(ф)= 1+

³P st 2n² a0

tаnlG1lФ) cos2 (75 ф)

^ф) = —

« св а о

2A3 tan ( ^ф) ’

V (Ф) =

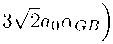
+ 3A2.

Thus, for the following value of the parameter « с_В =

( ²3a^ ^we have th^e model with flat potential

V = const which is induced by the non-mimimal coupling of the scalar field and Gauss-Bonnet scalar.

Conclusion

In this paper we considered the exact inflationary solutions for the Horndeski gravity which generalize solutions for several gravity theories. The transition between different models of gravity is carried out by selecting the constants « _св and P s _T- Using the proposed approach, one can generate the generalized exact solutions from the exact solutions obtained for the case of General Relativity.

Also, it is possible to obtain the other exact inflationary solutions for the Horndeski gravity from the initial case of Einstein gravity considering the conditions (19) or (24) for the integrability of models in the sense of finding the explicit dependence £ = £(ф).