Конструкционные средства обеспечения долговечности патрубков, трубопроводов с тонкостенными корпусными элементами

Хвесюк Олег Вячеславович, заведующий учебной лабораторией кафедры космического машиностроения учитывается также и действие внутреннего давления.

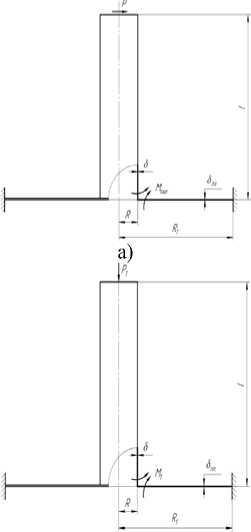
б)

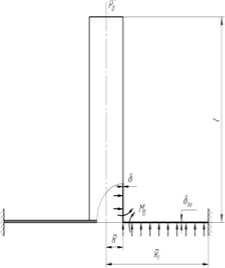
в)

Рис. 1. Случаи нагружения сочленения патрубка с корпусным элементом

При решении задачи о нагружении свободного торца патрубка поперечной нагрузкой, как это показано на рис. 1, использовались уравнения общей теории цилиндрических оболочек и уравнения асимметричного изгиба круглых пластин [1]. Разрешающее уравнение относительно потенциальной функции Φ(ξ,φ) приводится к виду:

д8ф д8ф д8ф д8ф    д8ф д6ф д6ф

If8 + 4 df6^^2 + 6 д^др* + 4 df2dp6 + др8 + 2u"df6 + 6 df4dp2 +

д6ф     д6ф 1 -и^д^ф            д4ф    д4ф

+2(4 -U) df2dp4 + 2др6 + с2 df4 +2(2 - Ц) df2dp2 + др4 = 0, где с2

б² 12R² '

Через функцию Φ(ξ,φ) могут быть выражены все усилия и перемещения патрубка (оболочки). Рассматривается случай, когда длина патрубка в несколько раз превышает его диаметр. Тогда, согласно принципу Б. Сен-Венана, для исследования краевого эффекта в сочленении внешнюю нагрузку на свободном конце патрубка можно распределить

по произвольному закону, в частности, по закону синуса. Задача решалась методом сил [2], в результате для определения максимального момента в сочленении трубки с пластиной получена формула:

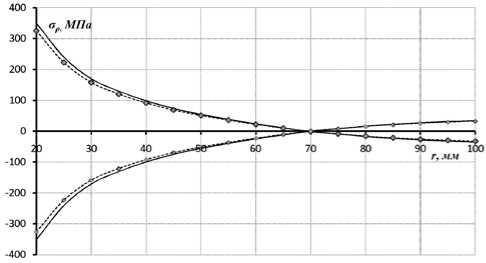
Рис. 2. Распределение нормальных напряжений по радиусу пластины

^тах =

Р1        р

^R ‘ »+v^^}(^ ) 3

Здесь для удобства практического расчёта величины момента были введены безразмерные параметры α, β и γ, графики которых представлены ниже на рис 4. В зоне сочленения напряжения на внешней и внутренней поверхностях патрубка при φ=0 будут равны

тах _ । 6М_тах   ¹ /          ^р 1 \

^  -± 52 ⁺ Rs V^ max -^

Знак «плюс» перед первым членом в этой формуле ставится при вычислении напряжений во внутренних волокнах трубки, знак «минус» – в наружных. Максимальные напряжения в пластине вычисляются по формуле

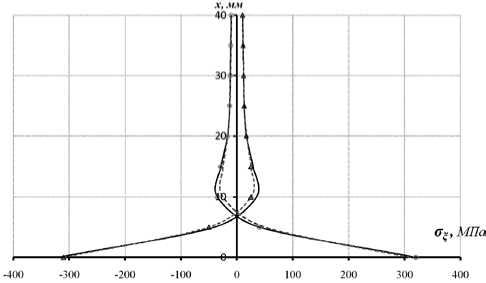
Рис. 3. Распределение нормальных напряжений по образующей патрубка

у тах _— I ^6м та.х

По полученным данным был произведён числовой расчёт для стального образца с размерами R =20 мм, R 1 =105 мм, δ =1,5 мм, l =180 мм при действии силы P =100 Н. Величина максимального изгибающего момента в сочленении трубки с пластиной, определяемая по формуле (2), равна M max =1,24∙10² Н. Этому значению момента соответствуют напряжения в сочленении по формулам (3) и (4): о ^тах - -336 МПа, а ^тзс - ±331 МПа.

На рис. 2 и 3 приведены графики напряжений σ ξ и σ ρ в плоскости изгиба системы для наружной и внутренней поверхностей образца при указанных нагружениях. Маркерами показаны экспериментальные значения напряжений, полученные при помощи проволочных тензометров с базой 5 мм.

Результаты расчёта сочленения методом конечных элементов, приведенные на рис. 2 и 3, хорошо согласуются с аналитическим решением. Из графиков видно, что максимальные напряжения возникают в месте сочленения и получаются равными у ^тах - -338,15 МПа, о^ - ±338,17 МПа. Величина максимального изгибающего момента в сочленении трубки с пластиной равна М max =1,25·10² Н.

Рассмотрен случай, когда к свободному концу патрубка (рис. 1б) вдоль образующих приложена равномерно распределённая нагрузка, равнодействующая которой равна P1. Тогда по контуру сочленения действует уже постоянный момент М1. Для его определения, так же как и в предыдущем случае, применим метод сил. Коэффициенты канонического уравнения определяются из решения уравнения осесимметричного изгиба цилиндрических оболочек и круглых пластин. Ниже приведена окончательная формула для нахождения величины погонного изгибающего момента в сочленении патрубка с пластиной:

Графики безразмерных коэффициентов α 1 , β 1 , γ 1 представлены ниже на рис. 4.

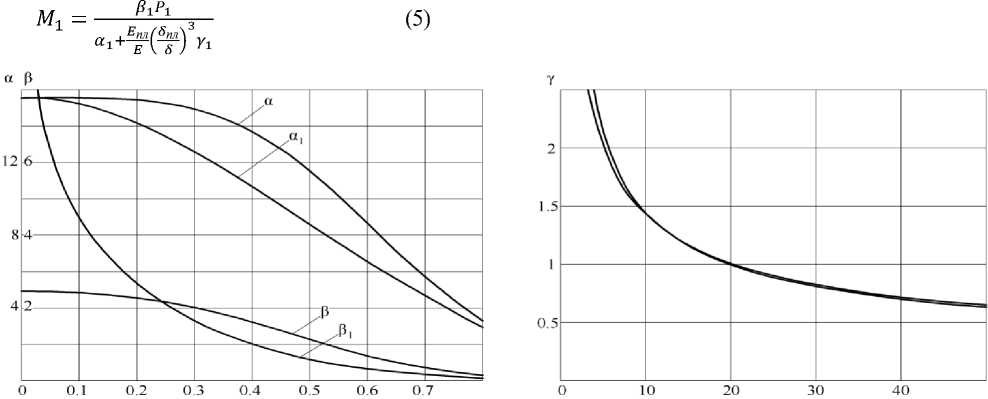
Рис. 4. Графики для определения параметровα, α 1 , β, β 1 и γ=γ 1

Максимальные напряжения в трубке и пластине у сочленения равны

„ max _     ^p i । ^6Mi

°  = - 2^5 ±               (6)

° m ^ax = 6^ 1 ,                         (7)

Максимальные напряжения в трубке определяются по формуле

max ° ?

-^^ + 6М о

25 + 5²

Знак «плюс» берётся при определении напряжений во внутренних волокнах трубки, а знак «минус» – для её наружной поверхности. По полученным формулам (5-7) проведен числовой расчёт образца, размеры которого приведены выше, а сила P 1 = 100 Н. Величина изгибающего момента в сочленении оказалась равной M 1 =17,8 Н, а максимальные напряжения (в месте сочленения патрубка с пластиной) составляют ^ т^ = —47,76 МПа и о т ^ах = 47,23 МПа. Для сравнения, как и в предыдущем случае нагружения, был проведен расчёт методом конечных элементов. Значения максимальных напряжений, полученные на основе конечно-элементной схемы, составляют ° m ^ax = -47,78 МПа и ° m ^ax = 47,48 МПа. Это также

достаточно хорошо согласуется с результатами вычислений по формулам (5-7).

Рассмотрен случай наличия в системе избыточного давления p (рис. 1в). Величина погонного изгибающего момента в сочленении вычисляется по формуле

Мо =

—pR2

So-nPi-^ (^f )\ “1+^ (^f ^{) 3}У1

График коэффициента β 0 (ρ 1 ) представлен в работе [1], величина 6₀ ( 5 ) вычисляется по формуле

е0

1,095

.

где p – избыточное давление.

Для рассмотренного выше образца при p=0,01 МПа получены значения M 0 = - 5,295 Н и ° m ^ax = —14,386 МПа. При расчёте методом конечных элементов получены значения M 0 = ‒4,956 Н и ° m ^ax = —13,861 МПа. С помощью формул (2) и (5) проведены исследования влияния некоторых геометрических параметров конструкции на напряжённое состояние соединения. Установлено, что наружный диаметр пластины не оказывает существенного влияния на величину изгибающего момента M_max . Поэтому эти формулы могут быть использованы для исследования краевого эффекта в патрубках, приваренных к корпусным элементам малой кривизны весьма произвольных очертаний. Исследования показывают также, что увеличение толщины пластины приводит к существенному снижению изгибающего момента в сочленении. Этот вывод в равной степени касается нагружения силой Р , силой Р 1 и давлением р , что позволяет при анализе более сложных конструктивных схем ограничиться рассмотрением осесимметричной задачи. Итак, изгибающий момент в сочленении патрубка с пластиной, обусловленный краевым эффектом, существенно снижается с ростом толщины пластины, максимальный момент достигается при δ пл =δ, но увеличение толщины всего корпуса изделия, снижая изгибные напряжения в сочленении, не всегда оправдано, так как связано с чрезмерным увеличением массы конструкции.

Проводились исследования напряжённого состояния сочленений в тех случаях, когда патрубки или элементы трубопроводов соединялись с тонкостенными корпусными элементами в виде

цилиндрических или сферических оболочек. Рассматривались нагружения силами, как вдоль оси патрубка, так и в поперечных направлениях. Особенности решений во всех случаях были подобны рассмотренным выше, когда корпусные элементы моделировались круглыми пластинами. Результаты исследований позволяют сделать важный вывод о том, что при увеличении радиусов кривизны цилиндрических и сферических оболочек значения изгибающих моментов в сочленении возрастают, приближаясь к той величине момента, который возникает в случае патрубка, сочленённого с пластиной.

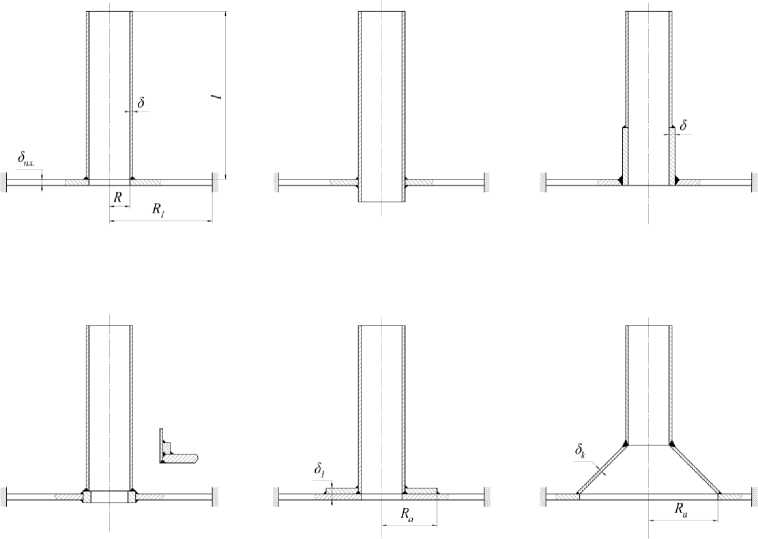
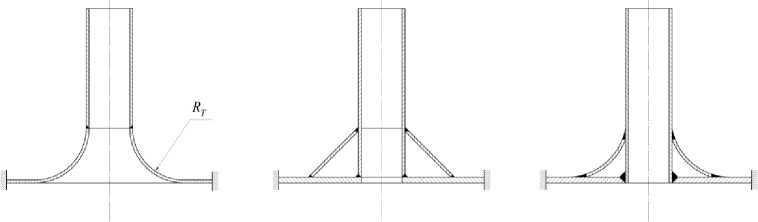
Рис. 7. Конструктивные схемы сочленений, обеспечивающие снижение уровня максимальных напряжений (варианты б - и), а также равнопрочность элементов сочленений (варианты г, д, е)

С целью снижения уровня напряжений в сочленениях патрубков с тонкостенными корпусными элементами, а также обеспечения равнопрочно-сти их элементов разработаны различные конструктивные схемы сочленений (рис. 5). Эффективность их применения исследовалась на моделях корпусных элементов с помощью аналитических решений. Эффективность представленных на рис. 5 конструктивных схем оформления сочленений подтверждена результатами усталостных испытаний до разрушения. Данные испытаний, приведённые на рис. 6 и 7, показывают, что для всех образцов нагрузки, приводящие их к разрушению, в значительной мере увеличиваются по мере снижения уровня максимальных изгибных напряжений в элементах сочленений. Это отмечено для образцов, отличающихся толщиной корпусного элемента (рис. 6).

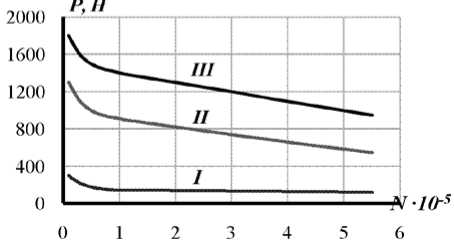
Рис. 6 . Характеристики усталостных разрушений образцов, представленных на рис. 5а (I – δ пл =1,5 мм, II – δ пл =3,0 мм, III – δ пл =5,0 мм)

Наличие накладки (рис. 7) также приводит к повышению усталостной прочности. Особо следует отметить эффективность введения конического переходного участка. Из сравнения кривых видно,    ¹

что при равной толщине корпусных элементов (δ пл =1,5 мм) наличие конического переходного участка резко увеличивает выносливость системы,   ₂

причём с увеличением радиуса большего основания конуса R 2 усталостная прочность повышается.

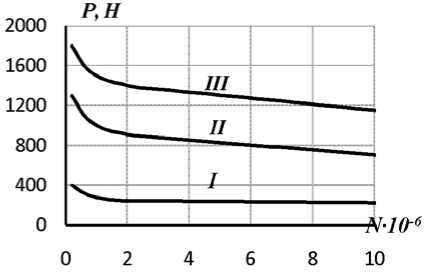
Рис. 7 . Характеристики усталостных разрушений образцов, представленных на рис. 5д (II – δ 1 =5,0 мм, I – R 2 =45 мм, III – R 2 =55 мм)