Контактная задача для двух струн с переменными натяжениями

Струна является одним из классических объектов математической физики [1]. С точки зрения механики, струна - простейший из тонкостенных объектов, к которым относятся также стержни, балки, пластины и оболочки. Для таких объектов, как и для «трехмерных» тел, могут быть рассмотрены контактные задачи [2-7]; для струн такие задачи не являются еще в достаточной мере исследованными. В [6] построено аналитическое решение контактной задачи для системы произвольного числа струн, аналогичной многолистовой рессоре как системе балок. В [7] построено в частном случае аналитическое решение задачи о контакте струны и твердого тела.

В настоящей работе рассматривается обобщение задачи [6] для двух струн; оно состоит в том, что натяжения струн являются переменными и непрерывными. Такая модель струны не является стандартной [1], но допускает наглядную интерпретацию (см. ниже). В работе сформулирована строгая постановка соответствующей контактной задачи, доказана единственность решения и построены аналитические решения в некоторых частных случаях. Этим построением одновременно доказывается существование решения.

Струна с переменным непрерывным натяжением

Рассмотрим малые статические поперечные перемещения струны в плоскости; левый конец струны закреплен; правый - свободен (рис. 1); L >  0 - длина струны. Из стандартной теории

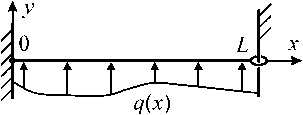
Рис. 1. Струна с закрепленным и свободным концами

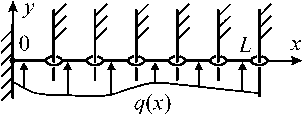
Рис. 2. Составная струна

(уравнение равновесия: Ту ‘ = - q ; краевые условия: у (0) = 0, у '( L ) = 0; см. [1, с. 29, 44]) следует, что форма у ⁽¹⁾( x ) струны под нагрузкой имеет вид:

у ⁽¹⁾⁽ x ) = L x ^f -4г L^L( ⁽ t ) dt ) ds ,

0 v T(1) s J где q(x) - плотность нагрузки, T(1) > 0 - (постоянное) натяже- ние струны. Продольными перемещениями точек струны (за счет поперечной нагрузки) пренебрегаем, так как они являются величинами более высокого порядка малости (по параметру qL/T) чем у. Пусть теперь под той же нагрузкой находится струна, состоящая из N звеньев длины L/N каждое (рис. 2) с натяжениями Т(i) = Т (iL/N), где 1 < i < N , Т(x) > 0 - некоторая непрерывная функция. Тогда нетрудно установить, что lim у(N)(x) = у(x), где у(N)(x) - форма N ^^

составной струны

7 1 г Л

Г x 1 Г L z х . I .

y ^{( x} ) = J о тгтт! s q ⁽ t ) ^dt I ^ds •

V T ⁽ s )             7

Такую получающуюся предельным переходом N ^^ систему и будем считать струной с переменным непрерывным натяжением T ( x ), изображая ее так же как на рис. 1 (без показа деления на звенья).

Постановка контактной задачи

Рассмотрим две струны с переменными непрерывными натяжениями (рис. 3); L 1 >  L ₂ - длины струн; T 1 ( x ), T ₂( x ) - натяжения струн; нагрузка приложена к нижней струне. В отсутствие нагрузки струны плотно прилегают друг к другу (на рис. 3 струны для наглядности показаны разнесенными по вертикали). Трение между струнами отсутствует. Из (1) следует, что формы струн имеют вид:

y 1 ⁽ x ) = J,

x

f 1

⁰ ( T i ( s )

I f ¹ q ( t ) dt - [ ² f ( t ) dt \ J s                J s             )

ds ,

У 2 ⁽ x ) = I

x

( 1

⁰ ( T 2 ( s )

I f   f (t) dt ds,

J s

где f ( x ) - плотность сил взаимодействия струн. Задача заключается в отыскании f ( x ). Будем считать, что эта функция имеет вид

P ⁽ x ) ⁺ S _iP i ^{5 (} x ^- xi ),

где p(x) > 0 - кусочно-непрерывна, непрерывна слева при 0 < x < L 2 и непрерывна справа при x = 0 ; Pi > 0 ; xi > 0 (все xi различны); сумма конечна; 5 - дельта-функция Дирака. Обозначим r(x) = y 2 (x) - y 1(x) (расстояние между струнами). Из (2), (3) следует, что x         L 2

r ( x ) =     a ( s )       f ( t ) dt - k ( s ) ds ,

0          s где a (x) = I/ T1 (x) +1[ T2 (x), k (x) =

1 + T 1 ( x)( T 2 ( x )

[ ¹ q ( s ) ds . x

Будем считать, что q ( x ) >  0 непрерывна при 0 <  x <  L 1 , а T 1 ( x ) и T ₂( x ) непрерывно дифференцируемы при 0 <  x <  L ₂; тогда k ( x ) >  0 непрерывно дифференцируема при 0 <  x <  L ₂. Условие контакта струн состоит, помимо неотрицательности плотности сил взаимодействия, в том, что расстояние между струнами неотрицательно, а в тех точках, где плотность сил

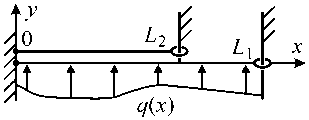
Рис. 3. Контакт двух струн

взаимодействия положительна, - равно нулю. Окончательно, приходим к следующей математической постановке задачи.

Задача . Найти функцию f ( x ) вида (4) такую, что при 0 <  x <  L ₂

= 0 ( f ( x ) >  0),

> 0 (f (x) = 0), где r(x) выражается формулой (5), в которой a(x) > 0 непрерывна при 0 < x < L 2, k(x) > 0 непрерывно дифференцируема при 0 < x < L 2 .

Доказательство единственности решения

Утверждение 1 . Поставленная задача может иметь только одно решение.

Доказательство. Пусть f ( x ) и f * ( x ) - два решения задачи. По формуле (5) им соответствуют функции r ( x ) и r * ( x ). Обозначим

^( X) = f (X) - f * (X).(7)

Так как f ( х ) и f * ( х ) имеют вид (4), то ^ ( х ) также имеет вид (4), но p ( х ) и P i в (4) могут быть неположительными. Обозначим

E = J02 (r(х) - r*(х))^(х)dx.

Из (6), (7) нетрудно установить, что в (8) подынтегральная функция неположительна; следовательно, E <  0. C другой стороны, подставляя (5) в (8) и учитывая (7), найдем

E = j 2 a(х) J2 (х)dx,(9)

где

J(х) = L 2 ^(s) ds .(10)

x

Из (9) следует, что E >  0. Так как выше было доказано неравенство E <  0, то E = 0 . Далее, учитывая (10) и упомянутый выше вид ^ ( х ), легко установить, что из (9) и равенства E = 0 следует, что J ( х ) = 0 при 0 <  х <  L ₂. Тогда ^ ( х ) = 0 при 0 <  х <  L ₂. Действительно, ^ ( х ) = p ( х ) + ^ _iP i S(. х - x_i ); предположим, что p ( х ) >  0 при некотором х * > 0. Тогда, в силу непрерывности p ( х ) слева и конечности суммы, можно найти такие Е 1 > Е ₂ >  0, что отрезок 0 <  х * - Е 1 <  х <  х * - е ₂ не содержит ни одной точки x_i и p ( х ) >  0 на этом отрезке; это противоречит равенству J ( х ) = 0 при 0 <  х <  L ₂ . Аналогично устанавливается невозможность неравенств p ( х ) <  0 при х >  0 и p (0) ^ 0; следовательно, p ( х ) = 0 при 0 <  х <  L ₂, откуда ^ ( х ) = ^ ^t^.х - x_i ). Пусть х * >  0 - максимальное из чисел x_i , соответствующих ненулевым значениям P i . Тогда из (10) следует, что J ( х ) ^ 0 в некоторой левой полуокрестности х * , что противоречит равенству J ( х ) = 0 при 0 <  х <  L ₂. Таким образом, ^ ( х ) = 0 и f ( х ) = f * ( х ) при 0 <  х <  L ₂ ; тем самым утверждение 1 доказано.

Аналитическое решение задачи в некоторых частных случаях

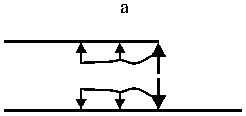
Утверждение 2. Если к‘(х) < 0 при 0 < х < L2, то решение поставленной задачи имеет вид f (х) = - к‘(х) + к (L 2Ж х - L 2)(11)

(соприкосновение по всему отрезку 0 <  х <  L ₂, рис. 4, a ).

Доказательство. Очевидно, что f ( х ) имеет вид (4). Подставляя (11) в (5), найдем, что r ( х ) = 0 при 0 <  х <  L ₂ ; таким образом, (6) выполнено.

Утверждение 3. Если к‘(х) > 0 при 0 < х < L2, то решение поставленной задачи имеет вид f (х) = F5( х - L 2)(12)

(соприкосновение в одной точке, рис. 4, b ; здесь и далее соприкосновение в точке закрепления не упоминается), где

F = Jq 2 a(х)к(х)dx j j^ 2 a(х)dx .(13)

Доказательство. Очевидно, что f (х) имеет вид (4). Подставляя (12) в (5), найдем r (х) = j a (s) (F - к (s)) ds .(14)

Из (13), (14) следует, что r ( L ₂) = 0. Так как к ‘ ( х ) >  0, то из последнего равенства вытекает, что к (0) <  F <  к ( L ₂) (иначе из (14) следует, что либо r ( L ₂) <  0, либо r ( L ₂) >  0). Тогда существует 0 <  х * <  L ₂ такое, что F = к ( х * ), и из (14) следует, что r ( х ) не убывает при 0 <  х <  х * и не возрастает при х * <  х <  L ₂ . Отсюда и из равенств r (0) = 0, r ( L ₂) = 0 вытекает неравенство r ( х ) >  0

при 0 <  x <  L ₂ . Далее, f ( x ) может быть положительно только при x = L ₂, а r ( L ₂) = 0; таким образом, (6) выполнено.

Утверждение 4 . Пусть существует 0 <  x ₀ <  L ₂ такое, что k '( x ) >  0 при 0 <  x <  x ₀, k '( x ₀) = 0 , k '( x ) <  0 при x ₀ <  x <  L ₂; тогда решение поставленной задачи имеет следующий вид:

a) если Ф (L 2) > 0 , то f (x) = F5( x - L 2) (соприкосновение в одной точке, рис. 4 b);

b ) если Ф ( L ₂) <  0 , то

f ( x ) = k ( L 2 W x - L 2 ) +

[ 0

<

- k ‘ ( x )

(0 <  x <  2 ), ( 2 <  x <  L ₂)

(соприкосновение по части отрезка 0 <  x <  L ₂, рис. 4 c ), где

Ф ( Л ) = J a ( x ) ( k ( Л ) - k ( x ) ) dx ,

x ₀ <  2 <  L ₂ - корень уравнения Ф ( Л ) = 0,                   (18)

F выражается формулой (13).

Доказательство

• a )    Очевидно, что f ( x ) имеет вид (4). Подставляя (15) в (5), найдем для r ( x ) выражение (14). Из (13), (14) следует, что r ( L ₂) = 0. Из (13), (17) и условия Ф ( L ₂) >  0 следует, что F <  k ( L ₂) . Из

свойств функции k ( x ) тогда вытекает, что F >  k (0) (иначе из (14) следует, что r ( L ₂) <  0). Из этих же свойств тогда следует, что существует 0 <  x * <  x ₀ такое, что F = k ( x * ); рассуждая затем так же, как при доказательстве утверждения 3, получим, что r ( x ) >  0 при 0 <  x <  L ₂ и условия (6)

выполнены.

• b )    Существование корня x ₀ <  2 <  L ₂ следует из непрерывности Ф ( Л ) при x ₀ < Л <  L ₂ и зна

чений Ф(x 0) > 0 (так как функция k(x) достигает максимума в точке x0), Ф(L2) < 0; единст венность корня следует из утверждения 1. Так как k‘(x) < 0 при x 0 < x < L 2, а 2 > x 0, то f (x)

имеет вид (4). Подставляя (16) в (5), найдем с учетом (17), (18)

r ( x ) = <

J a ( s ) ( k ( 2 ) - k ( s ) ) ds

(0 <  x <  2 ), ( 2 <  x <  L 2 ).

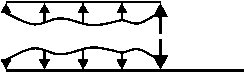
Заметим, что k ( 2 ) >  k (0); действительно, если k ( 2 ) <  k (0), то, в силу свойств функции k ( x ), k ( 2 ) <  k ( x ) при 0 <  x <  2 ; тогда из (19) следует, что r ( 2 ) <  0, тогда как r ( 2 ) = 0. Из неравенства k ( 2 ) >  k (0) следует, что существует 0 <  x * <  x ₀ такое, что k ( 2 ) = k ( x * ); рассуждая затем так же, как при доказательстве утверждения 3, получим, что r ( x ) >  0 при

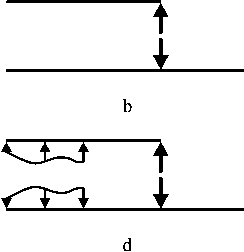
Рис. 4. Варианты сил взаимодействия в системе двух струн 0 < x < L2 . Далее, f (x) может быть поло жительно только при 2 < x < L2 , а на этом отрезке r(x) = 0; таким образом, (6) выполнено.

Утверждение 5 . Пусть существует 0 <  x ₀ <  L ₂ такое, что k ‘ ( x ) <  0 при 0 <  x <  x ₀ , k '( x ₀) = 0 , k ‘ ( x ) >  0 при x 0 <  x <  L ₂ ; тогда решение поставленной задачи имеет следующий вид:

a) если Т (0) < 0, то f (X) = F5( x - L 2)

(соприкосновение в одной точке, рис. 4, b). b) если У(0) > 0, то f (x) = k (д)5( x - L 2) + <

'- к ‘ ( X )

(0 <  x <  д ),

⁽ Д <  ^x <  L 2 ),

(соприкосновение по части отрезка 0 <  x <  L ₂ ив точке, рис. 4, d) , где

У ( М ) = j М ² a ( x ) ( к ( М ) - к ( x ) ) dx ,

0 <  ц <  x 0 - корень уравнения У ( М ) = 0, F выражается формулой (13).

Доказательство аналогично доказательству утверждения 4 и поэтому здесь не приведено.

Некоторые замечания к полученным результатам и выводы

Можно показать, что утверждения 1-5 остаются справедливыми и при заметном ослаблении требований на гладкость функции к ( x ). Эту функцию можно считать лишь кусочнонепрерывной и кусочно-непрерывно дифференцируемой, если понимать к ‘ ( x ) в «обобщенном смысле»: в точках излома к ( x ) доопределять к ‘ ( x ) по непрерывности слева, а в точках разрыва к ( x ) (первого рода) добавлять к к ‘ ( x ) соответствующую 5 -функцию.

Использованный подход к постановке и решению контактной задачи для двух струн может быть применен как для дальнейшего исследования данной задачи (случаи, когда к ‘ ( x ) меняет знак более одного раза), так и для решения близких контактных задач (для балок).