Контактная задача о кручении круглым штампом трансверсально-изотропного упругого полупространства с неоднородным трансверсально-изотропным покрытием
Автор: Васильев Андрей Сергеевич, Садырин Евгений Валерьевич, Федотов Игорь Александрович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 1-2 (70-71) т.13, 2013 года.
Бесплатный доступ
Рассмотрена осесимметричная контактная задача теории упругости о кручении круговым штампом трансверсально-изотропного полупространства с неоднородным покрытием. С помощью техники интегральных преобразований решение задачи сведено к решению интегрального уравнения. Построено явное выражение трансформанты ядра интегрального уравнения для однородного трансверсально-изотропного покрытия. Предложена схема численного построения трансформанты ядра в случае произвольного закона изменения модуля сдвига по глубине покрытия. Используя аппроксимацию трансформанты ядра некоторыми специальными функциями, построено двухсторонне асимптотически точное приближённое аналитическое решение задачи. Проанализирован частный случай изменения модулей сдвига в трансверсально-изотропном покрытии, позволяющий построить явное замкнутое решение задачи. Численно исследуется модельная задача о кручении биоматериала. Считается, что покрытие представляет собой хрящевую ткань, а свойства подложки соответствуют кортикальной кости.
Контактные задачи, теория упругости, кручение, неоднородность, анизотропия
Короткий адрес: https://sciup.org/14249957
IDR: 14249957 | УДК: 539.3
Текст научной статьи Контактная задача о кручении круглым штампом трансверсально-изотропного упругого полупространства с неоднородным трансверсально-изотропным покрытием
Введение. Первые работы по моделированию задачи о кручении упругого полупространства круглым штампом относятся к середине прошлого века. Задача о кручении однородного упругого полупространства круглым штампом впервые была сформулирована и решена в динамической постановке Рейснером и Сагочи [1]. В работе Снеддона [2] данная задача, с использованием техники интегральных преобразований, сведена к решению интегрального уравнения.
Грилицкий В. Д. [3] построил решение задачи о кручении круглым штампом изотропной двухслойной среды и ортотропного упругого слоя в виде ряда по степеням б 1, где б — отношение толщины первого слоя к радиусу штампа. Kassir М. К. [4] построил решение задачи о кручении неоднородного изотропного полупространства в случае степенного изменения модуля сдвига по глубине. Решение задачи для изотропного полупространства с неоднородным покрытием при произвольным законе изменения модуля сдвига по глубине получено Айзиковичем С. М. [5]. Erguven М. Е. рассмотрел задачу о кручении трансверсально-изотропного упругого полупространства с однородным покрытием [6].
Задача активно изучается по настоящее время, в частности, Wang Y.-S. использовал кусочно-линейную аппроксимацию трансформанты ядра для сведения задачи к решению интегрального уравнения [7]. В работе [8] решена задача о кручении трансверсально-изотропного пьезоэлектрического однородного полупространства.
В настоящей работе построено решение контактной задачи о кручении трансверсальноизотропного упругого полупространства с неоднородным трансверсально-изотропным покрытием при произвольном изменении упругих свойств по глубине покрытия.
Изменение механических свойств по одной из координат и анизотропия упругих свойств характерны для многих тел, как в природе, так и в технике. В технике неоднородность и анизотропия связаны с условиями создания и эксплуатации деталей машин. Большинство биологических объектов являются неоднородными и анизотропными, что свидетельствует об актуальности построения математических моделей, учитывающих одновременно и неоднородность, и анизотропию.
Постановка задачи. Недеформируемый круглый штамп с плоским основанием жёстко сцеплен с верхней гранью Г упругого неоднородного трансверсально-изотропного полупространства Q. С полупространством связана цилиндрическая система координат r.tp.z. Штамп контактирует с полупространством по поверхности z = 0, г < а
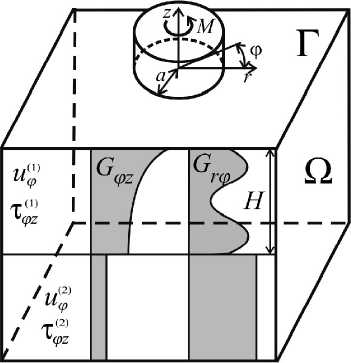
Рис. 1. Задача о кручении
К штампу приложен крутящий момент М, ось которого совпадает с осью z (рис. 1). Под действием этого момента штамп повернётся относительно оси z на угол г, вызвав деформацию кручения Q. Модули сдвига G^, ^полупространства с глубиной изменяются по законам:
J
fr,^ -H
где f^, f^z — некоторые функции, определяющие закон изменения модулей сдвига в покрытии, причём f^ — непрерывная, a f^z— непрерывно дифференцируемая; параметры Pi, р2 задают скачок упругих свойств на границе покрытие-подложка.
Вне штампа поверхность Г не нагружена. При сделанных предположениях граничные условия задачи имеют вид z = 0: о = т = О,
1^=0, r>a К = ге, г < а."
Учитывая, что слой подвержен лишь деформации скручивания, ненулевым является лишь смеще^
ние вдоль оси ср uz=ur =0, u^u^r.z^
Напряжения, в соответствии с законом Гука, примут вид о =а =а =т =0,т = G (z)^-,t =G
Введём обозначения
r^,-H
z<-H, W’, z<-H tpz' ' Ф '
При г ^ да и z -> -оо напряжения исчезают. Считаем, что перемещения и напряжения сопряга ются на границе изменения закона неоднородности:
z =—Н : т(1) = т(2), и№ = и®
• • ■ CpZ pz' wp
Требуется определить закон распределения контактных касательных напряжений под штампом т^ко = тД/-), г<а.
Сведение задачи к решению интегрального уравнения. Уравнения равновесия при данной постановке принимают вид:
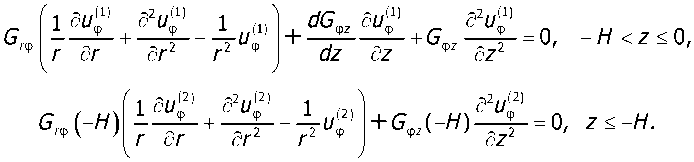
Для сведения задачи к решению интегрального уравнения используем интегральное преобразование Ханкеля:
u?(r,z) = jte^zp^ry^cV, J =1,2. (7)
о
Обозначим
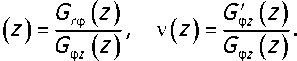
Подставив (7), (8) в (5) и (6), и приравнивая к нулю в полученных соотношениях подынтегральные выражения, получим систему обыкновенных дифференциальных уравнений относительно функций U, (y,z), j =1,2 :
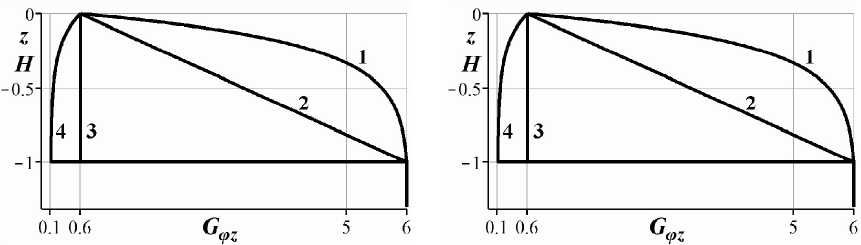
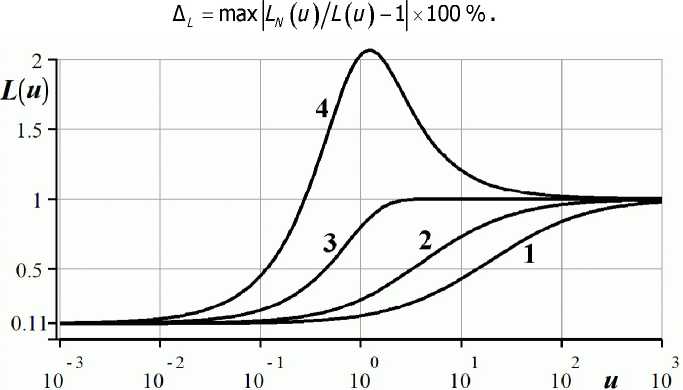
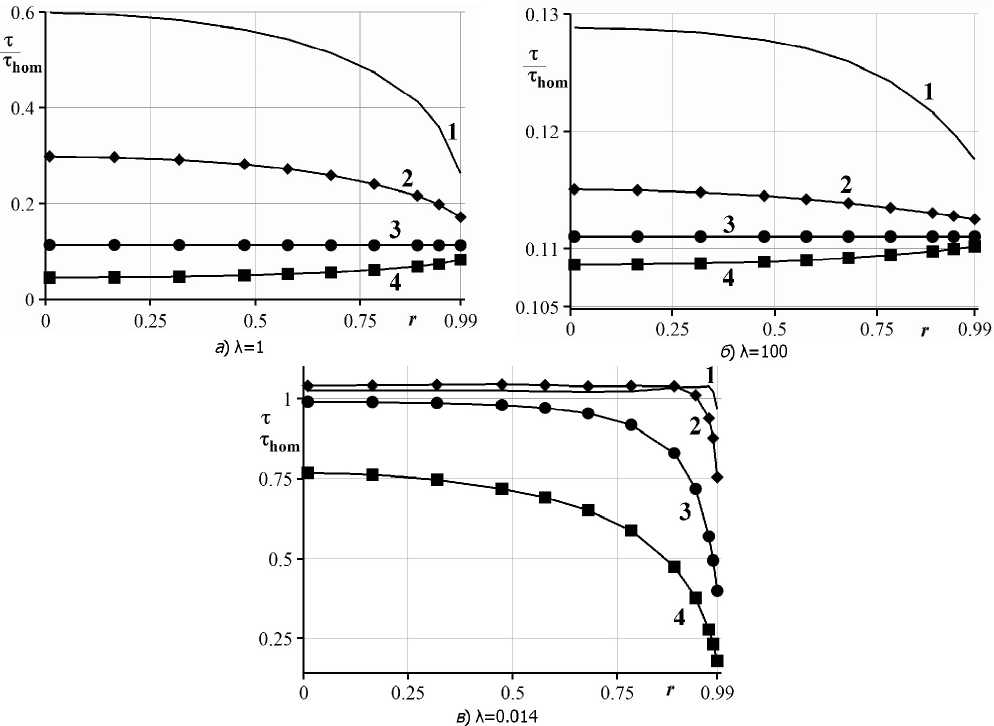
(/1"(Y,z) + v(z)(/i'(y,z)-y2k(z)(/1(y,z) = 0, -H ^2(y,z)-Y2k(-^)^2(y,z) = 0, -/ Общее решение уравнения (10) имеет вид: U, (Y,z) = В, (¥)е-'*й +В, (Yle--^. Из условия ограниченности перемещений при z -> -оо имеем в2 (у) = 0, тогда £/2(Y,z) = F1(Y)e¥Z^.(11) Условия сопряжения (4) можно записать в виде: ц(у,-и) = и.^,-ну и^.-н) = №^,-ну Или, используя явный вид функции (/2 (y,z) (11), получим: Из (3) при z= 0 и (7) следует: (/1'(y,0) = T(y)K(0). (13) Здесь Ду) связана с та (г) преобразованием Ханкеля 7(y) = JTa (р)Л (py)P^P ■ О Введём вспомогательную функцию Uy (y,z): Щ (y,z) = уЦ (y,z)7 1 (у) ДД0)М0) ■(15) Ввиду однородности, уравнение (9) относительно функции Uy (y,z) не изменится. Условия (12), (13) относительно Uy примут вид 2 р у ,(16) иД^-н^ ’ (/1'*(y,0) = y7k(0)-(17) Далее U^,^ будем обозначать Г (у). Затем, используя условие (2), можно записать интегральное уравнение нашей задачи: иф U=j^i (Y, 0) Л (гу)у^у = ? Jr (y)T(у) Л Hehl = гг, r 0 а/^ф^^фЛ0) 0 Используя (14), уравнение можно представить в виде: JL (р)pjГ (у)Л (гу)Л(py)t/yt/p = гг^ДО^ДО), г<а. о о Сделаем замену переменных: Нч = и, К = Н]а, г' = г/а, р' = р/а ,L(iA = 1Ди/НА, Др'А = т Др'аА. Далее штрихи опускаем, тогда интегральное уравнение задачи примет вид: 1 со ________________________________ jT^pjLjvp^rA^J^pA1)^^ г <1. (18) о о Таким образом, для построения интегрального уравнения задачи необходимо построить функцию Uy (у,0) из краевой двухточечной задачи (9), (16), (17). Построение трансформанты ядра интегрального уравнения. Для некоторых частных случаев изменения модуля сдвига в покрытии удаётся получить явное выражение для трансформанты ядра U Например, для покрытия, в котором модули сдвига постоянны: /^С ^гер' z^S [^гер/ Gc , G5 , В этом случае решение уравнения (9) можно построить в явном виде, и трансформанта ядра принимает вид: r2uH5v ~5uH\ Gc5,-Gs5. Gc u = ф21__ »z2 5 = 222 5 M Gc 6, + GS5, 1\GC 2 v(pzvl ipz2 1 Заметим, что для многослойной среды уравнение (9) распадается на /V независимых дифференциальных уравнений с постоянными коэффициентами, для каждого из которых известно явное решение. Для построения значения трансформанты ядра в некоторой точке достаточно решить систему линейных алгебраических уравнений. Для произвольного закона изменения модуля сдвига по глубине значение трансформанты ядра может быть получено численно. Введём обозначения: Уравнение (9) перепишем в виде линейной системы обыкновенных дифференциальных уравнений первого порядка: J оо[ = оо2 |оо2 = -v(z)oo2 +^ или в матричной форме: 00 = 1 (оо2 — = Асо, - К < z< 0, А dz Краевые условия (16), (17) принимают вид: “г^!1V-н = ₽2yJk Решение краевой двухточечной задачи при фиксированном у построим, используя метод моделирующих функций [9], предложенный для построения трансформант ядер динамических контактных задач. Ищем оо (у,z) в виде: w(Y,z) = B1(y)a(Y,z)evz. Вектор 3(y,z) определяется из задачи Коши при фиксированном y: da А - - ,, n — = Aa-ya, -H Затем, используя второе условие (19), находим В^ (y) и тем самым оох (у,0): Аналогично работе [10] можно показать, что трансформанта ядра £(ц) обладает свойствами: 1(0) = G (0)6 (0) пр Vм/^pz Vм/ Л г* / U \ г* / Ц\ 1 \СгД-Н)СфД-Н) Построение решения задачи. Будем говорить, что функция /(и) принадлежит классу П№ где /V— натуральное число, если она представима в виде: /V и2+ Д2 f ^= A. А еС,А^ А^В; # В] при i #j. /=1 и + D, Для трансформанты ядра LN(u^er\N можно построить [11] решение интегрального уравнения (18) в форме: ^хО1М°) где постоянные С, определяются из системы линейных алгебраических уравнений: /v ( Д D Л 1 + Я Л 1 h ' U Л J £ж(0)52А-2 ' ' ' ' Здесь использованы обозначения: shAr rshA ch Atdt p(A5) = (AchA + 5shA)/(52 - А2). Таким образом, для построения решения исходной контактной задачи достаточно аппроксимировать трансформанту ядра интегрального уравнения функцией класса П№ Для построения аппроксимации можно использовать алгоритм, описанный в работе [11], где показано, что решение (21) является асимптотически точным при Л^О и Л^оо. Решение задачи для частного случая изменения модулей сдвига. Пусть для модулей сдвига выполнены равенства: = const, 31 = p2=l. Тогда первое равенство (8) можно переписать в виде: ^ = Gr^jc. Учитывая (23), уравнение (9) принимает вид: +gT^"^g-^(v'z| = °- "н '25°- Общее решение уравнения (24) имеет вид: l/1-(v,z) = c1(v)eFl*1i<2(v)e^^ где F(z)=jG„(z)dz. Продифференцируем U^,z^ noz: Тогда из краевого условия (16), учитывая (23), следует: с2(у) = о. Из краевого условия (17) и равенств (23), (26) получаем следующее: С =1 Из (25), (26), (27) следует, что для любого у выполнено тождество U^\,O>1. Тогда £(«) = !. Таким образом, если для модулей сдвига трансверсально-изотропного полупространства с неоднородным трансверсально-изотропным покрытием выполнены равенства (22), то трансформанта ядра интегрального уравнения тождественно равна единице. Следовательно, решение задачи совпадает с решением для однородного полупространства с модулем сдвига равным си имеет вид: Численные примеры. Рассмотрим трансверсально-изотропную упругую подложку с модулями сдвига^ (-Н) = 5, (j(pz(-H) = 6 и пусть модули сдвига на поверхности покрытия равны 6?,р (0) = G„z (0) = 0,608. Такие значения модулей сдвига соответствуют свойствам хряща (покрытие) и кортикальной кости (подложка). Предположим, модули сдвига покрытия изменяются по одному из следующих законов: 1. frip (z) = 5,03 - 4,422е52/я, fvz (z) = 6,037 - 5,428е52/я ; 2. frp (z) = 0,608 - 4,392 z/H, f^ (z) = 0,608 -5,392z/H ; 3. f,p (z) = fpz (z) = 0,608; 4. f,p(z) = fpz(z) = 0,118 + 0,489e52/". Эти законы описывают трансверсально-изотропные покрытия, модули сдвига которых возрастают экспоненциально (закон 1) и линейно (закон 2); однородное изотропное покрытие (закон 3) и изотропное покрытие (закон 4), упругие свойства которого экспоненциально убывают, а на границе покрытие-подложка наблюдается скачок модулей сдвига G^, GpZ в 41 и 49 раз соответственно (31=41, 32=49). Графики изменения модулей сдвига по глубине для законов 1—4 изображены на рисунке 2. Рис. 2. Изменение модулей сдвига по глубине в материалах 1—4 Трансформанты ядер, соответствующие покрытиям 1—4, изображены на рисунке 3. Построены аппроксимации трансформант ядер функциями класса П/v, их погрешности равны 0,8 %, 0,82 %, 0,64 % и 0,49 % соответственно. Под погрешностью аппроксимации понимаем следующее выражение: Рис. 3. Трансформанты ядер для материалов 1—4 Введём величину тге, (Л,г) = т(Л,г)/тЬот(г) где Л = Н/а — геометрический параметр задачи, характеризующий относительную толщину ПО' крытия; т(Л,г) — контактные напряжения под штампом для рассматриваемой неоднородной среды; Thom (г) — контактные напряжения однородной изотропной среды с модулем сдвига, равным .^СД^бД^. Величина тге| характеризует распределение контактных касательных напряжений под штампом для неоднородной среды по сравнению с однородной средой. Графики величины тге| для материалов 1—4 в случае относительно толстого покрытия (Л=100), тонкого покрытия (Л~1/100) и покрытия, сравнимого по размерам с размерами штампа (Л=1), изображены на рисунке 4. Из графиков видно, что неоднородность покрытия оказывает существенное влияние на решение контактной задачи, особенно для покрытий малой толщины. Наиболее существенное перераспределение контактных напряжений по сравнению со случаем однородного полупространства наблюдается на краю штампа (г-^1). Рис. 4. Контактные напряжения для законов 1—4 Заключение. Построено приближённое аналитическое решение контактной задачи о кручении трансверсально-изотропного упругого полупространства с неоднородным трансверсальноизотропным покрытием, эффективное для любых относительных толщин покрытий (значений параметра Л). Показано, что в случае, когда модули сдвига трансверсально-изотропного полупространства изменяются в соответствии с условием (22), распределение контактных напряжений под штампом совпадает со случаем однородного изотропного полупространства. На основании высокой точности аппроксимации трансформант ядер интегральных уравнений (менее 0,8 %) можно утверждать о малой погрешности построенных решений контактной задачи даже для покрытий сложной структуры (материал 4). Построенное в работе решение позволяет исследовать одновременное влияние анизотропии и неоднородности покрытия на механические характеристики контактного взаимодействия. Результаты актуальны для широкого класса современных полимерных, биологических и композиционных материалов.
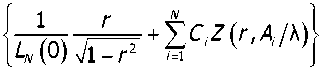
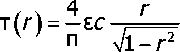
Список литературы Контактная задача о кручении круглым штампом трансверсально-изотропного упругого полупространства с неоднородным трансверсально-изотропным покрытием
- Reissner, E. Forced torsional oscillations of an elastic half-space/E. Reissner, H. F. Sagoci//Journal of Applied Physics. -1944. -Vol. 15. -№ 9. -Pp. 652-654.
- Sneddon, I. N. The Reissner-Sagoci problem/I. N. Sneddon//Proceedings of the Glasgow Mathematical Association. -1966. -Vol. 7. -№ 3. -Pp. 136-144.
- Грилицкий, Д. В. Кручение двухслойной упругой среды/Д. В. Грилицкий//Прикладная механика. -1961. -Т. 7. -№ 1. -С. 89-94.
- Kassir, M. K. The Reissner-Sagoci problem for a non-homogeneous solid/M. K. Kassir//International Journal of Engineering Science. -1970. -Vol. 8. -№ 10. -Pp. 875-885.
- Айзикович, С. М. Кручение круглым штампом неоднородного полупространства/С. М. Айзикович//Расчёт оболочек и пластин: сб. трудов. -Ростов-на-Дону: РИСИ, 1978. -С. 156-169.
- Erguven, M. E. Torsion of a transversely isotropic elastic layer bonded to a transversely isotropic half-space/M. E. Erguven//International Journal of Engineering Science. -1986. -Vol. 24. -№ 9. -Pp. 1501-1509.
- Liu, Tie-Jun. Reissner-Sagoci problem for functionally graded materials with arbitrary spatial variation of material properties/Tie-Jun Liu, Yue-Sheng Wang//Mechanics Research Communications. -2009. -Vol. 36. -№ 3. -Pp. 322-329.
- Xiong, Su-ming. The Reissner-Sagoci problem for transversely isotropic piezoelectric half-space/Su-ming Xiong, Guang-zheng Ni, Peng-fei Hou//Journal of Zhejiang University SCIENCE A. -2005. -Vol. 6. -№ 9. -Pp. 986-989.
- Бабешко, В. А. Методы построения матриц Грина для стратифицированного упругого полупространства/В. А. Бабешко, Е. В. Глушков, Н. В. Глушкова//Журнал вычислительной математики и математической физики. -1987. -Т. 27. -№ 1. -С. 93-101.
- Айзикович, С. М. О свойствах функций податливости, соответствующих слоистому и непрерывно-неоднородному полупространству/С. М. Айзикович, В. М. Александров//Доклады академии наук СССР. -1982. -Т. 266. -№ 1. -С. 40-43.
- Айзикович, С. М. Асимптотические решения контактных задач теории упругости для неоднородных по глубине сред/С. М. Айзикович//Прикладная математика и механика. -1982. -Т. 46. -№ 1. -С. 148-158.


