Контактное взаимодействие упругих тел при наличии двух резко различных по протяженности масштабов шероховатости их границ

когда шероховатость границ взаимодействующих тел характеризуется двумя сильно различающимися между собой типичными масштабами протяжённости: Λ и λ (λ << Λ). Взаимодействующие поверхности считаются плоскими.

В нулевом приближении принимается во внимание только крупномасштабная (масштаба Λ) шероховатость и предполагается, что эффектами от мелкомасштабной шероховатости (масштаба λ) можно пренебречь, так что контакт между телами считается полным. Это допущение означает и пренебрежение толщиной некоторого эквивалентного слоя, определяемого собственно мелкомасштабной шероховатостью. Эффекты от мелкомасштабной шероховатости рассматриваются в следующем, первом приближении.

Здесь рассматривается случай, когда в абсолютно жёстком теле имеется один крупномасштабный элемент шероховатости, который представляет собой вытянутую в одном направлении впадину (выемку), моделирующую дефект в теле. Полагается, что в окрестности такого дефекта, в сечениях, нормальных к направлению его вытянутости и не близких к концам, реализуются условия плоской деформации. Допущение о пренебрежимо малой толщине эквивалентного слоя позволяет пренебречь наличием самого этого слоя и воспользоваться решением соответствующей задачи [1, 2], где рассмотрены условия, при которых в пределах дефекта возникает площадка неконтакта, показанная на рисунке 1.

Мелкомасштабная шероховатость, рассматриваемая только в первом приближении, описывается в рамках модели Гринвуда–Вильямсона [3]. Параметры модели берутся с учётом решения, полученного в нулевом приближении (о развитии модели и успешном ее применении к анализу экспериментальных данных см. в работах [4–6]).

Известно [3], что контактное взаимодействие определяется только формой зазора между контактирующими телами (их сдвиговое взаимодействие во внимание не принимается ввиду предполагаемой его малости). Тогда, без ограничения общности, можно считать шероховатой границу только одного из контактирующих тел, если при этом обеспечить соответствие профиля шероховатости зазору между недеформированными поверхностями, то есть использовать профиль эквивалентной шероховатости и приведённый модуль упругости: E * = [ (1 - v^jE 1 + (1 - v ₂²)/ E 2 ] , где E 1 и E 2 — модули упругости, v 1 и v ₂ — коэффициенты Пуассона контактирующих тел [3]. Тогда при контакте гладкой поверхности с шероховатой, но имеющей профиль эквивалентной шероховатости, площадь фактического контакта взаимодействующих тел зависит от степени их сближения, как в случае взаимодействия тел с первоначально заданными шероховатыми границами.

Основная цель проводимого здесь исследования состоит в оценке влияния возмущения напряжённого состояния, вызванного впадиной, на изменение параметров мелкомасштабной шероховатости [3]. При этом обратное влияние указанного изменения на напряженное состояние впадины считается пренебрежимо малым, что допустимо вследствие предположения λ << Λ.

Наибольший интерес представляет изменение параметров мелкомасштабной шероховатости на продолжении дефекта, где известно (из полученного в [1] решения соответствующей задачи о дефекте в виде выбоины) распределение контактного давления. Предположение λ << Λ позволяет считать какое-либо локальное значение давления на продолжении дефекта равным постоянному значению фигурирующего в модели Гринвуда–Вильямсона давления, которое получается отнесением действующего на контактирующие тела усилия к номинальной площади их контакта. Протяжённость

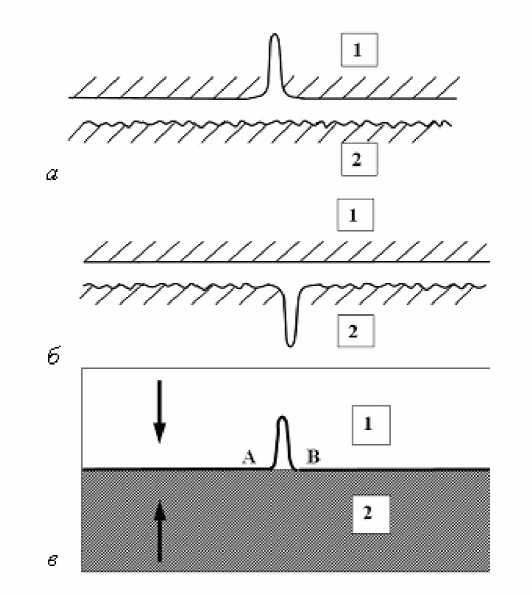
Рис. 1. Возможные схемы (а) и (б) двухмасштабной шероховатости тел с номинально плоскими границами, приводящие к появлению площадки неконтакта АВ при упругом сжатии двух тел (в): а – «жесткое» тело 1 с относительно крупной впадиной и упругое тело 2 с мелкомасштабной шероховатостью (схема рассмотрена в [1]); б – «жесткое» тело 1 и упругое тело 2 с двухмасштабной шероховатостью (схема рассмотрена в [3, 4, 7]), в – площадка неконтакта АВ при неполным проникновении упругого тела 2 в крупную впадину в жёстком теле 1

границы контакта полагается бесконечной, и все условия вдоль неё — неизменными. Задаваемым параметром внешнего воздействия в модели Гринвуда–Вильямсона является сближение между контактирующими телами, а усилие (или соответствующее давление), которое прижимает их друг к другу, находится в результате вычислений. В рассматриваемой постановке возникает обратная задача, а именно — задача отыскания сближения между контактирующими телами, которое соответствует заданной величине прижимающего их друг к другу давления. Последнее равняется локальному давлению, возникающему в задаче о дефекте в рассматриваемой точке на его продолжении. Таким образом, сначала требуется решить указанную обратную задачу, а затем при помощи её решения найти распределение сближения между контактирующими телами и распределение реальной площади контакта (осуществляемого через микроплощадки масштаба λ) на продолжении дефекта. Это те величины, по которым судят о влиянии рассматриваемого контакта на его трибологическое, электрическое или иное поведение.

• 2.    Задача о протяженной впадине (дефекте)

Рассматривается задача о напряжённом состоянии полубесконечного упругого тела, возникающем при его прижатии к жёсткому телу равномерно распределённым на «бесконечности» давлением p. В жёстком теле имеется протяженная впадина (дефект), вне которой граница жесткого тела является плоской. Упругое тело считается занимающим полуплоскость y>0. Толщина эквивалентного слоя, определяемого шероховатостью, по соображениям, изложенным во введении, не учитывается.

Искомое решение представляется в виде суммы решений двух задач: задача 1 решается при условии, что контакт имеет место всюду; в задаче 2 предполагается, что имеется площадка неконтакта, которая моделируется математическим разрезом и находится в области, где, согласно решению задачи 1, действуют в основном растягивающие напряжения. Считается, что математический разрез находится в бесконечном однородном упругом теле, в котором напряжения на бесконечности стремятся к нулю. На противоположные берега разреза действуют напряжения, равные по величине и противоположные по знаку тем, которые получаются в соответствующих местах согласно решению задачи 1. Координаты концов разреза находятся из условия непрерывности напряжений в них. В результате сложения решений обеих задач получается решение, являющееся искомым, так как оно удовлетворяет следующим условиям:

• •    берега разреза свободны от напряжений;

• •    касательные напряжения на продолжении разреза в бесконечном упругом теле равны нулю вследствие очевидной нечётности их распределения относительно координаты, нормальной к плоскости, содержащей границу контакта, что соответствует исходному предположению об отсутствии сдвигового взаимодействия между рассматриваемыми телами;

• •    напряжения в концах разреза непрерывны;

• •    на «бесконечности» (вдали от площадки неконтакта) напряженное состояние в упругом теле переходит в пределе в напряжённое состояние, определяемое заданным изначально постоянным давлением p.

В качестве примера рассматривается впадина в жестком теле, которая имеет вид: Z = -Z 0 l 2/( x 2 + 1 2 ) , где Z 0 и l — параметры размерности длины, причем Z 0 <<  l • Решение этой задачи, удовлетворяющее условиям непрерывности напряжений в концах площадки неконтакта в области впадины, получено в работе [1], где распределение давления на продолжении площадки неконтакта, то есть контактное давление, p_c и полуширина площадки неконтакта a определяются по формулам:

Pc = Р

x^ x^ — a² (3l² + 2a² + x²) (x² + 1 2 ) 2

a = 1

( 2 (1 — v2) Ip J

Для исследования поведения контактного давления и полуширины площадки неконтакта в зависимости от приложенного на бесконечности давления p здесь, как и в [1], осуществляется переход к безразмерным параметрам. При этом все величины с размерностью длины относятся к l , а величины с размерностью напряжения — к р кр = E £ 0/ 2(1 - v ² )1 — критическому давлению, при достижении которого во впадине отсутствует площадка неконтакта. При таком обезразмеривании координата х переходит в x = x/l , полуширина площадки неконтакта а — в a = a/l, а контактное давление р_с — в p)_c = p c/ р_кр • Соответствующий график, построенный по формуле (1) с учетом (2), приведен на рисунке 2. Построение подобных зависимостей позволяет найти диапазон изменения контактного давления p_c , для которого из уравнений модели Гринвуда– Вильямсона [3] определяются площадь микроплощадок контакта масштаба X и безразмерное сближение контактирующих тел.

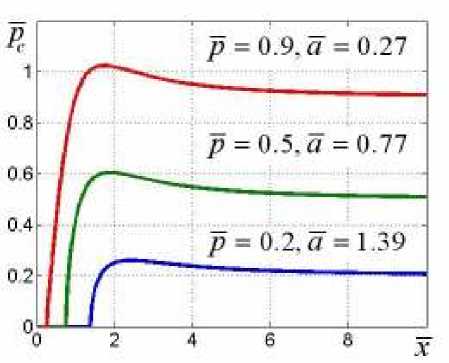
Рис. 2. Распределения контактного давления p _с на продолжении площадки неконтакта при разных уровнях давления p и при соответствующих значениях a

• 3.    Задача о распределении площади микроплощадок контакта и сближения на продолжении впадины

  • 3.1.    Основные зависимости для модели Гринвуда–Вильямсона

Шероховатость поверхности, согласно модели Гринвуда–Вильямсона [3], моделируется системой сферических сегментов одинакового радиуса в , а их высота считается случайной величиной, подчиняющейся некоторому закону распределения ф (z) . Основные зависимости для модели Гринвуда-Вильямсона таковы [3, 8]:

то

F = 4NE , p ^1/2 j ( z - Ь ) 3/2 ф (z)dz ,                                                         (3)

3_b то

A r = n N p j ( z - Ь ) ф ( z ) dz ,                                                            (4)

b где F — суммарное усилие, действующее на площадку контакта, имеющую номинальную площадь Anom ; N — число сферических сегментов на рассматриваемой площадке Anom ; Ar — фактическая площадь контакта (суммарная площадь площадок контакта). Величины F и Ar зависят от сближения b контактирующих поверхностей.

В рассматриваемой задаче вместо зависимости F от заданного сближения b используется зависимость номинального давления p = F / Anom от b . Эта зависимость монотонна и, следовательно, существует обратная ей зависимость b(p). Соответствующая безразмерная зависимость b (p )= b( p) с приведена на рисунке 3  (о — среднеквадратичное отклонение высот мелкомасштабной шероховатости, подчиняющихся гауссовому распределению [3]). Для её вычисления взяты параметры из примера, рассмотренного в работе [3] (см. стр. 305: п = N / Anom = 300 мм-2; в • о = 10 4 мм2; E,(в/о) = 25кГ/мм2; Anom = 100мм2; E* = E/(1 -v2)), а также следующие значения модуля Юнга и коэффициента Пуассона: E = 22000кГ/мм2, v = 0,3 .

• 3.2.    Решение поставленной задачи

Решается задача о протяженной впадине в жёстком теле, контактирующем с полубесконечным упругим телом (см. раздел 2).

Согласно изложенному во введении подходу, значение p отождествляется со значением pс , выражаемым формулой (1) с учётом формулы (2) при надлежащем выборе параметров в этих формулах, включая и те, которые задают впадину. В результате находятся зависимость сближения b(x) и, с учётом формулы (4), зависимость Ar(x) .

Впадина, описываемая уравнением Z = -Z01 2/(x 2 +12), имеет параметры: Z0= 1 мкм; 1 = 100 мкм, а для упругого тела используются следующие механические характеристики: E = 22000 кГ/мм2; v = 0,3. Расчеты проведены для двух значений давления, приложенного вдали от впадины (то есть на бесконечности): p1 = 0,12 кГ/мм2; p2 = 0,3 кГ/мм2. Этим значениям давления отвечают длины площадки неконтакта 2a , равные 2 мм и 1,5 мм соответственно. Полученные из решения распределения контактных давлений вблизи площадки неконтакта приведены на рисунке 4.

Из рисунка 4 видно, что при заданном давлении p, действующем вдали от впадины, в ближней к впадине области реализуется вся совокупность контактных давлений ниже p, а дальше начинается область контактных давлений, превышающих p.

Рассчитанные распределения безразмерного сближения b = b / с и фактической площади контакта (суммарной площади площадок контакта) A_r на продолжении площадки неконтакта для двух распределений контактного давления (Рис. 4) приведены на рисунках 5 и 6. Построенные зависимости отвечают двум разным уровням давления, приложенного вдали от впадины. Видно, что кривые b ( x )и A_r ( x ) ведут себя достаточно плавно (приближенно относительные изменения значений этих функций на расстояниях ~ 0,1 мм не превышают 10%) во всем рассматриваемом диапазоне изменения x (на продолжении площадки неконтакта), за исключением узких областей, непосредственно примыкающих к концу площадки неконтакта. Размер областей очень резкого изменения b ( x ) и A_r ( x ) составляет ~ 0,1÷0,2 мм.

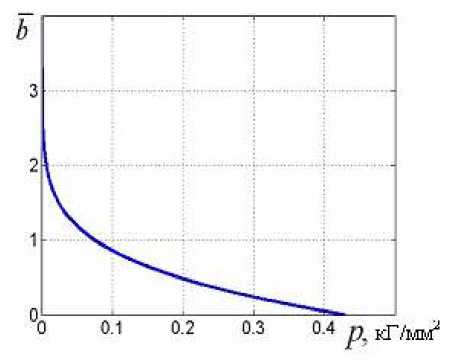
Рис. 3. Зависимость безразмерного сближения b контактирующих поверхностей от номинального давления p

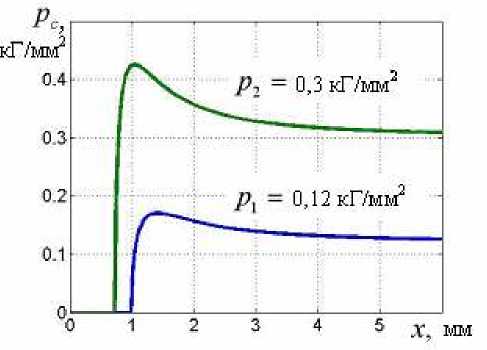
Рис. 4. Распределение контактных давлений p_c на продолжении площадки неконтакта при различных значениях номинального давления p

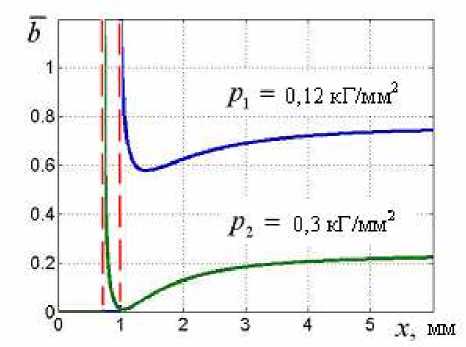
Рис. 5. Распред е ление безразмерного сближения b на продолжении площадки неконтакта

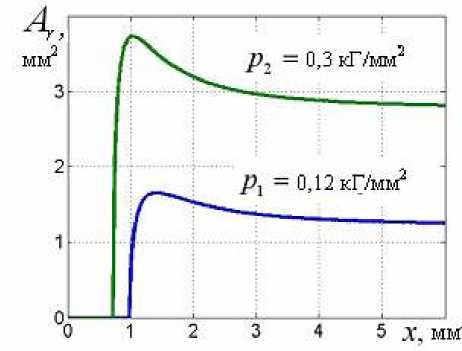
Рис. 6. Распределения фактической площади контакта A_r на продолжении площадки неконтакта

При постановке задачи принято допущение о возможности всюду пренебречь в нулевом приближении как эффектами, связанными с некоторым эквивалентным слоем, заменяющим шероховатость, так и наличием самого этого слоя. Связанная с эквивалентным слоем неоднородность напряжённо-деформированного состояния и сам слой могут проявляться лишь в достаточной близости от конца площадки неконтакта. Согласно найденному решению, контактное давление в этой области мало. Поэтому сравнительно мал здесь и эффект от проявления указанной неоднородности, что служит основанием для пренебрежения ею.

• 4.    Заключение

Значение полученного выше решения задачи состоит в следующем. В задаче имеется два макроскопически малых масштаба неоднородности Λ и λ. Масштаб Λ определяется протяженностью площадки неконтакта (связанной с характерной протяжённостью впадины). Он намного меньше протяженности микроплощадок контакта (масштаб λ). В результате создаётся относительно плавная (в меру малости λ по сравнению с Λ) неоднородность напряженно-деформированных состояний материала. Неоднородные состояния рассматриваются как локально однородные, допускающие в первом приближении использование для их описания модели Гринвуда–Вильямсона, сформулированной для строго однородных условий. В итоге появляется возможность исследовать на основе этой модели трибологические и другие явления, имеющие существенно неоднородную природу, то есть значительно расширить границы применимости модели Гринвуда–Вильямсона.

В связи с тем, что совокупность геометрий дефектов шероховатости (типа впадин) реальных поверхностей широка, в [1, 2] дана схема расчета возмущения напряженного состояния в окрестности крупномасштабных дефектов и развит подход, позволяющий рассматривать осесимметричную впадину1 и пространственные впадины более общего вида. При этом предложены способы рассмотрения впадин, геометрия которых не является гладкой, — что порождает концентрацию (в том числе бесконечную) напряжений в ближней окрестности участков неконтакта.

Полученное решение важно для ряда приложений, которые связаны с проблемами: трения и изнашивания; герметизации, когда необходимо обеспечить связность области контакта; проводимости, в частности, электрической, когда участки неконтакта экранируют протекание по нормали к ним электрического тока. Кроме того, это решение важно при рассмотрении изнашивания жёсткого тела при его контактном взаимодействии с упругим телом, когда происходит вырывание из жёсткого тела частиц с образованием соответствующих впадин (дефектов). Тогда контактное взаимодействие продолжается уже в рассмотренных выше условиях проявления локальной неоднородности напряжено-деформированного состояния, порождённой присутствием этих впадин.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 05-08-50269).