Гранулированные материалы представляют один из самых распространенных классов, состоящий как из материалов естественного происхождения (всевозможных видов грунтовых и скальных пород, включая песок, глину, илистые и лессовые грунты и другого) так и из материалов, созданных искусственно (порошковых фармацевтических препаратов, дисперсных композитов, взрывчатых веществ и подобных). Специфика гранулированных материалов проявляется в их двойственной природе: они, с одной стороны, наследуют свойства континуальной среды, а с другой, могут рассматриваться как конгломераты дискретных частиц, взаимодействующих друг с другом. В гранулированных средах при динамических процессах нагружения наблюдаются эффекты неустойчивости волновых фронтов, образование кластеров частиц, консолидация и локализация деформаций. Для представления поведения гранулированных материалов применяют как континуальные, так и дискретные модели. Континуальные модели гранулированных материалов, как правило, описываются упругими, вязкоупругими и упругопластическими уравнениями состояния, многие из которых изложены в работах [1–10].

Ниже анализируются методы и подходы, применяемые для построения континуальных моделей, используемых, в основном, при решении динамических задач механики когезионных гранулированных сред. Уделяется внимание моделям гранулированных сред, в которых удается учесть эффекты упрочнения–разупрочнения при циклических режимах нагружения. На рисунке 1 представлены основные модели, которые употребляются при решении задач динамики гранулированных сред.

Далее, в порядке общности, будут рассматриваться следующие континуальные модели:

гиперупругие ⊂ упругие ⊂ гипоупругие ⊆ упруго-пластические

В большинстве из рассматриваемых в обзоре моделей предполагается, что упругие деформации являются инфинитезимальными.

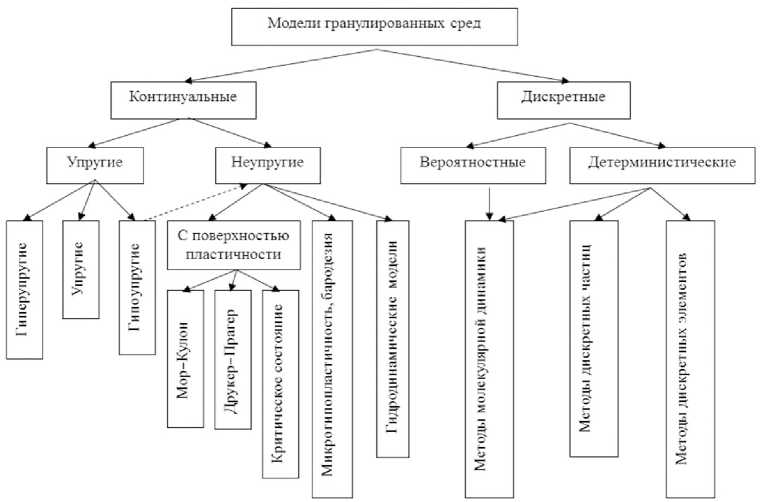
Рис. 1. Модели, применяемые при решении задач динамики гранулированных сред

• 2.    Упругие модели

• 2.1.    Гиперупругие модели

Упругие модели основаны на концепции инкрементальной обратимости соотношений между напряжениями и деформациями.

Связь между напряжениями и деформациями в гиперупругих моделях задается уравнением состояния вида

σ =λ ( I ε , II ε , III ε ) I ε I + 2 µ ( I ε , II ε , III ε ) ε ,

где коэффициенты Ламе λ и µ являются функциями инвариантов тензора деформаций:

Iε ≡tr(ε), IIε≡ 12(Iε2-ε⋅⋅ε), IIIε ≡det(ε).(3)

Уравнения (2),  (3), а также все последующие уравнения предполагаются записанными в ортонормированном базисе. Наряду с инвариантом IIε применяют также инварианты

IIε~≡ε⋅⋅ε=Iε2-2IIε,IIε≈≡Iε2-3IIε=12(3ε⋅⋅ε-Iε2).(4)

В уравнении состояния (2) I — единичный тензор второго ранга. В ряде случаев делается предположение о положительной определенности представления энергии деформирования, откуда следуют ограничения на коэффициенты Ламе

µ>0, 3λ+2µ>0 .(5)

Надо отметить, что условие положительной определенности для энергии деформирования может нарушаться в случае сред с разупрочнением.

Подстановка определяющих соотношений (2) в уравнения движения с учетом линеаризованных соотношений Коши дает уравнения Ламе в терминах перемещений:

(X + 2ц)Vхdivхu - цrotх rotх u+(VхX )divхu + Vхц ■ (Vхu + VхuT) = pu , где ввиду (2)

V х X = f#V х1s +#■ V х11г+дХ- V хШ/1.(7)

\У

Градиент V _х ц определяется аналогично. Описания и свойства дифференциальных операторов в выражениях (6), (7) можно найти в [11-13].

В дополнение к условию (2) для гиперупругого изотропного материала требуется существование скалярного потенциала ^ ( I _в , II _в , III _s ), такого, что [11]

a = V ₆ ^ ( I _Е , II г , III ₆ ).

При учете соотношений (3) условие (8) может быть записано в виде [12]:

а  'J1 +fr(Iв1 -^Ят(е^-I=Е+IIв1).

s           в                        s

Сравнение выражений (2) и (9) дает представление упругих констант в терминах гиперупругого потенциала

\( т IT TH — dV r-1 । 5V । SV tt r-1

^{X (} I s , II s,^Шs )    5 1 _s I s ⁺ 5 II _s ⁺ 5 III _s II s I s ,

^{2 ц (} I s , II s , III s ) = -|д^ + c I ^ ^{( s}   - I s ) .

Условия (10) накладывают ограничения на потенциал V . В частности, поскольку константы Ламе, в предположении их непрерывной зависимости от инвариантов, должны быть ограничены при ||s|| ^ 0 , из (10) вытекают следующие асимптотические оценки:

= O ( I s ), I s ^ 0;  d^ = O ( I s ), I ,   , 0;   gg- = о (_ш s ), _шs  , 0.              (11)

s                                                                                 s_£

Замечания 1.

• а)    Если II _s может обращаться в нуль при некотором отличном от нуля тензоре s , то инвариант II ~ , совпадая с квадратом шуровской нормы ||a|| = V a ■■ a , где черта над символом означает операцию транспонирования, уже отличен от нуля и положителен при любом ненулевом действительном тензоре s . Инвариант II” положителен при любом симметричном тензоре s , отличном от c I , где c ^ 0 — произвольное действительное число.

• б)    Уравнения движения в форме (6) одинаковы для упругих и гиперупругих изотропных сред.

• в)    Уравнения (6) показывают, что в среде с определяющими уравнениями (2) распространение продольной и поперечной волн вида

u ( x , t ) = m Х ( r ( n ■ X - ct )),

где m — векторная амплитуда, r — волновое число, n — волновая нормаль, а c — скорость распространения, вообще говоря, зависит от волновой функции х , в отличие от упругой изотропной среды с X = const, ц = const, для которой скорости инвариантны по отношению к виду волновой функции х [13]. Действительно, для динамического поля смещений (12) тензор деформаций имеет вид:

s = -^-(m ® n + n ® m).

В случае продольной волны ( m = n ) тензорные инварианты в (3) представимы как

I _е = r X , II _Е = 0, III , = 0.                                          (14)

В условиях (12)-(14) уравнения движения (6) дают следующее выражение для скорости продольной волны:

c

P

^ + 2Ц +1 ( дХ,?дц)

Р    Р1^IЕ + 2 5IJZ

Для поперечной волны ( m ■ n = 0) тензорные инварианты (3) уже другие:

IЕ= 0,  IIЕ=— r X,  iiiЕ= 0.

Из уравнений (12), (16) по аналогии с предыдущим случаем получим скорость поперечной волны:

c

2 = ^

S Р

11^ + 2^ р(дIIЕ    дIIeJ

Выражения (15), (17) показывают, что в среде с определяющими уравнениями вида (2) скорости распространения объемных волн, вообще говоря, непостоянны; кроме того, из-за присутствия в (15), (17) волновой функции X такие среды могут быть дисперсионными.

При рассмотрении задач динамики гранулированных сред весьма часто прибегали к гиперупругим моделям [14-20], причем в большинстве этих работ в основе построения решений лежала концепция разномодульности, в аналогичном контексте примененная в [21-23] с использованием упругого потенциала вида

V ( I _Е , II ; ) - a I _Е ² +e II ; +у I _Е .[лх ,

где а , в , у — упругие постоянные, не зависящие от инвариантов I _Е , II _Е , при этом инвариант II _Е определен формулой (4). Также предполагалось, что выполняются асимптотические оценки (11). Надо отметить, что в средах, определяемых потенциалом (18), в [14-19] рассматривали задачи распространения акустических нелинейных волн.

Введение параметра у в потенциал (18) позволяет учесть зависимость свойств среды от знака первого инварианта. Также с помощью экспоненциально убывающих потенциалов вида

V ( I Е , II Е ~ ) = V 1 ( I Е , II Е ~ )(1 - exp( -x ( II Е ~ )),

Х(IIЕ~) ^ 0 при IIЕ~ ^ 0 и х(IIЕ~) ^^ при IIЕ~ ^м, где V1(IЕ, IIЕ) — некоторый (невыпуклый) потенциал, можно исследовать среды с ниспадающей кривой деформирования; потенциалы такого рода введены в [14] в связи с рассмотрением «мягких» материалов с малым начальным модулем.

• 2.2.    Упругие модели

Упругие модели в случае изотропной среды при инфинитезимальных деформациях определяются законом состояния:

О = Х ( I . , II „ , III _о ) I Е I + 2 ц ( I , , II . , III . ) ■ е .                                     (20)

Предполагается, что неравенство (5), обеспечивающее положительность энергии деформирования, выполняется.

По аналогии с (6) уравнение движения в перемещениях, c учетом линеаризованных соотношений Коши, представимо в виде:

^{X +} 2 ^— V div u - ^— rot rot u + ¹ ( V X- div u + V ц- ( V u + V u ^T ) ) + b = u .             (21)

x x        xx        x     x     x x     x

'V'

слагаемые низшего порядка

Следует отметить, что наличие слагаемых, содержащих градиенты упругих модулей, существенным образом сужает круг аналитических решений: даже для безграничной среды получить фундаментальное решение уравнений (21) в замкнутом виде не удается. Однако с помощью главного символа этих уравнений — выражения

^ ® ^ + f ^— Id² -to ² 1 1 vP )

A(x, E, to) ^ 4п21 X + — Ip

может быть построен параметрикс [25]

E ( x , d , to ) = -Ц ( f l (x , d , to ) E ® £, + f 2 (x , d , to ) I ) ,                               (23)

4 n ²

где fl (x, E, to) =-Xp— ^p^|2 -to21 1 (^ E2 -to21 1,  f2(x, E, to) =(P^|2 -to21

В выражениях (22)-(24) E отвечает параметру преобразования Фурье по пространственным переменным. Далее, с помощью итерационного процесса по параметриксу (23) может быть построено фундаментальное решение для безграничной среды [25].

Несмотря на большую общность концепций упругой и гиперупругой сред, для описания динамики гранулированных сред теорию упругих сред применяют реже. В [26, 27] рассмотрены вопросы определения скоростей распространения акустических волн в системе, состоящей из упругих шаров, взаимодействие между которыми представляется решением задачи Герца. В [28, 29] для учета разномодульности среды использовались уравнения состояния, фактически приводящие к уравнениям теории упругости анизотропного тела.

• 2.3.    Гипоупругие модели

Следуя [30-32], скорость напряжений ст в гипоупругой среде определяется линейной зависимостью от скорости деформаций £ . При описании процессов, связанных с большими деформациями, значительную роль в этой зависимости играет выбор тензора скорости напряжений ст . Однако при изотермическом нагружении, в контексте инфинитезимальных деформаций, закон состояния гипоупругой изотропной сжимаемой среды упрощается и может быть записан в виде:

ст = X ( I ст , II ст , III ст ) I £ I + 2 ц ( I ст , II ст , III ст ) - £ , (25)

где

ст ^ dt

(полная производная по времени совпадает с частной в инфинитезимальном случае);

Инфинитезимальные уравнения движения, записанные в терминах скоростей напряжений, принимают вид diver + pb = pv ,

где p — плотность среды (предполагается, что p = 0); b — поле скоростей массовых сил. Подстановка уравнения состояния (25) в уравнения движения (26) с учетом линеаризованных соотношений Коши дает

Е = 2 (V хv + V х vT)

и уравнения движения в терминах скоростей

^+^ V _X div _X v - p rot _X rot _X v + V _X p div _X v + V _X p ■ ( V _X v + V _X v T ) + b = v ,             (28)

'V'

слагаемые низшего порядка где

v x =11 a^v j . dx v a +

X p p(dIa ха dIIa X a

dX d III _o

V III _a ) . X M

Градиент V _х ц определяется аналогичным образом.

Распространение объемных ударных волн в безграничной гипоупругой среде при неинфинитезимальных деформациях исследовалось в [37, 38] с помощью построения асимптотических оценок вблизи ударного фронта. При этом, в отличие от (27), здесь использовались нелинейные соотношения Коши. Случай слоистых гипоупругих сред и гармонических SH-волн рассматривался в [39], а в [40] при тех же условиях — волны Лява. Важно, что дисперсионные уравнения в [39, 40] удалось получить лишь для одного частного случая гипоупругой среды. В заключение заметим, что в случае монотонных [41] и циклических [42, 43] нагружений, приводящих к большим деформациям, применение гипоупругих моделей, а также некоторых упругопластических моделей может давать (при неверном выборе объективных производных) нефизичные осцилляции в решении.

• 2.4.    Обобщения упругих и гиперупругих моделей для учета гистерезиса

• 2.4.1.    Гистерезис при малом числе циклов

Для учета эффекта гистерезиса при циклических воздействиях рассмотренные выше упругие и гиперупругие модели нуждаются в модификации. Модификации осуществляются с использованием двух подходов.

Для описания эффекта Маллинса, проявляющегося при малоцикловом деформировании эластомеров [44], используют концепции изменения пути деформирования при разгрузке и уменьшения потерь энергии упругого деформирования при повторных нагружениях за счет исчерпания способности полимеров к размягчению [45–48].

Основная идея, реализованная в [45, 47], состоит в выборе (i) гиперупругой модели деформирования с потенциалом V и (ii) введении в потенциал V дополнительного параметра п , характеризующего как вид нагружения, так и возможное изменение самого гиперупругого потенциала при последующих нагружениях (см. также [47, 48]). Эта концепция фактически повторяет идею [35] переключения законов состояния при активном нагружении и разгрузке, предложенную для гипоупругих сред. В модели (i) гиперупругий потенциал разбивают на три составляющие [45, 48]:

V ( I _Е , II _Е , п ) = nV dev ( II _Е ) + V vol ( I _Е ) + v ( n ) .

С учетом (30) уравнение состояния приобретает вид r = ndr ( IIЕ ) - P (IЕ )I .

В (31) и далее d _a — девиатор тензора напряжений. Таким образом, здесь возможная неупругая часть соответствует только девиаторной составляющей.

Далее при этой концепции формулируют условие для определения параметра п :

П = 1-- erf r_d

max dev dev

m +в^ max

где r d >  1, m >  0, в> 0 — материальные параметры, причем в [35] параметр в считали нулевым; ¥ maX — максимальное значение потенциала; ¥ _dm — значение за все время нагружения; на начальном этапе нагружения принимали ¥ mX = ¥ _dev . Надо отметить, что при численных реализациях значение в = 0 приводило к неустойчивости вычислений, в особенности при малых значениях m ; в дальнейшем для обеспечения устойчивости счета в знаменатель функции ошибок в формуле (32) был введен параметр в^ mx .

Одним из очевидных достоинств первого подхода является возможность вариации в широких пределах параметров r d >  1, m >  0, в >  0 для «подгонки» численной модели к данным экспериментальных исследований при циклических воздействиях. Недостатки таких моделей следуют из их достоинств: параметры r d >  1, m >  0, в >  0 фактически не связаны с физической стороной процесса деформирования и механизмами диссипации энергии при циклических воздействиях, а играют роль «подгоночных» параметров.

По-видимому, подход [45–48] для моделирования динамики гранулированных сред не применяли.

• 2.4.2.    Гистерезис при большом числе циклов

Для исследования процессов, связанных с моделированием гистерезиса при большом числе циклов, может быть использована методика, предложенная в [49] и развитая в работах [50, 51]. Так же, как и при моделировании эффекта Маллинса, в подходе [49–51] неупругая часть энергии ассоциируется только с девиаторной частью. Однако если при моделировании эффекта Маллинса неупругая часть энергии была связана с уменьшением девиаторной составляющей напряжений за счет введения масштабного параметра п в формулу для потенциала (30), то в рассматриваемом — втором, подходе появление гистерезиса обусловлено (i) разбиением тензора деформаций на две составляющие

⁸ = ⁸ a + 8 в ,                                                    ⁽³³⁾

связанные с молекулярными цепочками A и B , и (ii) предположениями о гиперупругих деформациях в цепочке A и деформациях ползучести в цепочке B :

m - 1

d 8 в = A ( X Г - 1 + E ) C ( II - в ) d _a , .                                   (34)

ε = ε _e + ε _pl ,                                                       (35)

а также разложение тензоров напряжений и деформаций на шаровую и девиаторную части:

σ =- p I + d , p =- ^{I σ} , d = σ+ p I ;

^{σ 3 σ}                                               (36)

ε = θ ₃ I + d ε , θ= I ε , d ε = ε - θ ₃ I .

Связь между напряжениями и деформациями в упругой зоне задают, как правило, соотношениями линейной теории упругости. При достижении предела упругости появляются пластические деформации. Предельную поверхность пластичности описывают уравнением

• f(Iσ,IIσ,IIIσ,Iεpl,IIεpl,IIIεpl)=0,(37)

где f — выпуклая функция тензорных инвариантов.

В большинстве рассматриваемых ниже моделей функцию f предполагают не зависящей от третьих инвариантов тензора напряжений и тензора пластических деформаций:

f(Iσ,IIσ,Iεpl,IIεpl)=0.(38)

С учетом разложения (36), а также в результате введения девиаторных норм qσ≡dσ,   qεpl ≡ dεpl(39)

уравнение поверхности пластичности (38) можно записать в следующем виде:

f(p,qσ,θεpl,qεpl)=0.(40)

Поверхность пластичности описывает состояние материала. Предполагается, что при f <  0 материал работает упруго, а при f = 0 находится в зоне пластичности.

• 3.1.1.    Теории пластического течения для идеально-пластических сред

В отсутствие упрочнения или размягчения считают, что напряжения полностью обуславливаются упругой частью тензора деформации

σ = λeθeI +2µeεe,    θe=tr(εe) ,(41)

где λ _e и µ _e — упругие константы Ламе. В дополнение к уравнению состояния (41) в большинстве рассматриваемых моделей предполагают, что функция f является либо потенциалом скорости пластических деформаций (в случае ассоциированных законов течения [52])

6pi =Л7О f ,(42)

где Λ — параметр, определяющий либо инкремент пластических деформаций, либо (в случае неассоциированных законов течения) считается, что скорость пластической деформации может быть выражена через градиент ∇ _σ f с помощью линейных соотношений вида

6pi =ЛQ-Vof ,(43)

где Q ( I _ε , II _ε ) — тензор поворота (собственный ортогональный тензор), зависящий от соответствующих инвариантов тензора пластических деформаций и характеризующий отклонение 6 _pl от градиента V _o f . Угол отклонения определяется выражением

γ = arctg

∇ σ f ⋅ Q ⋅∇ σ f ∇ σ f ²

Неассоциированные законы течения также можно записывать с помощью потенциала пластического течения g ( p , q _σ , θ _ε , qI _ε ), причем по аналогии с потенциалом (40)

8pl =ЛVOg .(45)

Заметим, что в теориях пластичности параметр Л весьма часто обозначают как X .

В рассматриваемых теориях при наличии пластического течения формулируют условие согласования Гейрингер [52]

f = 0,(46)

которое указывает на принадлежность инкремента напряжений поверхности пластичности. В случае ассоциированного закона течения (46) может быть записано в виде:

Va f --a = 0.(47)

В случае ассоциированного закона течения (42) условие (47) вместе с условием Λ≠ 0 (при пластическом течении) означают, что работа приращения напряжений на приращениях пластических деформаций равна нулю:

8pi -6 = 0.(48)

При неассоциированном законе течения (45) считают, что условие (48) выполняется для потенциала (45):

Vag S = 0.(49)

Условие (48) позволяет определить неизвестный параметр Λ . Для этого уравнение состояния (41) записывают в терминах инкрементов тензоров полной и пластической деформаций (35):

a = Ce „(s -ЛVag),(50)

'V' εpl где Ce — четырехвалентный тензор упругости, отвечающий упругому изотропному материалу:

.*.

C e =λ e I ⊗ I + 2 µ e I ⊗ I .

В (51) знак ⊗ означает пермутацию индексов (перемену пары внутренних индексов в соответствующем тензорном произведении). Здесь надо отметить, что в предположении симметричности тензора малых упругих деформаций выражением (51) полностью определяется тензор упругости изотропной среды; в случае несимметрического тензора упругих деформаций (в настоящем обзоре этот случай не рассматривается) второе слагаемое в правой части (51) должно быть видоизменено (см. [11, 13]).

В уравнении (50) используют потенциал неассоциированного пластического течения (45); в случае ассоциированного закона течения с потенциалом (42) уравнение (50) очевидным образом изменяется. Уравнение состояния (50) является уравнением Прандтля–Рейсса [52].

Подстановка инкремента напряжений — правой части выражения (50), в уравнение (49) дает соотношения:

Λ= H ( f )

8 C e 'У g ∇ _σ g ⋅⋅ C _e ⋅⋅∇ _σ g ^,

H ( f ) =

0, f < 0, { 1, f = 0.

Функция Хэвисайда H ( f ) учитывает упругую работу материала при f <  0 и пластическое течение при f = 0 . В случае ассоциированного закона течения (42) градиент ∇ _σ g в уравнении (52) заменяется на ∇ _σ f .

Полученное выражение для параметра Л позволяет записать уравнение состояния (50) в виде:

* = |C e

—

H ( f )

Vag -Ce "V,g

V _c g ®V „ g C e

■■8

где выражение в скобках может рассматриваться, как некоторый (секущий) четырехвалентный тензор упругости [49, 50]:

—

H ( f )

secant e

^V d g "^C e "^Vd g

V _a g ®V _a g C e .

Так же, как и в предыдущих уравнениях, в случае ассоциированного закона течения (42) градиент V _d g в уравнениях (53), (54) заменяют на V _d f .

3.1.2. Теории пластического деформирования для сред с упрочнением

В пластической зоне условие, определяющее вид нагружения, может быть представлено следующим образом:

d■■8pi =d■■(dл\„g)>0 , 'V'

⁸ pl

где неравенство отвечает активному нагружению в зоне с упрочнением, а равенство соответствует нейтральному нагружению в случае пластического течения, или же разгрузке, осуществляемой по упругой модели (в последнем случае 8 _pl = 0). В обсуждаемых ниже моделях считается, что уравнения состояния при разгрузке соответствуют закону Гука.

Часто в теориях пластичности, в дополнение к уравнению (55), применяют постулат Друкера:

d ■■8 > 0,

где 8 — скорость полной деформации: 8 = 8 _e + 8 pl . В терминах шестимерного формализма условие (56) означает, что угол между векторами приращения напряжений и деформаций не превышает п/2.

В теориях пластичности с упрочнением и наличием поверхности пластичности так же, как в теориях без упрочнения, используют уравнения (42) или (43)-(45), с точностью до множителя Л определяющие тензор скорости пластических деформаций. В зоне упрочнения закон состояния записывают в виде линейного инкрементального уравнения упрочнения Прагера:

d = c8 pi,

где параметр c играет роль модуля упрочнения. Предполагают, что модуль упрочнения не зависит от выбранной меры пластических деформаций. Подстановка в уравнение состояния (57) вместо 8 _pl выражения (43) или (45) позволяет, по аналогии с (52), найти множитель Л из условия согласования (47):

_Л = H ( f ) ^ 8 C e „У , g c ^V d g ^C e "V g ’

f0, f <  0, H ⁽ f ) = { 1, f = 0.

В случае ассоциированной пластичности градиент V _d g заменяют на V _d f . Наконец, по аналогии с (53), с учетом (58) получают уравнение состояния упругопластической среды с упрочнением:

d =| C e

—

H(f) ^Vdg ®Vdg Ce )„. . c    Vdg ■■Ce "Vg j .

CZ^

secant

В теориях пластичности с упрочнением и поверхностью пластичности (37)-(40) обычно рассматривают два типа упрочнения: изотропное и кинематическое.

Изотропное упрочнение характеризуется равномерным (изотропным) расширением поверхности пластичности и, соответственно, расширением упругой зоны в зависимости от интегральной меры пластической деформации (см. Рис. 2 а ):

q*pi =Н1е pil dт,

где v — некоторая неубывающая функция; d т — инкремент квазивремени. Интегральная мера (60) учитывается в выражении для поверхности пластичности (40). Несмотря на очевидные ограничения, связанные с «исчерпанием» пластичности при большом числе циклов и переходом в упругое состояние, модели на основе изотропного упрочнения все же находят применение при решении задач динамики гранулированных сред.

Кинематическое упрочнение характеризуется сдвигом поверхности пластичности в зависимости от меры пластической деформации, при этом расширение упругой зоны обычно исключается (см. Рис. 2 б) . В модели с кинематическим упрочнением функцию течения f , следуя Прагеру, обычно формулируют в виде:

f ^{( о -} c ^е pi ) = °. ⁽⁶¹⁾

В (61) параметр c играет роль модуля упрочнения и предполагается не зависящим от меры пластических деформаций. Тензор c е _pl описывает сдвиг поверхности пластичности в пространстве напряжений. Этот тензор называют кинематическим, или остаточным тензором напряжений. При моделировании циклических процессов нагружения гранулированных сред модели с кинематическим упрочнением предпочтительнее моделей с изотропным упрочнением, в основном из-за возможности учета накопления пластических деформаций при большом числе циклов.

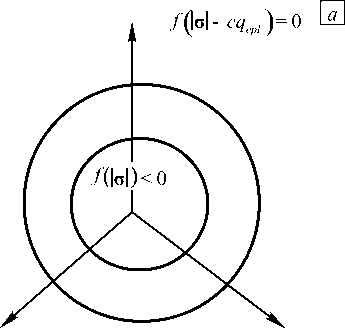
Рис. 2. Деформации поверхностей пластичности в пространстве напряжений: изотропное ( а ) и кинематическое ( б ) упрочнение

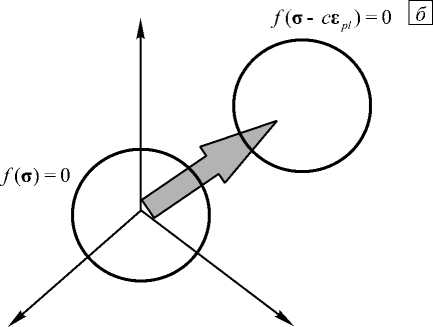
Замечания 2.

• а)    В случае, если функция f в уравнениях (37) не дифференцируема по о , скорости пластической деформации определяются на соответствующих подмножествах гладкости.

• б)    В части теорий пластичности, включая большинство теорий кэп-пластичности (в кэп-пластичности наряду с изотропным упрочнением/разупрочнением предполагается замкнутость поверхности пластического течения), постулат (56) на некоторых этапах деформирования может нарушаться, — это связано с необходимостью учета разупрочнения материала, характерного для кэп-пластичности.

• в)    При численных реализациях для подавления неустойчивости, проявляющейся при смене типа уравнений с эллиптического (для квазистатических процессов в упругой зоне) на гиперболический (в зоне пластического течения) равенство нулю в постулате Друкера (56) исключается [54, 55]. В этих случаях в (56) обычно используют строгое неравенство, заменяя уравнения идеальной пластичности уравнениями теории пластичности с (малым) упрочнением. Аналогичное условие формулируется для моделей кэп-пластичности с упрочнением и размягчением в зоне кэп-пластичности.

• г)    В теориях пластичности главные напряжения обычно не предполагаются ранжированными по убыванию; это обстоятельство принимается во внимание в дальнейшем.

• д)    В некоторых работах (см. [53]) выражение (52) для параметра Λ при неассоциированной пластичности получают из комбинации уравнений (47) и (49):

л= * Ce -У,f

.

∇ σ g ⋅⋅ C e ⋅⋅∇ σ f

Учитывая (62), в уравнениях (53) и (54) необходимо изменить знаменатели.

• е)    В моделях идеальной пластичности (без упрочнения) силовое нагружение может рассматриваться лишь при напряжениях, не превышающих предел текучести, однако при кинематическом нагружении это ограничение снимается. Модели пластичности с упрочнением могут применяться как при силовом, так и кинематическом нагружении.

• ж)    Для моделирования нелинейного упрочнения в динамике пластических сред прибегают к моделям с двумя и более поверхностями пластичности [56–60]. При этом между k -й и ( k + 1 )-й поверхностями упрочнение описывается линейной моделью Прагера (57) с когезией (модулем упрочнения) c_k , а при достижении второй поверхности — ( k + 1 ), с когезией c_{k + 1} . Предполагается, что в месте контакта поверхностей пластичности соответствующие нормали к ним совпадают и выполняется условие непрерывности пластических деформаций:

• 3.2.    Подходы на основе модели Мора–Кулона

Λ k ∇ σ f k = Λ k + 1 ∇ σ f k + 1 .                                              (63)

Условие (63) записано в предположении ассоциированных пластических деформаций. Модели с несколькими поверхностями текучести могут применяться как для изотропного, так и кинематического упрочнения. Особенно простым оказывается использование этих моделей в сочетании с моделями Мора–Кулона и Друкера–Прагера — там, где условие равенства нормалей к соответствующим поверхностям пластичности выполняется автоматически.

Подходы на основе модели Мора–Кулона ограничены рамками либо теории пластичности без упрочнения, либо теории пластичности с изотропным упрочнением, в которых в качестве девиаторной нормы (39) принимают напряжения Треска:

q σ ≡ 1 2 ( σ max

-

σ min ) ,

где σ _max и σ _min — главные напряжения.

Линейные соотношения между p и q _σ , описывающие поверхность пластичности, задают в виде:

f ( p , q _σ , ε _pl ) ≡ R ( Θ , ϕ ) q _σ - c ( ε _pl ) - p tgn ϕ= 0,

где константа c связана с переходом от упругой к пластической зоне при p = 0 , причем ее значение может сдвигаться, означая изменение когезии в зависимости от накопленных пластических деформаций, характеризуемых соответствующей нормой ε _pl ; ϕ — угол внутреннего трения; R ( Θ , ϕ ) — коэффициент, зависящий от угла внутреннего трения ϕ и угла Θ , образуемого меридиональной плоскостью и одной из осей главных напряжений (обычно σ ₁ ). Для моделей Мора–Кулона коэффициент R ( θ , ϕ ) выражается следующим образом:

sin ( Θ+π 3 ) 1

R (θ, ϕ) =            + cos(Θ+π 3) tgϕ.

3cos ϕ 3

В случае неассоциированного закона упрочнения в этих моделях вместо угла γ вводится угол ψ , называемый углом дилатации (растяжения) и характеризующий отклонение вектора ∇ _σ f от девиаторной плоскости d _σ . Обозначая нормаль к девиаторной плоскости через ν _d , получим следующее выражение для угла дилатации:

n JVd, ■ Q-va f w =arctg

.

2 i    V„ f

С учетом (65), (66) закон деформирования в пластической зоне при активном нагружении описывается уравнениями вида (57), а при разгрузке — уравнениями теории упругости (2), причем при разгрузке обычно используются уравнения линейной теории упругости.

В заключение отметим, что исследование динамических процессов в пластических средах, описываемых обсуждаемыми моделями Мора–Кулона, наталкивается на определенные ограничения. Эти модели не позволяют: (i) учитывать зависимости упругих модулей от объемной составляющей упругой деформации; (ii) исследовать эффекты диссипации энергии, связанные с образованием гистерезиса, при силовых циклических воздействиях с большим числом циклов; (iii) моделировать эффект Баушингера, образование «рэтчетинга» (ступенчатого изменения); (iv) не учитывают среднее главное напряжение в норме (64). В то же время, при кинематическом циклическом нагружении и диаграмме без упрочнения эффекты образования гистерезиса могут моделироваться и в рамках рассматриваемых моделей Мора–Кулона.

Замечания 3.

• а)    Наличие множителя 1 2 в девиаторной норме (64) создает необходимость уменьшения когезии (напряжений, отвечающих началу пластических деформаций) в два раза по сравнению с соответствующими значениями в других теориях пластичности.

• б)    Для того чтобы избежать потери гладкости, появляющейся при выборе девиаторной нормы (64), при численном анализе прибегают к сглаживанию шестиугольника, определяемого нормой (64) в девиаторной плоскости (при p = 0). При этом вместо сглаживания нормы (64) применяют сглаживающий коэффициент вида [55]:

z х                 4(1 - e_s ^! )cos ² 0 + (2 e - 1) 2                3 - sin ф

R e (⁰ , Ф ) =--------;--------------- ⁵------- /        , s ,         , ^х_Л--------.                    ⁽⁶⁸⁾

2(1 - e s ² )cos 0 + (2 e s - 1)_Л/4(1 - e s ² )cos ² 0 + 5 e s ² - 4 e s ^{6 cos ф}

В (68) сглаживающий параметр e s меняется в диапазоне 1/2 <  e s <  1, причем при e s ^ 1/2 сглаженная поверхность (65) с коэффициентом R e ( 0 , ф ) вместо R ( 0 , ф ) стремится к предельному случаю, отвечающему углу внутреннего трения ф = п/ 2, известному в девиаторной плоскости как треугольник Рэнкина.

• в)    В меридиональном направлении также делают сглаживание для того, чтобы избежать потерь гладкости, появляющихся при ф >  0 в вершине пирамиды. С этой целью потенциал (65) заменяют на гиперболический (в меридиональной плоскости) потенциал вида [53]:

g ( p , q , ,| |е Д |) ⁼ V( Re (⁰ , ф) q - ) 2 ⁺ ( ^£ c ( 0 ) tg ф ) 2 ^- P tg Ф = 0,                         ⁽⁶⁹⁾

где £ — параметр сглаживания, меняющийся в диапазоне 0 < £ <  1; при £ ^ 0 гиперболическая аппроксимация (69) стремится к исходной — (65), но со сглаживающим коэффициентом R e ( 0 , ф ) .

• г)    В качестве нормы ||s _pl || в рассматриваемой модели обычно принимают интегральную норму

I• j = i Ог^.                           (70)

0 q о

Поскольку при любых нагружениях выполняется неравенство о ■■ £ _pl >  0, то в силу этого в (70) ||е _pl 11 >  0 . д) Обобщение моделей Мора–Кулона на случай учета кэп-пластичности обсуждается в разделе, посвященном моделям Друкера–Прагера.

• е)    Несмотря на известные ограничения, подходы на основе рассмотренной здесь модели Мора–Кулона применялись для исследования задач динамики гранулированных сред, в частности, в [62] моделировалась задача зарождения и начала схода лавины (см. также [63], где рассмотрены другие классы задач динамики гранулированных сред).

• 3.3.    Подходы на основе модели Друкера–Прагера

В подходах на основе модели Друкера–Прагера так же, как и в подходах на основе модели Мора–Кулона, остаются в рамках теории пластичности без упрочнения либо с изотропным упрочнением. В этих подходах в качестве девиаторной нормы (39) принимают напряжения Мизеса:

q

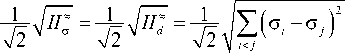
В (71) g i ( i = 1,2,3) — главные напряжения; тензорные инварианты II ” и Щ находятся по (4) с заменой тензора е на а и d соответственно.

В модели Друкера–Прагера поверхность течения определяется линейными соотношениями:

f ( Р , q а ,| I^е рА I) ⁼ q a - ^d (I^е A I) ^- P tg ^в = 0.

В (72) роль параметров d и в аналогична соответствующим параметрам в теории Мора-Кулона.

В подходах, основанных на модели Друкера–Прагера, сохраняются ограничения (i)–(iii), отмеченные при обсуждении модели Мора–Кулона; ограничение (iv) очевидным образом снимается при использовании девиаторной нормы (71).

Замечания 4.

• а)    Пластическое течение (упрочнение) изображается подобно теории Мора–Кулона либо ассоциированным законом течения с углом v = в , либо при неассоциированном законе течения с помощью формул (67), либо с помощью введения потенциала, аналогичного потенциалу (69).

• б)    В меридиональной плоскости при численных реализациях и в >  0 так же, как и в методе Мора-Кулона, осуществляется гиперболическое сглаживание вида:

g ( p , q а ,| |^е Д |) = V q а 2 +¹о^{2 -} Р tg ^{в- d} ' = 0,

где 1 ₀ = е ( d (0) - р, (0)tg в ) , P_t (0) — начальная гидростатическая прочность; d '( q _а ) — параметр упрочнения на текущем этапе нагружения; е — аппроксимационный параметр, меняющийся в диапазоне 0 <  е <  1; при е ^ 0 гиперболическая аппроксимация (73) стремится к исходной — (72).

• в)    В ряде случаев модель Друкера–Прагера дополняют кэп-пластичностью, позволяющей с помощью кэп-поверхности замкнуть конус пластичности в области больших значений давлений. В области небольших и средних значений давления поверхность течения описывается уравнением (72) или сглаженным вариантом (73), а в области больших давлений для кэп-поверхности используется следующее уравнение:

  fc ⁼ 4 ( Р - Ра ) ² +

  
  

  Rt )        ,                .

  -------------- | ^- R ( d + Р а tg ^в ) = ⁰ , 1 + а-а/ cos в J

  
  
  
  

где R — параметр формы кэп-поверхности; 0 <а< 0,05 — малый параметр, вводимый для соединения кэп-поверхности и конуса Друкера–Прагера; pa — параметр, определяющий давление при объемной пластической деформации:

pa

= Р ь ^{- Rd}

1 + R tg в ,

где p_b — предел текучести при объемной деформации. На переходном участке между конусом и кэп-поверхностью вводится вспомогательная переходная поверхность:

2 i        I а                                 ।

( Р - Ра ) +|t-I1--д|(d + Ра tg в)|

^   (   cos в J            J

-а(d + Раtgв) = 0 .

Аналогичным образом с помощью модификации уравнений (74)–(76) может быть описана кэп-пластичность для модели Мора–Кулона.

• г)    Несмотря на ограничения, присущие методу Друкера–Прагера, он используется в задачах динамики гранулированных сред для исследования динамических процессов при однократных ударах [64], а также при исследовании незнакопеременных движений гранулированной среды [65]. Модели кэп-пластичности также находят применение в механике гранулированных сред, в частности, при исследовании деформирования, учитывающего деградацию свойств материала при больших давлениях (см. следующий раздел, а также работы [66, 67]).

• 3.4.    Подходы на основе моделей критического состояния

В этих подходах модели, как правило, используют концепцию изотропного упрочнения совместно с ассоциированным законом пластического течения. Необходимость применения этих моделей диктуется появлением зон разупрочнения, наблюдаемых в большинстве гранулированных материалов при больших значениях давления.

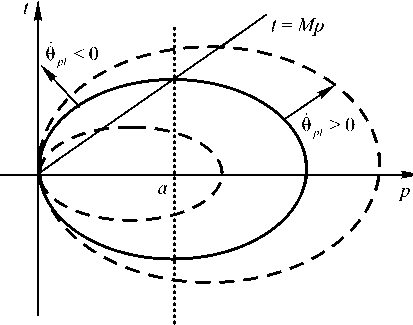
Рис. 3. Меридиональное сечение поверхности пластичности для модели критического состояния Кэм-клэй: вертикальная пунктирная линия – критическая линия, разделяющая в начальном состоянии зоны упрочнения ( ё pi >  0 ) и размягчения ( ё p <  0 )

На рисунке 3 показано сечение меридиональной плоскостью поверхности пластичности в модели Кэм-клэй (Cam-clay). Пластичность здесь представляется в виде двух соединенных между собой полуэллипсоидов: первый характеризует пластичность в области сверхкритического «сухого» состояния, когда при достижении поверхности критического конуса объемная составляющая инкремента пластических деформаций уменьшается: ёpl < 0 (причем только в моделях критического состояния ёpl = — tr(spl)), и происходит размягчение материала с одновременным уменьшением поверхности пластичности. Второй полуэллипсоид характеризует поведение материала во «влажной» области, связанной с упрочнением. В этой зоне инкремент пластической составляющей объемной деформации увеличивается: ёpl > 0 и наблюдается расширение поверхности пластичности (Рис. 3). В месте соединения эллипсоидов (критическое состояние) объемная деформация не   меняется,   и при ассоциированном законе течения девиаторных составляющих (ёpl = 0).

В

пластическое деформирование осуществляется только за счет рассматриваемых теориях поверхности пластичности в докритической и закритической зонах

описываются одним уравнением:

f ( p , q ) = - I p - 1 1 +1-^1- 1 = 0.                                 (77)

P^ a )  ^ Ma)

В (77) P — это параметр, характеризующий вид эллипсоида: для докритического состояния («сухая» зона), здесь обычно Р = 1, а в закритической зоне принимают Р <  1; параметр а равняется величине проекции на ось p радиуса-вектора точки пересечения критической линии t = Mp с начальной поверхностью пластичности; M — тангенс угла наклона критической линии к оси p ; наконец, t = q для классической Кэм-клэй модели и t = q/g , где для модифицированной модели

2 K

g = 1 + K + (1 - K)(bq)3 '

Здесь K — безразмерная материальная константа, лежащая в диапазоне 0,778 <  K <  1,0 (случай K = 1

отвечает классической Кэм-клэй модели); в (78) параметр составляет b = 3/ III_d . о

При динамических (или квазистатических) воздействиях эволюция поверхности пластичности задается с помощью кусочно-линейной аппроксимации пластической составляющей давления p_pl в зависимости от 9 pl , определяемой по экспериментальным данным, а также параметра a, вычисляемого по формуле [68]:

ppl

.

a =——

1 + в

В (79) предполагается, что в > - 1.

Замечания 5.

• а)    Фактически модели кэп-пластичности, имеющие в основе модели Друкера–Прагера, рассмотренные в предыдущем разделе, могут быть отнесены к моделям критического состояния, поскольку в области кэп-пластичности деформирование следует ассоциированному закону течения и сопровождается упрочнением: инкремент объемной пластической деформации 9 pl в этой зоне возрастает (напомним, что в моделях критического состояния 9 pl =- tr( e pl )). В «сухой» зоне происходит уменьшение инкремента объемной пластической деформации и наступает размягчение.

• б)    Несмотря на некоторые ограничения, модели критического состояния находят применение при моделировании процессов нагружения (в том числе и малоцикловых) различных гранулированных сред [68–71]. Известны обобщенные модели критического состояния, описывающие нелинейное упрочнение/разупрочнение и определяемые несколькими поверхностями пластичности, состоящими из двух и более вложенных друг в друга полуэллипсоидов с общей точкой в начале координат [72, 73].

• в)    В случае динамических нагрузок, включая циклические воздействия, модели критического состояния могут найти естественное приложение в задачах, где необходимо учитывать возможное разрушение гранул при больших значениях девиаторных составляющих, приводящих к размягчению материала [74, 75].

• 3.5.    Подходы на основе моделей с распределенными поверхностями пластичности

• 3.5.1.    Микропластичность

и без поверхностей пластичности

Рассматриваемые в этом разделе подходы основаны либо на концепции кинематического упрочнения совместно с ассоциированным законом пластического течения, либо на модели материала без упрочнения.

В качестве одномерной модели в теориях микропластичности [76, 77] обычно рассматриваются параллельно соединенные элементы Прандтля (Дженкинса). В случае бесконечного числа элементов Прандтля закон состояния может быть записан в виде:

да

nJ E(h)(s-6pl (h))dh , где E(h) — распределение жесткостей пружин. В большинстве рассматриваемых в теориях микропластичности случаев E(h) = E0 (E0 = const). Тогда уравнение состояния (80) может быть представлено в виде:

( г                  I              H ( h )

^ = E 0 |s ^-f s pl ⁽ h ) P y ⁽ h ) dh I ,    P y ⁽ h ) =    ---,

I 0               J              E0

где H_y ( h ) — распределение пределов текучести, p_y ( h ) — распределение безразмерных пределов текучести. Предполагается, что

P y ^{( h} ) ^ ⁰ ,

да

J P y ^{( h} ) ^dh = 1.

Уравнение состояния необходимо дополнить условием пластического течения

8 pl ( h ) = 0, о ( h ) <  H y ( h ), Б pl ⁽ h ) * 0, ^{a (} h ) = H y ⁽ h ).

Уравнениями (80)-(83) полностью определяется состояние материала в теориях микропластичности. Замечания 6.

• а)    Известны обобщения моделей микропластичности (без упрочнения) с одномерного случая на случай пространственных деформаций [77, 78]. В этих работах объемная деформация предполагается упругой, а девиаторные составляющие описываются уравнениями вида:

( г                 I             H Л h )

d _a = 2 G o | d _E -J p y ( h ) d ,( h ) dh I , p y ( h ) = -y    ,

pl

V 0                )             2 Go где Hy (h) — распределение размерных пределов текучести. Уравнения (84) включают уравнения пластического течения:

d _Е pl ( h ) = o,     |d _o ( h )|| <  H y ( h \

d _E p ( h ) * o,     |d „ ( h )|| = H y ( h ).

• б)    В некоторых работах по одномерной микропластичности [79, 80] с помощью дополнительных пружин, установленных параллельно пластическим элементам, учитывается упрочнение.

• в)    Модели микропластичности могут рассматриваться как модели с распределенными поверхностями течения, которые при упрочнении плавно перетекают друг в друга. В моделях без упрочнения поверхности течения должны обеспечивать непрерывность деформирования.

• г)    С помощью микропластических моделей удается описать некоторые, наблюдаемые в экспериментах, особенности деформирования при циклических процессах нагружения. В частности, с помощью исследований на одномерных моделях в [78] было показано, что (i) при циклическом деформировании гистерезисная петля не зависит от среднего напряжения; (ii) рассеяние энергии не зависит от частоты;

• (iii)    выражение для диссипации энергии за один цикл деформирования имеет вид [77, 78]:

E p, = kA ^а,                                                 (86)

где к — размерный множитель; A — амплитуда внешнего циклического воздействия; а > 0 — параметр материала. В литературе по теории колебаний выражение (86) известно как формула Давиденкова для потерь энергии в гистерезисной петле (см. [81]). Еще одной особенностью моделей микропластичности является способность точного описания формы гистерезисной петли, что делает эти модели особенно привлекательными для решения задач, связанных с исследованием динамических процессов в условиях циклических нагружений (см. Рис. 4).

• д)    Известны упрощенные модели микропластичности, в которых континуальное распределение пределов текучести заменяется дискретным. В частности, получила распространение модель «билинейного гистерезиса», которая соответствует двум параллельно соединенным элементам Прандтля с пружинами одинаковой жесткости и элементами сухого трения с различной когезией [82].

  

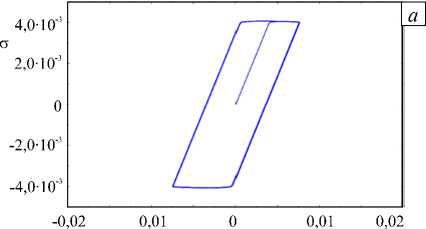
  Рис. 4. Гистерезисные петли а -8 при одноосном нагружении с гармонической кинематической нагрузкой: определяющие соотношения Треска ( а ); определяющие соотношения микропластичности для упрощенной модели «билинейного гистерезиса» ( б ); по вертикальной оси отложены значения напряжений, отнесенные к модулю упругости

  
  

  -""Л.

  
  

  4,0-10"'

  а

  2,0-10"'

  -2,0-10"'

  

  б

  02        0,01         0          0,01      0,02

  
  

• 3.5.2.    Гипопластичность

В основе моделей гипопластичности лежит концепция представления определяющих уравнений, предложенная в [81]:

О = F ( o , £ ) .

Можно показать, что для изотропного материала в случае малых скоростей деформаций уравнения (87) совпадают с уравнениями гипоупругости (25). Для этого нужно разложить правую часть (87) в ряд по £ с удержанием линейных по £ членов и учесть ограничения, накладываемые изотропией.

Уравнения гипопластичности (87) с небольшими изменениями за счет введения дополнительных переменных состояния применялись в ряде исследований, посвященных моделированию гранулированных сред при различных воздействиях [84, 85]. В частности, в [86] уравнения (87) были дополнены вспомогательными переменными состояния и представлены в виде:

⁰ = f ( f ^£ + f .| |°^| |^{2 о +} f 4I|^£||° ) , ⁽⁸⁸⁾ я1

где a — как и в подразделе 2.1, шуровская норма двухвалентного тензора a ; коэффициенты f_k ( к = 1,...,4) предполагаются функциями инвариантов тензоров о и £ и переменной состояния, определяемой коэффициентом пористости e_p :

V

.

Р _ void p_V

Надо отметить, что, как и уравнениям гипоупругости (25), уравнениям (87) присущи те же ограничения, связанные с невозможностью моделирования петель гистерезиса при циклических процессах деформирования: при отсутствии поверхности пластичности разгрузка осуществляется по тому же пути, что и нагружение.

• 3.5.3.    Бародезия

Для преодоления трудностей, связанных с отсутствием критериев активного нагружения и разгрузки, в [86, 87] предложено обобщение, которое, как утверждается в [86], хотя и не вводит в уравнения состояния (87) описание поверхности пластичности, тем не менее, позволяет в некоторых случаях нагружения учесть изменение знака нагрузки:

о = h (||о||) ( c ₂ exp( c 1 £ 0 ) + c ₃ о 0 ) ■ £ ,

где для произвольного тензора а обозначено a⁰ = a / ||а|| (здесь ||а|| , как и в подразделе 2.1, — шуровская норма); c k ( к = 1,2,3) — материальные коэффициенты, зависящие от инвариантов тензора напряжений и переменной состояния (89).

Замечания 7.

• а)    Уравнения состояния гипопластичности в форме (88) и бародезии (90) не удовлетворяют условию изотропии [13], в соответствии с которым нелинейные определяющие соотношения в зонах упругости и упрочнения (размягчения) должны иметь вид уравнений гипоупругости (25).

• б)    Несмотря на утверждение авторов [86] о возможности учета характера нагружения (активной фазы и разгрузки) в уравнениях (90), в литературе отсутствуют данные о применении уравнений состояния (90) для моделирования циклических воздействий.

• 3.6.    Гидродинамические модели

Гидродинамические модели используются для описания течения гранулированных сред в условиях, когда можно пренебречь упругой составляющей сдвиговых деформаций. Таким образом, гидродинамические модели употребимы лишь в случаях, когда пластическое течение превалирует над остальными видами деформаций.

В рассматриваемых ниже гидродинамических моделях в качестве уравнения состояния принимают уравнения движения жидкости. В наиболее общем случае эти уравнения должны учитывать возможную сжимаемость, а также сдвиговую и объемную нелинейные вязкости. Для изотропной жидкости уравнения состояния могут быть записаны в следующем виде [13]:

ст = ( - p + X ( I d , II d , III d )) I + 2 ц ( I d , II d , III d )) d ,                                  (91)

где X и ц — объемный модуль и сдвиговая вязкость соответственно; d — девиатор скоростей деформаций; p — давление.

При исследовании движений сред в условиях, близких к адиабатическим, в уравнение состояния (91) вводят дополнительную переменную состояния, связанную с температурой. Возможно введение и других переменных состояния, например пористости, по аналогии с уравнениями (88)-(90). Далее, для описания процессов пластического течения уравнение (91) дополняют уравнениями, допускающими введение термодинамического потенциала, обычно потенциала плотности свободной энергии [13]:

П = -дв^, и = -дvV ,                                     (92)

где п — плотность калории; ет — термодинамическое давление; V — плотность свободной энергии; 9 — температура; v = ||d|| — какая-либо норма девиатора скоростей. Введение потенциала (92) диктуется необходимостью определения адиабат (при исследовании быстрых процессов деформирования) или же изотерм (при медленных процессах, связанных с оттоком тепловой энергии). С помощью потенциала (92) удается учесть влияние термодинамических эффектов на механические процессы деформирования.

Замечания 8.

• а)    В исследованиях, посвященных моделированию течения гранулированных материалов, в уравнение состояния (91) вносятся упрощения. Эти упрощения связаны в основном с отказом от учета зависимости объемного модуля X от второго и третьего инвариантов, а зависимость от первого инварианта предполагается линейной. Таким образом, для моделирования течений гранулированных материалов применяют наиболее простую модель сжимаемой жидкости:

ст = ( - p + X9 ) I + 2 ц ( I d , II d , III d )) d .                                      (93)

Вводят ограничения и на зависимость вязкости ц от инвариантов девиатора скоростей деформаций. В этих работах гранулированные среды моделируют либо ньютоновой жидкостью с вязкостью, не зависящей от девиаторных инвариантов, либо применяют модели состояния (93) с вязкостью, зависящей лишь от первого и второго инварианта [88-91].

• б)    Гидродинамические модели не могут использоваться для описания эффектов, связанных с начальными этапами пластического течения и, в частности, для описания циклических процессов деформирования.

• 4. Заключение

Рассмотренные выше упругие, гипер- и гипоупругие модели находят применение при исследованиях динамических процессов в гранулированных средах, позволяя анализировать некоторые нелинейные эффекты, обусловленные разномодульностью среды, например распадом разрывов на фронте волны [18, 19]. Однако с их помощью не удается изучать образование гистерезисных петель и связанные с этим потери энергии. Исключение составляют подходы [44-50], основанные на введении в модели специфических потенциалов, учитывающих изменение знака нагрузки, но эти подходы работоспособны только при одноосных нагружениях.

Среди всего многообразия неупругих моделей, применяемых для описания деформирования гранулированных сред, модели микропластичности без упрочнения позволяют получить наиболее реалистичные результаты с точки зрения изображения динамических циклических процессов. Это, в первую очередь, связано с возможностью моделирования петель гистерезиса, максимально точно повторяющих экспериментальные данные.

В то же время следует отметить, что в рассмотренных моделях микропластичности отсутствуют механизмы учета более тонких эффектов. Назовем эти эффекты: (i) эффект Мазинга [92], наблюдаемый при деформировании некоторых полимерных материалов и состоящий в совмещении верхних ветвей гистерезисных петель, отвечающих различным амплитудам нагружений, а также в подобии кривых «прямого» и «обратного» нагружений (однако этот эффект удается учесть в специфических моделях гипоупругости, применяемых для моделирования эффекта Маллинса [44]); (ii) эффект «рэтчетинга» [93], проявляющийся в накоплении пластических деформаций при циклическом нагружении с замкнутым циклом; (iii) связанный с «рэтчетингом» специфический эффект размягчения [94], вызываемый ростом «рэтчетинга» при увеличении числа циклов; (iv) эффект упрочнения, обуславливаемый уменьшением «рэтчетинга» при увеличении числа циклов.

В заключение скажем, что перечисленные эффекты, сопровождающие циклическое деформирование металлов, в динамике гранулированных сред не играют столь важной роли [95].

Работа подготовлена при поддержке Программы фундаментальных исследований Президиума РАН № 43.