Контроль зубьев неэвольвентной шестерни цилиндроконической передачи

Введение. Цель исследования. В работе рассматривается цилиндро-коническая передача [1, 2] внутреннего зацепления (рис. 1), состоящая из эвольвентного цилиндрического колеса 2 с внутренними зубьями и конической (по форме заготовки) неэвольвентной шестерни 1, ось которой составляет угол Σ с осью колеса. На основе таких передач могут быть сформированы планетарные редукторы, альтернативные по своим кинематическим и нагрузочным характеристикам волновым передачам, но обладающие за счет отсутствия гибкого колеса значительно большим ресурсом работы [3, 4]. В цилиндро-конической передаче внутреннего зацепления можно обеспечить линейный контакт зубьев колес, если геометрию инструмента (долбяк, шевер) выполнить аналогичной геометрии колеса 2 передачи [5, 6].

Передача с малой разностью чисел зубьев (меньше десяти) имеет высокий коэффициент перекрытия, который даже для прямозубых передач может доходить до 8 и более, что обуславливает плавность работы передачи и ее высокую нагрузочную способность. При изготовлении зубьев конической шестерни возникает проблема их контроля, обусловленная сложной формой их рабочих поверхностей. Решение этой проблемы изложено в данной статье.

Уравнения боковых поверхностей зубьев. Теоретическая поверхность зубьев шестерни является огибающей поверхностью эвольвентного колеса при их относительном движении и в прямоугольной декартовой системе координат x1y1w1 (см. рис. 1), начало которой совпадает с точкой пересечения осей зубчатых колес, ось w1 – с осью шестерни, а ось y1 лежит в плоскости симмет- рии ее зуба, описывается системой уравнений [1]:

x 1 = r b2 [cosφ 1 (sinα tw – ν y2 cosα tw ) – sinφ 1 cosΣ(cosα tw + ν y2 sinα tw )] + usinφ 1 cosΣ ; (1a) y 1 = r b2 [sinφ 1 (sinα tw – ν y2 cosα tw ) + cosφ 1 cosΣ(cosα tw + ν y2 sinα tw )] – ucosφ 1 sinΣ ; (1б) w 1 = r b2 sinΣ(cosα tw + ν y2 sinα tw ) + ucosΣ ; (1в) cosα tw = cos(ν y2 + ψ y2 + φ 2 ) = r b2 /utgδ 2 ; (1г) tgδ 2 = sinΣ/(cosΣ – i 21 ); (1д) φ 1 = φ 2 /i 21 . (1е)

Здесь r b2 – радиус основной окружности колеса; φ 1 и φ 2 – углы поворота шестерни и колеса; α tw – угол зацепления; ν y2 – угол развернутости эвольвенты зуба колеса; Σ – межосевой угол; u – аппликата торцевого сечения колеса (произвольная); ψ y2 – половина угловой толщины впадины зуба колеса на основной окружности; δ 2 – угол аксоидного конуса колеса; i 21 – передаточное отношение от колеса к шестерне. Выражение (1 г) является уравнением зацепления.

Анализ этих уравнений показывает, что зуб шестерни имеет сложную бочкообразную форму, вследствие чего известные формулы для расчета контрольных размеров, применяемые для эволь-вентных цилиндрических и конических колес, не могут быть использованы для рассматриваемой шестерни.

Учитывая переменность толщины зуба по торцевым сечениям шестерни и необходимость при изготовлении определения контрольного размера в разных торцевых сечениях, наиболее удобным способом контроля является измерение размера по шарикам.

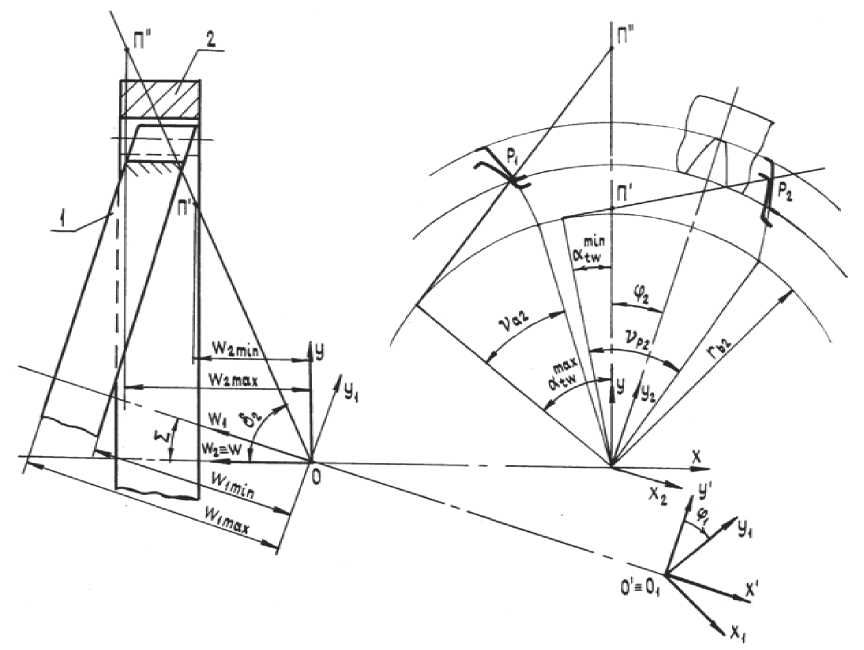
Рис. 1. Схема зацепления

Для определения размера по шарикам необходимо, зафиксировав шарик относительно торцевого сечения шестерни, ввести его во впадину зубьев до касания с их поверхностью.

Положение торцевого сечения, в котором шарик к о снется поверхности зубьев шестерни, может быть определено при решении задачи о касании сферической поверхн о сти и пов е рхности зуба шестерни, но из-за сложности уравнений поверхности зуба (см. формулы (1)), ре ш ение задачи в общем виде является проблематичным.

Метод решения. Полученные результаты. Предлагается следующий способ ре ш ения задачи.

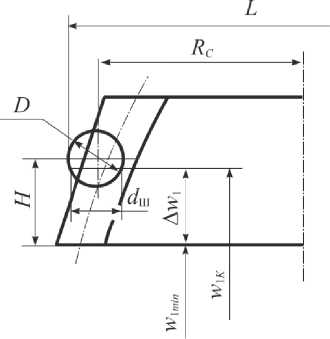
Зафиксируем шарик диаметра D относительно большего торца шестерни (рис. 2) на расстоянии H и рассмотрим торцевое сечение зуба шестерни с аппликатой w 1 = w 1K (Δw 1 – отно с ительно большего торца), в котором шарик касается поверхности зуба шестерни (положение этого сечения заранее неизвестно).

Диаметр сечения шарика равен dш = 7D2 - 4(H -Awi)2 .                                                          (2)

Уравнение профиля зуба шестерни в рассматриваемом сечении получае м следующим образом. Приняв в уравнении (1в) w 1 = const, решим его относительно v y2 , полученное выражение подставим в формулы (1а) и (1б). После преобразований уравнения профиля зуба примут вид:

x i = ^rb2 ( P ' sin Ф 1 ^- q ' cos Ф 1 ) ; (3а)

y i = r b2 ( p ' cos Ф 1 + q ' sin Ф 1 ) ; (3б) p ' = a cos 2- bsec 2 sec a tw ; (3в) q ' = ( 1 - acos a _tw + b ) cosec a _tw; (3г) a = w₁/r_b2sin 2 ; (3д)

b = ctg 2- ctg 5 ₂.

(3е)

Координаты центра сечения шарика при известных координатах его точ к и касания M c профилем зуба шестерни x 1M и y 1M (рис. 3):

x _c = x_1M + 0,5d_Ш cos ( a M - 90 ° ) ;

Ус = У1М + 0,5dш sin (aM - 90°),(4)

где α М – угол наклона касательной к профилю зуба шестерни в точке M.

Угол α можно определить по формуле tga = dy1 / dx1.(5)

Дифференцируя выражения (3а) и (3б) по α tw , после преобразований получим

e(g cos 9j - fsin 9j) + nsin ф! -1 cos ф!^

e ( fcos ф + gsin ф 1 ) - ncos Ф 1 - Isin Ф 1

Здесь:

e = [a cosα tw – (1 – tg²α tw ) – cosα tw ] / i 21 ;

f = ( acos S cos a tw - bsec S ) sin a tw ;

g = ( 1 + b - acos a tw ) cos a tw ;

l = bsec S tg a tw sin³ a tw ;

n = 0,5 [ a - ( 1 + b ) cos a tw ] cos 2 a tw .

Рис. 2. Определение размера по шарикам при контроле зубьев неэволь-вентной конической шестерни

Координаты точки касания сечения шарика и профиля зуба x 1M , y 1M определим и з условия, что когда окружность, помещенная во впадину зуб ь ев, касается обоих профилей зубьев, то ее центр находится на оси симметрии впадины, котора я в принятой системе координат x ₁ y₁ (рис. 3) расположена под углом π/z 1 к оси y 1 и описывается у р авнением:

^x1 ^- ^tg (^{n /z}1 ) = 0.                                                                             (7)

При практических расчетах радиус центра сечения шарика находится следующим образом. Решая совместно уравнения (3), (4), (6), (7) системы, найдем α tw , затем по ф ормуле (3) – координаты x 1M и y 1M , а по (6) – угол α М , после чего п о выражению (4) координаты центра сечения шарика x С , y С , по которым вычислим радиус центра окружности R С = ОС.

Апплика т у сечения шестерни w_1K, в кото р ой шарик касается поверхности зуба шестерни, установим, последовательно р а ссматривая торцевые сечения зуба шестерни в пределах высоты шарика. В каждом из сечений окружность, по л учаемую в сечении шарика, вве д ем в касание с профилем зубьев, сместив ее в радиальном (для шестерни) направлении и определим путем, описанным выше, радиу с центра окружности. В торцевом сечении шестерни, где шарик касается поверхности зуба шестерни, этот радиус окажется максимальным. Этот радиус и будет являтьс я радиусом центра шарика R C при определении размера по шарикам.

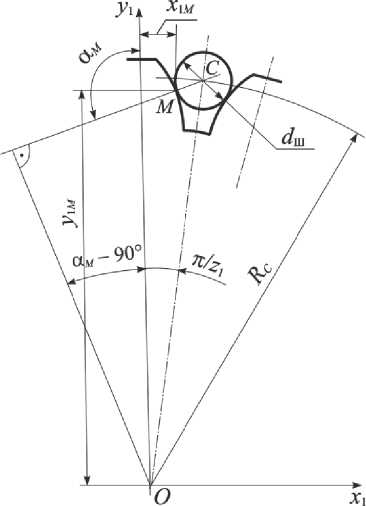
Рис. 3. К определению координат центра сечения шарика и его точки касания с профилем контролируемого зуба

Таким образом, для определения положения центра шарика необходимо найти максимальное значение функции R _Cmax = f ( w 1 ) .

Расчеты показывают, что искомое сечение смещено от диаметрального сечения шарика в сторону большего торца шестерни, поэтому можно рекомендовать начина т ь поиск аппликаты искомого сечения с торцевого сечения шестерни, проходящего через центр шарика, затем постепенно уменьшать ее до тех пор, пока радиус центра сечения шарика, достигнув макси м ума, не начнет уменьшаться. Определив радиус центра шарика, размер по шарикам L (см. рис. 2) найдем по известным формулам [8]:

при четном числе зубьев шестерни

L — 2R c + D;

при нечетном числе зубьев

L — 2R c cos-- + D .

z1

Практическая реализация работы. На рис. 4 показана схема измерения размера п о шарикам неэвольвентной шестерни, а на рис. 5 представлено приспособление дл я измерения размера по шарикам на станке при нарезании зубьев. Приспособление позволяет измерять разме р по шарикам в разных торцевых сечениях шестерни.

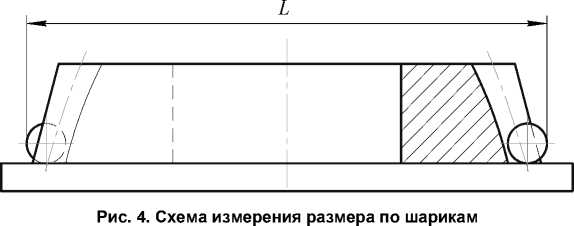
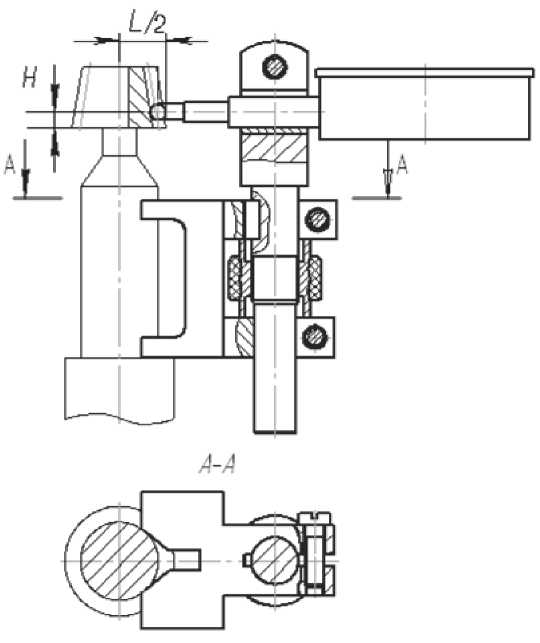
Рис. 5. Приспособление для измерения размера по шарикам неэвольвентной конической шестерни

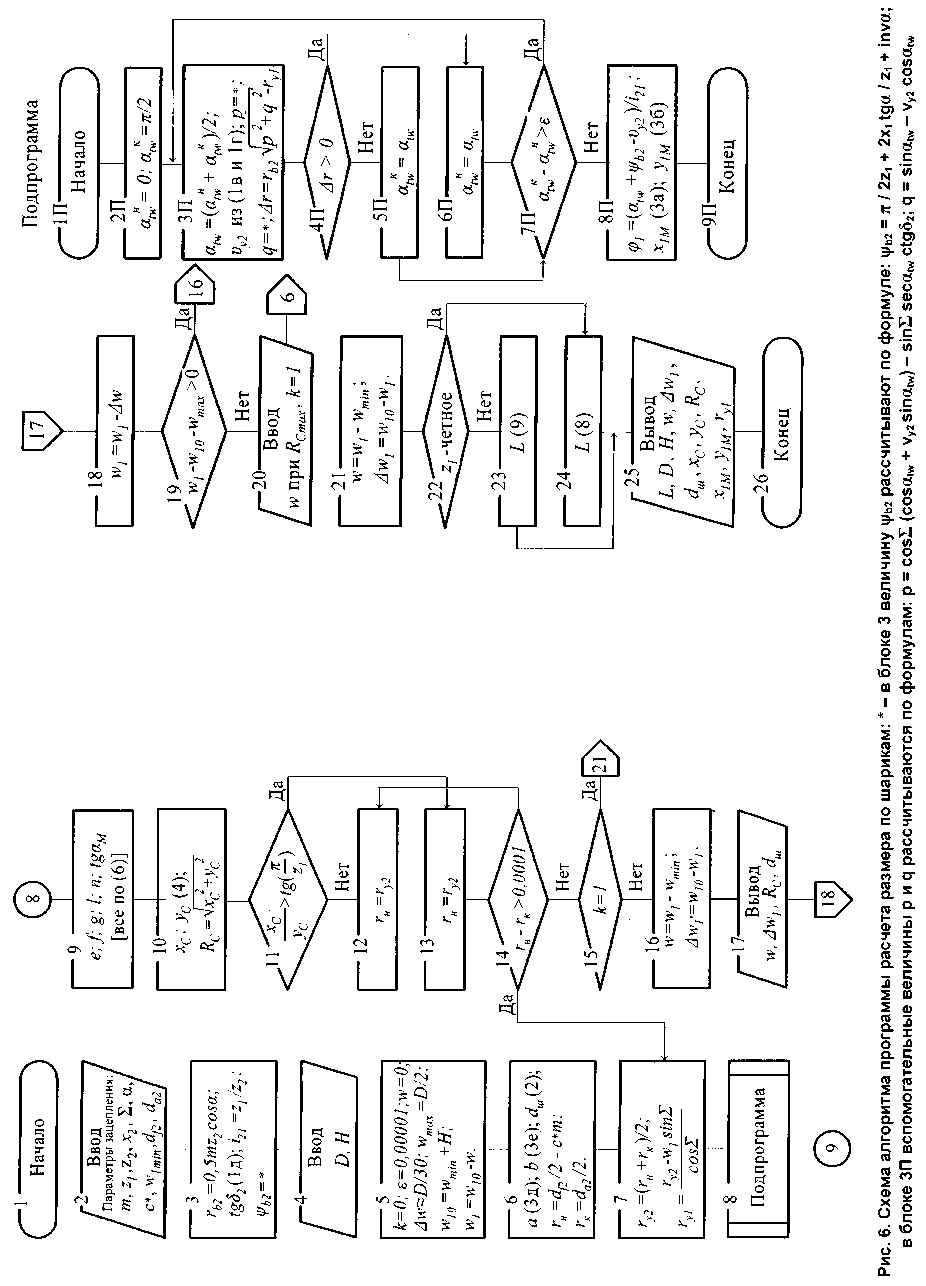
Так как определение размера по шарикам связано с большим объемом расчетов и решением трансцендентных уравнений, расчеты выполняются численными методами с применением ЭВМ по разработанной авторами программе. Схема алгоритма программы представлена на рис. 6.

В качестве примера для шестерни при m = 5 мм, z 2 = 76, x 2 = 1,74, z 1 = 68, Σ = 7°, D = 9 мм и H = D/2 получено x 1M = 4,19 мм, y 1M = 177,44 мм, R C = 179,49 мм, L = 367,98 мм. Сечение, в котором шарик касается поверхности зубьев, расположено на расстоянии 0,17 мм от центра шарика.

Заключение. Предложенный в работе алгоритм расчетов размеров по шарикам позволяет определять контрольные размеры при нарезании зубьев с неэвольвентным профилем их рабочих поверхностей в любом торцовом сечении шестерни. На практике контроль зубьев можно осуществлять с помощью простейших приспособлений, используемых для контроля зубьев с эволь-вентным профилем.