Конус устойчивости для линейного матричного дифференциального уравнения с запаздыванием
Бесплатный доступ
Построена некоторая поверхность в трехмерном пространстве, называемая конусом устойчивости. Доказано необходимое и достаточное условие асимптотической устойчивости матричного уравнения x(t) + Ax(t) + Bx(t - τ) = 0 для матриц произвольного порядка, которое связано с тем, находятся ли вспомогательные точки, зависящие только от собственных чисел матриц А и В и величины запаздывания, внутри конуса устойчивости. От матриц А, В требуется совместная триангулируемость.
Дифференциальные уравнения с запаздыванием, асимптотическая устойчивость, конус устойчивости
Короткий адрес: https://sciup.org/147158645
IDR: 147158645
Текст научной статьи Конус устойчивости для линейного матричного дифференциального уравнения с запаздыванием
Рассматривается задача об асимптотической устойчивости уравнения
x(t) + Ax(f) + Bx(t-т) = О, />0 (1)
с коммутирующими матрицами А и В и запаздыванием г > 0.
Это уравнение моделирует динамику нейронных сетей Хопфилда [1]. Матрица А описывает собственную реакцию нейрона на внешнее воздействие, а матрица В характеризует реакцию нейрона, связанную с его взаимодействием с соседними нейронами.
В [1-7] получены некоторые достаточные условия устойчивости уравнения (1). В самой ранней публикации 3. Рехлицкого [8] (1956 г.) указаны овалы устойчивости для (1) при А = 0, в одной из последних публикаций [9] (2009 г.) исследуется задача устойчивости (1) с 2x2 матрицами А, В специального вида.
Мы требуем одновременной приводимости матриц А и В к треугольному виду. Как известно [10], это возможно для коммутирующих А и В.
Уравнение (1) считаем устойчивым, если его нулевое решение является устойчивым. Рассмотрим вначале скалярный аналог уравнения (1), в котором т = 1:
х(/) + ax(f) + bx(t -1) = 0. (2)
Пусть в (2) а - действительное, b - комплексное число. Следующий результат известен (см., например, [3]).
Теорема 1. Уравнение (2) асимптотически устойчиво тогда и только тогда, когда а > -1 и на плоскости (uvu2) точка (Re b, Im 6) находится внутри овала страницей:
Mj = -acosw + wsinw,
-W] < W < W], где W] есть наименьший положительный корень уравнения а = -w/ tg w.
Если
а
> -1 и точка
(Reb,
ImZ>) находится на границе овала (3), то уравнение (2) устойчиво (не асимптотически).
На основе теоремы 1 мы даем критерий устойчивости для матричного уравнения (1), в котором матрицы
А
и
В
приводятся к треугольному виду одним преобразованием.
Определение 1.
Конусом устойчивости для уравнения (2) назовем поверхность в трехмерном пространстве
(иъи2,и3),
сечение которой на уровне
и3 = а
есть овал устойчивости (3).
Теорема 2.
Пусть
А, В, S
е
Жтхт
и
S~XAS = АТ
и
S~XBS = Вт,
где
Ат
и
Вт
- нижние треугольные матрицы с элементами соответственно
Xjs, ц^,
1 <
j,s
Построим систему точек
Mj = (и^,и2рИ3Д
1 <
j <т;
Математика uXj = гI ^ I cos(arg^ + тЬпЯр, u^j" т\^\ sin(arg Hjj + r Im ^ X (4)
ы3у- = r Re
Ху.
Уравнение (1) асимптотически устойчиво тогда и только тогда, когда все точки
Mj,
1 <
j <т
находятся внутри конуса устойчивости.
Если хотя бы одна точка
Mj
лежит вне конуса устойчивости, то уравнение (1) неустойчиво.
Доказательство.
Умножим (1) на У-1 слева. Изменим масштаб времени, положив
t-вт.
Сделаем замену
х^ = Sy(0)
. Получим
у(0) + тЛту(0) + тВту(0-Х) = О.(5)
Возвратим имя
t
переменной
0,
положим
у = (уъ...ут)т
и выпишем (5) как треугольную систему скалярных уравнений 1 <
j <т\
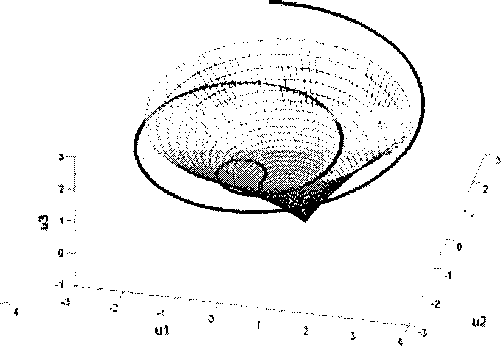
У]+Т^У}+Т^У1(1~^ = ~Т^ + ^кУк^"У)-(6) k В (6) сделаем замену yj = exp(-/Im2y/)z • и умножим (6) на ехр^ТтЯу). Получим треугольную систему с действительными коэффициентами при zy(l < j <т)\ Zj + rReAJJzJ + TjLijj expOTImA^z// -1) = ^ vjkzk + Gjkzk{t -1),(7) k Наряду с (7) рассмотрим диагональную систему Zj + г Re AjjZj + T^jj ex^iz Im Ajj )z. (/ — 1) = 0.(8) Пусть все точки Mj = (и^,и^,и^)Д < j щ = - и3 cos w + w sin w, ы2 = U3j sin w + wcos w, -wx Ввиду этого, как хорошо известно (см. [3], [5, Appendix В]), система уравнений (8) асимптотически устойчива. Перейдем к системе (7). Первое из уравнений (7) совпадает с первым уравнением системы (8), и, следовательно, асимптотически устойчиво, а поэтому все его решения экспоненциально убывают. Во всех остальных уравнениях системы (7) мы последовательно видим асимптотически устойчивые левые части и экспоненциально убывающие правые части. Поэтому все их решения экспоненциально убывают [И]. Получаем, что система (7), а, следовательно, и (1) асимптотически устойчивы. Пусть точка Mj =(uXj,u2j,u3j), определенная равенством (4), лежит на поверхности конуса устойчивости или вне его. Не теряя общности, можем считать, что j = 1. В сечении конуса плоскостью и3 =u3j ей получим овал (3). Если точка М„х = («11,м21) лежит на границе овала, то первое уравнение системы (7) не является асимптотически устойчивым, поскольку его характеристическое уравнение в этом случае имеет чисто мнимые корни. Если М*х лежит вне овала, то уравнение (7) при j = 1 вообще неустойчиво (см. [3], [5, Appendix В]). Но система (7) (асимптотически) устойчива тогда и только тогда, когда (асимптотически) устойчива система (1). Теорема 2 доказана. Рассмотрим примеры применения теоремы. Пример 1. Положим в (1) Хохлова Т.Н. Конус устойчивости для линейного матричного дифференциального уравнения с запаздыванием f 0,9 6,5) ( 1,39 0,65) А = В = . (10) (-4,8 0,9/ (-0,48 1,39) Поскольку В = 0,Ы +1,3/, матрицы А, В коммутируют и, следовательно, могут быть совместно приведены к диагональной форме [10]. Собственные числа матриц А, В суть соответственно: ^22=0,900015,5857/, ^и 22 =1,390010,5586/. (И) Вследствие симметрии изучим расположение конической винтовой линии Mj = (uXj,u2j,и3^) относительно конуса устойчивости только при j = 1 (см. рис. 1). Рис. 1. Конус устойчивости и кривая (4), (11) в двух проекциях Кривая (4), (7) дважды выходит из конуса устойчивости при значениях т, равных тх « 0,2715, т3 * 1,1965 и входит в конус при значении т , равном т2 » 0,8392. Поэтому уравнение (1) с матрицами (10) асимптотически устойчиво тогда и только тогда, когда Т е^тДи^Аз)- Пример 2. Пусть дано уравнение x(t) + Ax(t) + ВхД - г) = 0, где '-0,1 -0,01 0,03 2' -0,03 0,1 0,5 -0,3 А = ,(12) -1 5 0,04-2 ч-0,3 0,02 -0,1 0,01, В = 0,35 - ОДА + 1,5Л2. Требуется определить, при каких значениях т это уравнение устойчиво, а при каких неустойчиво. Очевидно, матрицы А, В коммутируют. Собственные числа матриц А, В имеют вид: ^=-1,4943, щ =3,7989, Л2,3 =-0,0988 ± 0,7539/, ц23 =-0,5280 + 0,2990/, (13) Л4 =1,7420, ^4= 4,6777. Построим точки Mj = (^iXj,u2j,u3j\ 1 Математика Для устойчивости необходимо и достаточно, чтобы все точки Mj = (uXj,u2j,u3j), 1< j<4 находились внутри конуса устойчивости. Две системы точек, соответствующие комплексным собственным значениям матрицы А, с изменением т образуют винтовые линии, выходящие из конуса при г = 0 и лежащие за его пределами при всех т > 0. Рис. 2. Конус устойчивости и кривые (4), (13) Две другие системы точек, соответствующие действительным собственным значениям матрицы А, образуют прямые, каждая из которых один раз пересекает конус устойчивости, а затем находится вне его. Согласно теореме 2 для асимптотической устойчивости требуется, чтобы внутри конуса находились все точки Mj =(uXj,u2j,u3j), 1< j 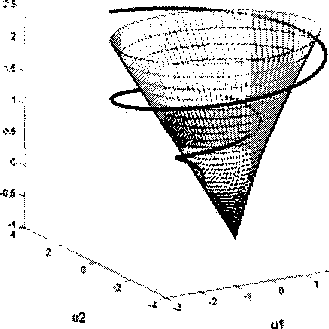

Список литературы Конус устойчивости для линейного матричного дифференциального уравнения с запаздыванием
- Gu, К. Stability of time-delay systems/К. Gu, V. Kharitonov, J.Chen. -Springer, 2003. -376 c.
- Idels, L. Stability criteria for a nonlinear nonautonomous system with delays/L. Idels, M. Kipnis//Applied Mathematical Modelling. -2009. -V. 33. -Issue 5. -P. 2293-2297.
- Кирьянен, А.И. Устойчивость систем с последействием и их приложения/А.И. Кирьянен. -Изд-во СПбУ. -1994. -235 с.
- Кирьянен, А.И. Устойчивость уравнения x(t) = ax(t-h) + βx(t) с комплексными коэффициентами/А.И. Кирьянен, К.В. Галунова//Уравнения в частных производных, ЛГПИ им. А.И. Герцена, 1989. -С. 65-72.
- Mori, Т. Simple stability criteria for single and composite linear systems with time delay/T. Mori, N. Fukuma, M. Kuwahara//Int. J. Control. -1981. -V. 34. -P. 1175-1184.
- Mori T. Stability of x{t) = Ax(t) + Bx(t-τ)/T. Mori, H. Kokame//IEEE Trans. Autom. Control, 1989. -V. 34, № 4. -P. 460-462.
- Shuenn-Shyang Wang Further results on stability of x(t) = Ax(t) + Bx(t -r)//Systems&Control Letters. -1992. -V. 19. -Issue 2. -P. 165-168.
- Рехлицкий, З.И. Об устойчивости решений некоторых линейных дифференциальных уравнений в банаховом пространстве//Изв. АН СССР. -1956. -Т. 111. -С. 29-32.
- Matsunaga, H. Stability Regions for Linear Delay Differential Equations with Four Parameters/H. Matsunaga//International Journal of Qualitative Theory of Differential Equations and Applications, 2009. -V. 3, № 1-2. -P. 99-107.
- Horn, R. Matrix Theory/R. Horn, С Johnson//Cambridge Univ. Press. -1986. -561 с
- Азбелев, Н.В. Устойчивость уравнений с запаздывающим аргументом/Н.В. Азбелев, П.М. Симонов//Изв. вузов. Математика. -1997. -№ 6. -С. 3-16.


