Конусы в тензорных произведениях упорядоченных банаховых пространств

Е^. Нормы не и кв на Е®Х, где X — произвольное банахово пространство, связанные с порядком в Е, определяются по формулам:

Для

ВСЯКОГО Z = Д к = 1

бк ® Хк Е Е ® X положим

ПеД) = inf

{|Ы1 : и >

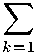
^\хк,хД,

Vx* Е АД

МК1 ,

для любого z Е Е ® X положим кв Д') = inf

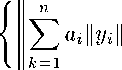
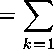
°' > О,

г < г < т

I

Эти нормы были определены в [4] и являются аналогами нормы В. Л. Левина [5], введенной им для случая, когда УБП Е — банахова решетка.

(с) 1999 Худалов В. Т.

Нормы п е и кв являются кросснормами [6] тогда и только тогда, когда норма на Е регулярна [4], т. е.

• 1)    Мх,у G Е из ±ж < у следует ||ж|| < ||у||;

• 2)    Mx Е Е и Vs > 0 Зу > 0, такой что ±ж Дуй ||у|| < (1 + е)||ж||. Если Е — УБП с замкнутым конусом и регулярной нормой, то пишем Е Е (F). Пространство Е ® X, наделенное нормой а, обозначаем Е ®_а X, а его пополнение Е®_аХ.

Данная работа состоит из двух частей. В первой части изучаются свойства тензорных конусов в произведении Е®Е, где Е и F — УБП, такие как нормальность, не-сплющенность, оштукатуриваемость, телесность, правильность, полная правильность. Показано, что всякий тензорный конус в Е ®_ПЕ F , ^гЛ^е ^ ^ (^-), ^ — УБП, является нормальным тогда и только тогда, когда конус в F нормальный. В то же время всякий тензорный конус в Е ®k_E F является несплющенным тогда и только тогда, когда конус в F несплющенный. Таким образом каждая из норм не и кв отвечает за наличие только одного из таких взаимно противоположных и взаимно дополняющих свойств, как нормальность и несплющенность произвольного тензорного конуса.

Во второй части изучаются тензорные произведения I- и Ьо-операторов [7]. Оказывается, что при подходящем выборе тензорного конуса в Е ® F, где E,F Е (F), тензорное произведение

S ® Т : Е ®а F -д X ®р Y, аир — произвольные кросснормы, двух операторов S : Е —> X иТ:F —>Y является Z-оператором тогда и только тогда, когда S и Т /-операторы.

Аналогично, тензорное произведение

U ® V : X ®aY д E^F

(а и /3 — произвольные кросснормы) двух операторов U : X —> Е и V : У Д F является Ьо-оператором, если и только если U и V — Ьо-операторы. При этом получены двусторонние оценки норм этих операторов.

• 1° . Пусть Е — УБП с замкнутым, нормальным, воспроизводящим конусом Е₊, F — произвольное УБП с замкнутым конусом.

Теорема 1. Следующие утверждения эквивалентны:

• 1)    произвольный тензорный конус К_а нормален в Е ®_ПЕ F;

• 2)    существует тензорный конус К_а такой, что К_а является нормальным в Е®_Пе F;

• 3)    конус F₊ нормальный в F.

Доказательство. Ясно, что из 1) следует 2). Докажем, что 2) влечет 3). Пусть К_а — нормальный тензорный конус в Е ®_ПЕ F, тогда норма пв полумонотонна на конусе К_р [1], так как К_р С К_а. Возьмем е Е Е₊, ||е|| = 1. Рассмотрим вложение j : F —» Е ® F, определяемой по формуле:

j^ =e®xEE®F, 4xEF.

Тогда F является подпространством в Е ®_ПЕ F с конусом К_р, и порядок в F индуцируется из Е 0 F, значит F₊ — нормальный.

3)=>2). Так как F+ — нормальный конус, то клин Fp — несплющенный. Покажем, что конус Ki — нормальный, тогда каждый тензорный конус Ка С Ki также будет нормальным. Пусть

^1

G Ki, и ^i - z₂ G Ki.

=1

г=1

Для каждого

G FT имеем:

• a)    E еДж^жД GF₊;

fc=l m

• б)    E «ДуджД G F₊;

2=1 n             m

в

Так как F^. — несплющенный клин, то

Mx* G F*,   ||ж*|| < 1 >

Уж* G F;,    ||ж*|| < 1 > .

С другой стороны, найдется константа С, не зависящая от zi и z₂. такая, что

^eV^ = С inf < ||п|| : и ^ ^^ di^Ui, х*^, Mx* Е F^_,   ||ж* || ^ 1 > .

I               г = 1

пе^ ⁼ iⁿf

Хк,х*\

= inf

xk,x*V

Тогда из в) следует, что n_e(^i) >  kriE^?)), ^гД^е константа к не зависит от zi и г₂, откуда следует нормальность конуса Ki, а значит, и произвольного тензорного конуса К_а.

ЗАМЕЧАНИЕ. Если предположить, что E,F G (F), то нетрудно видеть, что из ^1 ± г₂ G К_а, где ^i, z₂ Е Е 0 F, будет следовать, что n_e(zi) ^ п^ДД.

Приведем пример, показывающий, что из несплющенности конуса F₊ в F не следует, вообще говоря, несплющенность конуса Ki в E®_nEF (а следовательно, не следует несплющенность произвольного тензорного конуса К_а\

Пример 1. Пусть Е = Z₂ с конусом

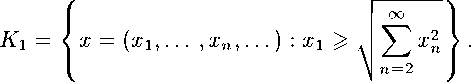
Можно показать, что Е Е (F), конус К^ — телесный и оштукатуриваемый и К^ = К. Положим F = Zi с естественным порядком. Так как Zi — банахова решетка, то конус F₊ — несплющенный.

Рассмотрим тензорное произведение Е ®ПЕ F. Тогда, так как в силу телесности конуса Ку норма пе эквивалентна норме е [4], пространство Е®ПеЕ изоморфно вкладывается в пространство C^E*,F^ с операторной нормой. Рассмотрим элементы zn Е Е ® F, zn = £ ек- ® Хк, где еД^/Д?^ = xv, ^ik — символ Кронекера, элементы zn определяют операторы Т„ : Е* —» F, действующие по формуле:

Тогда

Тп (® 1, • • • , О'

,    /    «2       П,\

• = «1,—,... , —,0,... .

\     2        п/

Так как операторы Т„ сходятся по операторной норме к оператору Т : Е* —» F , где Т определяется формулой:

гр (                               (    ^2       Ou Q:n_|_|\

• 1    ад,... ,an,an+i,... = «1, —,... , —, ——,...,

у 2 n n + 1/ то Т можно рассматривать как элемент E®nEF.

Но оператор Т нельзя представить в виде разности положительных операторов (G £^Е,Е^ [8], а следовательно, и в виде разности положительных (в смысле конуса К^ элементов из Е®_ПеЕ. Значит, замыкание К, в пополнении Е®_ПеЕ не является воспроизводящим конусом, следовательно, К; не является несплющенным конусом в Е ®_ПЕ F [1].

Теорема 2. Следующие утверждения эквивалентны:

• 1)    произвольный тензорный конус К_а является несплющенным в Е ®k_E Р",

• 2)    существует тензорный конус К_а такой, что К_а является несплющенным в Е®к_Е F;

• 3)    конус Е₊ несплющен в F.

ДОКАЗАТЕЛЬСТВО. Очевидно, что 1)=>2). Докажем импликацию 2)=>3). Пусть конус К_а несплющен в E®k_B Е. Тогда инъективный конус К; также будет несплющен в Е ®_kE F. Возьмем элемент е Е Е^, ||е|| = 1 и рассмотрим вложение ; : F ^ Е ® F, ₃^ = _е ® _х для х Е F. Пусть f G ^ такой, что /(е) = 1.

Определим проектор Р : Е 0 F -Д j(F) по формуле

Р ^е^®^ = е®^/(еД^ G ;(F).

\fc=i         )        fc=i

Так как этот проектор является положительным, то несплющенность ^Е®к_в F) наследуется подпространством j(F), значит, конус в F — несплющенный.

3)=>1): Покажем, что конус Кр несплющен, отсюда будет следовать несплющен ность любого тензорного конуса Ка. Пусть z = £ ek ® Xk — произвольный элемент

m из E®F. Возьмем е > 0. Тогда существует представление г = £ аг ® щ элемента г г = 1

m ЕаДуД г = 1

такое, что а^ > 0 для 1 < г < m и

— кв^ ^ е. Так как F+ — несплющен ный конус, то каждый элемент гр, 1 < г < т, можно представить в виде гр = у^ — уг2, где yL у^ G F+ и Цу,11| + ||уг21| < С\\уг\\, С — константа несплющенности конуса F^_ [1].

т        т            т       т

Рассмотрим элементы £ щ ® yj и £ а^ ® у². Тогда £ а{ ® yj, £ а^ ® у² G К_р и г=1            г=1                  г=1          г=1

m       m z = 52 ai ® Ui - 52 а» ® У^ • Имеем:

г=1           г=1

кв

( m

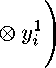
+ kE

( m

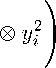
< 2C

m

52 «illy»II г = 1

< 2№(г) + 2C-e,

то есть K_p — несплющенный конус в E ®k_E F.

ЗАМЕЧАНИЕ. Если E,F E (F), то из доказательства теоремы 2 видно, что для каждого z Е Е ®к_Е F ^и любого е > 0 существует элемент z^ Е К_а (где К_а — произвольный тензорный конус в Е ® F) такой, что хДгЕ К_а и к_ЕД^ < (1 + Е^к_ЕДУ

Если конус в F нормальный, то отсюда, вообще говоря, не следует нормальность конуса К_р (а значит, и произвольного тензорного конуса КД в Е ®k_E F.

ПРИМЕР 2. Пусть Е = I2 с конусом Ki, F = с₀ с обычным конусом. Ясно, что конус в со нормальный, однако К_р не является нормальным в Е ®k_E F, ^{так как в} противном случае конус положительных операторов в ГДЕ, ЕД [9] был бы несплю-щенным. В нашем случае £ДЕ,РД изоморфно пространству F^Ji), ^{так как} конус К^ в Z2 оштукатуриваемый [9]. В то же время оператор Т из примера 1 нельзя представить в виде разности положительных операторов.

Выясним, при каких условиях тензорный конус является оштукатуриваемым (телесным) в пространстве Е ®_а F, где а — произвольная кросснорма.

Теорема 3. Для того чтобы конус К_р был оштукатуриваемым в Е ®_а F необходимо и достаточно, чтобы Е₊ и F₊ были бы оштукатуриваемыми конусами в Е и F соответственно.

Доказательство. Необходимость. Пусть К_р — оштукатуриваемый конус в Е ®_а F. Возьмем х_ъ ... , х_п Е F₊, е Е F₊, ||е|| = 1 и рассмотрим элементы е ® х_Е ... , е ® ^ Е К_р. Тогда

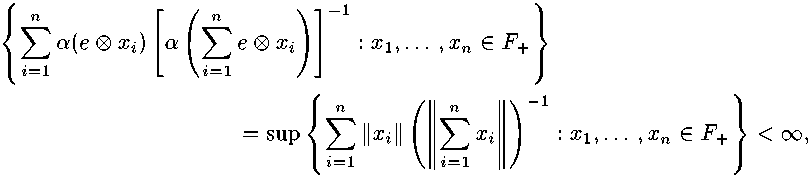
откуда следует, что константы нормальности конуса F+ ограничены в совокупности, следовательно, конус F+ оштукатуриваемый [2]. Аналогично доказывается оштукату-риваемость конуса F+.

ДОСТАТОЧНОСТЬ. Пусть / — равномерно положительный функционал на Е, g — равномерно положительный функционал на F. Тогда f 0 g — равномерно положительный функционал на (F ®а Е,КД. Действительно, пусть z = 52 ek ® $k G Кр, тогда где к — константа.

Теорема 4. Для того чтобы конус Ki был телесным в E®_aF, где a — любая кросснорма такая, что ct Д е, необходимо и достаточно, чтобы Е₊ был телесным конусом в Е и F₊ — телесным конусом в F.

Доказательство. Необходимость. Покажем, что F^ — телесный конус.

Пусть z = cr- ® $к — внутренняя точка конуса Ki в Е ®_а F, то есть ВД,Д С Ki, к = 1

где ВД,Д — замкнутый шар радиуса г > 0 с центром в точке z в Е ®_а F. Возьмем е Е Е^, ||е|| = 1. Тогда существует функционал Жд Е ЕД ||жд|| = 1 и (е,Жд) = 1.

Покажем, что ВД₀,Д С F₊, где ж₀ Е F, ж₀ = 52 к^ек,хДхк- Пусть у₀ Е F, ||у₀<  г. к=1

Положим z₀ = е ® уо- Тогда аДд) ^ ||у₀|| ^ т, отсюда z + z₀ Е K_a, следовательно

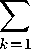
^к.ЛЛк + (е,жДу₀ Е F₊,

т, е. жо + уо Е F₊, значит, В До, г) С F₊.

Аналогично доказывается телесность конуса Е^.

Достаточность. Пусть u е F+ — внутренняя точка конуса Е+, v е К — внутренняя точка конуса F+. Тогда z0 = u® v является внутренней точкой конуса Ki.

Действительно, пусть шар ВД,рД С Е^, шар ВД,рД С F+. Возьмем произвольный элементz

= 52 ^ек ® Хк Е Е ® F такой, что а( fc=i

z — Z₀) ^ Р1Р2- Для любого / Е Е^.

имеем:

^кЛДк - ДЛЛ

< «Д - г0)|Д|| < P1P2II/II < Р^ЛЛ^, так как ||/|| < рт Ди,Д (см. [1, с. 29]). Поэтому

*\^екЛДк = (и,/)

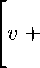
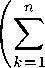
кекЛ^ДЛД

ЛЛГ

Е ДЛ^ВД^Д С F₊,

а это значит, что z

вк ® Хк Е Ki. Теорема доказана.

Приведем примеры, показывающие, что из того, что конуса F₊ и F₊ являются правильными (вполне правильными), вообще говоря, не следует, что произвольный тензорный конус в Е ®_ПЕ F {Е ®к_Е F) является правильным (вполне правильным).

Следует подчеркнуть, что в нашем более общем случае, когда Е является произвольным УБП, принадлежащем классу (F), в отличие от случая, когда Е — банахова решетка, в основном получаются отрицательные результаты, то есть здесь возникает существенно новая ситуация.

ПРИМЕР 3. Пусть Е = I2 с конусом F+ = Ку, таким же, как в примере 1, F = 1^ с естественным конусом. Конус F+ является оштукатуриваемым, следовательно, вполне правильным (см. [2, с. 9]). Конус F+ также вполне правильный, значит, правильный. Покажем, что, тем не менее, конус Кр в E®kBF не является правильным, следовательно, Кр не является вполне правильным в Е 0kE F- Рассмотрим последовательность элементов zu Е Е ® F, п = 1,2,..., определяемую следующим образом:

Я =

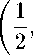
® (1, 0,... ); ^2 = ^1 +

^,0....

® (о, |,о,...

^п — ^п — 1 +

1,0,... ,0 1 О,--2’ ’       ’ ’ 2’ ’

® ( 0,... ,0, -,0,.

\         п

W -  - V

Ясно, что последовательность z_n возрастает. Кроме того, нетрудно видеть, что все г„ ограничены элементом (1,0,...) ® ^1, |,... , ^,... ^ . Однако последовательность z_n не является фундаментальной в Е ®ь_Е ^- Действительно, рассмотрим разность

^тг ^п

...+ (1о,...,1о,...)в(о,о,...,о,2.,о,...). x\e^^^—aNV„^^^w/      7     х\<^^.i^^^^™^      7

2п                         2п

Оценим норму кв^2п — z_n) снизу, воспользовавшись тем, что сопряженное (5 ®к_Е ^У канонически изометрично Е^Е₁ F*\ Так как конус в Е оштукатуриваемый, то всякий непрерывный оператор Т : Е —» F* является Z-оператором. Пусть Т '. 1^ ^ Ь, Т Е ^(^2,^2) — тождественный оператор. Нетрудно видеть, что ЦТф < \/2- Тогда

1 2n 1

М^"^^ Е ^

/с=п + 1

то есть последовательность z_n не фундаментальна; следовательно, К_р не является правильным в Е ®k_E Е.

ПРИМЕР 4. Пусть I2 упорядочено конусом

Е ^ж» < ^Ж1 ‘ • п = 2

К = ж = (жх,... , х_п,... ) : х_п ^ 0, Vn,

Положим Е = I2 с сопряженным конусом К*, тогда К* — замкнутый, нормальный, телесный, вполне правильный конус [2].

• 1)    Возьмем F = l^ с естественным конусом. Покажем, что проективный конус К_р не является вполне правильным в Е ®_ПЕ F. Рассмотрим последовательность z_n элементов из К_р\

^1 = (1, 0,... ) ® (1, 0,... ), zn = г„_1 + (0,... , 0,1,0,...) ® (0,0,... , 0,1,0,...).

Ясно, что последовательность z_u возрастает. Тем же методом, что и в примере 10 (см. [10, с. 231]) можно показать, что п-е^п^ ^ V^ для п = 1,2,.... Тем не менее, последовательность z_n не фундаментальна, так как n^f^+i — г„) = 1, то есть К_р не является вполне правильным в Е ®_ПЕ

• 2)    Возьмем F = I2 с конусом К*. Так как К* — телесный конус, то по теореме 4 инъективный конус Kj С E®F будет телесным конусом в Е ®_ПЕ ^- Покажем, что конус Ki не является правильным в Е ®_ПЕ F- Рассмотрим последовательность z_n, определенную в пункте 1 настоящего примера. Тогда z_n Е Ki, п = 1,2,... , последовательность z_H возрастает в смысле конуса Ki, tieVz^ ^ v2 для п = 1,2,... и не является фундаментальной. Следовательно, конус Ki в Е ®_ПЕ F не является вполне правильным. Тогда Ki не является правильным конусом в Е ®_ПЕ F, ^{так как} правильность и телесность конуса влекут полную правильность конуса (см. [2, с. 10]).

• 2° ) Пусть Е Е (7£), X — произвольное БП. Линейный оператор Т : Е —» X называется 1-оператором, если конечна /-норма:

  \\T\V = sup

  
  
  
  

  ||Те^|| : e_k Е Е₊, 1 <  к < п,

  

  < 1,п = 1,2,... | .

  
  

Пространство всех /-операторов из Е в X с /-нормой обозначим через ЕрЕ,Х\

Линейный оператор U : X —» Е называется Ьо- оператором, если он переводит единичный шар пространства X в порядково ограниченное множество в Е. Пространство всех Ьо-операторов из X в Е с Ьо-нормой

||/7||bo = inf{||e|| :[7Ж<е, Уж Е X, ||ж|| < 1} обозначим /фДХ, Е).

Теорема 5. Пусть E,F Е (7^.), X, Y — произвольные БП, S Е £\Е, X), S ^ 0, Т Е L(F, У), Т ^ 0. Тогда для любых кросснорм а и р оператор

S ®Т : ^Е^К^ дХ®3¥ является 1-оператором тогда и только тогда, когда S и Т суть 1-операторы. При этом

^РфЦтфЛЬЯИ < Р ® П, < ns]], \\t\v.

ДОКАЗАТЕЛЬСТВО. Пусть S : Е —> X — /-оператор. Это эквивалентно существованию функционала е* Е Ер, ||е*|| < 1 такого, что

Pell < PIHe*,e), VeES+:

аналогично, если Т : F —> Y — /-оператор, то найдется /* Е Fp, ]]/*|| ^ 1, такой что \\Tj\\ < ||Т||/(/,/*), V/ Е F+. Тогда е* ® /* — положительный непрерывный функционал, е*®ГЕ К*р. Пусть г =

£ ek ® fk Е Кр, к = 1

тогда

(5®Т)

Л"

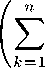
Sek ® Tf к

£||Sefc|| ||TA|| = £||S(efc||TA||)|| fc=i                     fc=i

£(efc,e*)||T/fc|| = ||S|hf;||T(/fc(efc,e*))|| fc=i                            fc=i уШГМЭДТьЕ^^А

Следовательно, S ®T — Z-оператор и ||S ® T\\t < ||5||г||Т||ь

Обратно, пусть S ® T : (E ®_a F,K_P^ -д X ®₃ Y — Z-оператор. Покажем, что

S и T Z-операторы. Пусть ei,... , еп Е Е+. Возьмем / Е F+, Т/ ^ 0. Тогда ei ® /,..., еп ® / Е Кр. Поскольку S ® Т Z-оператор, то r/||£||Sefc|| =£/3[(S®T)(efc®/)], fc=i            fc=i

||5®Т|И

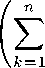
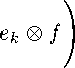
= ||S®T||Z

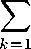
MW

Значит, S — Z-оператор и ||S||z < ||S ® Т||г||/||(||Т/|| ^x). Отсюда, так как последнее неравенство верно V/ Е F₊, ||/|| = 1, то ||S||z < ||S ® T\\t • ||Т||^-1, откуда ||S ® T\\t ^ Р1М1ТЦ.

Аналогично получаем, что \\T\\i < ||S ® T\\i • ||S|| ¹ и ||S ® T\\i ^ \\T\\i ||S||. Итак, \\s®t\v > vWW^mW-

Теорема полностью доказана.

Теорема 6. Пусть F,F(F), X, Y суть произвольные БП, U Е C^X,EY U ^ 0, V Е ИУ,ЕЗ V ^ 0. Тогда для любых кросснорм а ^ е и р ^ е оператор

U ®V : X ®aY ^ (Е ®3 Е,КЗ является Ъо-операторов тогда и только тогда, когда U nV — Ьо-операторы. При этом

ЛЖТййЛтЖ < г ® viibo < riiboiMibo.

Доказательство. Пусть U ; X —> Е и V ; Y —> F — Ьо-операторы. Тогда найдутся элементы е Е F₊ и / Е F₊ такие, что

EUx^e, ^хЕХ, h||bo = inf{||e||}: FVy^J, VyEY, ||у||<1; ||И||_Ьо = inf{||/||}.

Покажем, что оператор U 0 V : X 0_а Y д (Е ®р Е,К^ является Ьо-оператором при а = е (а значит, при любом а ^ е\ Пусть z Е X ® У, z = 52 ^xk ® Uk и e(z) < 1. fc=i

Докажем, что YU ® V(z) < е ® / в смысле конуса К_г, т. е.

!^Ux_k®Vy_kl е*®Г^ < (е,е*)(/,/*), Ve* Е S;, V/* Е F/.

При этом достаточно считать, что V* f* ^ 0. Имеем:

Yw^-w^n = (и Ё^№,/•> ,=•)

fc=l                           \ \fc=l               /     /

<

^x_k\Vy_klO =(е,еД sup i                        Ik* К

Кроме того,

(Vy_kln = (ул v\n = ^дтт^ЖЧЧ

II^TII = sup (У7*,У)| = sup |(/*,Ky)K (/,/*).

Далее получаем:

(е,еД sup

= (е,е*) sup

»-^) 1ЛЛ

< (e,e*)||y*/*||sup

Итак, ЦП® У||ьо < inf{||e|| ||/||} < ||H||bo ||K||bo.

Обратно, пусть U ® V : X ®_а Y -д ^Е®р,К^ — Ьо-оператор. Покажем, что U : X —> Е также является Ьо-оператором. Возьмем / Е УД II/* II = 1- Пусть х Е X, ||ж|| < 1 и у Е Y такой, что ||у|| = 1 и (Уу,/Д > 0. Тогда найдется элемент z Е К^

z = 52 ek ® fk такой, что Ux ® Vy < z в смысле конуса К,. Отсюда fc=i

Ux <

Тогда

Mbo <

(V^OPK <  sup

Переходя к супремуму по всем у Е У, ||у|| = 1 и всем /* Е F^, ||/*|| = 1, получим: ||У||Г11ьо^Г^У||ьо.

Аналогично доказывается, что ||И|| ||У||ь0 ^ II ^ ® У||ьо, т. е.

Р® Пь0 > Л^ЫМй ЛЙЖ

Теорема полностью доказана.