Конвективная неустойчивость в двухслойной системе реагирующих жидкостей с диффузией, зависящей от концентрации компонентов

Первое экспериментальное наблюдение хемогидродинамического структурообразования, возникающего в системе двух реагирующих жидкостей, было осуществлено, вероятно, ещё в 1888 году Д. Квинке [1]. Он привел в соприкосновение масляный раствор лауриновой кислоты и водный раствор гидроксида натрия и в ходе реакции нейтрализации увидел спонтанную эмульсификацию на поверхности раздела. Однако по-настоящему последовательное и подробное изучение взаимодействия процессов диффузии–реакции и гидродинамических явлений началось только через сто лет, что было обусловлено появлением важных технологических приложений, среди которых можно выделить нефтепереработку [2], процессы горения [3], сепарацию урановых руд [4] и другое.

Отметим, что особый интерес исследователей к взаимному влиянию химических реакций и тепломассопереноса в жидкостях происходит из факта, что реакции могут вызывать существенные изменения таких физических свойств жидкостей, как плотность, вязкость, теплопроводность и поверхностное натяжение. Это, в свою очередь, способствует формированию диссипативных структур нового типа, преобразующих исходное распределение реагентов вплоть до смены характера реакции.

В последние годы внимание большого числа исследователей приковано к изучению гидродинамики экзотермической реакции нейтрализации. Интерес стимулируется сравнительно простой, хотя и нелинейной кинетикой реакции и перспективой многочисленных приложений. Как оказалось, развитие реакции в несмешивающихся и смешивающихся системах существенно различается. Случаи двухслойной системы несмешивающихся реагирующих растворов рассмотрены в [5–11]. Сюда можно отнести и работы по изучению хемосорбции двуокиси углерода щёлочью, поскольку реализуется та же кинетика реакции нейтрализации [12, 13], которая протекает на межфазной границе «газ–жидкость». В частности, в серии экспериментальных работ [5–6, 8] описаны новые эффекты, связанные с взаимодействием экзотермической реакции нейтрализации и поверхности раздела «жидкость–жидкость» двухслойной системы, помещённой в ячейку Хеле-Шоу. Один слой данной системы образует кислота, растворенная в органическом растворителе, а другой представляет собой водный раствор щёлочи. Авторы статьи выяснили, что, меняя тип реагентов и их начальные концентрации, можно получать различные структуры. Например, в работе [5] в ходе реакции кислоты карбоновой группы (спиртовой раствор) с водным раствором гидроксида натрия обнаружено неупорядоченное распространение пальцевидных конвективных структур (fingers в англоязычной литературе) в нижнем слое, что является типичным для такого рода систем. И, в силу того, что поступающая из верхнего слоя кислота тяжелее основания, поведение системы легко объяснялось неустойчивостью Рэлея–Тейлора [6, 7]. Подобное структурообразование имело место и в нижней (жидкой) фазе при хемосорбции CO ₂ щёлочью [12], что также может быть связано с развитием указанной неустойчивости [13].

Однако исследователей ждал сюрприз — в [8] авторы эксперимента получили идеально периодическую систему хемоконвективных ячеек, медленно растущих от поверхности раздела. Они приводили в контакт раствор пропионовой кислоты и водный раствор более сложного основания — тетраметилового гидроксида аммония (TMAH). В рамках построенной теоретической модели в [9] удалось показать, что необычную регулярность системе придаёт баланс между неустойчивостями Рэлея–Тейлора и Рэлея– Бенара. При несмешивающихся растворах важную роль в формировании конвективного течения могут играть также поверхностные механизмы неустойчивости, связанные с деформацией межфазной поверхности [10], изменением поверхностного натяжения вследствие либо тепловыделения [11], либо разности концентраций реагентов [11], либо различной скорости процессов адсорбции–десорбции [14]. Перечисленные эффекты участвуют в тонкой настройке конфигурации хемоконвективных ячеек, выравнивая их вдоль поверхности раздела сверху и по кончикам солевых пальцев снизу.

Совершенно другая ситуация наблюдалась до последнего времени в смешивающихся системах реагирующих жидкостей [15–19]. Здесь в отсутствие межфазной границы в качестве главной причины развития хемоконвекции выступают гравитационные механизмы движения, обусловленные формированием зон с неустойчивой стратификацией по плотности вследствие разной скорости диффузии реагентов [15, 16]. В бинарных системах в зависимости от соотношения коэффициентов диффузии компонент выделяют неустойчивость двойной диффузии ( Double-Diffusion Instability или, для краткости, DD конвекцию), неустойчивость диффузионного слоя ( Diffusive Layer Convection или DLC конвекцию) и запаздывающую неустойчивость двойной диффузии ( Delayed Double-Diffusion Instability или DDD конвекцию). При описании необходимо также учитывать появление третьей компоненты — продукта реакции, который формируется на фронте реакции и диффундирует в объёмы исходных реагентов, что также может провоцировать появление неустойчивости типа двойной диффузии. В результате серии как экспериментальных, так и теоретических работ [16–19], посвященных изучению этих явлений, были обнаружены хемоконвективные структуры с высокой степенью нерегулярности солевых пальцев, которые распространялись в обе стороны от линии соприкосновения слоёв.

Отметим, что абсолютно все известные авторам работы по хемоконвекции предполагают постоянство коэффициентов диффузии реагентов, в то время как реальные коэффициенты диффузии всегда зависят от концентрации раствора. Однако в механике жидкостей эта зависимость, как правило, считается настолько слабой, что ею пренебрегают. Редкие примеры рассмотрения концентрационно-зависимых коэффициентов диффузии можно найти лишь в чистых задачах реакции–диффузии без конвекции (см., например, [20, 21]), но даже здесь наблюдаются только количественные, но не качественные изменения.

Данная статья является продолжением работы [22] и посвящается смешивающимся реагирующим системам, в которых впервые выявлено структурообразование в виде идеально периодической системы хемоконвективных ячеек, формирующихся параллельно фронту реакции и перпендикулярно направлению силы тяжести. Показано, что возникновение макроскопического движения жидкости связано со специфическим механизмом неустойчивости, который обусловлен зависимостью коэффициентов диффузии реагентов от их концентраций. Так как этот тип неустойчивости описывается в литературе впервые, то авторами она названа неустойчивостью концентрационно-зависимой диффузии ( Concentration-Dependent Diffusion Instability или CDD конвекцией). В работе теоретически и экспериментально изучаются некоторые свойства нового типа неустойчивости, а также обсуждаются причины, почему CDD конвекция оставалась до сих пор неизвестной. Впервые обсуждается существование конвективных ячеек, окруженных толщей квазинеподвижной жидкости.

• 2.    Теоретическое описание CDD конвекции

  • 2.1.    Математическая модель

В силу того, что явление существенно зависит от законов диффузии, которым подчиняются реагенты, теоретическое описание проведём для конкретной системы. Пусть две смешивающиеся жидкости в начальный момент времени заполняют верхний и нижний слои в ячейке Хеле-Шоу. Верхний слой — это водный раствор азотной кислоты HNO 3 , концентрацию которой обозначим A , а нижний — водный раствор гидроксида натрия NaOH с концентрацией B . С точки зрения химической кинетики в этой системе происходит следующее. Кислота в водном растворе диссоциирует на катион гидроксония и анион кислотного остатка:

NO2 OH + H2O ^ NO2 O- + H3O+ , а основание распадается следующим образом:

NaOH ^ Na ⁺ + OH - .

Далее, катионы H 3 O ⁺ находят анионы OH и образуют воду, в то время как катионы основания, встречаясь с анионами кислотного остатка, образуют соль (нитрат натрия с концентрацией S ):

NO 2 O - + Na ⁺ ^ Na NO 3 .

Таким образом, на границе контакта растворов происходит реакция нейтрализации, которая, вообще говоря, сопровождается выделением теплоты. Однако в данной работе ограничимся рассмотрением изотермической задачи, и эффект тепловыделения в уравнениях не будет учитываться. Это допущение основывается на данных экспериментов, и, кроме того, стенки кюветы всегда можно сделать достаточно теплопроводными, чтобы тепло диссипировало, не оказывая существенного влияния на процессы. В результате кинетика реакции (1) упрощённо может быть представлена как

A + B ^ S.

Так как оба реагента растворены в воде, то при приведении в контакт первоначально разделённых слоёв начинается их смешивание. Необходимо отметить, что задача является неавтономной, поскольку в ходе реакции реагенты не пополняются, а профили концентраций необратимо меняются.

Перечислим основные предположения, сделанные при выводе теоретической модели:

• –    зазор h между широкими стенками настолько мал, что течение жидкости в рамках приближения Хеле-Шоу считается почти двумерным;

• –    свойства жидкостей не зависят от концентрации реагентов за исключением указанного ниже случая;

  – задача является изотермической;

• –    скорость реакции нейтрализации постоянна и равна K ;

• –    начальные концентрации кислоты A ₀ и основания B ₀ одинаковы.

Пусть координаты x и z проходят вдоль широких граней ячейки Хеле-Шоу так, что линия z = 0 задаёт начальную контактную поверхность между слоями. Границы ячейки определим как 0 <  x <  H , - L <  z <  L . Выберем в качестве единиц измерения длины — h , времени — h²/Da ₀ , скорости — D _{a 0}/ h , давления — p ₀ v D_{a 0}/ h² , концентрации — A ₀ . Здесь: D_{a 0} — табличное значение коэффициента диффузии азотной кислоты в воде при температуре 25 ° C; р ₀ и v — плотность и коэффициент кинематической вязкости воды соответственно.

С учётом сделанных предположений уравнения конвекции–реакции–диффузии в приближении Хеле-Шоу в безразмерной форме принимают вид:

х ГдФ+ 6 _М ^_ф- 12 _ф- R a а л - R b a s - R ^ d s , Sc (d t 5 d ( z , x ) )                  d x d x d x

— + a ⁽ ¥ , A ) =_v D ( A ) _v A - a Aв , a t d ( z , x )        a

SB + S(¥,B) =vD (в)vв - aAB , d t d( z, x)       b as д(т,s) a t d(z, x)

=V D_s ( S ) V S + a A B .

Использована двухполевая запись уравнения движения и введены функция тока Т и завихрённость Ф = -ДТ , а реакционные слагаемые появились на основании кинетического уравнения (2). Уравнение (3) отличается от стандартного уравнения Навье–Стокса наличием дополнительного слагаемого, пропорционального завихрённости, которое описывает гидродинамическое сопротивление широких граней ячейки Хеле-Шоу. Действие граней аналогично силе Дарси в пористой среде. Диффузионные слагаемые в уравнениях (4)–(6) представлены в наиболее общей форме [23], допускающей зависимость коэффициентов от концентрации соответствующих веществ.

К уравнениям (3)–(6) добавим граничные условия:

z = ± L :	Т = 0, — = 0, — = 0, — = 0, — = 0,                 (7) д z        д z        д z        д z
x = 0, H :	Т = 0, — = 0, — = 0, — = 0, — = 0                (8) д x       д x       д x       д x
и начальные условия при t = 0:	z <  0: Т = 0, A = 0, B = 1,                                     (9) z >  0: Т= 0, A = 1, B = 0.                                  (10)

В задаче (3)-(10) присутствует несколько безразмерных параметров: Sc, а , R i .

Число Шмидта Sc = v/ D a ₀ является отношением характерного времени диффузии кислоты к характерному гидродинамическому времени. Оценка рассматриваемой системы даёт значение Sc « 10 ³ . Вообще говоря, такое значение позволяет отбросить в уравнении (3) левую часть. Однако, с точки зрения вычислительной процедуры, проще и эффективнее решать нестационарное уравнение движения, чем производить итерирование в ходе решения уравнения Пуассона. Поэтому нелинейное слагаемое в (5) не отбрасываем, хотя большое значение числа Шмидта накладывает особое условие на величину шага по времени.

Число Дамкёхлера а в уравнениях (4)-(6) — это отношение диффузионного времени к характерному времени протекания реакции. Известно, что реакция нейтрализации проходит очень быстро: оценка даёт значение а « 10 ³ .

В уравнении (3) величины концентрационных чисел Рэлея R i = g в Ah ³/( v D_{a 0} ) , где i = { a , b , s } , взяты на основании экспериментальных данных (см. раздел 3): R _a = 1,5 - 10 ³ , R _b = 1,8 - 10 ³ ,R _s = 2,4 - 10 ³ . Все численные результаты, представленные ниже, были получены при этих фиксированных параметрах.

В ходе исследования удалось обнаружить, что зависимость коэффициентов диффузии от концентраций в данной системе и определяет структурообразование. Чтобы найти вид функциональных зависимостей, стоящих в уравнениях (4)–(6), для системы водных растворов HNO 3 /NaOH был произведён поиск данных для коэффициентов диффузии в литературе. Сводный график обнаруженных экспериментальных результатов [24–30] показан на рисунке 1 для диапазона концентраций, в котором выполнялся эксперимент (см. раздел 3). Из рисунка хорошо видно, что зависимость коэффициентов диффузии имеет, вообще говоря, нелинейный характер. Для простоты, ограничиваясь лишь линейной аппроксимацией, в рассматриваемом диапазоне концентраций до 3 моль/л получаем следующие безразмерные выражения:

D_a ( A ) « 0,158 A + 0,881,    D_b ( B ) «- 0,087 B + 0,594,    D s ( S ) «- 0,284 S + 0,478,        (11)

• в    то время как постоянные табличные значения коэффициентов составляют:

D a^ab = 1,0,     D b^ab = 0,68,     D‘“^b = 0,5.                                   (12)

Выражения (11), (12) обезразмерены с помощью табличного значения коэффициента диффузии азотной кислоты 3,15 - 10 ^{- 5} см²/с. В предельном случае нулевых концентраций формулы (11) не приводят к табличным значениям (12) по причине сильно нелинейного поведения зависимостей при малых значениях концентрации (Рис. 1). Однако этим можно пренебречь, поскольку реальный интерес представляет область бόльших начальных концентраций реагентов.

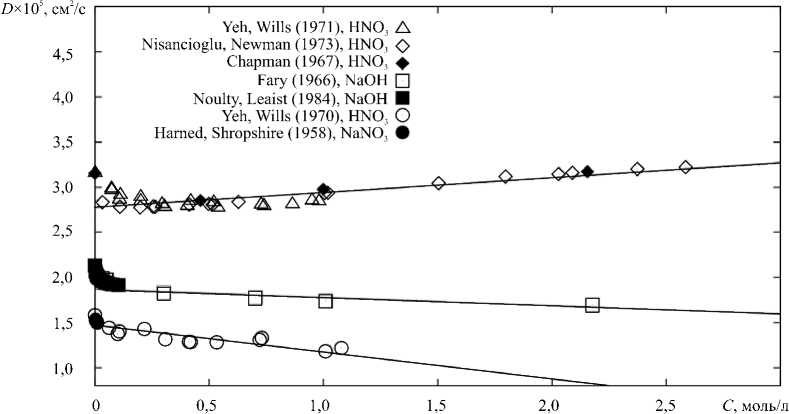
Рис. 1. Сводный график зависимости коэффициентов диффузии азотной кислоты (маркеры △ , о , ♦ ), гидроксида натрия ( ■ , □ ) и нитрата натрия ( о, •) от их концентраций при температуре 25 ° C , составленный на основании экспериментальных данных из работ разных авторов [24–30] в диапазоне концентраций до 3 моль/л; сплошные линии – линейные аппроксимации соответствующих экспериментальных данных методом наименьших квадратов

Как хорошо видно из рисунка 1, молекулы щёлочи и соли с ростом концентрации диффундируют медленнее, в то время как процесс диффузии кислоты наоборот ускоряется. Так как в пределах каждого элемента жидкого объёма концентрации реагентов и продукта реакции весьма различаются, то для анализа его движения удобно ввести величину полной безразмерной плотности:

р ( x , z ) = R a A ( x , z ) + R ь B ( x , z ) + R _sS ( x , z ).

Таким образом, в задаче (3)–(11) значения всех безразмерных параметров определены.

• 2.2.    Основное состояние реакции–диффузии и его линейная устойчивость

Система уравнений (3)–(11) допускает важный класс нестационарных решений, которые описывают динамику процессов реакции–диффузии. Жидкость при этом остается в состоянии механического равновесия, которое будем называть основным. Положим в (3)–(11) скорость жидкости равной нулю и будем определять поля концентраций, зависящие только от вертикальной координаты и времени: A ⁰( z , t ) , B ⁰( z , t ) , S ⁰( z , t ) . Получающуюся нелинейную нестационарную задачу

0        20 — = D (A °) ^A d t a      d z z , dDa (A °) dA ° d z   8 z -aA0 B 0, (14) dB° _D(Ro. d2B0 at " D(B ) a? 8Db(B°) 8B0 8 z    8 z -aA0 B 0, (15) = Ds (S 0) d^ d t           d z 8Ds(S°) 8S0 8 z   8 z + aA0 B0 (16) дополним граничными и начальными условиями (7)–(10). Данная задача не имеет точного решения и может быть разрешена только численно. Метод решения обсудим ниже.

На рисунке 2 а для трёх последовательных моментов времени приведены профили полной безразмерной плотности (13), вычисленные для основного состояния (14)–(16). В начальный момент времени конфигурация системы полностью устойчивая: водный раствор азотной кислоты находится над водным раствором более тяжёлого основания (Рис. 2 а , t = 0). Сразу после начала реакции характер профиля плотности резко меняется — появляются два локальных минимума. Если определить фронт реакции как линию в пространстве, на которой концентрации кислоты и основания равны, а реакция происходит наиболее интенсивно (каждая молекула кислоты встречает молекулу основания), то один минимум расположится выше фронта реакции, а другой — ниже (Рис. 2 а , t = 3). В дальнейшем профиль качественно сохраняется, хотя под действием диффузии несколько растягивается по вертикали (Рис. 2 а , t = 10).

Появление верхнего минимума легко находит своё объяснение в рамках DLC неустойчивости, которая является разновидностью неустойчивости двойной диффузии. Этот тип неустойчивости впервые введён в механику жидкости в работе [15], где рассматривались безреакционные задачи. Если в поле силы тяжести в начальный момент времени более легкая жидкость находится над более тяжёлой жидкостью, но при этом значение коэффициента диффузии верхнего элемента больше, то происходит следующее [15, 16]: верхний элемент, несмотря на устойчивость конфигурации системы в самом начале эволюции, диффундирует вниз быстрее. Вследствие этого выше линии соприкосновения слоёв растворов создается зона, обедненная веществом (зона с минимумом плотности). При этом ниже, симметрично относительно линии первоначального соприкосновения, появляется зона перенасыщенная веществом (зона с максимумом плотности). Эти зоны разделены узкой зоной смешивания, где конфигурация плотности остается устойчивой. Минимум плотности вверху порождает конвективный поток жидкости вверх (концентрационные плюмы). Симметрично этому внизу, где сформировался максимум плотности, возникает конвективный поток вниз (концентрационные пальцы). В силу того, что сама система не может сбалансировать распространение этих структур, то они развиваются до тех пор, пока течением не достигается граница ячейки. При этом распространение пальцевидных структур и плюмов характеризуется высокой степенью неупорядоченности.

Отметим, что в изучаемой системе изначально имеются условия для зарождения DLC неустойчивости, поскольку коэффициент диффузии расположенной сверху более легкой кислоты примерно в полтора раза больше, чем у основания (Рис. 1). Однако в условиях реакции в дело вступает третий компонент — продукт реакции (соль), который нарушает сценарий. Соль является самой тяжёлой из трёх растворенных веществ ( R s >  R b >  R a ), но одновременно и самой малоподвижной, так как обладает наименьшим коэффициентом диффузии (12). Вследствие этого в ходе реакции соль предпочитает накапливаться вблизи фронта реакции, слабо диффундируя из этой области. Однако только этих очевидных аргументов недостаточно, чтобы объяснить необычный вид профиля плотности, представленного на рисунке 2 а .

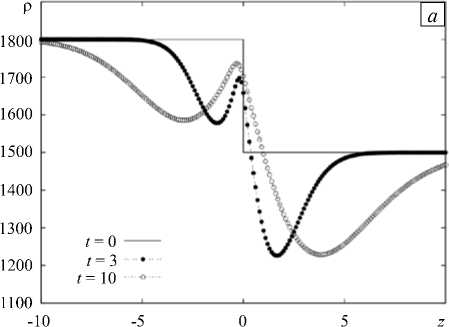
Рис. 2. Эволюция профиля полной безразмерной плотности (13) для трёх последовательных моментов времени t ( а ); профили плотности в момент времени t = 3 при постоянных коэффициентах диффузии реагентов (кривая 1 ) и с учётом концентрационно-зависимой диффузии ( 2 ) ( б )

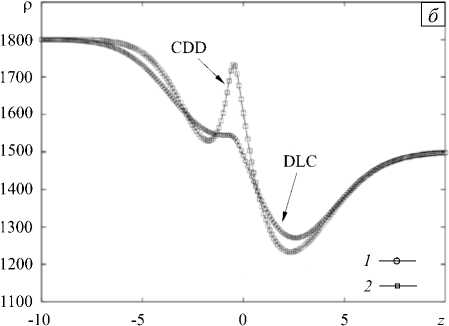
На рисунке 2 б приведены профили полной плотности, вычисленные при постоянных коэффициентах диффузии веществ (12) (кривая 1 ) и с использованием данных, полученных с помощью функциональных зависимостей (11) (кривая 2 ). Хорошо видно, что в первом случае профиль плотности хоть и отличается от известного профиля для классической DLC неустойчивости, но не качественно. И только учёт зависимости коэффициентов диффузии от концентрации делает возможным получение локального максимума плотности на фронте реакции (Рис. 2 б ; кривая 2 ), качественно изменяющего структурообразование в системе.

Анализ рисунка 1 позволяет понять, что происходит в ходе реакции. Вначале на фронте выделяется соль, количество которой со временем растет. При этом с увеличением концентрации коэффициент диффузии соли заметно уменьшается, что препятствует её отводу из области фронта реакции. Однако накопление соли не ведет к прекращению реакции, так как быстро диффундирующая кислота проникает в зону, расположенную ниже фронта реакции, а с ростом концентрации азотной кислоты коэффициент её диффузии только увеличивается. Таким образом, второй минимум плотности возникает исключительно благодаря концентрационной зависимости коэффициентов диффузии. Для названия связанной с ним конвективной неустойчивости предлагаем термин « неустойчивость концентрационно-зависимой диффузии — CDD конвекция». Минимум плотности, расположенный выше фронта, и связанные с ним восходящие концентрационные плюмы имеют традиционное происхождение — это проявление DLC механизма.

Рассмотрим вопрос об устойчивости основного состояния (14)–(16) по отношению к малым монотонным возмущениям:

Ф ( t , x , z ) ¥ ( t , X , Z )

A ( t , x , z ) B ( t , x , z ) S ( t , x , z )

■ 0 "		ф ( t , x , z )
0		ф ( t , x , z )
A °( t , z )	+	a ( t , x , z )	exp( I kx ) ,
B 0 ( t , z )		b ( t , x , z )
_ S 0 ( t , z ) _		_ s ( t , x , z ) _

где ф , ф , a, b, s — соответствующие амплитуды возмущений, k — волновое число, I — мнимая единица.

Подставляя разложения (17) в уравнения (3)–(10) и линеаризуя последние около основного состояния (14)–(16), получаем следующую систему нестационарных амплитудных уравнений для определения критических возмущений

—^ = Aq- 12ф-k2 (R a + R b + R s),(18)

Sc dt da                 dDa(A0)(^8A0(z,t) da    82 A0(z,t))           x. Doz x      8A0(z,t)

— = D ( A ⁰ ) A a +--- a²--² 2--- —— — + a----V-² -a A ⁰ ( z , t ) b -a B ⁰ ( z , t ) a + ф--- ²²², (19)

8t    a            dA0 (    8z    8z       8z2   )                                dz’ db                dDb(B0)MB0(z,t) db Ld2B0(z,t))                 Doz x      dB0(z,t)

— = D_h ( B ⁰ ) A b + — b²—² 2--- — + b---- ²²² -a A ⁰ ( z , t ) b -a B ⁰ ( z , t ) a + ф--- ²²², (20)

81 b            dB0 (     dz    8z       8z2   J5

8 s                 dD_s ( S ⁰ ) (nd S ⁰ ( z , t ) 8 s     8 ² S ⁰ ( z , t ) )                  _d0, _x       8 S ⁰ ( z , t )

= D ,( S ⁰ ) A s +    s²-² 2 + s +a A ⁰ ( z , t ) b + a B ⁰ ( z , t ) a + ф (21)

8t s           dSQ ( 8z 8z       8z2   J с граничными условиями z = ±L : ф = 0, V = ^ = 0, a = 0, b = 0, s = 0,(22)

d x x = 0, H : ф = 0, ф = —= 0, a = 0, b = 0, s = 0.(23)

8 x

Здесь A^d ²/ 8 z ² - k ².

Итак, полная спектрально-амплитудная задача включает в себя уравнения для определения возмущений (18)–(23), систему уравнений для нахождения основного состояния (14)–(16), а также законы диффузии (11). Нестандартной особенностью полученной задачи является нестационарный характер не только самих амплитуд возмущений, но и основного состояния (14)–(16). Для решения задачи использовался метод Initial Value Problem (IVP) [11]. Известно, что метод даёт адекватные результаты всегда, за исключением короткого начального периода времени, когда основное состояние быстро меняется. В рассматриваемой в данной статье задаче проблема начального времени разрешается сама собой, так как критически растущие возмущения появляются только спустя некоторое время после начала эволюции, заведомо большее времени релаксации в методе IVP.

Общая схема численного анализа включала совместное интегрирование по времени методом конечных разностей уравнений основного состояния (14)–(16) и малых нормальных возмущений (18)–(23) для фиксированного волнового числа. В процессе эволюции вычислялась величина Х ( t ), которая фактически имеет смысл показателя Ляпунова:

1 "  1     a, ( t + A t )

Х( t ) = —У—ln ----

N j = 1 A t     a j ( t )

где A t — шаг интегрирования, N — количество независимых реализаций (обычно 10-15), a ( t ) — возмущения поля концентраций кислоты. Каждое независимое интегрирование системы начиналось со случайных начальных условий для всех возмущений с амплитудой не более 10^-4. Наступление неустойчивости (или выход из нее) фиксировалось по изменению знака инкремента Х ( t ), усреднённого по реализациям.

0,01

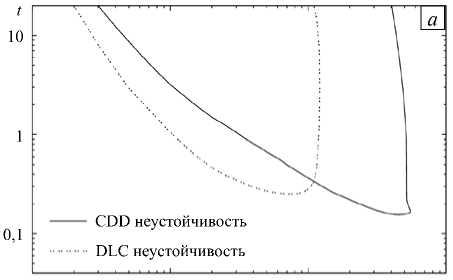
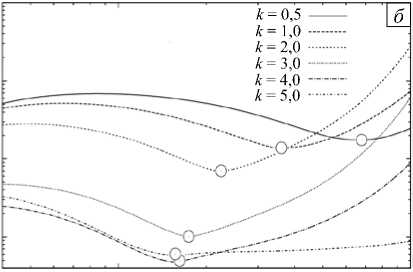
Рис. 3. Нейтральные кривые для двух мод неустойчивости: конвекция диффузионного слоя (штриховая линия) и неустойчивость CDD (сплошная линия) ( а ); эволюционная зависимость максимального значения возмущения функции тока ψ для разных значений волнового числа в случае CDD ( б )

од

На рисунке 3 а приведён график нейтральных кривых для DLC неустойчивости (штриховая линия) и CDD неустойчивости (сплошная линия). Поскольку система неавтономна, то время выступает здесь как параметр задачи. Из рисунка видно, что в самом начале эволюции обе моды устойчивы. В момент времени t ≈ 0,15 первым теряет устойчивость возмущение с волновым числом k ≈ 4,6 , отвечающее концентрационно-зависимой диффузии. DLC неустойчивость возникает примерно при t ≈ 0,25 и характеризуется критическим волновым числом k ≈ 0,75 . Это связано с тем, что наклон профиля плотности для DLC неустойчивости меньше (Рис. 2 а ). Существенное различие длин волн начальных возмущений объясняется разной шириной зон неустойчивости (Рис. 2 а ). Со временем обе неустойчивости смещаются в сторону более длинных волн, что отражает факт постепенно расширения конвективной зоны за счёт диффузии.

Скорость роста возмущений в зависимости от волнового числа можно оценить по рисунку 3 б , на котором изображена эволюция максимального значения возмущения функции тока для CDD неустойчивости. Хорошо видно, как при входе внутрь мешка неустойчивости возмущения начинают расти экспоненциально.

• 2.3.    Результаты численного расчёта полной нелинейной задачи

Перейдем к обсуждению результатов прямого численного моделирования задачи (3)–(11). В данной работе для получения численного решения применялся метод конечных разностей, детальное описание которого приведено в работе [9]. В данном случае общая схема расчёта даже проще, так как жидкости смешиваются, и свободная поверхность отсутствует. Использовалась явная схема, в которой устойчивость метода обеспечивалась выбором шага по времени в виде:

∆t =

∆ z ²

2(2 + max( Ψ , Φ )) ^.

Точность интегрирования уравнения Пуассона составляла 10 ^{- 4} . Расчёты производились на однородной сетке, в которой на единичную квадратную область приходилось 6 × 6 узлов ( ∆ x =∆ z = 0,2 ). Такое разрешение выбрано на основании предыдущего опыта численного моделирования хемоконвективных структур в расчётной области подобной геометрии [6–7, 9]. В качестве начального условия задавалось случайное распределение поля функции тока с амплитудой не более 10 ^{- 3} .

Рисунок 4 демонстрирует изолинии завихрённости и поле полной плотности среды в момент времени t = 3 , когда оба типа возмущений уже сформировались и стали конечными. Важной особенностью системы является независимость неустойчивостей: оба типа возмущений возникают в разных частях расчётной области и практически не взаимодействуют друг с другом в начале эволюции. Обнаружено, что первым возбуждается конвективное движение ниже первоначальной контактной линии (линия с координатой z = 0 на рисунке 4). Длина волны возмущения в начальный момент времени находится в полном согласии с результатами линейного анализа (см. Рис. 3). Поле плотности на рисунке 4 б иллюстрирует нелинейность развития возмущений: если в самом начале эволюции слой сравнительно тяжёлой жидкости нависает над слоем более легкой, создавая условия для появления неустойчивости, то уже к t = 3 ниже линии z = 0 формируется система солевых капелек. Так как максимум плотности вблизи фронта реакции локальный, то структура выравнивается благодаря располагающейся снизу более плотной среде. Таким образом, наблюдается локальное хемоконвективное движение в области между

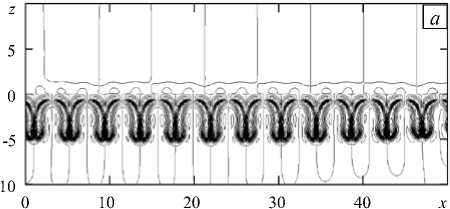
Рис. 4. Поля завихрённости Ф ( x , z ) ( а ) и полной плотности р ( x , z ) ( б ) в момент t = 3 , полученные в результате численного решения полной нелинейной задачи (3)–(11) для фронтальной реакции нейтрализации

^^^^^^^^^^^^^^^^^^^ I I —I

1200   1300   1400   1500   1600    1700   1800 1900

двумя массивами неподвижной жидкости (это хорошо видно на рисунке 4 а ). Как уже отмечалось выше, полоса неустойчивости медленно расширяется вследствие диффузии реагентов (см. Рис. 2), — точно в меру этого расширения происходит и движение вниз обогащённых тяжёлой солью пальцевидных структур. В верхней полосе неустойчивости формируется традиционное конвективное движение в виде всплывающих концентрационных плюмов. Их продвижение вверх очень быстро становится неупорядоченным и ограничивается только размером расчётной области. Отметим, что конвекция верхнего диффузионного слоя (DLC неустойчивость) имеет бóльшую длину волны и в начале эволюции оказывает слабое влияние на вид концентрационных полей (Рис. 4). Обе неустойчивости разделены тонкой прослойкой практически неподвижной жидкости, которая может деформироваться, но сохраняет целостность в условиях конвекции. Её существование обусловлено наличием узкой зоны над фронтом реакции, имеющей устойчивую конфигурацию профиля плотности (Рис. 2).

Численное исследование фронтальной реакции нейтрализации (Рис. 4) выявило замечательный факт: хемоконвекция может зародиться и существовать достаточно долго в локальной области массива неподвижной сплошной среды. Это становится возможным благодаря формированию плотностного «кармана», внутри которого и развивается конвекция.

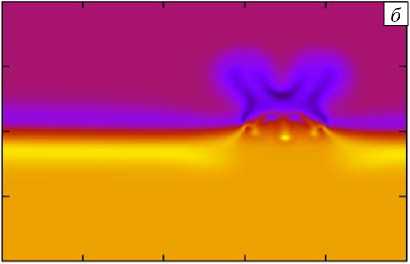
Формирование локализованной конвективной структуры весьма непривычно для исследователей, занимающихся классической тепловой конвекцией, которая быстро охватывает всё рабочее пространство кюветы. Для моделирования хемоконвективной ячейки, ограниченной плотностными барьерами со всех сторон, был произведён расчёт для реакции, происходящей лишь на определённом участке контактной линии. Эта постановка задачи воспроизводит ситуацию, когда в толще двух смешивающихся, но не реагирующих жидкостей навстречу друг другу движутся струи двух реагентов, плотности которых совпадают с плотностью соответствующих слоёв. Реагенты натекают друг на друга (кислота — сверху, а основание — снизу) в полосе 30 <  x <  40. Таким образом, в начальный момент времени реакция протекает только на пересечении указанной полосы и контактной линии z = 0 . В дальнейшем диффузия реагентов приводит к объёмной реакции. На рисунке 5 показаны изолинии завихрённости и поле полной плотности среды в момент времени t = 3 . Хорошо видно, что краевые эффекты сказываются на форме фронта реакции, ниже которого по-прежнему локально возникает CDD неустойчивость, а выше развиваются два всплывающих плюма DLC конвекции (Рис. 5 б ). Наиболее сильные конвективные вихри характерны для верхнего слоя, где имеют место вертикально ориентированные перепады плотности (Рис. 5 а ).

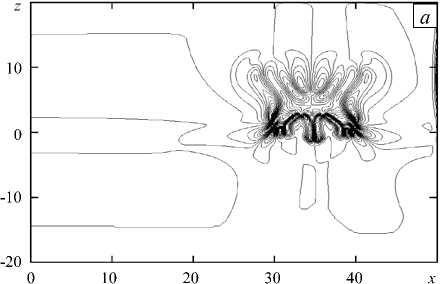
Рис. 5. Поля завихрённости Ф ( x , z ) ( а ) и полной безразмерной плотности р ( x , z ) ( б ) в момент t = 3, полученные в результате численного решения полной нелинейной задачи (3)–(11) для реакции нейтрализации, происходящей лишь на участке 30 <  x <  40 контактной линии

ю о

-ю

-20

1200   1300   1400   1500   1600    1700   1800 1900

0        10        20        30        40 х

^-Г" I -1

3.    Экспериментальные результаты

Эксперимент выполнен в вертикальной ячейке Хеле-Шоу, образованной двумя плоскопараллельными стеклами, разделёнными прокладкой, которая задаёт внутренние размеры полости — 9,0 см х 2,4 см х 0,12см. В стенках кюветы вдоль её средней плоскости были прорезаны неглубокие горизонтальные канавки, в которые входила заслонка, разграничивающая исходные реагенты. В качестве реагирующих жидкостей брались водные растворы азотной кислоты (верхний слой) и гидроксида натрия (нижний слой) в эквимолярной концентрации. Для запуска реакции заслонка убиралась из полости ячейки, и жидкости соприкасались, формируя горизонтальный фронт реакции.

Для комплексного изучения процессов, сопровождающих реакцию, одновременно использовалось несколько экспериментальных методик. Так, интерферометр Физо, собранный по автоколлимационной схеме, визуализировал распределение показателя преломления, обусловленное вариацией концентрации веществ, участвующих в реакции, и выделением тепла вследствие экзотермического характера реакции. Максимальное изменение температуры, измеренное термопарным зондом вблизи фронта реакции, не превышало 1 К, что позволило утверждать, что получаемые интерферограммы представляют собой поле показателя преломления, в целом отражающее распределение общей плотности смеси в ситуации, близкой к изотермической. Добавление в растворы реагентов светорассеивающих частиц и применение светового ножа позволяло выявлять структуру возникающего конвективного движения. Пространственное распределение реагентов и продукта реакции контролировалось с помощью индикаторов p H уровня.

Рисунок 6 иллюстрирует эволюцию реакции нейтрализации в выбранной системе жидкостей. В частности, сразу после соприкосновения между ними образуется переходная зона (Рис. 6 а-в, t_э = 300 с), внутри которой располагается фронт реакции. Сама переходная зона остается неподвижной, а перенос реагентов и продукта реакции в ней осуществляется за счёт диффузии. Со временем в области непосредственно над переходной зоной, формируется тонкий слой с низкой концентрацией кислоты, выгорающей в ходе реакции, что приводит к созданию неустойчивой стратификации плотности в нижней части верхнего слоя. Как следствие, во всём верхнем слое зарождается слабое конвективное движение.

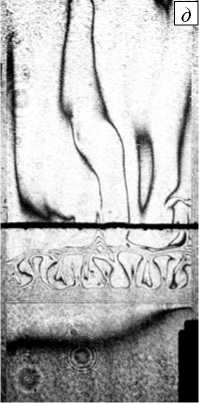
Через несколько минут после начала опыта внутри переходной зоны также развивается конвективное движение, но уже в виде горизонтального ряда конвективных ячеек (Рис. 6 г-е, t_э = 1100 с). Данная конвективная структура существует между двумя неподвижными участками переходной зоны, что указывает на формирование локализованного плотностного кармана с неустойчивым распределением плотности. Наблюдения за распределением уровня p H показывают, что внутри слоёв он остается однородным, в то время как в области ячеек имеет место сложное распределение данной величины: восходящие потоки насыщены продуктом реакции, формирующимся на фронте реакции. Напротив, нисходящие потоки обогащены кислотой, захватываемой конвективным движением из верхней части переходной зоны. Накопление продукта реакции происходит преимущественно в области, занятой ячейками. Обнаруженная структура существует в течение нескольких часов. Со временем ячейки, оставаясь внутри переходной зоны, увеличиваются в размерах, но уменьшается их число (Рис. 6 ж–и , t ₃ = 2250 с). Вертикальный размер переходной зоны также растет со временем благодаря диффузии.

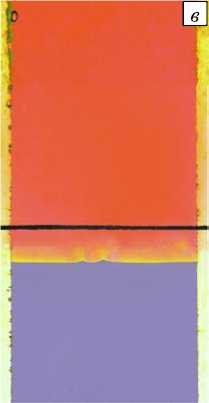
Рис. 6. Визуализация структуры течения (картинки слева), распределений концентрации (по центру), и p H-уровня (справа) для трёх моментов времени t _э от начала опыта, с: 300 ( а–в ), 1100 ( г – е ), 2500 ( ж – и )

1  ,   ,5,10

Рис. 6. Продолжение

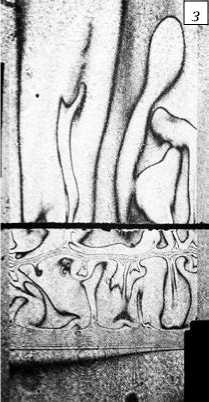
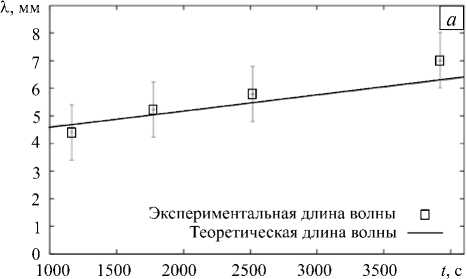
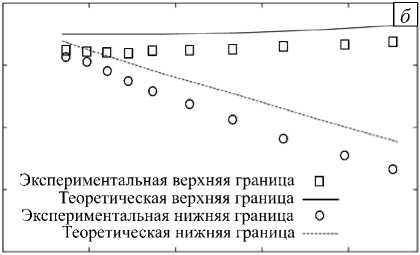
Рис. 7. Эволюция длины волны ( а ) и границ ( б ) хемоструктуры, полученная экспериментально (маркеры) и теоретически (линии)

О 500       1000       1500      2000 t, с

Отметим, что результаты эксперимента и теоретического расчёта хорошо согласуются друг с другом как по длине волны неустойчивости концентрационно-зависимой диффузии (Рис. 7 а ), так и по динамике расширения локальной конвективной зоны (Рис. 7 б ).

4.    Обсуждение и заключение

Данная работа содержит, по крайней мере, два совершенно новых результата.

Впервые обнаружен эффект возникновения хемоконвекции, локализованной в толще неподвижной жидкости. Внешне похожая структура наблюдалась экспериментально в работе [8], однако там исследовалась система двух несмешивающихся реагирующих жидкостей с чёткой границей раздела между ними. Как было показано в ряде теоретических работ [7, 9, 11], межфазная поверхность играет здесь важную роль в расположении ячеек. В настоящей работе выравнивание ячеек происходит из-за формирования локального плотностного кармана, в котором и развивается конвекция. За пределами этой области все конвективные возмущения затухают. В классических задачах конвекции, когда неоднородность плотности среды задаётся посредством манипулирования граничными условиями или внешними воздействиями (неоднородным нагревом, потоком вещества, внешним силовым полем и подобным), локальное существование конвекции в принципе невозможно, так как неоднородность формируется во всём пространстве, занятом жидкостью. Локализация конвективного движения внутри плотностного кармана становится возможной, только если вызывающая его причина — изменение плотности — тоже локальна. Химическая реакция идеально подходит на эту роль, поскольку фронт реакции, вблизи которого концентрация веществ и плотность среды резко меняются, — это понятие всегда локальное. Простым смешением веществ, без их реакции, по-видимому, сформировать локальный карман плотности невозможно, потому что диффузия изначально создаёт нелокальный массоперенос вещества до полного выравнивания концентрации. Возможно поэтому классические виды конвекции двойной диффузии (DD, DDD, DLC [15, 16]) в условиях гравитации также всегда приводят к нелокальному типу движения жидкости.

Второе достижение данной работы заключается в обнаружении нового типа неустойчивости — CDD — в семействе конвекции двойной диффузии. В данной работе показано, что движение жидкости в первоначально двухкомпонентной системе возникает благодаря зависимости коэффициентов диффузии реагентов и продукта реакции от их концентраций. Механизм неустойчивости сжато можно описать следующим образом. Ввиду того, что коэффициент диффузии образующейся в ходе реакции соли с ростом её концентрации существенно понижается, вблизи фронта происходит накопление продукта реакции. Реакция в объёме при этом не прекращается, но немного замедляется из-за того, что коэффициент диффузии кислоты с уменьшением её концентрации понижается. Оба эти факта служат причиной формирования вблизи фронта реакции условий для локального развития конвективного движения. Как оказалось, в механике жидкости данный физический механизм обсуждается впервые. Дело в том, что при рассмотрении конвекции в системах концентрированных растворов изменения концентрации веществ проявляют себя слабо вследствие того, что диффузия быстро выравнивает их по пространству. В полной мере эффект может сказаться лишь в условиях химической реакции, где вблизи фронта имеют место сильные перепады концентраций реагентов. А поскольку хемоконвекция — сравнительно новое направление в механике жидкости, то описываемые явления не сразу привлекли внимание исследователей.

Оба результата, хотя и связаны друг с другом, не являются тождественными. Численные эксперименты показали, что плотностный карман может формироваться в ходе реакции и без вариаций коэффициента диффузии реагентов. Таким образом, оба эффекта требуют своего дальнейшего независимого исследования.

Работа выполнена при финансовой поддержке РФФИ (проекты № 13-01-00508-a, 14-01-96021-р_урал_а) и Министерства образования и науки Пермского края (соглашение № С-26/004.4).