Конвективные режимы псевдопластической жидкости в квадратной полости при воздействии высокочастотных вибраций в условиях пониженной гравитации

Тепломассоперенос в неньютоновских жидкостях имеет практическое значение, например, для определения режимов работы центробежных насосов [1] . Неньютоновские свойства проявляют суспензии концентрированных твердых частиц, возникающие при разрыве пласта [2] . Из многообразия неньютоновских жидкостей выделяют класс обобщенных ньютоновских жидкостей [3] , при движении которых вязкие напряжения являются однозначной функцией скорости сдвига. Для описания обобщенных ньютоновских жидкостей, в зависимости от их реологии и условий движения, применяются различные реологические модели: Шведова–Бингама [4, 5] , Уильямсона [6] , Освальда-де Виля [7 –9] , Гершеля–Балкли [10] .

В ранних работах, касающихся конвекции неньютоновских жидкостей, рассматривалась только свободная конвекция и принималась в расчет нелинейная вязкость среды. Впервые задача одномерного стационарного конвективного течения вязкопластической жидкости Шведова–Бингама между двумя вертикальными параллельными пластинами, имеющими разную температуру, исследована в работе [11] , где получена зависимость безразмерного напряжения сдвига от набора чисел Gr и Pr без объединения в комплекс — число Релея Ra = Gr · Pr. Это сделано для более наглядного разделения подъемного механизма генерации течения (Gr) и тепломассопереноса в пограничном слое (Pr). Показано что при Gr • Pr < Gr • Pr c , где Pr c — критическое значение числа Прандтля, течение отсутствует, а при Gr • Pr > Gr • Pr c наблюдается стационарное течение с восходящим потоком вблизи горячей пластины и нисходящим потоком вблизи холодной. Кроме того, построена линейная зависимость безразмерного напряжения сдвига от набора чисел Gr и Pr . Аналогичная ситуация имеет место и при подогреве конечной области снизу в [12] , где приведены расчетные зависимости числа Нуссельта от числа Релея. В [13] рассмотрен тепломассоперенос в описываемой степенной моделью Освальда-де Виля жидкости, заключенной между вертикальными плоскостями с заданным перепадом температуры. Тепловой поток

охарактеризован числом Нуссельта Nu, для которого получено соотношение Nu = C (Gr ^ Pr n ) ^1/(3n+2 ) ; здесь n — показатель степени неньютоновости, C — постоянная, значение которой устанавливается путем расчетов. В работе [14] численно исследовалось движение жидкости Освальда-де Виля в широких диапазонах чисел Прандтля Pr ∈ [5,..., 12500] и показателя неньютоновости n ∈ [0.4,..., 1.0]. Выявлено, что для жидкостей с числом Прандтля Pr < 10 ³ показатель неньютоновости n является основным определяющим реологическим параметром, но и свободная поверхность, и малые скорости сдвига существенно влияют на профили скоростей во внешней части пограничного слоя и мало сказываются на локальном теплообмене. В [15, 16] рассмотрены двумерные стационарные режимы тепловой конвекции в полостях прямоугольного сечения с разными отношениями сторон. Полости полностью заполнены жидкостью Бингама и нагреваются сбоку. Расчеты проводились с помощью коммерческого пакета ANSYS Fluent с использованием двухвязкостной модели. Вычислены числа Нуссельта в зависимости от числа Бингама Bh = T 0 L ² / (pvx) для разных отношений сторон, где х — температуропроводность.

Вязкость неньютоновской жидкости является функцией не только скорости сдвига, но и температуры; важность этого факта показана в [5] . В [17] установлено, что в вязкопластической жидкости при превышении некоторой критической температуры возможна реализация нескольких стационарных конвективных режимов. Найдены значения управляющих параметров, определяющих границы между режимами. При T > T c вязкие напряжения сдвига, обусловленные подъемной силой, превышают предельное напряжение сдвига; в этом случае вязкопластическая жидкость фактически становится ньютоновской.

Нелинейная вязкость в вязкопластических жидкостях приводит к появлению в сдвиговом течении квазитвердых или жестких зон, то есть областей с подавленным сдвиговым течением жидкости. В [6] прослежена эволюция формы квазитвердой зоны с увеличением числа Релея: кольцевая зона трансформируется в крестообразную и в дальнейшем распадается на ряд более мелких зон. Аналогичное исследование для замкнутой полости прямоугольного сечения выполнено в [18] . Прямое численное моделирование при больших числах Релея и Бингама, проведенное Виханским [19, 20] для полости квадратного сечения, подогреваемой снизу, позволило вычислить критические значения предельного напряжения сдвига для широкого диапазона аспектных соотношений для полости L _x /L _y ∈ [0 . 5 ,..., 7 . 0] . Выяснена форма квазитвердых зон, в которых напряжения сдвига меньше предела текучести. В работах [21, 22] изучены механизмы неустойчивости в слоях неньютоновской жидкости различной пространственной ориентации. Показано, что при малых значениях числа Прандтля неустойчивость обусловлена монотонными гидродинамическими возмущениями, а при числах Прандтля, превышающих некоторое значение, — тепловыми волнами. Пороговое значение числа Прандтля, при котором происходит смена механизма неустойчивости, уменьшается с ростом вязкости при малых скоростях сдвига.

Условия квазиравновесного и жесткого состояний обобщенных ньютоновских жидкостей в невесомости описаны в [21] . Продемонстрировано, что жесткое состояние таких жидкостей в наклонном слое возможно в невесомости или при одновременном совпадении направлений вибрации, гравитационного поля и градиента температуры. В невесомости жесткое состояние абсолютно устойчиво.

В статье [23] на основании уравнений термовибрационной конвекции для случая невесомости решена линейная задача устойчивости квазиравновесия бесконечного слоя жидкости Уильямсона относительно малых периодических вдоль слоя возмущений. Численные исследования проводились при разных углах наклона оси вибраций к слою. Показано, что наиболее опасными являются гидродинамические монотонные возмущения. Усиление вязкопластических свойств жидкости приводит к дестабилизации основного состояния при всех углах наклона оси вибраций. Увеличение числа Прандтля стабилизирует квазиравновесное состояние псевдопластической жидкости.

В статьях [8, 9] рассмотрена устойчивость конвективного течения неньютоновской жидкости в вертикальном слое на примере степенной трехпараметрической реологической модели, где, в отличие от классической степенной модели Освальда-де Виля, используется дополнительный регуляризационный параметр — динамическая вязкость при нулевой скорости сдвига. Получено, что усиление псевдопластических свойств жидкостей оказывает дестабилизирующее действие на течение, а усиление дилатантных свойств, наоборот, стабилизирует его.

Имеются публикации, в которых анализируются результаты применения различных реологических моделей к аналогичным системам. Так, в [24] установлено, что структуры квазитвердых зон, рассчитанные с использованием модели Гершеля–Балкли при числах Релея, незначительно превышающих пороговые значения, близки к таковым, рассчитанным с использованием модели Шведова–Бингама в [6]. В цикле работ Матвиенко О.В. и Литвиновой А.Е. [25–27] с помощью реологических моделей изучены установившиеся течения сред. Исследовались течения закрученных потоков в цилиндрическом канале псеводпластической [25], дилатантной [26] и термовязкой [27] жидкостей. Псевдопластическая и дилатантая жидкости описывались реологической моделью Гершеля-Балкли, термовязкая жидкость — моделью Сиско. Показано, что при низких значениях перепада давления псевдопластические свойства среды приводят к значительному гидравлическому сопротивлению. С увеличением перепада давления гидравлическое сопротивление потока уменьшается, что связано с разрушением внутренней структуры среды, определяющей псевдопластические свойства.

В [28] рассматриваются модели вязкости (простейшая алгебраическая модель Берковера и Инглемана и модель Папанастасиоу) применительно к течениям псевдопластической жидкости (n = 0.6) в полости квадратного сечения на основе двухполевого метода. В результате численного моделирования и сравнения результатов исследования с данными других авторов оптимальной признана модель Берковера и Инглемана, в которой эффективная вязкость ^ ef f задается соотношением faff = / // (A) ² +е ² j , где A — интенсивность скорости деформации, ε — параметр регуляризации (ε = 0.01).

Особый интерес представляют работы, в которых получены аналитические решения при рассмотрении неньютоновских жидкостей. Так, в [6] впервые в рамках реологической модели Уильямсона выведено аналитическое выражение, связывающее пороговое значение числа Релея, при котором возникает конвекция линейно-вязкопластической жидкости Бингама, и предельное напряжение сдвига, а в [18] сформулированы два вариационных принципа для определения пороговых значений числа Релея и формы квазитвердых зон при возникновении конвекции в вязкопластической жидкости Бингама в вертикальной полости прямоугольного сечения с разным соотношением сторон.

В [29] приводятся результаты численного моделирования естественного конвективного теплообмена между вертикальной изотермической поверхностью и псевдопластической или дилатантной жидкостями. Демонстрируется зависимость числа Нуссельта, характеризующего интенсивность теплообмена, от скорости сдвига.

Известно, что вибрации являются одним из механизмов генерации конвективного течения. В области малых и умеренных частот вибрационный механизм возникновения свободной конвекции связан с наложением поля вибрационного ускорения aω ² на гравитационное поле g, что приводит к модуляции подъемной силы. При высокочастотных вибрациях, когда времена пульсаций много меньше характерных вязких времен, осреднение уравнений движения жидкости приводит к появлению в них массовой осредненной вибрационной силы. Таким образом, вибрации являются независимым механизмом генерации конвекции, то есть могут порождать конвективное течение даже в отсутствие поля силы тяжести [30] .

Моделирование структур течений и исследование устойчивости вторичных колебательных режимов при вертикальных вибрациях нагреваемой снизу полости с ньютоновской жидкостью проведено в работе [31] . Расчеты выполнены для трех значений числа Pr: 0.02, 1, 15. Показано, что высокочастотные вертикальные вибрации оказывают различное влияние на устойчивость конвективных течений: относительно слабые стабилизируют их, увеличение же вибрационного числа Релея приводит к снижению порога устойчивости вплоть до полной дестабилизации. Аналогичная система рассмотрена в статье [32] для значений числа Релея Ra: 1, 10 ⁴ , 10 ⁶ , при безразмерной частоте вибраций в пределах 1, . . . , 10 ⁴ . Установлено, что при малых Ra доминирует вибрационный механизм генерации течения; вибрационное движение значительно увеличивает скорость теплопереноса. При Ra = 10 ⁶ преобладает гравитационный механизм, а вибрации не способствуют значительному усилению теплопереноса.

В работе [33] представлены экспериментальные результаты в земных условиях и на борту станции «Мир», полученные с помощью прибора ДАКОН, который предназначен для изучения конвекции, вызванной низкочастотными микроускорениями. Приведено большое количество результатов натурных экспериментов, которые могут быть полезными для верификации математических моделей.

В [34] исследуется влияние вибраций с различными углами наклона вибрационного ускорения и силы тяжести в полости и слое. Построены карты устойчивости режимов конвективных течений ньютоновской жидкости на плоскости Pr · Gr - Pr · Gv.

В работе [35] экспериментально и теоретически рассмотрено влияние высокочастотных горизонтальных вибраций на вертикальную конвекцию ньютоновской жидкости в ячейке Хеле-Шоу, нагреваемой снизу и расположенной в однородном поле силы тяжести. В качестве рабочей жидкости использовалось трансформаторное масло. Время стабилизации конкретного конвективного режима оценивалось по характерным временам релаксации температурных и гидродинамических возмущений и составило около 1.5 ч; время выхода на устойчивый режим в эксперименте составило более 2 ч. Показано, что горизонтальные вибрации снижают порог квазиравновесной устойчивости. Определены области существования устойчивых и неустойчивых режимов вибрационной конвекции. Найдены новые устойчивые автоколебательные режимы, которые названы вибрационными потоками.

Еще одно экспериментальное исследование термовибрационной конвекции ньютоновской жидкости в условиях пониженной гравитации проведено в работе [36]. Изучено температурное поле в разных плоскостях. Обнаружено, что значительный перенос тепла имеет место при вибрациях в условиях низкой гравитации, тогда как в отсутствие вибраций он слабее, а при нормальной гравитации пренебрежимо мал, что совпадает с выводами из [37].

Экспериментальному и теоретическому изучению термовибрационной конвекции в условиях пониженной гравитации посвящена статья [38] . Показано, что увеличение переноса тепла связано с усредненным течением, интенсивность которого пропорциональна вибрационному ускорению. Результаты трехмерного прямого численного моделирования и двумерного численного моделирования, основанного на осредненных уравнениях термовибрационной конвекции, хорошо согласуются с экспериментальными данными.

Приближенное аналитическое выражение поля скорости в слое жидкости Уильямсона, помещенном между двумя осциллирующими плоскостями, получено в [39] . Решение, записанное для случая ламинарного течения, учитывает параметры жидкости Уильямсона, толщину слоя, перепад давления, температуру, частоту вибраций и может использоваться для верификации вычислительных алгоритмов.

В работе [40] рассмотрено влияние гравитационных, тепловых, вибрационных и магнитных полей на движение тонкого слоя псевдопластической жидкости Уильямсона со свободной поверхностью по вибрирующей наклонной плоскости, помещенной в магнитное поле. Авторы наблюдали сначала синхронные колебания пленки вместе с вибрирующим основанием, затем — нарастание колебаний на свободной поверхности.

В [41] аналитически решена двумерная задача установившегося течения в слое наножидкости, помещенной на растягиваемую с заданной скоростью u ₀ подложку, нормальную к магнитному полю. Жидкость представляет собой взвесь подвижных магнитных наночастиц и описывается реологической моделью Уильямсона. Решения учитывают энергию активации и диффузию наночастиц в температурном и магнитном полях, а также их конвективный перенос. Выявлено, что большие значения параметра А = 3Г (2u3/v ) 1/2 , где Г — константа модели Уильямсона, снижают коэффициент поверхностного трения, тогда как рост магнитного параметра M = 3аВ 0 /ри ₀ влияет противоположно (здесь а — электропроводность, B0 — индукция магнитного поля).

Изучению термовибрационной конвекции неньтоновских жидкостей в замкнутых полостях посвящены работы [42 –44] . В [42] изучена термовибрационная конвекция псевдопластической жидкости в замкнутой прямоугольной полости, которая в невесомости совершает продольные высокочастотные линейно-поляризованные вибрации; градиент температуры перпендикулярен направлению вибраций. Величина вибрационного воздействия на жидкость определялась вибрационным числом Грасгофа Gv. Показано, что с его ростом в псевдопластической жидкости 4-вихревое термовибрационное течение сначала трансформируется в 3-вихревое, а затем в 5-вихревое. Причем 5-вихревое течение может иметь колебательный характер при определенной комбинации Gv и параметра неньютоновости.

В работах [43, 44] выполнено систематическое изучение эволюции осредненных конвективных режимов. Причем в этой задаче впервые четко разделены управляющие параметры. Термовибрационный механизм генерации конвективного течения описан обычным числом Грасгофа, а для характеристики интенсивности вибрационного механизма введен специальный вибрационный параметр V . Для широкого диапазона управляющих параметров на плоскости Gr — V построена карта конвективных режимов. Очерчены границы устойчивости стационарной осредненной конвекции. Показано, что после потери устойчивости стационарным осредненным течением в полости возможна реализация двух колебательных осредненных конвективных режимов, обладающих разной симметрией.

Из приведенного обзора литературных источников следует, что вопросы влияния вибраций на структуру течений, режимы переноса тепловой энергии и границы областей реализации колебательных режимов в нелинейно-вязких средах остаются недостаточно изученными. Целью настоящей работы является исследование влияния высокочастотных вертикальных вибраций на конвективные режимы псевдопластической жидкости в полости квадратного сечения в условиях пониженной гравитации.

• 2.    Постановка задачи: основные уравнения, параметры и граничные условия

Рассматривается полость с квадратной проекцией на координатную плоскость (x, y) с твердыми идеально теплопроводными границами, заполненная псевдопластической жидкостью. Полость находится в условиях пониженной гравитации и совершает вертикальные линейно-поляризованные высокочастотные вибрации малой амплитуды вверх-вниз в направлении единичного вектора n . Начало координат находится на нижней стенке полости. Геометрия задачи, направление осей и положение начала координат показаны на рисунке 1; вдоль оси z полость полагается бесконечной. Единичный вектор γ направлен вертикально вверх против направления силы тяжести. В полости на вертикальных границах x = ±h заданы постоянные разные температуры ± 0, на горизонтальных границах температура меняется по линейному закону T = 0x/ h. На всех границах выполняется условие прилипания. Жидкость считается несжимаемой.

Рис. 1. Геометрия задачи

Для описания поведения псевдопластической жидкости использовалась реологическая модель Уильямсона [6] :

A                     du i   du j         1

Tij = \ B+^ + ^) eij, eij = vdxj+dX“y, I2 = 2 eij eji, где A, B — реологические параметры модели Уильямсона, I2 — второй инвариант тензора скорости сдвига, µ∞ — динамическая вязкость при бесконечно больших скоростях сдвига. Необходимо отметить, что в предельном случае, когда A = 0, реологическая модель Уильямсона трансформируется в реологическую модель ньютоновской жидкости. В случае конечных A и B ^ 0 (A > Б) модель Уильямсона описывает вязкопластические среды.

Высокочастотные вибрации полости с жидкостью в неоднородном поле температуры вызывают вибрационноконвективные течения, для описания которых все физические поля удобно разделить на осредненную и пульсационную компоненты. Когда период колебаний много меньше всех гидродинамических и тепловых времен, а амплитуда смещения в некотором смысле мала, путем осреднения можно получить замкнутую систему уравнений для осредненных и пульсационных полей. Уравнения термовибрационной конвекции для случая линейно-поляризованных вибраций полости с жидкостью имеют вид [30, 45] :

c ^U + ( u V ) u = —-V p +-div т + двТ Y + |(ашв ) 2 w V(T n — w ),

∂T

— + u V T = x^T, div u = 0, div w = 0, Vx w = VT x n . ∂t

Здесь u = (u _x ,u y ,u z ) — вектор скорости жидкости; T , p — температура и давление как функции медленного времени t , описывающие осредненное конвективное течение; a — амплитуда смещения; ω — циклическая частота вибраций; w = (w _x ,w y ,w _z ) — амплитуда пульсационной скорости; т — тензор вязких напряжений; x — коэффициент температуропроводности жидкости; β — коэффициент теплового расширения; ρ — плотность жидкости. Вид вязкого слагаемого div т определяется реологической моделью.

Уравнения (2) справедливы в случае, когда исследуемая жидкость полностью занимает замкнутую полость. Вибрации считаются высокочастотными, не акустическими, амплитуда полагается малой, то есть выполняются условия:

ш »

µ 0 χ ρh ^{2 ,} h ²

аве <  h,

х 2пс ,    .    ^0

A c = ~иГ ^ h h ^ рс,

где h — характерный размер полости, Θ — характерная разность температур, λc — длина звуковой волны, соответствующая частоте вибраций, c — скорость звука, ^ о = (A/B + ^ _№ ) — динамическая вязкость при бесконечно малом сдвиге.

Осредненная по быстрому времени — t - = ut, часть тензора вязких напряжений (1) имеет вид:

2 π

1A cTij = 2nJ Б+в + VI2 + ^“J ej dt-’

• I 2 (¹/^2)e Oij e O ji , e O ij ^auee wij Sint - + e uij ,

∂wi ∂wj            ∂ui  ∂uj ewij —      +      , euij —      +      •

∂x j    ∂x i              ∂x j   ∂x i

Компоненты скорости сдвига e ij разделяются на две части: e wij определяются амплитудой скорости пульсаций, а e _ui j — скоростью осредненного конвективного движения. Подробный вывод и границы применимости уравнений (2) и (3) приведены в [21, 45, 46] .

В настоящей работе уравнения термовибрационной конвекции (2) и (3) удобно переписать в терминах завихренности скорости fi = Vx u и функции тока осредненного (u x = d/ / dz, u _z = —дф /dx) и пульсационного ( w z = —дф/дх, w x = дф/dz) течений и исключить из уравнений (2) давление.

При обезразмеривании уравнений (2) и (3) в качестве характерных масштабов выбраны: для длины — h , для скорости осредненного течения — geV\\²p/ ^ ^ , для времени — Ь²рД _ю , для температуры и амплитуды пульсационной скорости — 0, для давления — ge@hp. Уравнения (2) и (4) в безразмерном виде в терминах ψ , ϕ и Ω выглядят так:

∂ ² ψ ∂ ² ψ

∂x ² ∂z ²

₊ д ² Ф

∂z ²

∂T ∂x ,

^ + Gr ^ ∂t ∂z∂x

дфдт   1 /д ²Т д²Т\

Gr—=      + хх dz Pr \ хх2 dz2 )

l^T wxx ^H w      , ^T wxz ^T wzx ^H w

∂x∂z

д ² ф \

∂x ^{2 ,}

H w = V- [ sint - dt - , Н и =1 [ dt - , ^{2 п} 00                    ^{2 п} 00

Н =1 +

ν

1+vBh\ 4 \ V Ф^ sint - + ∂x∂z

∂ ² ψ ∂ ²

∂z ² ∂x

.

Уравнения (4) следует дополнить граничными условиями в безразмерном виде:

х = ± 1: u = 0, w x = 0, Т = ± 1;     z = 0.2: u = 0, w z = 0, T = х.              (5)

Задача (4) , (5) характеризуется пятью безразмерными параметрами: числом Грасгофа Gr = дв0Ь 3 р ² /р ^ ; вибрационным параметром V = aau² /g (а = р ^ / ^р ph ² ) < 1); числом Прантля Pr = р ^ /(рх); реологическим параметром Bh = pge0h/A; параметром неньютоновости v = А/(Вр _те ). Безразмерный реологический параметр Bh, как и число Грасгофа Gr, характеризует конкуренцию гравитационного механизма генерации конвекции и диссипативного механизма, в данном случае связанного с нелинейной вязкостью жидкости. Причем Bh = PrGr/ст, где ст = h ² А/(р ^ х), согласно работам [6, 47] , — безразмерный динамический предел текучести. Параметр V определяет интенсивность вибрационного воздействия на жидкость, равняется отношению вибрационного ускорения к ускорению свободного падения и не зависит от конвективного параметра βΘ , связанного с равновесным градиентом температуры. Использование V позволяет четко отделить влияние вибрационного механизма генерации конвекции от теплового. Оценки показывают, что при заданных параметрах жидкости и геометрических параметрах полости, в условиях пониженной гравитации V >  1. Вибрационный параметр связан с классическим для задач о темовибрационной конвекции вибрационным числом Грасгофа Gv = (a^e^h/v ) ² соотношением: V = V Gv / Gr [43, 44] .

Динамический предел текучести ст, как и число Прандтля Pr, зависит от физических параметров жидкости. Для заданной псевдопластической жидкости эти параметры можно зафиксировать. В этом случае изменения Bh или Gr определяются только изменением характерного градиента температуры в полости.

Численные расчеты проводились методом конечных разностей. Пространственные производные аппроксимировались конечными разностями 2-го порядка точности. Интегрирование по времени выполнялось методом Эйлера по схеме 1-го порядка точности. Уравнения Пуассона для функций тока на каждой итерации решались методом последовательной верхней релаксации. Значения завихренности на границах вычислялись по формуле Тома: П| = 2(^| — ^|-1)/Ah2, где Ah — шаг пространственной сетки [48, 49]. При расчетах применялась равномерная пространственная сетка с шагом ∆h = 1/40. Шаг выбирался исходя из сходимости решения с уменьшением ∆h.

Основные расчеты выполнены для σ = 62.5, Pr = 10, V = 100 и значений ν : 25, 100, 500. Задача в аналогичной постановке, но без вибраций и в поле силы тяжести решена в [6] , значения параметра σ и числа Pr соответствуют этой работе. Термовибрационная конвекция псевдопластической жидкости Уильямсона для случая прямоугольной полости в условиях невесомости описана в [42] .

В результате вычислительных экспериментов в исследуемом диапазоне чисел Грасгофа для псевдопластических сред обнаружено, что существует два типа решений задачи, согласно которым наблюдаются различные конвективные структуры. Первый тип решений условно назван ньютоновской модой, поскольку реализуется в ньютоновской жидкости, то есть для ν = 0 (A = 0). С ростом числа Грасгофа для ньютоновской моды характерна потеря устойчивости осредненным стационарным конвективным течением и переход к осредненной колебательной конвекции [43, 44] . Второй тип решений — неньютоновская мода — существует только для ν > 0, то есть для псевдопластической жидкости. У этой моды переход к нестационарным режимам конвекции не наблюдается.

• 3.    Результаты вычислений

На рисунке 2 представлены зависимости числа Нуссельта Nu и максимума функции тока ψ max от числа Грасгофа Gr для псевдопластических жидкостей с параметрами неньютоновости ν : 0. 25, 100, 500. Число

Нуссельта определяет поперечный конвективный тепловой поток, приходящийся на единицу длины вертикальной

(в обсуждаемом случае — левой) границы полости: Nu=

dz. Значение Nu = 1 отвечает слабоинтенсивному

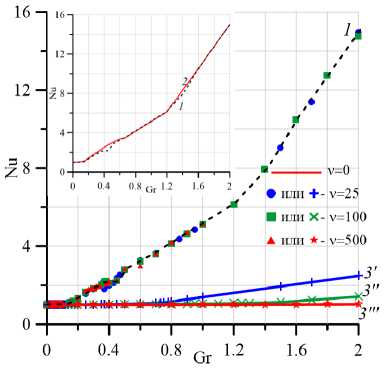
(ползущему) конвективному движению жидкости и отсутствию конвективного теплопереноса; имеет место теплопроводный механизм переноса тепла через полость. Изолинии поля температуры параллельны друг другу и вертикальным стенкам полости. При возникновении интенсивного конвективного движения к теплопроводному механизму переноса тепла добавляется конвективный, число Нуссельта становится большим 1, а изотермы искривляются. Для ньютоновской моды расчетные точки для всех четырех значений параметра неньютоновости ν очень близки и ложатся вдоль одной кривой. Обработка результатов расчетов для ν ̸ = 0 методом наименьших квадратов дает штриховую линию 1 . Сплошная линия 2 на врезках фрагментов ( а ) и ( б ) соответствует ньютоновской жидкости (ν = 0). Видно, что сплошная и пунктирная линии фактически накладываются друг на друга. Можно сделать вывод, что интенсивность течения псевдопластической жидкости в широком диапазоне чисел Грасгофа не зависит от параметра неньютоновости.

При ньютоновской моде для псевдопластической жидкости так же, как и для ньютоновской жидкости [43, 44] , имеет место переход от стационарного режима течения к колебательному. У псевдопластической жидкости он происходит в пределах плоского горизонтального участка кривой 1 . Здесь увеличение числа Gr

( a )

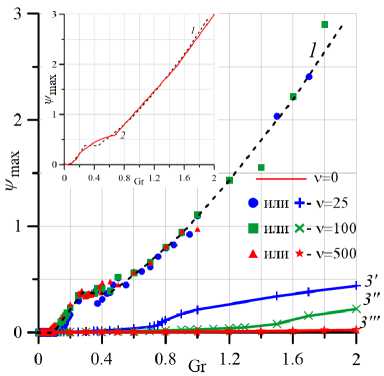
Рис. 2. Зависимости числа Нуссельта Nu ( а ) и максимума функции тока ψmax ( б ) от числа Грасгофа Gr : 1 - псевдопластическая жидкость, ньютоновская мода; 2 – ньютоновская жидкость, ν = 0 ; 3’ , 3 ”, 3 ”’ - псевдопластическая жидкость, неньютоновская мода

не приводит к росту интенсивности течения, так как тепловая энергия преобразуется в энергию колебаний. Переход к колебательному режиму для всех ν не сопровождается изменением структуры течения, а вызывает только пульсацию вихрей. Критические значения чисел Грасгофа Grc, при которых стационарное осредненное конвективное течение теряет свою устойчивость, в вычислительных экспериментах определялись из анализа структуры и зависимостей от времени числа Нуссельта и максимума функции тока осредненного течения. Структуры течений и указанные зависимости будут обсуждаться ниже. Значения Grc зависят от параметра неньютоновости и представлены в таблице 1.

Таблица 1. Критические числа Грасгофа при разных значениях параметра неньютоновости для ньютоновской моды

Номер расчета	1	2	3	4
ν	0	25	100	500
Gr c	0.67	0.37	0.38	0.27

Из таблицы 1 видно, что порог устойчивости стационарного осредненного конвективного течения псевдопластической жидкости ниже аналогичного порога для ньютоновской жидкости. Подробно зависимость Gr c от параметра ν не исследовалась, но можно предположить, что имеется достаточно широкий диапазон умеренных значений параметра неньютоновости, в котором критические числа Грасгофа близки между собой по величине. И только при больших ν значения Gr c будут уменьшаться.

Сценарий потери устойчивости стационарным осредненным конвективным течением в псевдопластической жидкости аналогичен сценарию для ньютоновской (ν = 0) жидкости [42, 43] . Критическому числу Грасгофа Gr _c = 0.67 в этом случае соответствует излом кривых 2 на врезках рисунка 2. Как отмечалось выше, этот излом для псевдопластической жидкости превращается в плато (см. там же кривые 1 ).

Второму типу решений (неньютоновской моде) задачи (4) , (5) для псевдопластической жидкости соответствуют кривые 3 на рисунке 2. Видно, что для всех трех ненулевых значений параметра неньютоновости расчетные точки ложатся вдоль разных кривых. С увеличением числа Грасгофа интенсивность течения растет и меняется его структура. Эволюция течений для неньютоновской моды будет подробно рассмотрена ниже. Для данной моды характерно менее интенсивное, по сравнению с ньютоновской модой, течение. Перехода к нестационарным режимам в области апробированных чисел Грасгофа (0 ⩽ Gr ⩽ 5) не наблюдается. Как и в случае ньютоновской моды, с ростом параметра неньютоновости ν интенсивность течения снижается.

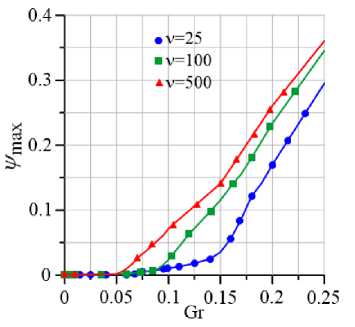
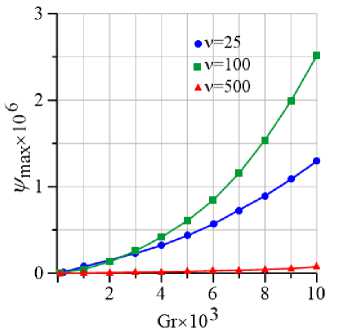
На рисунке 3а представлены зависимости максимума функции тока от числа Грасгофа для ньютоновской моды течения псевдопластической жидкости при значениях 0 ⩽ Gr ⩽ 0.25 (см. Рис. 3а ). При Gr ≈ 0.05 для всех ν наблюдается достаточно резкое увеличение интенсивности течения (линии отрываются от оси абсцисс). При увеличении параметра неньютоновости ν растет эффективная вязкость жидкости, что приводит к снижению интенсивности течения. Более наглядно это видно на рисунке 3 б , где интенсивность течения резко падает с увеличением ν. Усиление нелинейно-вязких свойств, когда ν → ∞ , в рамках реологической модели Уильямсона приводит к тому, что жидкость приобретает вязкопластические свойства. Для вязкопластической жидкости существуют значения чисел Gr или Bh, меньше которых в жидкости не наблюдаются сдвиговые течения, то есть она находится в квазитвердом (жестком) состоянии.

( a )

( б )

Рис. 3. Зависимость максимума функции тока от числа Грасгофа для ньютоновской моды псевдопластической жидкости при различных параметрах неньютоновости для 0 ⩽ Gr ⩽ 0.25

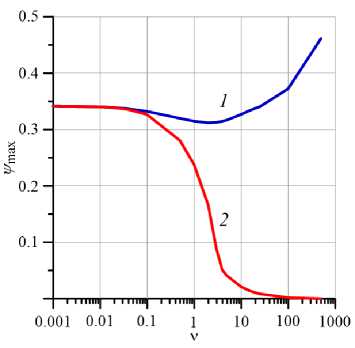
На рисунке 4 представлены зависимости числа Нуссельта Nu и максимума функции тока осредненного течения ψmax от значения параметра неньютоновости ν для ньютоновской (кривые 1) и неньютоновской (кривые 2) мод решений задачи (4), (5). Кривые построены для вибрационного параметра V = 100 и числа Грасгофа Gr = 0.3. Из рисунка видно, что при ν → 0 кривые 2, соответствующие неньютоновской моде, приближаются к кривым 1. Расчеты показали, что при ν ⩽ 0.05 фактически реализуется решение только первого типа, которое характерно для ньютоновской жидкости [43, 44]. С другой стороны, с увеличением ν значения Nu и ψmax для ньютоновской моды (кривые 1) после прохождения точки локального минимума имеют тенденцию к росту, тогда как для неньютоновской моды наблюдается монотонное снижение интенсивности течения при увеличении ν (см. кривые 2). При ν → ∞, то есть при переходе к вязкопластическому пределу, когда эффективная вязкость жидкости линейно зависит от скорости сдвига, неньютоновская мода фактически исчезает.

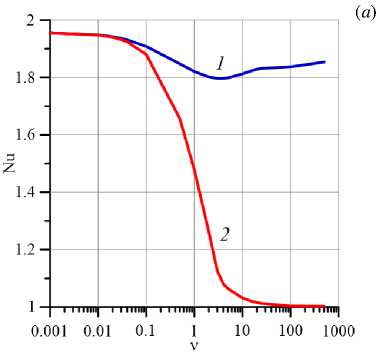
Рис. 4. Зависимость числа Нуссельта Nu ( а ) и максимума функции тока осредненного течения ψmax ( б ) от параметра неньютоновости ν для ньютоновской (кривые 1 ) и неньютоновской ( 2 ) мод для числа Грасгофа Gr = 0.3 и вибрационного параметра V = 100

• 4.    Конвективные структуры

  • 4.1.    Ньютоновская мода

Выше показано, что интенсивность течения, характеризуемая числом Nu и максимумом функции тока осредненного течения ψ max , для случая ньютоновской моды не зависит от параметра неньютоновости. Расчеты выявили, что характер эволюции конвективных течений и их структуры для этой моды при различных значениях ν хотя и имеют некоторые отличия, но в целом очень похожи. Ниже приведены характеристики эволюция конвективных течений для решения первого типа (ньютоновской моды) задачи (4) , (5) при изменении числа Грасгофа в зависимости от параметра неньютоновости.

На рисунке 5 представлены характерные структуры осредненного стационарного течения: поля функции тока осредненного течения (ψ), функции тока пульсационного течения (ϕ), температуры (T) и завихренности осредненного течения (Ω) в зависимости от числа Грасгофа в случае ньютоновской моды. Все поля построены для параметра неньютоновости ν = 25.

При малых значениях числа Грасгофа Gr ⩽ 0.002 в полости реализуется медленное одновихревое стационарное конвективное течение, характерный вид функции тока ψ которого для Gr = 0.001 показан в первой колонке рисунка 5. При этом число Нуссельта близко к единице (см. Рис. 2а ), что свойственно для ползущего конвективного течения, в котором преобладает теплопроводный механизм переноса тепла через полость. Изолинии поля температуры T параллельны вертикальным стенкам полости при Gr = 0.001.

С увеличением числа Грасгофа 0.002 < Gr < 0.04 ползущее одновихревое конвективное течение изменяет свою форму: осредненный вихрь наклоняется и вытягивается вдоль диагонали полости, в застойных зонах, которые расположены в углах полости, сначала появляются два дополнительных вихря малой интенсивности, затем течение трансформируется в 3-вихревое (для Gr = 0.003). Дальнейшее увеличение числа Gr приводит к усилению интенсивности угловых вихрей и деформации центрального вихря в осредненном стационарном течении — основной вихрь разделяется на два, удаляющиеся друг от друга. Поля развитого 3-вихревого стационарного

Gr=0.001         Gr=0.003         Gr=0.02          Gr=0.06           Gi=0.3

Рис. 5. Изолинии функции тока осредненного течения (ψ), функции тока пульсационного течения (ϕ), температуры (T) и завихренности осредненного течения (Ω) для параметра неньютоновости ν = 25 в случае ньютоновской моды при различных значениях числа Gr течения соотносятся с Gr = 0.02.

При числах Грасгофа 0.04 ⩽ Gr < 0.1 в полости реализуется 4-вихревое конвективное течение, которое характерно для терморвибрационной конвекции в невесомости [30, 42, 43] . Структуры полей функций тока ψ и ϕ, температуры T и завихренности Ω представлены на рисунке 5 при Gr = 0.06. При Gr > 0.05 значения Nu и ψ _max отклоняются от оси абсцисс (см. Рис. 2) , что свидетельствует об интенсификации конвективного течения и возникновении существенного конвективного переноса тепла через полость.

При дальнейшем увеличении числа Грасгофа (0.1 ⩽ Gr < 0.37) 4-вихревое течение вновь трансформируется в 3-вихревое, обусловленное совместным влиянием вибрационного и гравитационного механизмов генерации конвекции. При Gr > 0.1 изотермы заметно искривляются (см. поле температуры при Gr = 0.3), что свидетельствует о преобладании конвективного механизма переноса тепла.

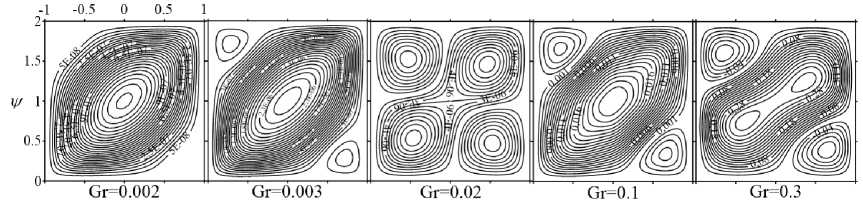
Рис. 6. Изолинии осредненной функции тока для параметра неньютоновости ν = 100 в случае ньютоновской моды при различных значениях числа Gr

Характерные структуры полей функции тока осредненного стационарного конвективного течения псевдопластической жидкости при различных числах Грасгофа для ν = 100 в случае ньютоновской моды, показаны на рисунке 6. При малых числах Грасгофа Gr ⩽ 0.002 в полости реализуется медленное одновихревое течение, которое при увеличении числа Грасгофа трансформируется в 3-вихревое. При этом течении центральный вихрь наклоняется и вытягивается вдоль диагонали полости, а в застойных зонах, расположенных в углах полости, возникают дополнительные вихри малой интенсивности (см. фрагмент при Gr = 0.003). Увеличение Gr приводит к тому, что у центрального вихря появляются два центра, и течение становится похожим на термовибрационное 4-вихревое (см. фрагмент при Gr = 0.02). Такая структура существует в области чисел Грасгофа 0.009 < Gr < 0.05. С дальнейшим ростом Gr сначала сливаются центры основного вихря (см. Gr = 0.1), а затем появляется два центра (см. Gr = 0.3). Дополнительные вихри в углах полости меняют свою интенсивность с изменением Gr. Показанное на фрагментах Gr = 0.1 и Gr = 0.3 течение с 3-мя вихрями, характерно для равноправного влияния гравитационного и вибрационного механизмов генерации конвекции. Изолинии функции тока пульсационного течения, изолинии поля температуры и завихренности осредненного течения имеют качественный вид, аналогичный показанному на рисунке 5 для ν = 25.

Структура конвективных течений, возникающих в полости при ν = 500, показана на рисунке 7. При малых числах Грасгофа (Gr ⩽ 0.002) в полости имеет место очень медленное ползущее конвективное движение жидкости, напоминающее движение вязкопластических сред [6, 47] . В центре полости образуется вращающееся ядро, в котором практически отсутствуют сдвиговые течения. При увеличении числа Грасгофа интенсивность центрального вихря нарастает, в застойных зонах появляются угловые вихри малой интенсивности. Для случая ν = 500 существует два диапазона чисел Грасгофа, при которых реализуется 3-вихревая структура осредненного конвективного течения. В первом диапазоне 0.002 < Gr ⩽ 0.05 3-вихревое течение по мере увеличения числа Грасгофа сначала трасформируется в структуру, похожую на 4-вихревое конвективное течение (см. Gr = 0.02), что говорит о преобладании вибрационного механизма генерации конвекции. Затем вихри в углах полости затухают и для 0.06 ⩽ Gr < 0.15 в полости вновь наблюдается одновихревое течение (см. Gr = 0.1) с наклонным центральным вихрем и застойными зонами по углам. Второму интервалу чисел Грасгофа 0.15 ⩽ Gr < 0.27, с которым соотносится 3-вихревое течение, отвечают структуры, показанные на фрагментах Gr = 0.15 и 0.26 и свидетельствующие о совместном влиянии гравитационного и вибрационного механизмов генерации конвекции. Поля функции тока пульсационного течения, поля температуры и завихренности осредненного течения имеют вид, аналогичный представленному на рисунке 5.

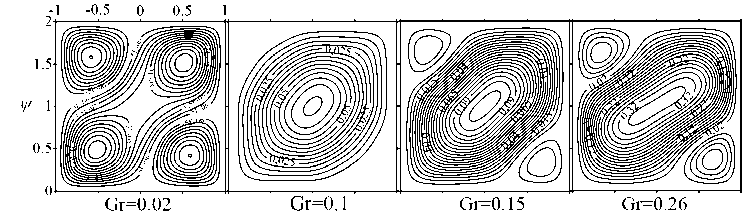
Рис. 7. Изолинии осредненной функции тока для параметра неньютоновости ν = 500 в случае ньютоновской моды при различных значениях числа Gr

Для значений параметра неньютоновости ν = 100 и ν = 500 отсутствуют области чисел Грасгофа, с которыми соотносится чистое 4-вихревое течение. По всей вероятности, в условиях пониженной гравитации усиление неньютоновских свойств жидкости (увеличение параметра ν) подавляет 4-вихревое течение, характерное для термовибрационной конвекции ньютоновской жидкости.

Когда число Грасгофа для различных ν в решении задачи (4) , (5) вида ньютоновской моды достигает критического значения (см. Табл. 1) , стационарное конвективное течение теряет устойчивость, и в полости возникают осредненные колебательные конвективные режимы. Важно, что при всех исследованных значениях параметра неньютоновости вблизи порога устойчивости в полости реализуются одинаковые по структуре и близкие по интенсивности 3-вихревые осредненные стационарные конвективные течения. После потери устойчивости сценарии эволюции этих течений и их структуры весьма похожи. Поэтому имеет смысл описать подробнее только один вариант, например, при ν = 25.

Как отмечено выше, потеря устойчивости осредненным стационарным течением псевдопластической жидкости и переход к колебательному режиму происходят в пределах горизонтального участка линии 1, приведенной на рисунке 2. На этом участке наблюдаются относительно слабые, близкие к гармоническим колебания, для которых амплитудные значений Nu и ψmax превышают средние значения на 1–2%. С ростом числа Грасгофа амплитуда колебаний возрастает, а сами колебания приобретают сложный характер. Для чисел Gr < 1.0 колебания являются периодическими.

Зависимости числа Нуссельта Nu и максимума функции тока ψ max от времени для Gr = 0.7 и ν = 25 при таких колебаниях содержит рисунок 8а , б . Точкам 1–8 , проставленным на временном интервале, равном периоду колебаний, соответствует рисунок 9, на котором показана эволюция полей функции тока и температуры осредненного колебательного течения. При дальнейшем увеличении числа Грасгофа (Gr ⩾ 1.0) на зависимостях Nu и ψ _max от времени невозможно выделить определенные периодические структуры. Колебания приобретают квазипериодический характер. Пример зависимости ψ max от времени для таких колебаний представлен на рисунке 8в .

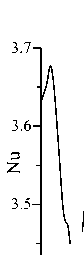
( a )

( в )

Рис. 8. Колебательные режимы при ν = 25 : периодический ( Gr= 0.7 ) ( а, б ) и квазипериодический ( Gr= 1.5 ) ( в )

Возникновение и развитие колебательных режимов в псевдопластической жидкости, аналогично тому, что наблюдалось в ньютоновской жидкости и описано в работах [43, 44] . Из этого можно сделать вывод, что источником колебаний конвективных вихрей являются тепловые волны, формирующиеся вблизи вертикальных стенок полости.

Необходимо отметить, что в данной работе не ставилась цель подробно исследовать колебательные режимы осредненной конвекции псевдопластической жидкости. Из рисунка 8 видно, что возникающие сложные колебательные режимы являются суперпозицией более простых колебаний. Наряду с основной частотой в них можно выделить дополнительные частоты. Зависимость частоты колебаний от параметров задачи — проблема, представляющая интерес для изучения.

• 4.2.    Неньютоновская мода

На рисунке 10 более подробно изображена область, которая на рисунке 2 соответствует неньютоновской моде стационарной осредненной конвекции, содержащая зависимости максимума функции тока ψ _max от числа Грасгофа Gr в другом его диапазоне для тех же значений параметров неньютоновости.

Из рисунков 2 и 10 видно, что, в отличие от решений типа ньютоновской моды, для неньютоновской моды наблюдается существенная зависимость ψ max от параметра неньютоновости. Однако структуры стационарных осредненных конвективных течений и характер их эволюции одинаковы для всех рассмотренных ν . Еще раз следует подчеркнуть, что в решениях типа неньютоновской моды в исследованном диапазоне чисел Грасгофа колебательных режимов не обнаружено. Значения Gr _c , зависящие от параметра неньютоновости, при которых происходит смена структуры течения, содержит таблица 2.

При малых значениях числа Грасгофа (Gr ⩽ 0.06 для ν = 25; Gr < 0.2 для ν = 100; Gr < 0.3 для ν = 500) при неньютоновской моде в полости реализуется слабоинтенсивное 3-вихревое течение, вид которого для случая ν = 25 и Gr = 0.01 представлен на рисунке 11. Видно, что в центральном вихре появляется два центра, и при дальнейшем повышении числа Грасгофа он разделяется на два вихря. Осредненное конвективное течение в этом случае приобретает 4-вихревой вид, характерный для термовибрационной конвекции в невесомости (см. картины полей при Gr = 0.2 и Gr = 0.7 на Рис. 11) . При относительно малых значениях числа Грасгофа изолинии поля температуры T искривлены слабо, что свидетельствует о теплопроводном механизме переноса энергии в полости.

На кривых 3 ’ дляν = 25, 3 ” для ν = 100 и 3 ”’ дляν = 500 рисунка 10 хорошо видны изломы, свидетельствующие об изменении характера течения — перестройке 4-вихревого термовибрационного конвективного течения в

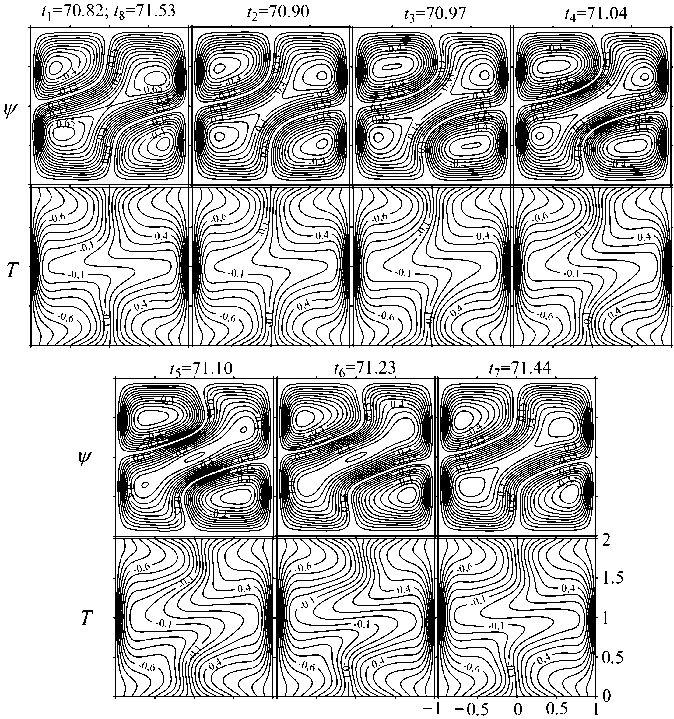
Рис. 9. Изолинии функции тока ( ψ ) и температуры ( T ) осредненного колебательного течения для Gr = 0.7 и ν = 25 в разные моменты периода колебаний

3-вихревое, которое возникает при совместном влиянии гравитационного и вибрационного механизмов генерации конвекции. Значения чисел Грасгофа, соответствующие точкам излома, представлены в таблице 2. Такое 3-вихревое течение, в котором интенсивность угловых вихрей сравнима с интенсивностью центрального вихря, содержит рисунок 11 (см. фрагменты при Gr = 1 и Gr = 3). Изолинии температуры в этом случае заметно искривляются, то есть в полости преобладает конвективный перенос тепла.

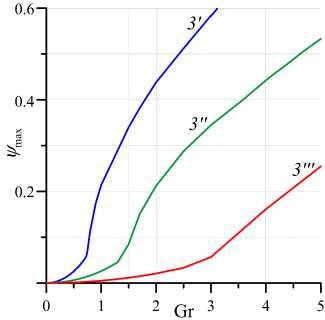
Рис. 10. Зависимость максимума функции тока ψmax от числа Грасгофа Gr для неньютоновской моды при тех же значениях параметра неньютоновости, что и на рисунке 2: кривая 3 ’ – ν = 25 ; 3 ” – ν = 100 ; 3 ”’ – ν=500

Таблица 2. Критические числа Грасгофа для неньютоновской моды, при которых происходит смена структуры течения

Номер расчета	1	2	3
ν	25	100	500
Gr c	0.73	1.4	3

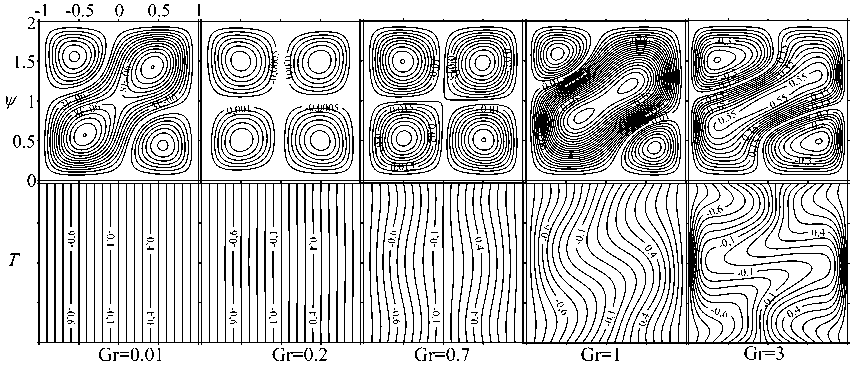
Рис. 11. Изолинии осредненной функции тока ( ψ ) и температуры ( T ) для неньютоновской моды при ν = 25

• 5.    Заключение

В работе сформулирована математическая модель термовибрационной конвекции жидкости в полости квадратного сечения, находящейся в условиях пониженной гравитации и совершающей высокочастотные линейно-поляризованные вибрации малой амплитуды вдоль направления вектора силы тяжести. Реология жидкости описывается моделью Уильямсона. На основе модели впервые достаточно подробно исследованы конвективные течения псевдопластической жидкости. Интенсивность вибрационного воздействия связывается с используемым авторами статьи вибрационным параметром, который при пониженной гравитации приобретает значения, намного превышающие единицу. Важно отметить, что для обобщенных ньютоновских жидкостей, к которым относится псевдопластическая жидкость, вибрационный параметр определяет еще и величину той составляющей осредненной вибрационной силы, которая связанна с нелинейной вязкостью. Поэтому использование вибрационного параметра в случае неньютоновской жидкости более предпочтительно, чем традиционного для задач термовибрационной конвекции вибрационного числа Грасгофа.

Расчеты показали, что при малых числах Gr (в условиях близких к невесомости) в полости реализуется медленное одновихревое стационарное конвективное течение, которое впоследствии трансформируется в 3-вихревое; увеличение числа Gr приводит к 4-вихревому конвективному течению, характерному для терморвибрационной конвекции в невесомости. При дальнейшем наращивании числа Грасгофа 4-вихревое течение вновь трансформируется в 3-вихревое, которое обусловливается совместным влиянием вибрационного и гравитационного механизмов генерации конвекции. Усиление неньютоновских свойств жидкости подавляет 4-вихревое течение, свойственное термовибрационной конвекции в ньютоновской жидкости.

При численном моделировании авторами обнаружено существование двух типов решений задачи, которые условно названы ньютоновской и неньютоновской модами. Решение первого типа — ньютоновская мода, существует у задач течения как псевдопластических, так и ньютоновских жидкостей. Решение типа ньютоновской моды в случае псевдопластической жидкости проявляет слабую зависимость структуры течений от реологических свойств жидкости. Осредненное стационарное течение, соответствующее ньютоновской моде, неустойчиво, то есть существует пороговое число Грасгофа, при котором стационарный режим сменяется колебательным. Второй тип решения — неньютоновская мода, существует только у псевдопластических жидкостей. Показано, что при ослаблении нелинейно-вязких свойств псевдопластической жидкости (в ньютоновском пределе реологической модели Уильямсона) это решение сливается с ньютоновской модой. В вязкопластическом пределе, когда жидкость становится фактически линейно-вязкой, но приобретает предел текучести, интенсивность течения, отвечающая неньютоновской моде, стремится к нулю. Осредненное стационарное течение псевдопластической жидкости, соответствующее неньютоновской моде, является устойчивым: во всем исследованном диапазоне чисел Грасгофа перехода к колебательным режимам не найдено.

Необходимо отметить, что данная работа фактически не затрагивает проблемы влияния частоты вибраций или интенсивности вибрационного воздействия на конвективное течение псевдопластической жидкости. Такие исследования в достаточно полном объеме выполнены и опубликованы авторами для ньютоновской жидкости. Все вычислительные эксперименты, представленные здесь, осуществлены лишь при одном, пусть и достаточно большом, значении вибрационного параметра. Есть предположение, что увеличение его значения совместно с усилением нелинейно-вязких свойств могут дать с использованием обсуждаемой реологической модели большое многообразие решений, для которых характерны сложные конвективные режимы.