Конвективный атмосферный перенос загрязняющей аэрозольной субстанции на произвольном наборе точек

DOI:

С математической точки зрения мониторинг экологической ситуации состоит в описании процессов эмиссии, распространения и нейтрализации загрязняющей аэрозольной субстанции в атмосферном воздухе, и есть целый ряд моделей, описывающих эти процессы. Все они в той или иной форме опираются на закон сохранения массы и для решения соответствующего уравнения используют сеточные методы (см.: [3; 4; 6; 7]). Многие модели реализованы в виде компьютерных систем для расчета распространения в атмосфере загрязняющих веществ и вполне эффективны [2]. Вместе с тем сеточные методы требуют значительных вычислительных ресурсов, поэтому весьма интересно найти решение не на сетках, а на конечных элементах.

Если на местности в ограниченной области расположены несколько станций метеонаблюдения, которые фиксируют направление и скорость ветра, то, применяя к станциям алгоритм какой-либо триангуляции, получим разбиение области на конечные элементы: треугольники этой триангуляции. Значения векторов воздушного потока, зафиксированные в вершинах триангуляции, позволяют интерполировать их линейно на каждом из треугольников и получить на каждом из них описание поля воздушного потока как функции пространственных координат. Тем самым задача конвективного переноса загрязняющей аэрозольной субстанции в интересующей нас области сводится к серии таких задач на конечном наборе треугольников.

В настоящей работе мы даем алгоритм, который позволяет, исходя из конечного набора метеорологических данных в вершинах триангуляции, получить квазирешение задачи конвективного переноса в виде кусочно-постоянной функции координат.

1.    Перенос на треугольнике

Пусть S – единичный двумерный симплекс с вершинами M ₁(0,0), M ₂(1,0) и M ₃(0,1), пусть в вершинах M_i заданы векторы v_i , означающие скорость воздушного потока, и пусть v ( x, y ) – векторное поле, которое получается линейной интерполяцией векторов v ₁, v ₂, v ₃. Рассмотрим прямую призму P высоты h , построенную на симплексе S . Если в вершинах симплекса S известны значения векторов

a v (M1) = 1 1 I, I bi)

a

v ( M 2 ) = 1 2 I ,

I b 2 )

I a^ I v ( M з ) = 1 ³ I ,

I b 3 )

а двумерное векторное поле v ( x , y ) на S получается из этих значений путем линейной интерполяции как в [10]:

I ( a ₂ - a 1 ) x + ( a 3 - a 1 ) y + a 1 I v ( x , y ) = I                                      I

I⁽ b 2 ^- b i ) x ^{+ (} b 3 ^- b i ) У ⁺ b i ) ,

то трехмерное векторное поле w ( x, y, z ) вида

। ( a ₂ - a_i) x + ( a 3 - a_i) y + a_i

^{v (} x , У ) =

⁽ b 2 ^- b i ) x +⁽ b 3 ^- b i ) y + b i

( ⁽⁽ a i ^- a 2 ) + ⁽ b i ^- b 3 )) z    )

является трехмерным расширением поля v ( x, y ) на P и удовлетворяет условию соленоидальности:

jj wd c = 0,                                             (4)

σ где о означает полную поверхность призмы P [9].

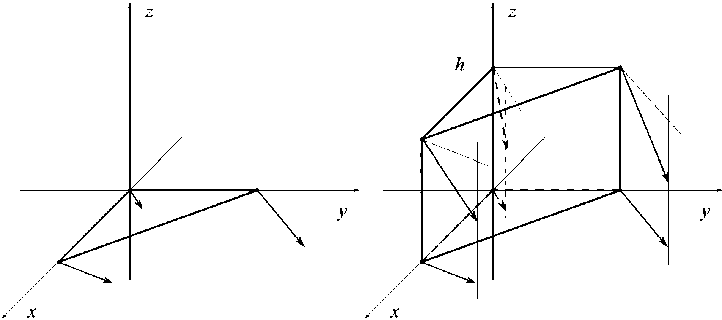
a                                           b

Рис. 1. Трехмерное расширение векторного поля:

a – двумерные векторы потока v ( x , y ) в вершинах симплекса; b – трехмерные векторы потока w ( x , y , z ) в вершинах призмы

Обозначим l_i стороны симплекса, пронумеровав их от нуля против часовой стрелки:

1₁ = M 1 M 2 , 1 2 = M 2 M 3 , 1 3 = M 3 M 1 .

Пусть о i - боковые грани призмы P , построенные на сторонах 1 , симплекса S , пусть о 0 -нижняя, а о ₄ - верхняя грань призмы P , и пусть Q i означает объем воздуха, проходящий за единицу времени через грань о i . С учетом того что объем потока, проходящий через поверхность за единицу времени, вычисляется как поверхностный интеграл, имеем

Q , = jj wd о.                                               (6)

^о ,

В [9] мы показали, что объемы Q . воздушных потоков, проходящих через грани о . призмы P за единицу времени, равны:

Q1= ^L^ h , (7) Q 2 = Г a 2 + a 3   b 2 + b 3 1                                                                            1 (   2        2 ) h, (8) q   a1 + aL h , 32, (9) Q 4 = Г a, - a2 b - b "I 2    '    2 ]h, (10) при этом Qo = 0, положительное значение Qi означает объем входящего потока, а отрицатель-ное– объем исходящего.

Пусть на гранях призмы P известна объемная плотность ρ( x , y , z ) загрязняющей аэрозольной субстанции, причем:

Р( x , У , z ) = Р , V ( x , y , z ) ео , , г * 4,                                      (11)

Р( x , У , z ) = 0   V ( x , y , z )ео 4 .

Определение 1. Пусть векторы v_i и скаляры ρ _i не зависят от времени, и пусть загрязняющая аэрозольная субстанция не диффундирует, не вступает в химические реакции нейтрализации с веществами окружающей среды и не выпадает в осадок. Решением стационарной задачи конвективного переноса на двумерном единичном симплексе S будем называть среднюю объемную плотность ρ _s загрязняющей аэрозольной субстанции внутри призмы P.

Для решения этой задачи введем понятие противоречия между сторонами симплекса и направлениями воздушного потока. Если x = T,        I x = 1 - T,        I x = 0, те [0,1],

,       l У = T,         lУ = 1-T, то векторное поле v(x, y), зависящее на симплексе S от двух переменных x и y, на его границах зависит от одной переменной τ. Обозначим vi(τ) сужение векторного поля v(x, y) на i-ю сторону симплекса.

Определение 2. Пусть n_i – вектор единичной нормали к стороне l_i , направленный внутрь симплекса. Функцией противоречия стороны l_i будем называть скалярное произведение:

5 , ^(т) =⁽ у ^(т); n , ),   ^те[0,1].

Определение 3. Сторону l_i симплекса S будем называть непротиворечивой, если ее функция противоречия не меняет свой знак на отрезке [0; 1]:

5 _! (Т 1 )3 _! (Т 2 ) > 0    V T i , Т 2 е[0,1].

В противном случае будем называть сторону противоречивой .

Определение 4. Симплекс S будем называть непротиворечивым, если все его стороны непротиворечивы. Если хотя бы одна из сторон симплекса противоречива, будем говорить, что симплекс противоречив.

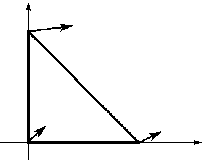
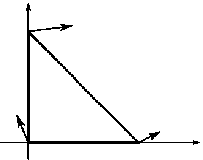
b

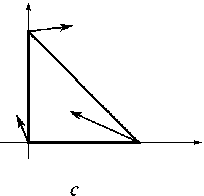
Рис. 2. Противоречия на симплексе:

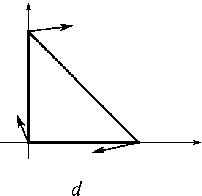
a – противоречия отсутствуют; b – противоречия на одной стороне; c – противоречия на двух сторонах; d – противоречивы все стороны

Пусть симплекс S непротиворечив, пусть на нем линейно интерполировано векторное поле v ( x , y ), которое расширено до поля w ( x , y , z ) на призме P , и пусть объемная плотность загрязняющей атмосферной субстанции постоянна на каждой грани призмы: р( x , у , z ) = p i для грани c i , причем ρ ₄ = 0 . Обозначим

1, если 5Дт ) >  0 V т е [0,1],

0, если 3 т е [0,1] такое, что 5i(T) < 0, где 8i(т) - функции противоречия сторон симплекса 1. С учетом того что поток поля w(x, y, z) не зависит от времени, а также того, что р(x, у, z) = 0 V z > h, можно показать [11], что средняя объемная плотность субстанции в призме P вычисляется по формуле:

Р s =

Z 3 = 1 8 i р i n i Z 4 = 1 8 i n i

где Q i - объемы, вычисляемые по формулам (7)-(10).

Пусть T – невырожденный треугольник с вершинами M_i ( x_i , y_i ), и пусть в его вершинах заданы векторы v_i . Линейно интерполируя значения векторов, получим векторное поле v ( x , y ), определенное на произвольном невырожденном треугольнике T , подобно тому, как это делалось выше на единичном двумерном симплексе S . Рассмотрим прямую призму P высоты h , построенную на треугольнике T . Для того чтобы поле v ( x , y ) подчинялось условию соленоидальности, необходимо расширить его до трехмерного поля w ( x , y , z ), причем, как и выше, это можно сделать следующим образом:

( V . ( x , у ) ]

V ⁽ x , у ) = |           I ,      w ⁽ x , у , z ) =

V ^V 2 ^{( x} , у ) J

' V 1 ( x , У )" ^V 2 ⁽ x , У )

v az  _?

где коэффициент а определяется исходя из закона сохранения массы в интегральной форме:

EJJ wd® = 0,                                    (19)

i=0 ai здесь o0 4 означают соответственно нижнюю и верхнюю грани призмы P, а о1 2 3 - боковые грани.

Пусть на гранях призмы P известна объемная плотность ρ( x , y , z ) загрязняющей аэрозольной субстанции, причем:

Р( x , У , z ) = Р . V ( x , У , z ) ^e ^., i * 4,                                      ⁽²⁰⁾

P( x , У , z ) = 0 V ( x , y , z ) ео 4 -                                          (2Г)

Определение 5. Пусть векторы v_i и скаляры ρ _i не зависят от времени, и пусть загрязняющая аэрозольная субстанция не диффундирует, не вступает в химические реакции нейтрализации с веществами окружающей среды и не выпадает в осадок. Решением стационарной задачи конвективного переноса на треугольнике T будем называть среднюю объемную плотность ρ _T загрязняющей аэрозольной субстанции внутри призмы P .

Если треугольник T непротиворечив в смысле определений 2–4, то, подобно (17), средняя объемная плотность ρ _T загрязняющей субстанции внутри призмы P вычисляется как отношение объемов:

_ e 3 = , 5 . p . n .

PT         .4           ,

E ₽. 5П где П1 2 з - объемы воздушных потоков, проходящих за единицу времени через боковые грани призмы P; П4 - объем, проходящий через ее верхнюю грань, а коэффициенты 5. равны 1 для входящих потоков, и 0 для исходящих.

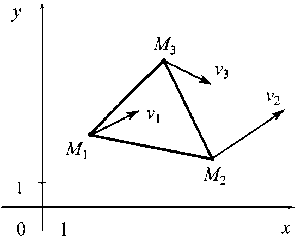
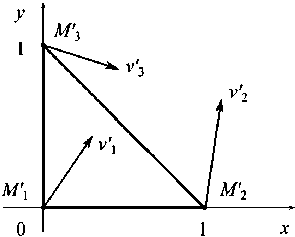
Аффинно преобразуя плоскость, задачу конвективного переноса на треугольнике T можно свести к задаче на симплексе S .

a

Рис. 3. Переход от данных на треугольнике T к данным на симплексе S : a – исходный треугольник T ; b – результирующий симплекс S

b

Определение 6. Стандартизирующим аффинным преобразованием будем называть аффинное преобразование, переводящее треугольник T в двумерный единичный симплекс S .

Понятно, что если треугольник T обладает вершинами M ( x , y ), то стандартизирующее аффинное преобразование задается следующей заменой:

x

y

x ₂

y ₂

— x ,

^- У 1

x ₃

y ₃

-

x ₁

-

y ₁

x ' y '

+

x ₁

y ₁

причем под действием преобразования (23) вершины треугольника T переходят в вершины симплекса S :

M i ( X i , У 1 ) ^ M 1 (0,0), M 2 ( x 2 , y 2 ) ^ M '₂ (1,0), M з ( x 3 , y 3 ) ^ M 1(0,1),                    (24)

а векторы v_i в вершинах треугольника T – в векторы v’_i в вершинах симплекса:

vi

a i 1              I a ' i 1 I x 2 - x 1

I ^ v ' i = I     1 = 1

. M        I b i ) I y 2 ^- У 1

x ₃

y ₃

-

-

x ₁

y ₁

- 1

ai bi

Преобразование (23) сохраняет отношение объемов, поэтому для того, чтобы получить решение (22) на треугольнике T , достаточно перевести данные на симплекс S и найти решение в виде (17), применяя формулы (7)–(10) для вычисления объемов.

2.    Перенос на произвольном наборе точек

Пусть на плоскости задан конечный набор точек M_i , и в каждой из точек задан вектор v_i . На выпуклой оболочке Conv( M_i ) построим прямую призму P высоты h , и пусть присутствующая в атмосфере загрязняющая аэрозольная субстанция обладает постоянной плотностью ρ _i на боковых гранях призмы P и нулевой плотностью на ее верхней грани.

Определение 7. Пусть векторы v_i и скаляры ρ _i не зависят от времени, и пусть загрязняющая аэрозольная субстанция не диффундирует, не вступает в химические реакции нейтрализации с веществами окружающей среды и не выпадает в осадок. Пусть Tr – какая-либо триангуляция точек M_i , состоящая из треугольников T_i :

Tr = { T 1 , T 2 ,..., T n } .                                                        (26)

Квазирешением стационарной задачи конвективного переноса на наборе точек M_i будем называть набор решений на треугольниках T_i :

P 1 , P 2 ,..., P n ,                                                                 ⁽²⁷⁾

полученных в смысле определения 5.

Определение 8. Решением стационарной задачи конвективного переноса на наборе точек M_i будем называть непрерывную функцию ρ( x , y ), интерполирующую значения (27) .

Если все треугольники триангуляции Tr непротиворечивы, будем говорить, что триангуляция Tr непротиворечива. Треугольник непротиворечивой триангуляции будем называть корректно определенным, если известны плотности ρ _i на всех входящих относительно поля v ( x , y ) боковых гранях прямой призмы P , построенной на этом треугольнике ². Класс корректно определенных треугольников триангуляции Tr будем обозначать CD ( Tr ) .

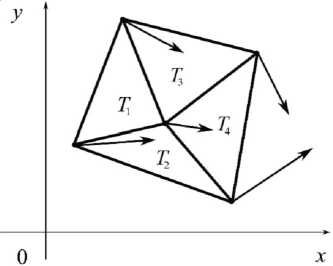
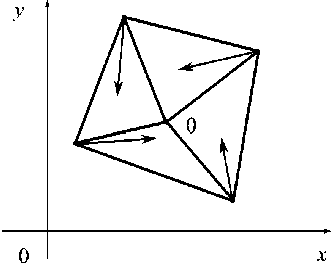
Например, если набор из пяти точек M_i триангулирован как на рисунке 4, и направления векторов v_i таковы, как на рисунке 4 а , то все треугольники триангуляции Tr непротиворечивы и среди них имеется один корректно определенный треугольник T ₁ . После решения задачи на треугольнике T ₁ корректно определенными становятся треугольники T ₂ и T ₃ . После решения задачи на треугольниках T ₂ и T ₃ корректно определенным становится треугольник T ₄ . Таким образом, на каждом из треугольников триангуляции последовательно получаются решения в смысле определения 5, а совокупность этих решений образует квазирешение на триангуляции в смысле определения 7. Если же направления векторов v_i таковы, как на рисунке 4 b , то среди треугольников триангуляции них нет ни одного корректно определенного, и решить задачу ни на одном из них нельзя.

a

Рис. 4. Корректно и некорректно определенные треугольники:

b

a – в триангуляции имеется корректно определенный треугольник T ₁; b – в триангуляции нет ни одного корректно определенного треугольника

Однако решение возможно на объединении таких треугольников. Пусть tr ⊂ Tr – подмножество треугольников из Tr , и пусть D – объединение треугольников из tr. Область D будем называть корректно определенной, если известны плотности ρ _i на всех входящих относительно поля v ( x , y ) боковых гранях прямой призмы P , построенной на этой области. Если корректно определенная область D является связной, то решение стационарной задачи конвективного переноса на ней получается аналогично (22). А именно: пусть σ ₁ , σ ₂ , ..., σ _k – боковые грани прямой призмы P_D , построенной на области D , и пусть Ω _i – объемы потоков, проходящих через эти грани за единицу времени. Пусть σ _{k + 1} – верхняя грань призмы P_D . Тогда объем потока, проходящего через верхнюю грань, вычисляется в силу закона сохранения массы:

k

Ω k + 1 =- ∑ Ω i .                                        ⁽²⁸⁾

i = 1

Объемы на боковых гранях вычисляются при помощи стандартизирующих аффинных преобразований (23), после выполнения которых применяются формулы (7)–(9), и каждый из полученных объемов умножается на модуль якобиана соответствующего стандартизирующего аффинного преобразования. После этого средняя объемная плотность загрязняющей аэрозольной субстанции внутри призмы P_D вычисляется как отношение объемов:

ρ _D

∑ _i ^k _{= 1} δ i ρ i Ω i ∑ i ^k =⁺ 1^{1 δ} i ^Ω i

где коэффициенты δ _i равны 1 для входящих потоков, и 0 – для исходящих.

Таким образом, для любой непротиворечивой триангуляции имеется алгоритм вычисления квазирешения задачи конвективного переноса в смысле определения 7. Последовательность исполнения алгоритма такова.

Шаг 1. Обозначим Tr ₀ исходную триангуляцию: Tr ₀ = Tr . Допустим, среди треугольников триангуляции Tr ₀ имеется хотя бы один корректно определенный треугольник T_{i 0} . Решая задачу на треугольнике T_{i 0} , получаем решение ρ _{i 0} .

Шаг 2. Исключим треугольник T_{i 0} из триангуляции Tr ₀ , получим триангуляцию Tr ₁ = Tr ₀ \ T_{i 0} . Допустим, среди треугольников триангуляции Tr ₁ имеется хотя бы один корректно определенный треугольник T_{i 1} . Решая задачу на треугольнике T_{i 0} , получаем решение ρ _{i 1} .

Шаг 3. Исключим треугольник T_{i 1} из триангуляции Tr ₁ , получим триангуляцию Tr ₂ = Tr ₁ \ T_{i 1} .

И так далее.

Шаг k. Допустим, в k-й триангуляции Trk=Trk-1\Tik-1 нет ни одного корректно определенного треугольника. Тогда объединение всех еще не исключенных треугольников является корректно определенной областью. Обозначим ее D. Если область D является связной, то, применяя (29), решаем на ней задачу и найденное значение ρD присваиваем всем треугольникам области D. Если же область D состоит из нескольких компонент связности, то поступаем точно так же с каждой из компонент связности.

3.    Пример

Пусть на местности имеется одиннадцать станций метеонаблюдения, и пусть эти станции зафиксировали одиннадцать значений ветрового потока. Обозначим станции M_i , а полученные от них значения ветрового потока будем считать двумерными векторами v_i , приложенными к этим точкам.

M 1 (2,8);	v = (0,0);	M 2 (5,15);	v 2 = (1,-1)
M 3 (6,2);	v з = (1,1);	M 4 (8,10);	v 4 = (2,1);
M 5 (11,16);	v 5 = (3,0);	M 6 (12,5);	v 6 = (0,0);
M 7 (13,9);	v 7 = (2,1);	M 8 (17,1);	v 8 = (1,0);
M 9 (17,7);	v 9 = (1,2);	M 10 (18,13);	v 10 = (3,1);
M 11 (20,9);	v 11 = (2,2).

Пусть везде на границе выпуклой оболочки Conv( M_i ) средняя объемная плотность загрязняющей атмосферной субстанции постоянна и равна ρ, и везде выше высоты h ее плотность равна нулю. Требуется описать функцию плотности внутри выпуклой оболочки Conv( M_i ) как непрерывную функцию координат ρ( x , y ).

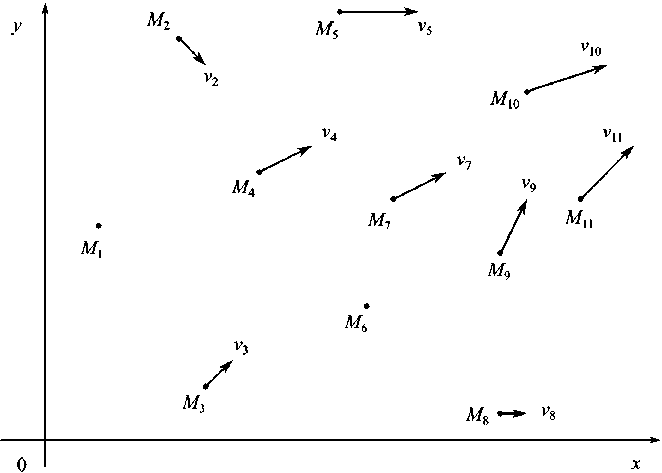
Рис. 5. Набор скоростей воздушного потока в точках M_i

Применим к точкам M_i алгоритм какой-либо триангуляции. Получим триангуляцию Tr , состоящую из тринадцати треугольников T_ijk , каждый из которых нумеруется тремя индексами своих вершин M_i , M_j и M_k .

^Tr = ^{ T 1,2,4 , ^T 1,3,4 , ^T 2,4,5 , ^T 3,4,6 , ^T 3,6,8 , ^T 4,5,7 , ^T 5,4,7 , ^T 5,7,10 , ^T 5,7,9 , ^T 6,8,9 , ^T 7,9,10 , ^T 5,9,11 , ^T 9,10,11 ^{} .}

Мультииндексы ijk упорядочены лексикографически. Для упрощения обозначений занумеруем треугольники в порядке их возрастания (см. рис. 6):

Tr = ^{T 1 , T 2 , T 3 , T 4 , T 5 , T 6 , T 7 , T 8 , T 9 , T 10 , T 11 , T 12 , ^T 13 ^{} .                                        (32)}

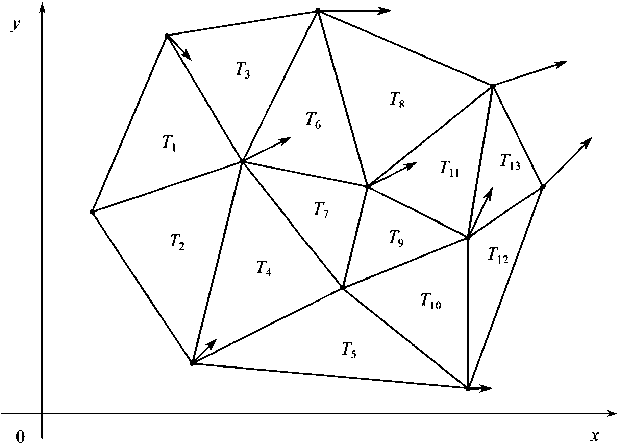
Рис. 6. Триангуляция исходного набора точек и наблюдаемые векторы скорости в вершинах триангуляции

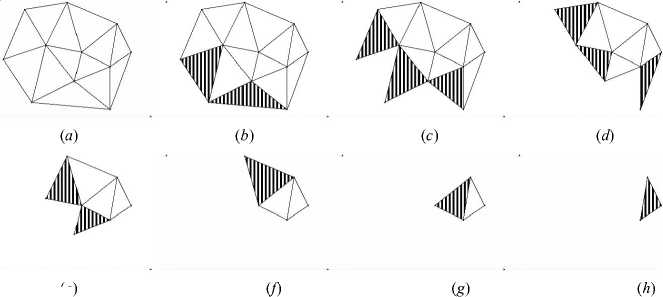
Все ребра триангуляции Tr непротиворечивы. Следовательно, триангуляция Tr непротиворечива. Обозначим Tr ₀ = Tr . Среди треугольников триангуляции Tr ₀ лишь два принадлежат классу корректно определенных: T ₂ , T ₅ e CD ( Tr ₀ ) . Пусть теперь Tr 1 = Tr₀ \ { T ₂, T₅ } . Среди треугольников триангуляции Tr 1 три треугольника принадлежат классу корректно определенных: T 1 , T ₄, T ₁₀ e CD(Tr 1 ) . Снова обозначим Tr ₂ = Tr 1 \ { T 1 , T ₄ , T ₁₀ } и т. д. (рис. 7):

Tr₀ = Tr

Tr = Tr 0\ { T 2 , T 5 }

Tr = Tr1\ { T 1 , T 4 , T 10 }

Tr 3 = Tr 2 \ { T 3 , T 7 , T 12 }

TA = Tr₃\ {T 6 , T 9 }

Tr 5 = Tr 4\ { T }

Tr ₆ = Tr 5\ { T 11 }

T 2 , T 5 e CD ( Tr 0 )

T 1 , T 4 , T 10 e CD ( Tr 1 )

T 3 , T 7 , T 12 e CD ( Tr 2 )

T 6 , T 9 e CD ( Tr 3 )

T 8 e CD ( Tr 4 )

T 11 e CD ( Tr 5 )

T 13 e CD ( Tr 6 )

Средняя объемная плотность ρ _i вычисляется в порядке, заданном триангуляциями (33):

^p 2 , ^P 5 ^ P 1 ,^p 4 , P 10 ^ ^p 3 , ^p 7 ,P 12 ^ Р б ,^P 9 ^ ^p 8 ^ P 11 ^ P 13 .

( e )

Рис. 7. Последовательность прохода корректно определенных треугольников в триангуляциях Tr ₀, … Tr ₆

Вычислим сначала среднюю объемную плотность ρ ₂ .

Так как треугольник T ₂ обладает вершинами (2,8), (6,2) и (8,10), то под действием следующего стандартизирующего аффинного преобразования

Г 4   6 А Г x ' A

(- 6 2 J y'J

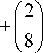
он переходит в единичный симплекс S с вершинами (0,0), (1,0) и (0,1) соответственно. Далее, так как

Г 4  6 A " 1_J_ Г 2 - 6 A

(- 6 2J = 44 (6 4 J ,

то векторы в вершинах симплекса приобретают следующие координаты:

1 Г 2 - 6 Af о А_Г о A 44 ( 6 4 J о > о J ,

1 Г2 - 6 А Г1А_ Г- 4A 44 (6   4 J|jJ = 44 (10 J ,

1 Г 2 - 6 Y 2 A_ 1 Г-2 A 44 (6   4 JI 1 J" 44 (16 J ,

где вектор v ' ₁ привязан к точке (0,0), вектор v ' ₂ привязан к точке (1,0) и вектор v ' ₃ привязан к точке (0,1).

Пусть теперь P ’– прямая призма высоты h , построенная на симплексе S . Пользуясь известными координатами векторов v ' i , по формулам (7)-(10), вычисляем объемы Q ' i потока воздуха, проходящие через боковые и верхнюю грани призмы P ’. Имеем:

Q'. = — h , Q' =-¹⁰ h , Q' =-— h , Q' = — h .

1   44        2     44        3     44        4   44

С учетом того что через верхнюю грань в призму P ’ поступает воздух с нулевой плотностью загрязняющей субстанции, средняя объемная плотность в призме P ’ на симплексе S равна:

p Q 1p = _5 p ^ 0,45p, s Q', +Q'4   11

а это, в силу аффинной инвариантности средней объемной плотности, означает, что P2 * 0,45p.

Аналогично, отталкиваясь от треугольника T ₅ триангуляции Tr ₀, при помощи стандартизирующего аффинного преобразования

Г11 6 А Г x ' А I-1 3 JI У 'J

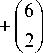
вычисляем значение средней объемной плотности ρ₅: ρ ₅ = ρ.

После этого исключаем из триангуляции Tr ₀ треугольники T ₂ и T ₅ и переходим к триангуляции Tr ₁ , в которой корректно определенными являются треугольники T ₁ , T ₄ и T ₁₀ . Выполняем нужные стандартизирующие аффинные преобразования, вычисляем ρ ₁ , ρ ₄ и ρ ₁₀ и т. д.

Окончательно, после прохода всех триангуляций вплоть до Tr ₆ , имеем следующие значения средней объемной плотности ρ _i на треугольниках T_i :

ρ1 ≈ 0,73ρ; ρ2 ≈ 0,45ρ; ρ3 ≈ 0,77ρ; ρ4 ≈ 0,38ρ ρ5 = 1,00ρ ρ6 ≈ 0,51ρ; ρ7 ≈ 0,25ρ; ρ8 ≈ 0,51ρ; (45) ρ9 ≈ 0,17ρ; ρ10 ≈ 0,17ρ; ρ11 ≈ 0,19ρ; ρ12 ≈ 0,08ρ; ρ13 ≈ 0,17ρ; и этот набор значений является квазирешением задачи конвективного переноса на триангуляции Tr. Если каждое из значений ρi привязано к конкретной точке внутри треугольника Ti (например, к центроиду треугольника), то, триангулируя эти точки, можно легко получить решение в смысле определения 8 путем линейной интерполяцией значений ρi.