Кооперативный вариант игры преследования с двумя преследователями и одним убегающим: сильная устойчивость множества дележей

Задачи преследования являются типичными примерами дифференциальных игр. Задачи преследования с простым движением стали базовыми для современной теории дифференциальных игр. Несмотря на внешнюю простоту постановки, многие из них в настоящее время представляют собой серьезные математические проблемы.

Естественным подходом к изучению игр простого преследования является рассмотрение данных задач как кооперативных дифференциальных игр. В этом случае особую роль играет концепция динамической устойчивости (состоятельности во времени). Нарушение динамической устойчивости 240

принципа оптимальности приводит к возможности отклонения от первоначально выбранной схемы оптимального поведения и к нарушению устойчиво- сти процесса в целом.

В статье рассматривается случай преследования двумя согласованно действующими игроками P = {P1, P2} одного убегающего игрока Е; игра Г(2,1;{P1, P2}, E). Игроки перемещаются на плоскости с постоянными ско- ростями, имея возможность в каждый момент времени изменять направление своего движения (простое движение [1–2]). Преследуемый Е считается пой- манным, как только найдется такое

i е{1,2}, что местоположения Pi и Е в некоторый момент совпадают.

Будем предполагать, что в каждый момент времени наряд преследователей P = { P 1 , P₂ } имеет информацию о своем местоположении, местоположении игрока Е и направлении скорости игрока Е . Преследуемый Е имеет информацию о своем местоположении и местоположении наряда преследователей Р . Кроме того, в каждый момент времени игроки могут выбирать направление своего движения или направление вектора скорости (величина скорости постоянна и равна и . для P i е P и v для Е) ; u i >  v , i = 1,2, в остальном скорости игроков произвольны.

Выигрыш Е определяется как время встречи с первым из преследующих игроков, умноженное на количество преследующих игроков. Выигрыш P = { P 1 , P 2 } определяется как величина выигрыша Е с обратным знаком.

Обзор литературы

Задачам преследования с простым движением посвящен ряд работ [1–5]. Определение лучших способов преследования и убегания, выяснение возможности встречи – вот основные вопросы, которые рассматривались в этих работах. При исследовании дифференциальных игр простого преследования часто используется методология кооперативной теории игр [4– 7]. Вопрос в этом случае осложняется тем, что в данных задачах необходимо исследовать динамическую устойчивость принципа оптимальности.

Впервые проблема динамической устойчивости решений в дифференциальных играх была выявлена Л. А. Петросяном [6; 8–9]. Исследователем было предложено несколько подходов к преодолению проблемы динамической неустойчивости, заключающихся в определенной «регуляризации» принципов оптимальности, заимствованных из статической теории игр [7; 10–12]. Интерес к указанным вопросам проявился также

MORDOVIA UNIVERSITY BULLETIN у западных исследователей, в работах которых проблема получила название «time-consistency problem» (проблема состоятельности во времени) [13–14]. Отдельного внимания заслуживает исследование F. E. Kidland, E. C. Prescott [15]. Следует отметить, что в упомянутой работе не было предложено способов преодоления проблемы несостоятельности во времени, что крайне важно для экономических и других приложений.

Материалы и методы

В статье был предложен метод нахождения оптимальных стратегий игроков с использованием геометрического подхода. В качестве такой стратегии для наряда преследователей была выбрана стратегия параллельного сближения ( П -стратегия). При переходе к рассмотрению исследуемой игры простого преследования как кооперативной дифференциальной игры использовался минимаксный метод построения характеристической функции.

Результаты исследования

Рассмотрим игру Г ( 2,1; { P , P₂ } , E ) . Будем говорить, что решение игры Г ( 2,1; { P 1 , P 2 } , E ) = Г (2,1) сводится к решению игры Г (1,1), если оптимальное время преследования в игре Г (2,1) совпадает с оптимальным временем преследования в одной из игр Г ( Р ₁, Е ) или Г ( Р ₂, Е ), т. е. для обеспечения встречи за оптимальное время наличие в наряде P = { P 1 , P 2 } одного из преследователей является излишним.

Будем говорить, что наряд применяет П -стратегию, если каждый преследователь P_i из наряда Р применяет П -стратегию [1–2].

Предположим, что выигрыши трансферабельны для игроков Р₁ и Р₂ . Принимая во внимание, что в коалиции могут вступать только игроки Р₁ и Р₂ , вычислим значения характеристической функции:

v ( P_x;t о , x о ) = val Г ( 1,1; P °, E ⁰) = - ^’’'E ) A — _^,

U - v         u 1 - v

V ( P<;1 0 , x 0 ) = val Г ( 1,1; P 2 ⁰, E ⁰)

P ( P 2 ⁰, E 0 )   A a ₂₁

- --- , u 2 - V          u 2 - V

v ( { P,P } ; 1 0 , x 0 ) = val Г ( 2,1; { p ⁰, P 2 ⁰ } , E ⁰) .

Решение игры Г ( 2,1; { p°,P₂ } , E ⁰) имеет следующий вид [1–3] (см. рис. 1): игрок Е движется в точку E ^T : p ( E ⁰, E^t ) = max p ( E ⁰, E ) , а (С) пред- s ' ⁶( C )

ставляет собой пересечение кругов

Аполлония (С₁) и (С₂ ) в играх между Р₁ и Е и Р₂ и Е . Следовательно, v ( { p , P ₂ } ; 1 ₀, x ₀ ) = - 2 T . Таким образом, оптимальной для наряда P = { P 1 , P₂ } является П -стратегия, оптимальным для Е - движение по полупрямой [ E ⁰ E ^T ] .

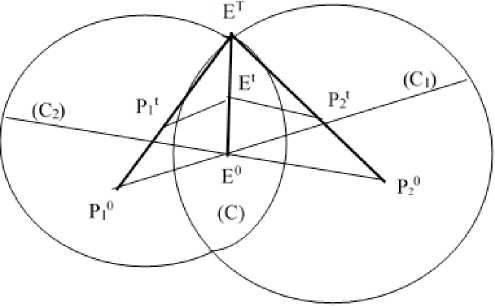
Р и с. 1. Оптимальные стратегии игроков Р₁, Р₂ и Е

F i g. 1. Optimal strategies of players P₁, P₂ and E

Чтобы игра имела содержательный смысл, сделаем некоторые предположения:

а) max

Р ( P", E ⁰) p ( P 2 ⁰, E ⁰) U - v ’ u ₂ - v

б) в дальнейшем будем рассматривать только те начальные местоположения P ⁰, P ₂⁰, E ⁰, для которых ( C ) * 0 , ( C 1 ) ^ ( C 2 ) , ( C 2 ) ^ ( C 1 ) .

Под решением будем понимать все множество дележей

M ( 1 ₀, x ₀ ) = { a = ( « 1 , a ₂

a >  v ( p ; 1 0 , x 0 ) , i = 1,2, « 1 + a 2 = v ( { P i ,P 2 } ; 1 0 , x 0

a 1

>- ^11

u 1 - v

« 2

> - ^21

u ₂ - v

a1 + a2 = -2T

Чтобы не иметь дела с отрицательными числами, вместо системы (1) будем рассматривать систему

t

а ( t ) = j P , ( t ) h ( x T ) ) d T ,       (3)

t ₀

a1 <

^a ii

u₁ - v

a2 <

^a 21

u 2 - v

что дележ α представим в виде a = a ( t ) и для всех t e [ t ₀, T ] существует такое подмножество M '( T - t , x ( t ) ) множества M ( T - 1 , x ( t ) ) , что

a1 + a2 = 2T

a ( T ) e { a ( t ) + M '( T - 1 , x ( t ) ) } c M ( T - 1 ₀, x ₀ )

Поскольку —— + —— > 2T, мно-u1 - v u 2 - v жество решений системы (2) не является пустым (t0 = 0).

Оптимальные траектории игроков показаны на рис. 1.

В случае дифференциальной игры характеристическая функция, заданная на семействе всех подмножеств мно- жества игроков, зависит от времени. Это приводит к изменению решения кооперативной дифференциальной игры в каждый момент времени. В связи с этим логично поставить вопрос об устойчивости рассматриваемых решений [6; 8; 16–17].

Пусть E ( T - t , x ( t ) ) - множество дележей в игре Г ( T - t , x ( t ) ) , t e [ t ₀, T ] . Под решением кооперативной дифференциальной игры Г ( T - t , x ( t ) ) понимается некоторое подмножество M ( T - t , x ( t ) ) c E ( T - t , x ( t ) ) , t e [ t ₀, T , где x ( t ) - оптимальная траектория движения игроков в рассматриваемой игре [5–6; 9].

Дележ a e M ( T - t ₀, x ₀ ) будем называть слабо (сильно) устойчивым в кооперативной дифференциальной игре Г ( T - t ₀, x ₀ ) с трансферабельными выигрышами, если существует интегрируемая на [ t ₀, T ] вектор-функция в ( т ) и такая вектор-функция a ( t ) ,

( a ( T ) e { a ( t ) + M ( T - 1 , x ( t ) ) } c M ( T - 1 ₀, x ₀ ) ) .

Решение M ( T - 1 ₀, x ₀ ) называется слабо (сильно) устойчивым, если слабо (сильно) устойчивы все входящие в него дележи [4–5;7;10].

Покажем, что все множество дележей рассматриваемой игры сильно устойчиво, т. е. множество решений системы al <-v(P1;t,x( a2t <-v(P2;t,xi

ait+a2 t =- v ({P, P2}; t,x (t))

не является пустым, и для каждого a e M ( 1 0 , x 0 )

a, = a,(T) = Jp^z)dT, i = 1,2, t0

a ( T ) e { a ( t ) + M ( t , x ( t ) ) } c M ( 1 0 , x 0 ) . (5)

Вычислим значения характеристи ческой функции в момент t, t e[10,T]: :

P P t , E t

v ( P. ; t , x ( t) ) = - ( i , ) , i = 1,2;

ui - v v ({Pi, P2}; t, x (t )) = -2 (T -1).

Из заданного подобия треугольников A Pt0E0ET и A P*E*ET имеем, что р( P, Et ) =

I P⁰ E ⁰| ■ | E ' E ^r|

E ^t E ^T

Итак,

v ( p ; t , x ( t

E ⁰ E ^T

E ⁰ E ^T

р ( P 0 , E ⁰ )

-

-

t

« i 1

T J и

-

v

,

i = 1,2.

E ⁰ E ^t

E 0 E

р ( р °, E ⁰ ) = ( 1 - T j р ( P °, E ⁰) .

Доказательство. Составим урав-

нение прямой ОА ⁰ (см. рис. 2, система

координат хОу):

Система (4) примет вид

y

x

t

t

t

« 11

T ) и₁

—

v

t

^а 21

T J и ₂

—

v

= 2 (T — t)

.

Поскольку

t

—

« 11

T

+

« 21

u ₁

—

v

u ₂

—

v

> 2 ( T — t ) ,

множество решений системы (6) не яв-

ляется пустым. Осталось

справедливость (5).

доказать

Предварительно докажем

две лем-

мы.

Лемма 1. «Точки»

/

A ⁰

2 T

—

« 21

« 21

к

u ₂

—

v

u ₂

—

v

и

« 21

2 T

—

« 21

,

u ₂

—

v

u ₂

—

v

y =

а 21

2 T ( и ₂

—

v)

—

« 21

x ,

k ⁰

« 21

2T ( и ₂

—

v)

—

« 21

.

Составим уравнение прямой ОА ^t :

y

x

—

t

« 21

T ) и ₂

y =

—

v

2 ( T — t ) — l 1

2 ( T — t ) — 1 1

2T ( и 2

k t =

—

« 21

u ₂

—

v

—

t

t

« 21

T ) и ₂

^а 21

T ) и ^

—

v

—

v

,

а ₂₁

—

v )— а 21

« 21

x ,

A =1 2 ( T — t ) —1 1 — - |-к             к     T J и.

а ₂₁

—

v

;

t

—

« 2\

T ) и 2

—

v

лежат на одной прямой.

2T ( и ₂

—

V )— «21

.

Поскольку k ⁰

= k t и прямые ОА ⁰

и ОА ^t

пересекаются, то они совпадают.

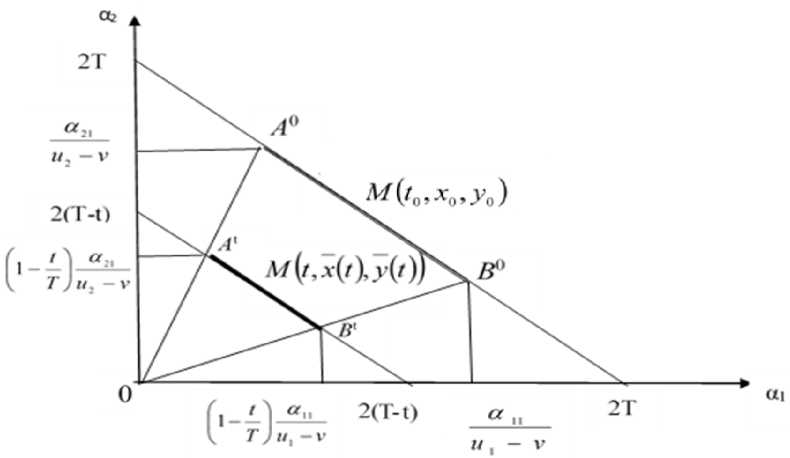
Р и с. 2. Прямые ОА ⁰ и ОА ^t ( ОB ⁰ и ОB^t ) совпадают

F i g. 2. Straights lines ОА ⁰ and ОА^t ( ОB ⁰ and ОB^t ) coincide

Лемма 2. «Точки» B ⁰ =| “^п ; 2T - “^п | и

( u₁ - V       u₁ - V J

B =|| 1 - L | ^a ; 2 ( T - t ) -| 1 - 1 1 ^ 1"- I лежат на одной прямой.

(( T J u₁ - v ^{v 7} ( T J u₁ - v J

Доказательство леммы 2 аналогично доказательству леммы 1.

В силу выпуклости множества дележей достаточно доказать справедливость (6) только для двух дележей:

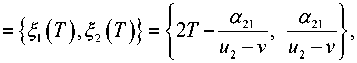
п(T) = {n (T),72 (TM^", 2T -a [ U - v u1 -

^( T ) = {^1 (T), ^2 (T)}:

^1 (T ) = 2T - ^2^ = T З^Чт ^dr; u 2 - V 0

в качестве Д ^{( 1 )} ( r ) примем — 2 T--—

1                 T (     u 2 - v в1(1(т) = TI 2T -

^a 21

= 2 -

u ₂ - V

^a 21     .

( u ₂ - v ) T ’

^2 ( T ) =

^a 2i

T

—

= J Pi4^T d p,.

А^ ( ^ ) =

^u 2 _i ^{— v} 0

в качестве P ₂ () ( t ) примем

^a 2i

( u 2

—

v ) T ,

= -1 2 T —

^a ii

T

= 2

—

^a ii

A^ ( ^T ) =

^a 2i

u ₁

—

v

( u i ^— v ) ^T '

( ^U 2

—

v ) ^T .

£( T )e{^( t ) + M ( t, x ( ti)!' M ( t 0, x0 )

n ( T ) = { П 1 ( T ) , П ( T ) } :

П(T ) =

^a ii

u ₁

—

v

T

= J pU(T dd;;

в качестве P ^{( 2 )} ( г ) -

^a ii

( u i ^— v ) ^T ’

P ^{( 2 )} ( t ) =

^a ii

(ui — v) T

;

П (T ) = 2T

—

^a ii

u ₁

—

v

T

= J pU(TТ

в качестве в-^² ( t ) - ^ 1 2 T

—

^a ii

u ₁

—

v

,

2 T

—

^a 2i

2 T

—

2 T

—

2 T

—

u 2 — a 11	v
u i —	v
a 2i
u 2 —	v
a 11
u i —	v

2 T

< 2 (T — 1) — I 1

—

t

t

^a 2i

T J u ₂

—

v

t

^a ii

T J u _i

—

v

или

—

2 T

—

2 T

—

2 T

—

и п ( T ) e { n ( t ) ⁺ M ( t , x ( t ) ) } ' M ( t 0 , x о ) в силу справедливости лемм 1 и 2 эквивалентно системе линейных нера-

венств

t

^i (T)< ^i1 +Jв2(т)dr < ni (T),

t

П2 (T )< ^21 +J в2 ^(t )dT < ^2 (T),

^i (T) < ni1 + JPi^ (T)dT < n (T),

П2 ( T ) < П21 + J P^ (T )dT < ^2 ( T)

^a 2i

T J u ₂

—

t

+ J 2

—

t

+ J 2

—

< 2(T — 1) —| i —11-I T J u

^a 2i

u ₂

—

v

^a ii

u ₁

—

v

^a 2i

u ₂

—

v

^a ii

u ₁

—

v

Распишем (7):

t

^a ii

v 0 ( u _i — v ) T

dlT <

^a ii

u ₁

—

v

,

^a ii

(ui — v) T

dT <

^a 2i

u ₂

—

v

,

^a 2i

( u ₂ — v ) T

dT <

^a ii

u ₁

—

v

,

^a ii

t

—

- + ' — v о (u 2

^a 2i

—

v) T

dT<

^a 2i

u ₂

—

v

^ . (7)

< 2 ( T — 1 ) —I i — ¹ I^V I     T J u.

^a 2i

—

^v   ( ^u i

a _ii 1

—

t

^a 2i

T J u ₂

+ 2 1

—

a _ii 1

—

v

( u i ^{— v} ) ^T

t

^a ii

T J u _i

+ 2 1

—

a _2i 1

<

^a ii

—

v

( u 2

—

v ) T"

u ₁

—

v

,

<

^a 2i

u ₂

—

v

,

.

<

^a ii

v ) T U i

—

v

,

< 2 ( T — 1 ) —I i — ¹ II T J u

^a ii

—

v ( u ₂

a _2i 1

—

<

^a 2i

v ) T"

u ₂

—

v

Легко показать, что система двойных линейных неравенств (8) имеет решение только в том и только том случае, когда

α ¹¹ + α ²¹ ≥ 2 T .          (9)

u ₁ - vu ₂ - v

Поскольку (9) действительно имеет место, то сильная устойчивость множества дележей доказана.

Обсуждение и заключения

В работе приводятся оптимальные стратегии, а также оптимальные тра-

ектории движения игроков. Выбранный принцип оптимальности оказался сильно динамически устойчивым и, следовательно, игроки не имеют оснований для окончания игры.

Попытки применить динамически неустойчивые (несостоятельные во времени) принципы оптимальности для прикладных задач в области экономики, менеджмента, охраны окружающей среды и т. д., как правило, приводят к грубым ошибкам, в результате которых принятые «оптимальные» решения оказываются нереализованными.

Поступила 14.03.2017; принята к публикации 28.04.2017; опубликована онлайн 14.06.2017

Все авторы прочитали и одобрили окончательный вариант рукописи.

248                                                      Физико-математические науки

Submitted 14.03.2017; revised 28.04.2017; published online 14.06.2017

All authors have read and approved the final version of the manuscript.