Координатный метод как один из рациональных способов решения стереометрических задач

Метод координат или координатный метод является одним из алгебраических способов решения задач. Достоинство этого метода заключается в том, что при решении применяется несколько формул и стандартный алгоритм. Имеется и недостаток. Формулы с трудом даются запоминанию, и в них легко допустить ошибку. Также необходимо подобрать такую систему координат, чтобы вычисления были не затруднительными. В дальнейшей работе подробно рассмотрим весь алгоритм решения и ситуации выбора системы координат.

Для начала дадим некоторые определения. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикулярно опущенного из этой точки на данную плоскость [1].

Чтобы найти расстояние при помощи нашего метода, используем формулу р(М, (АВС)) = ^-0===+^, где точка М(х о ; у о ; Z q ) не лежит на плоскости а: Ах + Ву + Cz + D = 0, за буквы А, В, С, D обозначим коэффициенты уравнения плоскости.

Угол между прямой и плоскостью – это угол между этой прямой и её проекцией на эту плоскость, где прямая не перпендикулярна плоскости [1, c. 43].

При использовании приведенного метода нет необходимости построения проекций, а важно лишь положение точек, принадлежащие данной прямой и плоскости.

Угол между прямой и плоскостью обозначим а = Z(a,(ABC)) = Z(a, b), где другая прямая b принадлежит плоскости АВС. Из уравнения плоскости найдем вектор нормали и, координатами которого являются коэффициенты: n = {A; B; C} . Поэтому, чтобы найти угол между прямой и плоскостью, будем искать угол между прямой и этой нормалью, зная определение скалярного произведения векторов:

cos в =

5 • а

I a\ - \n\

а^п    -

Поэтому В = arccos _ _  будет

|аНп|

нашим необходимым углом.

Теперь рассмотрим использование приведенного метода на примере решения стереометрических задач под 14 номером из ЕГЭ по математике профильного уровня.

Задача 1. Пусть дана пирамида SABCD, в основании которого лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер равны AS = VTT,SB = 3^3, SD = 2V5.

• 1)    Доказать, что ребро AS является высотой пирамиды.

• 2)    Найти угол между прямой SC и плоскостью ASB.

Выполним доказательство. Если в задаче необходимо доказать, что одна из боковых ребер пирамиды является высотой, то наш рисунок примет вид – рис. 1.

Рис.1. Пирамида

Чтобы доказать, что AS есть высота пирамиды, необходимо убедится в том, что AS 1 (ABC). Следуя нашим рассуждениям, нам необходимо доказать, что Z (aS, (ABC)) = 90°. Знаем, что Я 1 (ABC), то он получается Я || AS . Поэтому докажем, что z(AS, Я ) = 0, или косинус этого угла равен 1.

Расположим систему координат так, как показано на рис 2. Точка A находится в начале координат. Ось Oz будет содержать высоту пирамиды, в нашем случае AS.

Рис.2. Проекция пирамиды на плоскость хОу.

Выбрали такое положение, т.к. это облегчит дальнейшие вычисления координат необходимых точек. Поэтому получаем AS = {0; 0; VTT}. Т.к. мы указали, что основание ABC лежит в плоскости хОу, то уравнение плоскости примет вид: z = 0 и Я = {0; 0; T}. Теперь убедимся в нашем предположении:

cos(SA, Я) =

5Л-п _ 0^+0^+V1T1

= T.

Wii =   vm

Чтобы узнать угол между прямой SC и плоскостью ASB, найдем вектор нормали Я плоскости ASB.

Т.к. точки A(0; 0; 0); B(0; 4; 0); S(0; 0; VTT) E yOz,   то запишем

уравнение плоскости в виде х = 0 и Я = {T; 0; 0}.

Зная, что C(3; 4; 0), получаем SC = {3; 4; — VTT}

По нашим рассуждениям находим косинус угла

3 • 1 + 4 • 0 + (-V11) •о         3    1

cos(SC , п) =------------- ,               - = —= = -

I^2  V36  2

V12 + 0 + 0 • /з2 + 42 + (-V11)

р =

arccos- =

60°

Ответ: 60°

Задача 2. Пусть дана правильная треугольная пирамида S AB C , где S вершина и все рёбра равны 4. Точка N является серединой ребра AC, а точка Р делит высоту пирамиды в отношении 3:1, считая от точки S.

• 1)    Доказать, что прямая NP перпендикулярна прямой BS.

• 2)    Найти расстояние от точки B до плоскости, содержащую прямую NP.

Для начала построим чертеж и за точку О обозначим центр основания, тогда SO будет высотой нашей пирамиды.

Рис. 3. Треугольная пирамида

Докажем, что прямые NP 1 BS. Покажем, что их направляющие векторы перпендикулярны. Т.е. скалярное произведение данных векторов должно быть равным нулю.

Расположим систему координат так, что основание пирамиды ABC лежит на плоскости хОу, ось Oz || SO. Точку A поместим в начало координат.

Получим координаты A(0; 0; 0), C(0; 4; 0); N(0; 2; 0).

Далее, зная, что высота равностороннего треугольника определяется по формуле: h = ^-3 , в нашем случае получаем: h = BN = ^4-3 = 2-3. Из этого следует, что B(2-3;2;0). Найдем центр основания пирамиды как точку пересечения биссектрис, а в нашем случае и медиан. Медианы точкой пересечения делятся как 2:1, считая от вершины. Поэтому можем записать ON = ~ BN = 2 ^V3, тогда получаем О(^2-3; 2; 0)

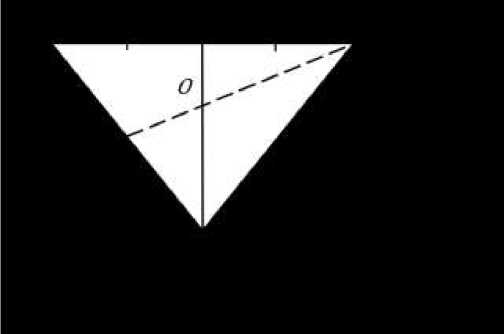
Рис. 4. Проекция треугольной пирамиды на плоскость хОу.

Точки 5 и Р при проецировании на плоскость хОу переходят в О, поэтому координаты по абцисс и ординат у них будут схожи. Найдем высоту пирамиды в прямоугольном ASOB по известной теореме Пифагора SO =

-SB2 - OB2 = JsB2 - (2bn)2 = J42 - (2 • 2-3)2 = J

16     32   4-6

^16-т = Jt = v.

2-34-6.

Тогда получаем S (——; 2 ; —). необходимо определить длину

Чтобы найти координаты точки Р,

ОР. По условию задачи, знаем что он

составляет ¹ длины высоты пирамиды SO, получаем ОР = -6. Тогда Р =

,2-3.-6.

• 3   '   ’ 3 .'

NР = { 2- ³; 0;^-6}, BS = {-^4-3; 0;^4-6}, найдем их произведение: NР •

2-3  4-3,-64-6

BS=—----— + —— = 0

• 2)    Обозначим буквой М = NP A BS. Тогда прямую NP содержит плоскость АМС . Для решения задачи воспользуемся нашей формулой, приведенной выше: р(В, (АМС)') = |^^⁰+|= | ⁺ =| = ⁺ ^ ¹

Нам необязательно находить координаты М, т.к. мы знаем координаты других точек А, Р, С G (АМС)

Cоставим систему для определения коэффициентов. Получим:

А:

Р:

С:

0 • А + 0 • В + 0 • С + D = 0 2V3 • а + 2 • в + V6 • С + D = 0;

0 • А + 4 • В + 0 • С + D = 0

{

' D = 0

V2 А = —— С

. В = 0

Подставим полученные значения в уравнение плоскости и разделим на

—2 С , чтобы избавиться от буквенного выражения

/2                           V2\

— С^х + 0^у + С^я = 0| : ( —2~С)

х — V^Z = 0

Найдем искомое расстояние р(В, (АМС)) =

I _ 2V3

= 2

Ответ: 2.

Таким образом, координатный метод является одним из рациональных методов в решении стереометрических задач. При решении задачи на нахождения расстояния геометрическим способом возникают сложности проведения самого перпендикуляра от точки до данной плоскости и применении стереометрических теорем. Традиционный способ для нахождения угла между прямой и плоскостью или прямыми требует представления и нахождения необходимого угла на чертеже. Координатный метод же позволяет без построения находить искомое расстояние и углы между плоскостью и прямыми. Данный метод будет полезен для уточнения правильности ответа решенной задачи.

Стоит отметить, что данный способ подходит не для всех типов задач. Например, в таких вопросах, где встречаются тела вращения, как конус, шар, цилиндр и т.д.