Корпусная заготовка с комплексом гидродомкратов как объект управления

Представим динамическую модель обрабатываемой корпусной заготовки как одномассовую, располагающуюся на трех упругих опорах (одна жесткий опорный элемент и два гидродомкрата) с коэффициентами жесткости С 1 , С ₂ , С ₃ и демпфирования р 1 , р ₂ и Р ₃ соответственно (рис. 1).

К обрабатываемой корпусной заготовке, приложена сила резания P ( t ) . Ее действие можно представить как P ( t ) с координатой z p [3].

Для нахождения реакций в точках установки корпусной заготовки на столе станка, представим ее в виде абсолютно жесткой рамы ABCDEF (рис. 2), находящейся в равновесии под действием системы сил – веса заготовки G заг . , резания P ( t ) , реакций опор R a , R b и R C . Причем в точке A располагается жесткий опорный элемент к которому с помощью струбцины прижата корпусная заготовка, а в точках B и C опорные элементы заменены двумя гидродомкратами, соединенными с заготовкой с помощью болтовых соединений.

Используя уравнения статики можно найти реакций опор R A , R B и R C и определить величины перемещений в точках A , B и C .

Y A

Y В

R

C

A

R В

С 2

G Заг. ₊ Р ( t ) Z p . 2 С 1 l 1 С 1 ’

=(1 + 2 G..

z_P х P ( t )     к

— )_LZ---2 ; (1)

к   С2 (к + к)

= R^ = (1 + 1G   _ z^) Pit!--l2---.

С 3            2 Заг ■     11     С 3 (12 + 13)

Величина реакций, а следовательно и пере-

мещения в точках A , B и C связано с координатой Z p приложения силы резания P ( t ) . Учитывая, что гидродомкраты предполагается установить в точках B и C корпусной заготов-

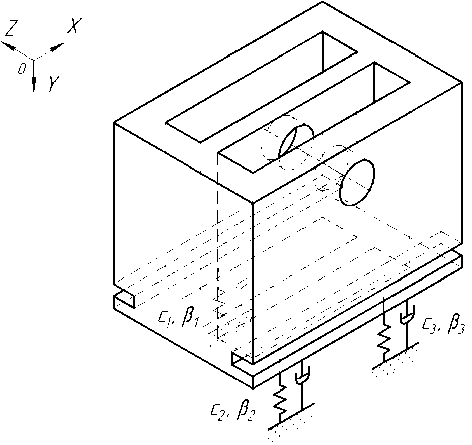
Рис. 1. Динамическая модель корпусной заготовки

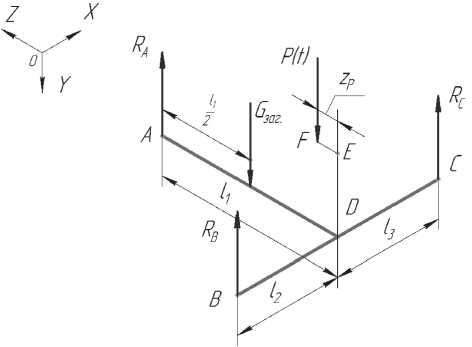
Рис. 2. К определению перемещений заготовки

в точках установки опор

мущающему воздействию точке F (рис. 3).

P f

, приложенную в

Представим перемещения отдельных точек

ки, остановимся на подробном анализе перемещений в этих точках.

Так перемещение в точке B состоит из отдельных составляющих перемещений.

Y b ( t ) = Y f + Y , ( t ) + Y 2 ( t ) + Y 3 ( t ) + Y 4 ( t ), (2) где Y f ⁽ t ), Y i ⁽ t ), Y 2 ⁽ t ), Y з ⁽ t ) и Y ₄ ( t ) - перемещения вызванные: смещением точки F контакта режущего инструмента и заготовки; контактными деформациями “основание корпусной за-готовки-опорной части гидродомкрата”; контактными деформациями “опорной части гидродомкрата-мембраны гидродомкрата”; сжимаемостью жидкости гидравлического давления из-за наличия пузырьков воздуха в системе; и контактными деформациями “основание гидро-домкрата-зеркало стола” соответственно.

Перемещение в точке С аналогично можно представить как отдельные составляющие перемещений

Y C ( t ) = Y f ( t ) + Y ₅ ( t ) + Y 6 ( t ) + Y 7 ( t ) + Y 8 ( t ), где Y ₅( t ), Y ₆( t ), Y ₇( t ) и Y 8 ( t ) перемещения вызванные: контактными деформациями “основание корпусной заготовки и опорной части гидродомкрата”; контактными деформациями “опорной части гидродомкрата и мембраны гидродомкрата”; сжимаемостью жидкости гидравлического давления; и контактными деформациями “основание гидродомкрата и зеркало стола” соответственно.

Составляющие перемещений характеризуются коэффициентами жесткости C i , демпфирования P i .

Представим корпусную заготовку с комплексом гидродомкратов как динамическую модель с приведенной массой m по отношению к воз- динамической модели как перемещения точек I…V в линейной постановки. Тогда их переме- щения можно представить следующими уравнениями:

Y(t) - Yf(t)+Yпр (t)+Y2 пр (t)+Ynp (t)+Y4 пр (t);

Y u ( t ) - Y i пр ( t ) + Y 2 пр ( t ) + Y 3 пр ( t ) + Y 4 пр ( t );

Ym ( t ) = Y 2 пр ( t ) + Y 3пр ( t ) + Y пр ( t ); (3)

Y v ( t ) = Y 3 пр ( t ) + Y 4 пр ( t );

Y v ( t ) = Y , пр ( t ) где Y i пр ( t ) = Y i ( t ) " Y_s(t );

Y 2 пр ( t ) = Y 2 ( t ) - Y ₆ ( t );

Y 3 пр ( t ) = Y 3 ( t ) - Y 7 ( t );

Y i ( t ) - Y _n ( t ) = Y f ( t );

Yu ( t ) - Y_{i n} ( t ) = Y i пр ( t );

Y_in ( t ) - Y v ( t ) = Y _? пр ( t );

Y v ( t ) - Y v ( t ) = Y 3пр ( t ); Y v ( t ) = Y 4 пр ( t ).

Следует отметить, что выбор точки F , относительно которой записываются все уравнения движения, не случаен. Это можно объяснить тем, что решение основной задачи стабилизации осей растачиваемых отверстий и инструмента наиболее эффективно достигается когда гидродомкрат устанавливается в точках B и C базирования корпусной заготовки, а точкой приведения является точка F . Это упрощает написание уравнений движения.

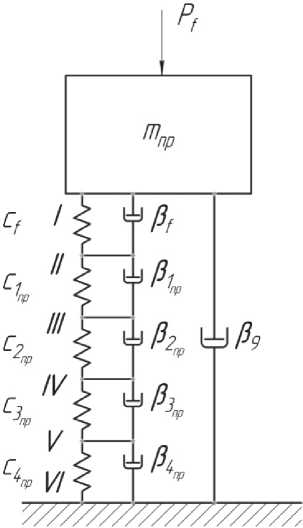
Рис. 3. Динамическая модель обрабатываемой корпусной заготовки с комплексом гидродомкратов

Перемещение точки D корпусной заготовки можно описать системой дифференциальных уравнений pt)=тпр dY+C y-Y-)f (dY- dY)+a dY;

C(V V\ R( i ПХ — П (V V\a_R ( И и±Ш\.

^{Cf(Y -y}") ^{+ P f (} dt dt ) = C пр (Y I Y¹¹ ) ⁴ пр ⁽ dt dt ^);

dY dY              dY dY dYII dYIII                      dYIII dYIV

⁴пр ⁽ I I, ) ^p пр ⁽ dt    dt )     пр ⁽ '” ^IV ) ^Р пр ⁽ dt dt ^); (4)

dY dY              dY dY

C 2 пр (Y ,,, - Y v ) + А пр ( dY - df ) = C пр (Y v - Y ) + А пр ( dY - dY );

dt   dt                     dt dt dY dY          dY

C (Y_y - y ) + А ( dY - dY ) = C У + А dY .

3пр ( . V) pпр ( dt dt ) 4п V Рпр dt где C 1 пр , С 2 пр , С 3 пр , С 4 пр – приведенные коэффициенты жесткости в стыках “основание корпусной заготовки-опорной части гидродомкрата”, “опорной части гидродомкрата-мембраны гидродомкрата”, сжимаемости жидкости гидравлического давления и в зоне контакта “основание гидродомкрата-зеркало стола” соответственно.

^p i пр , ^Р 2 пр , ^Р 3 пр , ^Р 4 пр — “основание корпусной заготовки-опорной части гидродомкрата”, “опорной части гидродомкрата-мембраны гидродомкрата”, сжимаемости жидкости гидравлического давления и в зоне контакта “основание гидродомкрата-зеркало стола” и гидродомкрата соответственно.

Составим систему уравнений (4) в операторной форме.

P s ) - т пр ⁽ Y_f+ Y i пр + У пр + Y 3 пр + У пр ⁾ s ² -           '

А ⁽ Y f + Y i пр + Y пр + Y 3 пр + Y пр ⁾ s = -^ f + 1 ⁾ Y f ⁽ s ⁾ ;

C f

p ( s ) - m ( y_f + Y + Y + Y + Y ) s ² - пр f     1 пр     2 пр 3 пр     4 пр

Р 9 ( Y f + Y i пр + Y пр + У з пр + Y 4 пр ) s = -¥ - ( T_x s + 1 ) } ; пр ( s ) ;

C ¹ пр

P ⁽ s ⁾- т пр ⁽ Y f + Y i пр + Y 2 пр + У з пр + Y 4 пр ⁾ s ² -

А ( у, + Y + У + Y + У ) s = 9 f 1 пр     2 пр     3 пр     4 пр

,.' T s + 1 } пр ( s ) ; [ ⁽⁵⁾

C ₂

2 пр

Ps ) - m Y + Y + Y, + Y + Y ) s ² - пр f 1 пр     2 пр     3 пр     4 пр

А Y + Y + Y + Y + Y ) s =—( Ts + 1 ) y ( s ) 9 f 1 пр     2 пр     3 пр     4 пр                 3         3 пр

C 3 пр

P ( s ) - т пр } + Y i пр + У пр + Y 3 пр + У пр >² -

Р 9 У + У пр + Y пр + } пр + Y пр ) s = -1- T s + 1 ) } пр ( s ) C 4 пр

На основании системы уравнений (5) можно построить структурную схему объекта управления корпусной заготовки с комплексом гидродомкратов по отношению к возмущающему воздействию P ( t ) .

Выходной управляемой величиной следует принять вертикальное перемещение точки F , в которой приложена сила резания P ( t ) .

У вых ( t ) = Y f ( t ) + Y i пр ( t ) + Y 2 пр ( t ) + Y 3 пр ( t ) + Y 4 пр ( t ).

Найдем передаточную функцию объекта, найдем на основании структуры, изображенной на рис. 4.

W

^{( s} ) =

Y ( s )

вых X / _

P f ( s ) "

возм

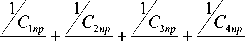
Ts +1 T ₂ s +1 T ₃ s +1 T 4 s +1

i+

1/     1/     1/      1/      1/

/с   /с   /с    /с

/ C f ₊ / C i пр ₊ / C 2 пр ₊ / C 3 пр ₊ / C 4 пр T f- s +1 Ts +1 T ₂ s +1 T ₃ s +1 T 4 s +1

^{( p} 9 ^{s + m}пр^{s 2 )}

Выполнив необходимые преобразования выражение (6) можно представить в виде как

W

возм

( s ) =

У вых ( s ) = P f ( s )

А _f ( T_fs + 1 )[ t ₃ ³ _fs ³ + T ₂ ² _fs ² + T _{1 f}s + 1 ]

T 85 f s ⁵ + T ₇ ⁴ f s ⁴ + T 6 ³ f s ³ + T 5 ² f s ² + T 4 f s + 1

где Р _f

—¹ + —¹ + —¹— + —¹— - коэффи-c. C, C,       c ,

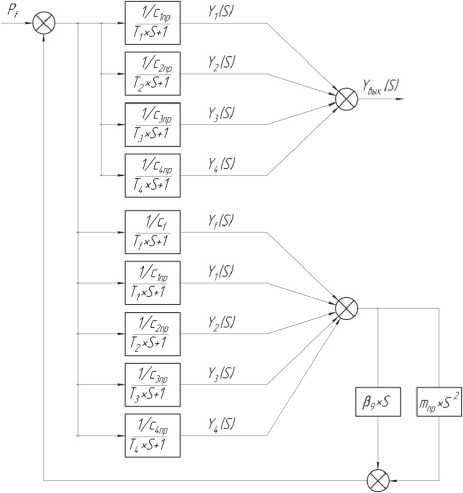
Рис. 4. Структурная схема объекта управления с комплексом гидродомкратов по отношению к возмущающему воздействию

( dYvi_L_dY_L \

F ra ⁽ t ) C 9 W, Y , ^{) + p} 9 I ,

V dt dt )

c 9 V , - ¥ ,

d 2 Y ,

= m*p     + dt

, _x „ f dY , dY, Л „ ^C f ^{( Y} , ^{- Y} ,, ) ^{+ P} f I      ^-—T" I ^{+ P} 9*

V dt dt )

C f (y - y ,,) ₊ p f [ dY - ^dY A+ p_y dY = c , n _P (y , V dt dt ) dt

C (y -Y }+ Й fdYL-dYL) = c (y пр I, L in T^" р1 пр                               2 пр\‘,,, dt dt

V

in.

( d¥ ,, d¥ ,,, ). ^{)+ Р п}р V dt dt у

f dY , ^d¥ „ A

^{)+ p} 2пр I                    I ;

V dt dt у

C (Y -Y Ar0 ^f dYLL-dlvL K_C (y -yVB ^fdY V ^d1V \

2 пр ^{( 1} II, ¹ V ) ^{+ P} 2 пр I dt dt I     ³ пр ^{( 1} I Y ' ^ ^P пр I dt dt У

C 3 пр ( Y V

-Y V В ^f dYV - dYV 1=C Y+B

Y V ^{) + P} 3пр I dt dt I С ⁴ n^{p I} V ^{+ P} пр

dYV dt

;

dY , _;

dt

В операторной форме эта система принимает вид

F ra ^{( s )} = ^C 5 T ra s ⁺ Y ^{( s} ^

^{F (} s ) ^{- т}пр ^{[ 1}f ⁽ s ) ^{+ Y (} s ) ^{+ Y} 2 ⁽ s ) ^{+ Y}3 ⁽ s ^{) + Y} 4 ⁽ s )k ^{2 -}

- A Y , ( s ) + ¥ ( s ) + ¥ 2 ( s ) + ¥ з ( s ) + ¥ 4 ( s ) ] s = C f f + 1 ) 1 f ( s ) ;

^{F ( s ) - т}пр ^[ Y f ^{( s} ) ^{+ Y ( s ) +} Y 2 ^{( s ) + Y ( s ) +} Y 4 ^{( s )]} s ^{2 -} - A .\Y f ( s ) + 1 1 ( s ) + ¥ 2 ( s ) + ¥ з ( s ) + ¥ 4 ( s ) ] s = C 1 пр (T_x s + 1 )i ; ( s ) ;

Fra (s)-тпр [Yf(s ) + y(s) + Y2(s) + Y3(s) + Y4(s )]s2 -

При использовании в системе автоматической стабилизации двух гидродомкратов в уравнение движения вместо коэффициента демпфирования необходимо ввести значение приведенного коэффициента P ₉ * = P 9 + P 9пр , учитывающего действие обоих домкратов.

При рассмотрении объекта по отношению к управляющему воздействию в качестве управляющего воздействия принимаем усилие развиваемое гидродомкратом. Представим динамическую модель объекта регулирования (обрабатываемой корпусной заготовки) при действии силы F ГД , развиваемой гидродомкратом (рис. 5).

Найдем дифференциальные уравнения движения точки F обрабатываемой корпусной за-

- P _s .\ Y f ( s ) + 1 1 ( s ) + ¥ 2 ( s ) + ¥ з ( s ) + ¥ 4 ( s ) ] s = C 2 пр ( T 2 s + 1 ) 1 2 ( s ) ;

^Fra ^{( s ) - т}пр ^[ Y f ^{( s} ) ^{+ Y ( s ) +} Y 2 ^{( s ) + Y ( s ) +} Y 4 ^{( s )]} s ^{2 -} - pPy ( s ) + 1 1 ( s ) + ¥ 2 ( s ) + ¥ з ( s ) + ¥ 4 ( s ) ] s = C 3 пр ( Т з s + 1 ) ¥ з ( s ) ;

^Fra ^{( s ) - т}пр ^[ Y f ^{( s} ) ^{+ Y ( s ) +} Y 2 ^{( s ) + Y ( s ) +} Y 4 ^{( s )]} s ^{2 -} - A .\Y f ( s ) + 1 1 ( s ) + ¥ 2 ( s ) + ¥ з ( s ) + ¥ 4 ( s ) ] s = C 4 пр ( T 4 s + 1 ) 1 4 ( s ).

готовки.

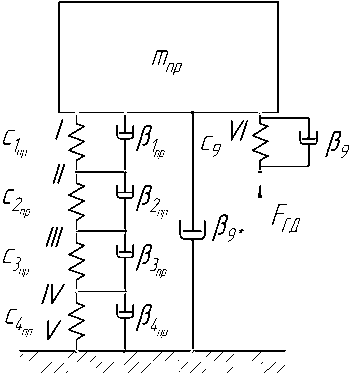
Рис. 5. Динамическая модель объекта регулирования при действии силs F _ГД , развиваемой гидродомкратом

На основании системы уравнений (9) можно построить структурную схему объекта управления корпусной заготовки с комплексом гидродомкратов по отношению к управляющего воздействия силы F ГД , создаваемой гидродомкратом (рис. 6).

Передаточная функция упругой системы объекта по отношению к управляющему воздействию силы P ГД , создаваемой гидродомкратом имеет вид:

W yc ( s ) =

Y v ( s )

F гд (s )

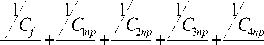
T f s + 1 T 1 s + 1 T ₂ s + 1 T 3 s + 1 T 4 s + 1

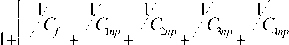
Tf3 + 1 Ts + 1 T 2 s + 1 T 3 s + 1 T₄s + 1

( ^p ₎ ^{s +} т, р ? 2 )

+

T ra s + ¹

где Y v ( s ) — перемещение V точки в операторной форме.

Выполнив необходимые преобразования выражение (10) можно представить в виде как

W yc ( s ) =

YV (s ) FГД (s )

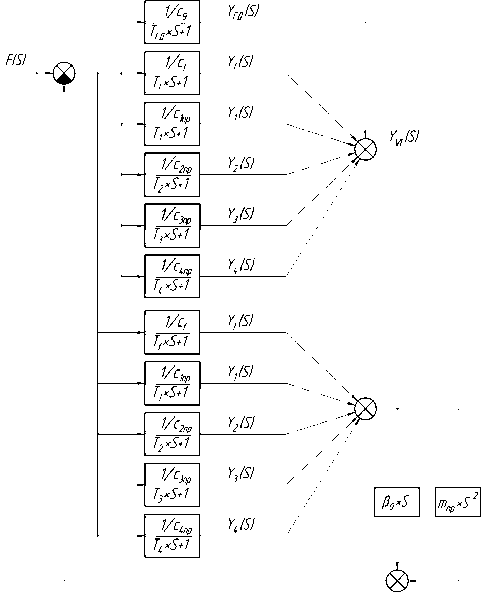
Рис. 6. Структурная схема объекта управления корпусной заготовки с комплексом гидродомкратов при действии силы F ГД

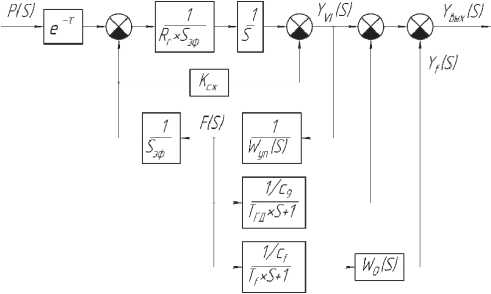
Рис. 7. Структурная схема каналов по управлению

R ТР – сопротивление трубопроводов;

S ЭФ – эффективная площадь мембраны [4].

Структурная схема одного канала объекта по отношению к управляющему воздействию представлена на рис. 7.

W s ) =

x7-----

1 +

/ f + / ¹ пр + / пт + / пр + / при T f s + 1 T^s + 1 T₂s + 1 T₃s + 1 T₄s + 1

Преобразуя выражение (13) получим

W 0 ( s ) =

— [ T4_f s ⁴ + T³ s ³ + T² s ² + T ,s + 1] ^{4 f         3 f         2 f         1} f

C

T ₄ ⁴ s ⁴ + T ₃ ³ s ³ + T ₂ ² s ² + T 1** s + 1

T ₄ ⁴ s ⁴ + T ₃ ³ s ³ + T₂*² s ² + T 1* s + 1 ’

^(Tгд^{s +} 1)

B _f (t^ s + l^ Y s ⁴ + T ₃ ³ Y s ³ + T ₂ ² Y s ² + T_{1 Y} s +

__**      __ __ __ __ __*      __*

где ^T 1 = T 1 ⁺ Т 2 ⁺ Т 3 ⁺ Т 4 ’ ^T 5 = ^T 5 У •

Тогда можно найти передаточную функцию объекта по управлению

T f s ⁴ + T f S ³

+ T ^ ²jS² + T f s +

•

W y ( s )

Y вых ^{( s )} =

P ( s )

Здесь В , = ----+----+----+---- - ко- fC C C C

1 пр 2 пр 3 пр 4 пр эффициент передачи.

На основании методики [2], найдем уравнения движения объекта по отношению к управляющему воздействию – давлению рабочей жидкости, подаваемой в гидродомкрат:

11    1

• ‘

^Rr ^Sэф ^{s 1 +} K c • ^S„ 1W- C ( s )

1 ₊ 1     1 ___________1__ 1

⁺ Rr ^S„ 's '1 + Kc . S„ 1W_{ic ( s} )' S„ '«V ⁽ s )

Y v ( s ) =

1 Р ( s ) e ^{- r s} - P ГД ( s ) ------------------------- • ----------------------------------------------------------------------------------------

S эф s R Г

X

1 +

1/

1        /С 9

--------------7----7" • ----------------------- W ус ( s ⁾   T ГД s + 1

1 C f

T_fs + 1

• « 0 ( s )

W yc ( s )

Y v ( s ) _; F ГД ^{( s )}

вы ( s ) = Y 1 ( s ) + Y 2 ( s ) + Y 3 ( s ) + Y 4 ( s ) = У гд ( s ) + Y f ( s )•

Здесь P ГД – давление рабочей жидкости в гидродомкрате [2];

РГ = Rrp + RTp - суммарное гидравлическое сопротивление, где RГР – сопротивление гидропреобразователя;

где « ус ( s ) – передаточная функция упругой системы, определяемая из выражения (11).

На рис. 8 представлена структурная схема объекта с учетом его многосвязности.

Таким образом, найденные аналитические выражения (7), (11) и (15) позволяют найти передаточных функций корпусной заготовки с комплексом гидродомкратов по отношению к управляющему и возмущающему воздействиям.

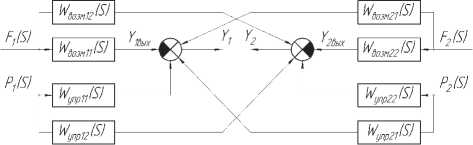
Рис. 8. Структурная схема объекта с учетом многосвязности