Коррекция пространственных потерь в телевизионной системе регистрации, работающей в особых условиях

Различные задачи производственного и исследовательского характера на предприятиях, использующих радиоактивные материалы, решаются в радиационно-защитных камерах. Учитывая высокую ответственность, а зачастую и уникальность выполняемых работ, все технологические операции документируются с целью дальнейшего анализа. Для этой цели используются телевизионные системы регистрации (ТВ-системы), которые располагают перед смотровой системой в зоне, защищенной от радиации, как показано на рис. 1.

Рис. 1. Функциональная схема системы регистрации

Особые условия, которые обусловлены наличием смотровой системы толщиной несколько сотен миллиметров между объектом и камерным объективом, вносят специфику в формирование изображений такой ТВ-системой. Автором выполнен анализ ТВ-системы, при котором тракт формирования и передачи информации представлялся состоящим из ряда преобразовательных и усилительных звеньев, как показано на рис. 2.

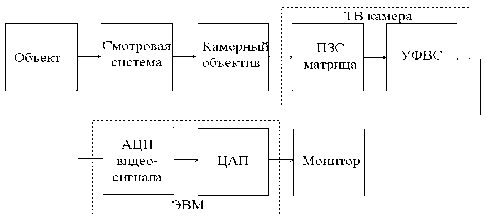
Рис. 2. Представление ТВ-системы для анализа

Ограниченные пространственные разрешающие способности смотровой системы, камерного объектива, ПЗС камеры и воспроизводящего монитора не позволяют регистрировать мелкие детали изображения с достаточным числом градаций, а начиная с некоторых пространственных частот эти детали вообще перестанут регистрироваться системой. Эти ограничения описываются относительной двумерной частотноградационной характеристикой системы (ЧГХ) [1], которая определяется отношением числа градаций т_э (Q) , различимых на пространственной частоте Q, к числу градаций т_ю ' различимых на пространственной частоте, близкой к нулю: 5_Твс^ = »Ъ(Р)/™о_Э • ЧГХ является убывающей функцией пространственной частоты (см. рис. 3):

З_твс (Q) = 1, при Q = 0;

1 >  5_ТВС (Q) > 0, при Q > 0.

Если в целях упрощения предположить, что число градаций различимых на экране монитора ЭВМ в крупных деталях 7ИОЭ и относительная ЧГХ 5ТВ с (^) не изменяются по полю изображения и воспользоваться их усредненными значе- ниями ^оз и 5ТЙС(П), то количество информации на выходе ТВ-системы, снимаемое с экрана монитора, будет определяться выражением [1]

Np

^ тш ⁼ ^ Jl®g2[^w^0 3^<^rac(^) "*~ Ц^^ ⁼ о

= 3^1og2w03 + 3 jlog2[Jrac(Q) + l/m03]c7Q, где N – число элементов разложения в растре;

Q – двумерная пространственная частота.

Второе слагаемое в этом выражении определяет пространственные потери и при тоэ ^ 1 является отрицательным.

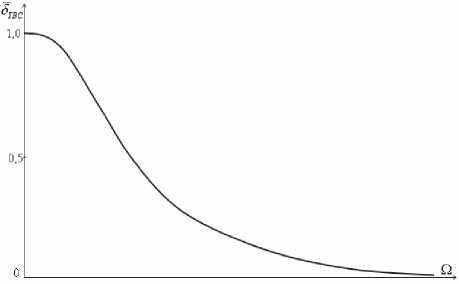
Рис. 3. Относительная ЧГХ системы регистрации

Выполненный анализ ТВ-системы показал, что с дос т аточной для практики точностью зависимость 5_твсЛС1) можно заменить двумерной частотноконтрастной характеристикой T(N_x,N_v) , которую можно построить инструментальными средствами. Несмотря на то что ЧКХ не учитывает зависимость числа воспроизводимых градаций от шумов, она позволяет проследить за качественными изменениями пространственных потерь.

Возникающие в ТВ-системе пространственные потери можно разделить на две следующие группы.

• 1.    Потери, вызванные хроматическими аберрациями в смотровой системе (хроматизм положения и хроматизм увеличения). Такие потери приводят к ухудшению различимости мелких деталей изображения и цветовым искажениям. Причины их возникновения и предлагаемый метод коррекции рассмотрены автором в [2].

• 2.    Потери, вызванные монохроматическими аберрациями (сферическая аберрация, кома, астигматизм), а также неидеальными частотными характеристиками преобразовательных и усилительных звеньев. Они приводят к снижению пространственной разрешающей способности

системы и выражаются в ухудшении различимости мелких деталей изображения или их полной потере. Однако если мелкие детали потеряны не полностью, то их передачу можно улучшить, используя методы коррекции и улучшения изображений.

Коррекция частотно-контрастной характеристики

Целью коррекции ЧКХ является такая коррекция характеристик системы, которая позволяет получить на выходе изображение, соответствующее идеальной системе. Если характеристики объектива, ТВ-камеры и монитора выбраны высокоразрешающими, то в качестве «идеальной» можно рассматривать систему регистрации, в которой отсутствует звено радиационно-защитной смотровой системы, вносящее максимальный вклад в потери пространственной информации. Будем считать такую систему эталонной. Структура эталонной системы показана на рис. 4а). Структура реальной системы регистрации отличается от эталонной наличием между объектом и камерным объективом смотровой системы и показана на рис. 4б).

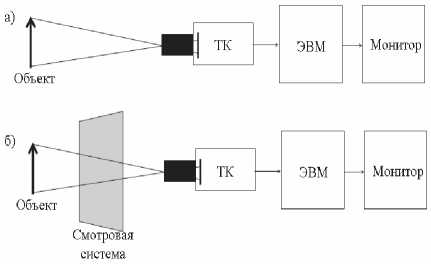
Рис. 4. Структура ТВ-систем регистрации а) эталонной; б) реальной

Несмотря на наличие аберраций комы, и астигматизма, которые делают систему регистрации неизопланарной в целом, поле изображения можно разбить на зоны, в пределах которых условия изопланарности будут соблюдаться с определенной точностью [3]. Поэтому в первом приближении такие системы регистрации можно считать линейными, инвариантными к сдвигу и рассматривать их как линейные двумерные фильтры пространственных частот.

Процесс образования изображения в этом случае можно описать математической зависимостью между характеристиками объекта, системы регистрации и получаемого изображения. Для области пространст в енных частот можно записать [4-5]

EVNx,Nt) = H(Nx,Nv>UNx,Nv)’ (!)

где                                           – двумерный спектр распределения яркостей в плоскости изображений;

L(N_x,N_y) = J Y^yV^’^^dxdy – двумерный спектр распределения яркостей в плоскости объекта; HtN^NJ – двумерная передаточная функция системы регистрации; N_x, N_v

– пространственные частоты по направлениям X и у в плоскостях изображений и объекта.

Известно, что передаточная функция

H(NX,NV) является преобразованием Фурье реакции системы на входное воздействие Жу1) в виде двумерной 6 -функции. Следовательно, ее можно представить в виде

H{Nx,Ny-)=Y\H(x,yV Лп(^хХ+г'уУ>>dxdy .

Выполнив преобразование этого выражения с помощью формулы Эйлера e ' = cos rax - i sin cox, где 1"N , представим передаточную функцию в виде вещественной и мнимой частей:

H(Nx,Ny) =

J Jя(x ,y )cos2;r(^.x + N_vy )dx dy -

-J |я(х ,y )sin2^(^x + N_vy yixdy =

= ReH(N_x,N_v) + 1шЯ(Я_л,Я_г).

Используя (2), запишем передаточную функцию в виде модуля T(N_x,N_x3 и аргумента ^,N_y), которые зависят от пространственных частот N_x,N_y и представляют собой двумерные амплитудно-частотную и фазо-частотную характеристики вида

H(Nx,Ny)^\H(Nx,Ny)\e^+^

= T(Nx,Ny)e'l’(Ny+Nr\

При этом

T(N_x, N_y) = ^eH(N_x, N_v )]² + [1шЯ(Я_г, Я_г )]² ;

1тЯ(Я_л,Я_г) ReH(N_x,Nj

В большинстве случаев импульсный отклик системы H(x,y)симметричен по направлениям x и y, следовательно, является четной функцией. Поэтому второй интеграл в выражении (2) будет равен нулю, а передаточная функция H(Nx,Ny) будет являться вещественной и характеризовать пространственный фильтр с нулевым сдвигом фазы. Модуль этой двумерной функции \H(Nx,Ny)\ является двумерной частотно-контрастной характеристикой системы и позволяет установить соответствие между двумерными спектрами распределения яркостей в объекте и его изображении

T(N_x,N_y) = \H(N_x,N_y)\.           (3)

Исходя из изложенного, для эталонной и реальной систем регистрации, показанных на рис. 4, запишем

E_ (N_x, N_y) = \H_ (N_x , N_y )| • Lx, N_y ); (4)

Ё_Р(К_ХЛ>\НДМ_ХЛД-^ (5)

Если целью коррекции считать получение на выходе реальной системы изображения, совпадающего с изображением на выходе эталонной:

E3„(N.x,Ny) = Ep(Nx,Ny), то ЧКХ реальной системы следует умножить на некоторую двумерную корректирующую функцию \ЙК(ЯЛД таким образом, чтобы это равенство выполнялось:

\H_P (N_x , N_y )|\H_K (N_x , N_y )| L(N_x ,N_v) =

= \^(Nx,Ny)\-L(Nx,Ny).

После несложных преобразований получим

\H^Nx,Ny)\

|Я_(Л^Я^ \н_Р^_хл_у)\

TJ,„(Nx,Ny') T(Nx,Ny)

Поскольку в анализируемой системе регистрации шумовая составляющая очень мала, задача коррекции сводится к отысканию линейного корректирующего фильтра с передаточной функцией, определяемой выражением (6). Такой фильтр включается в систему регистрации как отдельное звено и называется обратным фильтром. Обобщенный алгоритм такого способа коррекции предполагает получение Фурье-образа исходного изображения, его преобразования с помощью фильтра с необходимой передаточной функцией и последующего обращения результата для получения обработанного изображения [4-5]. Коррекцию следует выполнить до синтеза изображения на экране монитора. В то же время логично вклю- чить ее в ту часть системы регистрации, где полученные изображения объекта будут оцифрованы и храниться в памяти в виде массивов удобных для выполнения операций, предусмотренных алгоритмом.

Поскольку в анализируемой системе используется цветная ТВ-камера, изображение объекта наблюдения, после ввода его в ЭВМ будет храниться в памяти в виде полноцветного RGB-изображения. Такое оцифрованное изображение представляет собой трехмерный массив, фактически состоящий из трех прямоугольных матриц размером MxN , каждая из которых содержит индексированные переменные со значениями, соответствующими относительной яркости красного R, зеленого G и синего B цветов. Элемент массива Кг,сЛ определяется значениями индексов, где r и c – номер строки и столбца, которые задают положение пиксела, n – номер матрицы, задает доступ к матрице нужного цвета. Введем обозначения:

[7(r,c,l)] = [B(r,c)] = R - матрица красной составляющей;

" 7?(0,0)     8(0,1) . . . 7?(0Л-1)    "

/?(1,0)      7?(1,1)   . . . 8(1, TV-Г)

прямое двумерное дискретное преобразование Фурье (ДПФ). Например, для красной составляющей изображения можно записать

1 М-1 N-1             ,,

5л^гл.а=—'Е£в('^ж уГ^лС • (7>

,.=0 с=0

Поскольку комплексное ядро этого преобразования разделимо

^(Nv,Nx.;r,c) = C ^vC ;

Г 2тг

W, = ехр Ч— , N е{0,1,...Л7-1} ;

( 2л\

W, =ехр -z— ,7V e{0,l,...7V-l}, -        ( TV J и удовлетворяет условию ортогональности [5], выражение (7) можно записать в следующей матричной форме

SR=AcRAr,

где Sr – матрица спектральных коэффициентов ДПФ для R-компоненты; R – матрица значений R-компоненты изображения;

A_c – матрица преобразования размером MxM:

R(M-X,0) R(M- 1,1) . . .R(M-1,N-^

[/(/',с,2)] = [G(r,c)J = G - матрица зеленой составляющей;

o (

W] Wj

_w2(M-n _wGW-l)(M-l)

G(0,0) G(l,0)

G(0,l) . . . С(0Л-1)

G(l,l) . . . С(1Л-1)

A_r – матрица преобразования размером NxN:

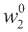
С(М-Ш G(M-U) . . .С(М-1Л-1)

[7(r,c,3)] = [8(r,c)] = B — матрица синей составляющей;

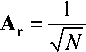
0     12

W2 W2

0    24

w2 w2w

w^"-^

0     (.

^2 W2

2(N-\A

W2

. ,w2

8(0,0) 8(1,0)

8(0,1) . . . В(0Л-1) 8(1,1) . . . 8(1Л-1)

В =

В(М -1,0) В(М-1,1) . . .В(М-1Л-Й г = о;1;2... м-\ – номер строки матрицы; с = о;1;2... TV-1 – номер столбца матрицы; М – число отсчетов цифрового изображения по вертикали (поперек строк); N – число отсчетов цифрового изображения по горизонтали (вдоль строк).

Для перехода в частотную область к каждой компоненте изображения следует применить

Таким образом, матрица спектральных коэффициентов двумерного ДПФ для красной компоненты RGB изображения Sr получается как результат последовательного выполнения двух одномерных ДПФ: сначала выполняется одномерное преобразование по всем столбцам матрицы отсчетов R (умножение на матрицу A слева), затем выполняется второе одномерное преобразование по всем строкам полученной матрицы (умножение на матрицу Ar справа). Размер матрицы получившихся коэффициентов совпадает с размером матрицы исходного изображения R и равен MxN. Аналогичные матрицы отсчетов двумерного ДПФ получаются для зеленой G :

SG = Ac G Ar и синей В:

SB = Ac В Ar компонент полноцветного изображения.

Поскольку матрица ядра ДПФ симметрична по отношению к ее главной диагонали, матрицы преобразования по столбцам A и строкам Ar являются унитарными и по определению

A;¹ =a;^t=a_c;

A>A7=Ar.

Действительные унитарные матрицы являются ортогональными и для них справедливы соотношения

a;1=act=ac;

A;,=Aj=Ar.

Отсюда следует, что обратный переход от частотного представления к пространственному можно представить в виде матричных выражений

R = AC SR Ar;

G = AcSGAr;             (9)

B = AC SB Ar.

Практическая реализация и результаты эксперимента

Как следует из выражения (6), для вычисления передаточной функции корректирующего фильтра следует знать двумерные ЧКХ эталонной и реальной систем. Различие методов измерения ЧКХ связано в первую очередь с различием используемых для этой цели тест-объектов. В [6] автором изложен метод вычисления ЧКХ с использованием тестового изображения шумового поля.

Следуя изложенным в [6] принципам, вычислим частотно-контрастные характеристики эталонной и реальной систем регистрации. Для этого оцифруем и введем в память ЭВМ эталонное тестовое изображение шумового поля, зарегистрированное без смотровой системы (см. рис. 5).

Рис. 5. Эталонное изображение тестового шумового поля размером 512×512

Получим трехмерный массив полноцветного эталонного изображения V-.^bc,^"^, состоящий из трех прямоугольных матриц ^"м/эт ’ ^гиэт ’ ^waw * Как показали экспериментальные исследования, частотно-контрастные характеристики для красного, зеленого и синего каналов практически совпадают. Это позволяет минимизировать вычисления и использовать общую ЧКХ, рассчитанную по любой из компонент изображения шумового поля, например по красной ^^ Л, 3fj[ "

Вычислим ЧКХ эталонной системы регистрации в вертикальном направлении (поперек строк), выполняя следующие шаги:

• -    выполним одномерное ДПФ по всем столбцам матрицы ^ ui эт в соответствии с (8):

S = A R ^ш зтс зт ’ полученная матрица спектральных коэффициентов будет иметь размер MxN и в общем случае состоит из комплексных значений. Для перехода к вещественным значениям вычислим модули спектральных коэффициентов и получим матрицу |^шэтс | ’

• -    полученную матрицу модулей спектральных коэффициентов | ^ UI эт c | можно рассматривать как совокупность из N векторов-столбцов размером Mx;-. 8_шэ„_нЛс), где c = O;l... A-l – номер столбца матрицы. Каждый вектор-столбец представляет собой спектральное распределение реализации соответствующего столбца шумового поля.

Вычислим усредненный спектр шумового поля в вертикальном направлении. Для этого выполним усреднение по всем столбцам

SIIOIK ^Хж O') ’ c=0

полученный вектор-столбец будет соответствовать двум полупериодам ЧКХ эталонной системы регистрации в вертикальном направлении T,_m(NJ-

Аналогичные действия выполним для вычисления ЧКХ по горизонтали:

- выполним одномерное ДПФ по всем строкам матрицы ^шэп? в соответствии с (8):

перейдем от комплексных значений к вещественным и получим матрицу Is I ’

- рассматривая матрицу модулей спектральных коэффициентов как совокупность из М векторов-строк размером IxW: s„„„„.(r), где r = O;l ...M-\ – номер строки матрицы, выполним усреднение спектра по всем строкам шумового поля:

i A/—1

S =---\ ' е (r\ шэтг 4  / 4 шэтг X / ?

полученный вектор-строка ^ш эт г соответствует двум полупериодам ЧКХ эталонной системы регистрации по горизонтали TJNJ. Отметим, что вычисление ЧКХ эталонной системы можно выполнить заранее на этапе калибровки.

Рис. 6. Реальное изображение тестового шумового поля размером 512×512

Для вычисления ЧКХ реальной системы регистрации оцифруем и введем в память ЭВМ тестовое изображение шумового поля, зарегистрированное в реальных условиях (см. рис. 6).

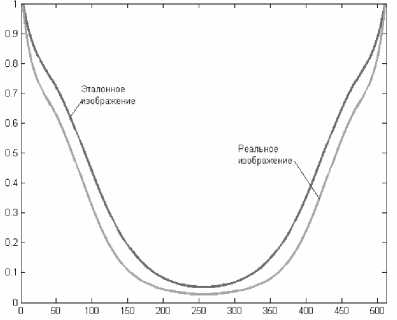
Рис. 7. ЧКХ эталонной и реальной систем регистрации в вертикальном направлении

Рассматривая трехмерный массив тестового изображения [4(^г,^^и)] , состоящий из трех матриц К_и, G,„, В„,, и выполняя описанную выше последовательность действий над любой из них, например над R^ , получим вектор-столбец S_wc и вектор-строку S_{to r} , которые соответствуют двум полупериодам ЧКХ реальной системы регистрации в вертикальном T_p ( N_v) и в горизонтальном T„(N_X) направлениях. Вид полученных нормированных и сглаженных характеристик показан на рис. 7-8.

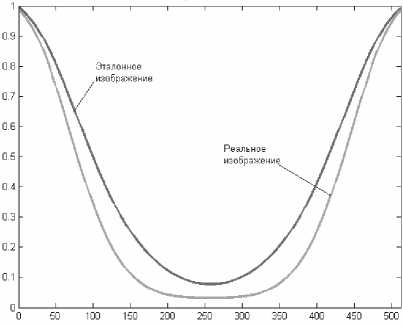
Рис. 8. ЧКХ эталонной и реальной систем регистрации в горизонтальном направлении

От одномерных ЧКХ легко перейти к двумерным характеристикам, если найти матричное произведение

T             ¥ =T • эт \ x ’ у / ги эт с ш эт г эт ’

T/N^NJ^-Xc^p.

Вид этих характеристик показан на рис. 9-10.

Для вычисления передаточной функции корректирующего фильтра в соответствии с полученным ранее выражением (6) следует выполнить деление ЧКХ эталонной системы на ЧКХ реальной системы для каждой пространственной частоты. Известно, что операция деления матриц в общем случае не определена. Однако в нашем случае получившиеся матрицы можно рассматривать как упорядоченный набор данных, идентифицируемый с помощью индексов, то есть как массивы данных.

Рис.9. Двумерная ЧКХ эталонной системы

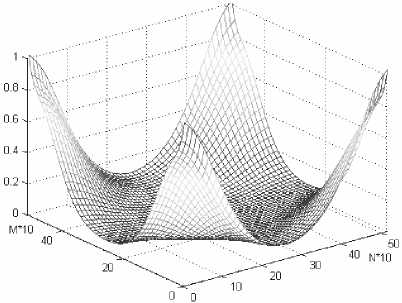
Рис. 10. Двумерная ЧКХ реальной системы

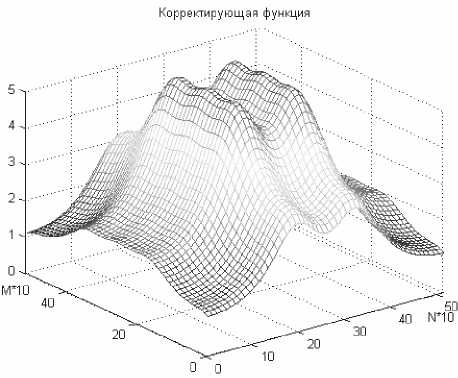
Рис.11. Двумерная передаточная функция корректирующего фильтра

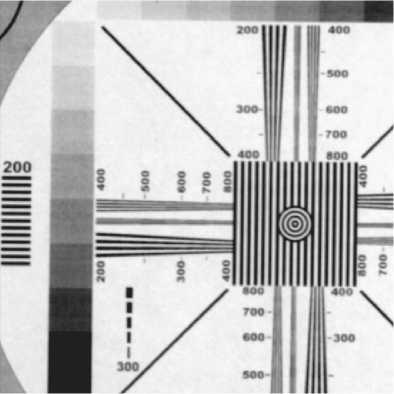
Рис.12. Изображение тестовой таблицы до фильтрации

Для массивов одинаковых размеров существует операция поэлементного деления • / и поэлементного умножения . * , которые и следует использовать в подобных случаях. Таким образом, получим htc = V,' / $шг ihAr = s„,,„„. • / s„m„r; II = T„„ ■ /Tp , где htc и htr – корректирующие функции по вертикали и по горизонтали, а H^. – двумерная передаточная функция корректирующего фильтра, показанная на рис. 11.

После того как передаточная функция корректирующего фильтра сформирована, остается выполнить собственно коррекцию исходного изображения, например такого, как показано на рис. 12. Видно, что изображение слегка размыто из-за влияния монохроматических аберраций.

Проведем коррекцию в следующей последовательности:

• -    выполним ДПФ каждой цветовой компоненты исходного изображения в соответствии с (8) и получим три матрицы спектральных коэффициентов S_R , S_G и S_B ;

• -    выполним поэлементное умножение полученных матриц на матрицу двумерной передаточной функции корректирующего фильтра и получим три матрицы скорректированных спектральных коэффициентов

SR=SR-*H,; SG=SG.*H,; SB=SB.*Ht;

• -    для перехода в пространственную область над полученными матрицами выполним обратное ДПФ в соответствии с (9) и объединим полученные R , G , В компоненты в цветное скорректированное изображение, которое показано на рис. 13.

Заключение

Рассмотренный метод коррекции монохроматических аберраций оказался достаточно эффективным для анализируемой системы регистрации. Однако если в данной системе шумы практически не оказывают влияние на изображение, то в системах с высоким уровнем шумов результаты будут отличаться от приведенных. Это является известным недостатком обратной фильтрации. Из-за ограниченного объема в статье не рассмотрены вопросы дополнения матриц спектральных коэффициентов нулями, что необходимо выполнять с целью избавления от краевых искажений [4].

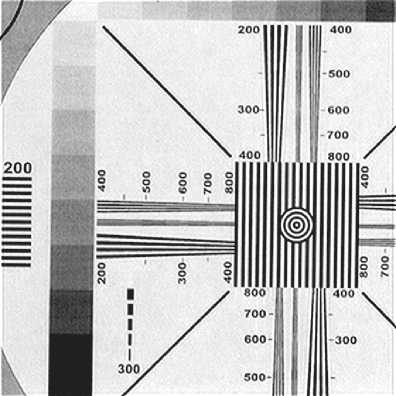
Рис. 13. Изображение тестовой таблицы после обработки фильтром

Рассмотренную коррекцию можно выполнить и в пространственной области, если по вычисленной передаточной характеристике корректирующего фильтра синтезировать соответствующий пространственный фильтр[4].