Корректность задач Дирихле и Пуанкаре в цилиндрической области для многомерного уравнения Чаплыгина
Автор: Алдашев Серик Аймурзаевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.15, 2013 года.
Бесплатный доступ
В работе показано, что задачи Дирихле и Пуанкаре в цилиндрической области для многомерного уравнения Чаплыгина имеют единственные решения.
Задача дирихле, задача пуанкаре, корректность, разрешимость, многомерное уравнение, вырождение
Короткий адрес: https://sciup.org/14318419
IDR: 14318419
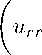
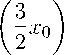
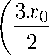
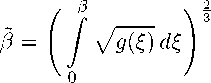
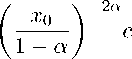
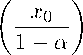
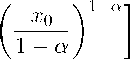
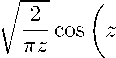
Список литературы Корректность задач Дирихле и Пуанкаре в цилиндрической области для многомерного уравнения Чаплыгина
- Hadamard J. Sur les problemes aux derivees partielles et leur signification physique//Princeton University Bulletin.-1902.-Vol. 13.-P. 49-52.
- Бицадзе А. В. Уравнения смешанного типа.-М.: Изд. АН СССР, 1959.-164 с.
- Нахушев А. М. Задачи со смещением для уравнения в частных производных.-М.: Наука, 2006.-287 с.
- Bourgin D. G., Duffin R. The Dirichlet problem the vibrating string eguation//Bull. Amer. Math. Soc.-1939.-Vol. 45.-P. 851-858.
- Fox D. W., Pucci C. The Dirichlet problem the wave eguation//Ann. Math. Pura Appl.-1958.-Vol. 46.-P. 155-182.
- Нахушев А. М. Критерий единственности задачи Дирихле для уравнения смешанного типа в цилиндрической области//Диф. уравнения.-1970.-Т. 6, №1.-C. 190-191.
- Dunninger D. R., Zachmanoglou E. C. The condition for uniqueness of the Diriclet problem for hyperbolic equations in cilindrical domains//J. Math. Mech.-1969.-Vol. 18, № 8.
- Aldashev S. A. The well-posedness of the Dirichlet problem in the cylindric domain for the multidimensional wave equation//Math. Problems Engineering.-2010.-Article ID 653215.-7p.
- Aldashev S. A. The well-posedness of the Poincare problem in a cylindrical domain for the higher-dimensional wave equation//J. of Math. Science.-2011.-Vol. 173, № 2.-P. 150-154.
- Михлин С. Г. Многомерные сингулярные интегралы и интегральные уравнения.-М.: Физматгиз, 1962.-254 с.
- Алдашев С. А. Краевые задачи для многомерных гиперболических и смешанных уравнений.-Алматы: Гылым, 1994.-170 с.
- Алдашев С. А. Вырождающиеся многомерные гиперболические уравнения.-Орал: ЗКАТУ, 2007.-139 с.
- Терсенов С. А. Введение в теорию уравнений, вырождающихся на границе.-Новосибирск: НГУ, 1973.-139 c.
- Нахушев А. М. Уравнения математической биологии.-М.: Высшая школа, 1985.-301 с.
- Алдашев С. А. Спектральные задачи Дарбу -Проттера для одного класса многомерных гиперболических уравнений//Украинский мат. журн.-2003.-Т. 55, № 1.-C. 100-107.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям.-М.: Наука, 1965.-703 с.
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 2.-М.: Наука, 1974.-295 с.
- Смирнов В. И. Курс высшей математики. Т. 4, ч. 1.-М.: Наука, 1974.-334 с.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики.-М.: Наука, 1966.-724 с.
- Алдашев С. А. Задача Дирихле в цилиндрической области для многомерного уравнения Геллерстедта//Материалы II Междунар. Российско-Казахского симпозиума "Уравнения смешанного типа и родственные проблемы анализа и информатики".-Нальчик: НИИ ПМ и КБНЦ РАН, 2011.-C. 21-22.
Статья научная
