Корректный электродинамический анализ киральных элементов и метаматериалов на основе интегральных представлений электромагнитного поля

Метаматериал – материал, природные свойства, которого обусловлены не столько природными физическими свойствами, сколько периодической микроструктурой, создаваемой человеком [1]. Метаматериалы синтезируются внедрением в исходный природный материал различных периодических элементов с самыми различными формами, которые модифицируют диэлектрическую и магнитную восприимчивость исходного материала. В очень грубом приближении такие включения можно рассматривать как искусственные, чрезвычайно больших размеров, атомы. Метаматериалы могут обладать свойствами, принципиально отсутствующими у естественных материалов, встречающихся в природе [1]. Одно из таких возможных свойств метаматериалов – отрицательный (или левосторонний) коэффициент преломления, который проявляется при одновременной отрицательности диэлектрической и магнитной проницаемо-стей [2].

Теория киральных структур в настоящее время достаточно активно развивается, но практически все новые свойства метаматериала теоретически предсказаны с помощью эффективных диэлектрической и магнитной проницаемо-стей [3]. Как правило, исследование киральных сред осуществляется с помощью феноменологи- ческой теории, материальные уравнения которой имеют вид [4]:

D = б Е + i x H , B = ц Н ± i x E .

В данных выражениях верхние знаки соответствуют киральной среде на основе спиралей с правой закруткой, а нижние знаки – среде на основе левовинтовых спиралей. Константа χ называется параметром киральности. Достоинством исследования киральных структур с помощью феноменологических уравнений является относительная простота аналитических выводов. Но здесь следует отметить усредненный характер уравнений, необходимость знания параметра киральности и его частотной зависимости для конкретной среды, малость размеров киральных элементов в сравнении с длиной волны и большое расстояние между элементами, позволяющее пренебречь их взаимодействием.

В [5] утверждается, что изучение новых свойств метаматериала с помощью эффективных диэлектрической и магнитной проницаемо-стей надо проводить очень осторожно. Ýто необходимо делать на основании строгих электродинамических методов, работающих в ближней зоне дифракции электромагнитного поля. Поэтому утверждения об одновременной отрицательности диэлектрической и магнитной проницае-мостей как об одном из свойств метаматериала требует существенных дополнительных разъяснений.

Большую часть ограничений феноменологической теории можно снять с помощью применения более строгих методов электродинамического анализа. Корректное описание элементов, соизмеримых с длиной волны, возможно только на основе строгого электродинамического подхода. К достоинствам строгого электродинамического подхода можно отнести отсутствие необходимости введения параметра киральности, снятие ограничения на размер элементов и расстояния между ними а также корректное описание ближней зоны киральных элементов.

Основным недостатком строгого подхода можно считать сложность численных расчетов и аналитических выводов. Наиболее рациональным с нашей точки зрения является комбинированный подход к анализу метаструктур, когда строгие методы анализа дополняют феноменологическую теорию, а в некоторых случаях выступают в качестве основных методов. Таким образом, построение строгих математических моделей киральных элементов и метаматериалов на их основе является актуальной задачей.

1. Основные расчетные выражения

Интегральное представление (ИП) связывает электромагнитное поле (ÝМП) в любой точке пространства с токами, находящимися в заданном объеме. Таким образом, ИП ÝМП полностью описывают излучающую структуру и окружающее ее пространство с точки зрения электродинамики.

При переходе к излучающей поверхности и применении граничных условий на ней ИП ÝМП переходят в (сингулярные) интегральные уравнения (С)ИУ, записанные относительно неизвестных распределений токов.

ИП ÝМП может иметь различные формы. Приведем здесь интегро-дифференци- альную форму [6]:

E ( r ) = Wt ivt j ( q ) k 2 G ( r , r ') )

- ( V q ■ j (q )) d B ( r , r ') dV ;                                (1)

H ( r )    J ( d x j ( q )) B ( r , r ') dV.

Данное представление не содержит дифференциальных операторов, применяющихся к точке наблюдения. В последних выражениях: r и r' – соответственно радиус векторы точек наблюдения и источника; V – излучающий объем; k – волновое число среды; Wm – вол- новое сопротивление среды; j – вектор объемной плотности электрического тока; Vq — оператор набла, применяемый к источникам поля; d = r - r' — разностный вектор; G, B — ядра интегральных представлений, которые имеют вид:

G = exp^ - iR , B = — ikR + l g

4 n R               R ¹²

R = | r - r ' | = | d | — расстояние между точкой источника и точкой наблюдения. Функцию G ( r , r ') называют также функцией Грина свободного пространства .

Ýлектродинамические модели киральных элементов и структур целесообразно строить на основе тонкопроволочного приближения [7]. ИП ÝМП тонкопроволочных структур можно легко получить из приведенных ранее интегральнодифференциальных представлений. Оно имеет следующий вид:

F ( r ) = f I ( l ') K F ( r , r ( l )) dl ', F = E , H ;               (3)

L здесь:

K E ( r , r ( l )) = W m l l o ( l^ k ² G a ( r , r ( l ')) + ik I

a

⁺ ^r(( r - r ( l )) B a ( r , r ( l )) ) l ;

d l                         )

K H ( r , r ( l )) = ( ( r - r (l )) x l o ( l ‘ ) ) B a ( r , r ( l ‘ ))

– ядра интегральных представлений;

F a ( r , r (V )) = F ( R a ( r , r ( V ))), F = G , B

– компоненты ядер; L – образующая ТПС; l – натуральный параметр на образующей;

^R a = V| ^{r - r} ' | 2 ⁺ a a

– регуляризированное расстояние между точкой наблюдения и точкой на образующей; a – радиус ТПС.

Полное ÝМП структуры, состоящей из N тонкопроволочных элементов, с учетом (3) может быть записано в следующем виде:

F(r) = 2 F(r; rj, Ij); F = E, H; j = 1, _ N; (4) j rj(l) = xoXj(l) + yoYj(l) + zoZj(l), l e [lj; lej ].

ИУ для определения неизвестных токов I _j :

• - l o ( r , ) ■ E ⁽ in ) ( r ) = l o ( r i ) ■ У Е ( г , ; r j , I j );

j                            (5)

• i ,    j = 1, ^ , N .

Здесь использовано граничное условие:

l o ( r ( l )) ■ ( e⁽ in ) ( r ( l )) + E ( r ( l )) ) = 0                        (6)

на каждом элементе структуры.

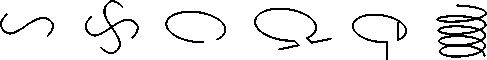
Рис. 1. ×астицы, использующиеся для построения метаматериалов

Осуществляя линеаризацию малых участков образующей, имеем:

N N j

Д

F ( r ) = EE Fa j ( r ; r j , kj , I j , kj ),   F ⁵ E, H     (7)

j =1 kj =1 ^j

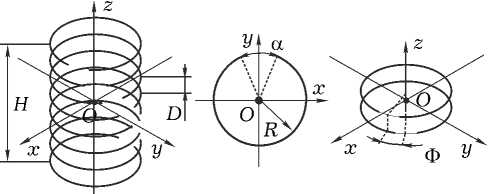
Рис. 2. Геометрически киральная структура

Интегральное уравнение (ИУ) для определения

бого сегмента [7]. Соответствующие исследования и расчеты были также приведены в [9].

неизвестных токов получаем на основе метода сшивания в дискретных точках [8] с учетом учетом граничного условия (6):

• - l o ( r- k. ) ■ E ⁽ in ) ( r * k. ) =

, _i , _i

N N j  _д

• = l 0^{( r} i , ki ) 'EE ^E aj ( r i , ki ’ ^r j , kj ’ I j , kj )             ⁽⁸⁾

• j =1 k_j =1 ^j

i = 1, _ , N, k i =1, „., N i .

Здесь r _i * _{, k} – радиус-вектор, проведенный в центр k _i -го сегмента i -го элемента.

Данное выражение целесообразно записать в виде СЛАУ:

ZI = E .                                            (9)

Ýлементы СЛАУ

Z =

I =

Корректное и устойчивое решение СЛАУ достигается при выполнении условия Д >  4 а для лю-

7\ z11

z 21

z 12

z 22

имеют вид:

2 А z 1N z 2 N

,

I ^z N 1

( 1 1 1

1 z _{N 2}

- ^z NN у

( e 1 1

i ₂

E =

e ₂

;

11N J

I e N )

2 _ z ij =

Z 11	Z 12	- Z1 Nj 1
Z 21	Z 22	•■ Z 2 Nj
Z Ni 1	Z Ni 2	•• ZNiNj y

,

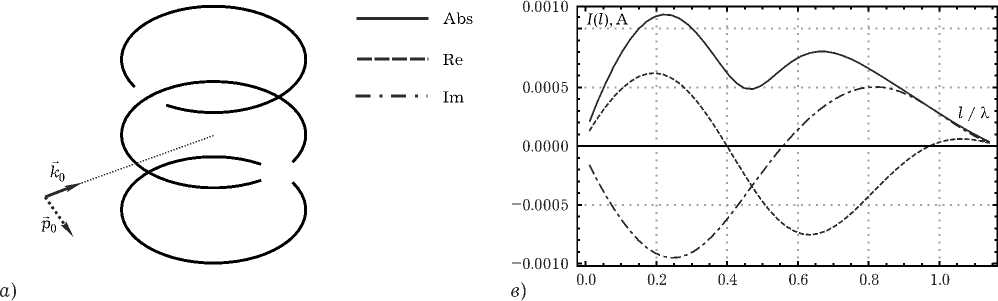
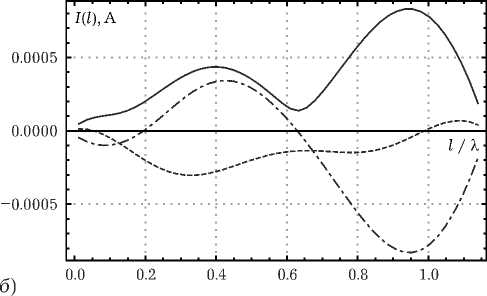
Рис. 3. Геометрия модели ( a ) и распределения токов на первом ( á ), втором ( â ) и третьем ( ã ) кольцах

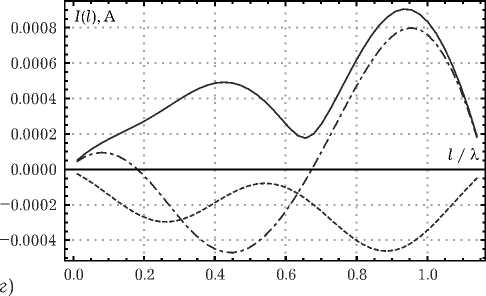
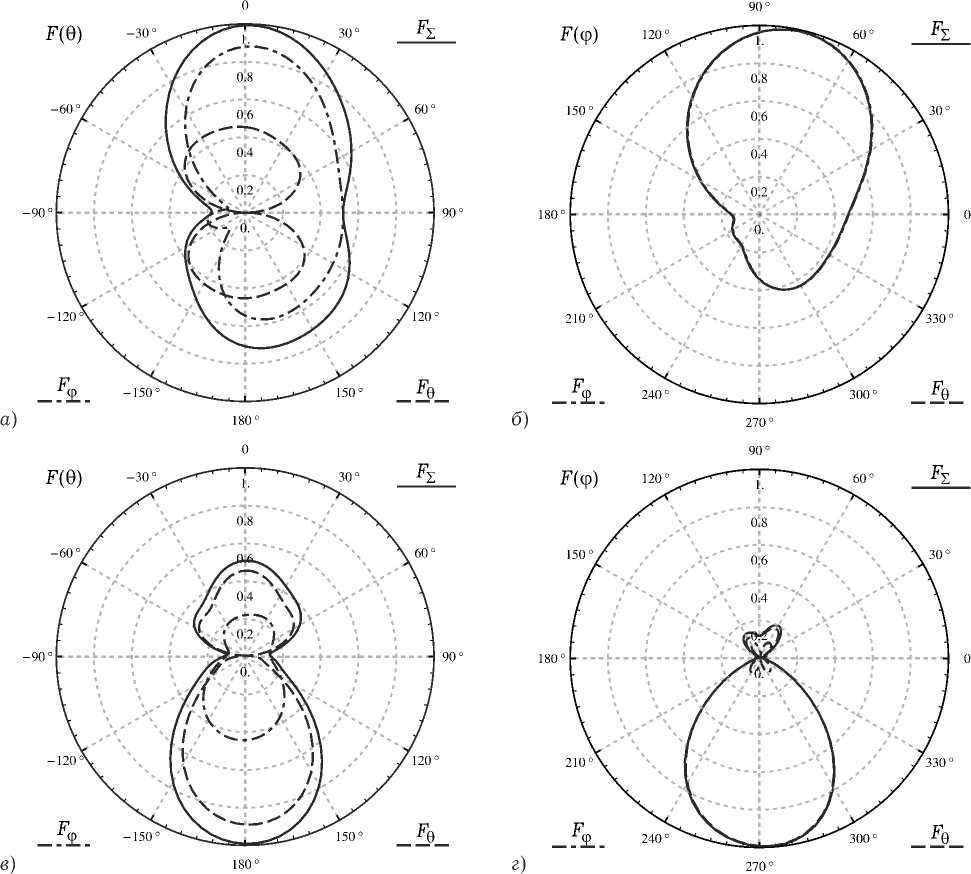
Рис. 4. Нормированные диаграммы рассеяния для ранее рассчитанных распределений тока: à ) меридианная плоскость;

б ) азимутальная плоскость; в ) R / X = 0.2; г ) R / X = 0.3; P q = У о , k o = z q , R / D = 1, a = п / 24, ф = п , N s = 50

I 1

I 2

In.

k j 7

( E 1 ) E 2

En.

k j 7

z ij = W m Ш, ki ) ■ Mr, kj ) k 2

k

^A j /2

A

^—A j /2

*                               *

G a ^{( r} i , k. , r j , k. ⁽ l )) dl + B a ^{( r} i , k. , r j , k J ;

’ i j ’ j                            ’ i j ’ j

**

B a ^{( r} i , ki , r j , kj ) = ( r i , ki

—

*

r _jk ( l )) B _a ( r _ik , r _jk ( l )) j , _j a , _ij , _j

^A j/2

^—A j /2

;

e i = l o ( r- k. ) ■ E ⁽ in ) ( r i * k. );     i , j = 1, ^ , N ,

,i,i ki = 1, —, Ni,    kj = 1, • • •, Nj •

Далее рассмотрим некоторые излучающие (переизлучающие) структуры, рассчитанные на основе выражений, приведенных в данном разделе.

2. Дифракция на геометрически киральном элементе

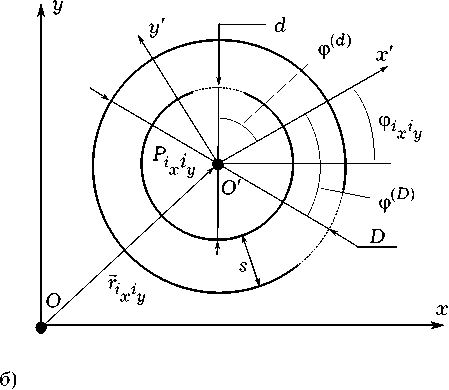
Геометрически киральный элемент (ГКÝ), показанный на рис. 2, состоит из N разомкнутых колец L : L i , L 2 , • L n • Уравнение i -го кольца имеет вид:

L i : r i ( l ) = x q R cos( l /(2 п ) + ^ i ) +

+ у о R sin( l /(2 п ) + ^ i ) + z q h i ,                    (10)

l e [—п + a; п — a], i = 1, — N,

Целесообразно положить ^ i = Ф ( i — 1); h i = D ( i — — 1) — H /2. Предполагается, что радиус проводов, образующих кольца, равен a .

В [6] представлено решение задачи дифракции на ГКÝ в случае возбуждения плоской линейно поляризованной электромагнитной волной (ПÝМВ):

E in ( r ) = P o E o exp( - i kr + V ) (11) при следующих параметрах моделирования: N = 3, а = п /6, ф = _л , N s = 50, R / D = 1, R / X = 0.2, P 0 = У o^{, k} 0 = ^x 0 , V = ⁰

Данная модель представляет собой обобщение задачи [10], где рассмотрена система из двух

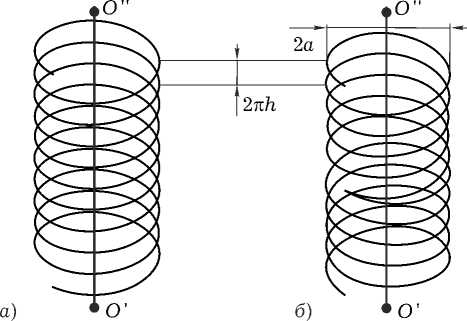
Рис. 5. Спиральные элементы разомкнутых колец. Результаты решения внутренней электродинамической задачи показаны на рис. 3, результаты для внешней задачи – на рис. 4. Из последнего рисунка видно, что в случае бокового падения электромагнитной волны при определенных геометрических параметрах структуры возникает осевое рассеяние (à), а в случае осевого падения электромагнитной волны возможно отсутствие обратного рассеяния (ã).

• 3.    Дифракция на спиральных элементах

В данном разделе представлены результаты решения задачи дифракции на спиральных элементах двух типов [11]. Первый элемент представляет собой правовинтовую цилиндрическую спираль, образующая которой описывается уравнением:

r (l ) = a cos( ^ l ) x o + a sin( ^ l ) y ₀ + + h ^ l z ₀ ,    l e [ - L /2; L /2].

Второй элемент создан на основе совмещения лево- и правовинтовой цилиндрических спиралей. Уравнения образующих:

Щ),А ----- Abs------Re------Im

• 6)    180" 2) 180"

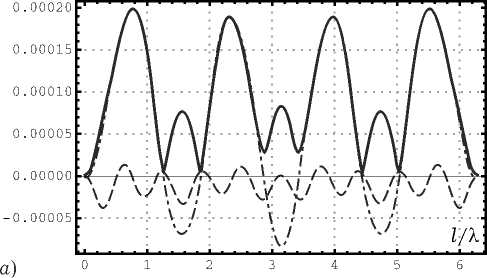
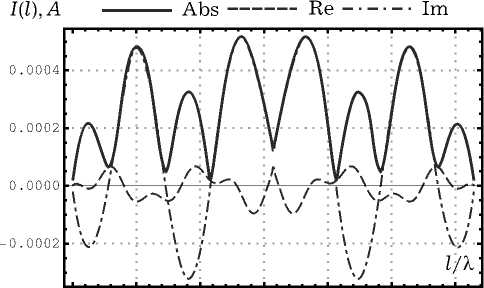
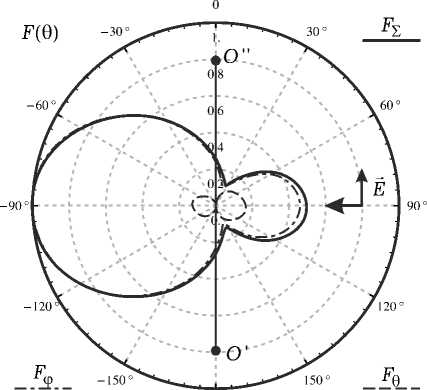
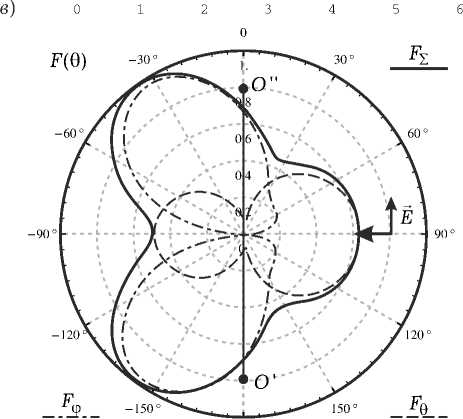
Рис. 6. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.1 Х : а ) распределение тока на спирали; б ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; в ) распределение тока на совмещенной спирали; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

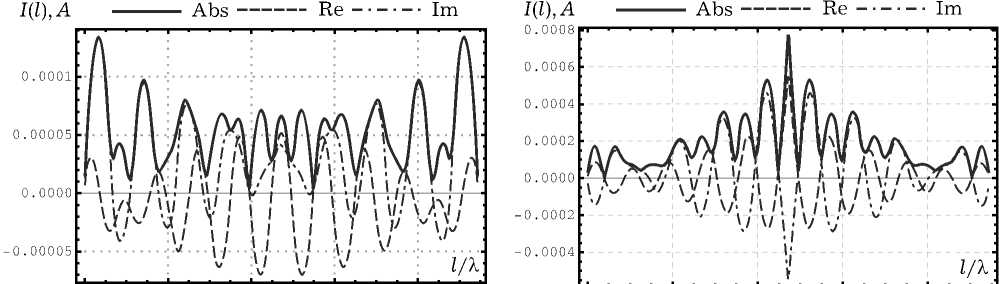
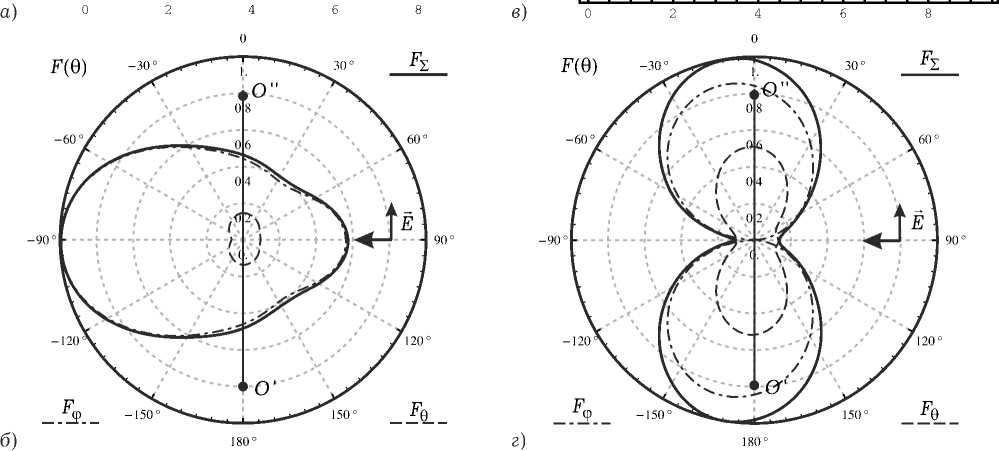
Рис. 7. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.15 X : а ) распределение тока на спирали; б ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; в ) распределение тока на совмещенной спирали; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

r 1(2) ( l ) = a cos( ^ l ) x o + a ⁸Н £ ¹ ) У о ± h ^ ^{1 z} 0 > l e [0; L /2].

В приведенных выражениях: £ = 1/ a a ² + h ²;

L – длина провода спирали; h – коэффициент намотки.

Возбуждение структур осуществлялось с помощью ПЭМВ (11), где E o = 1 В/м, у = 0, при следующих геометрических параметрах:

• •    отношение коэффициента намотки к радиусу спирали h / a = 2 / 30;

• •    радиус провода б / h = 1/10;

• •    число витков N = 10 (5 + 5 для совмещенной спирали);

• •    число сегментов N s = 500 (250 + 250 для совмещенной спирали).

• 4.    Расчет взаимодействия элементов метаструктуры

0.00020

Исследования проводились для различных соотношений a / X . На рис. 6—8 приведены сравнительные результаты.

Из рисунков видно, что несмотря на схожую геометрию элементов, решения дифракционных задач для них кардинально отличаются. Так, в отличие от обычной цилиндрической спирали со- вмещенная спираль рассеивает ПÝМВ в направлении, перпендикулярном направлению ее распространения, причем осевое рассеяние на совмещенной спирали наблюдается в широкой полосе частот, а обычная цилиндрическая спираль данным свойством не обладает. Ýффект осевого рассеяния может послужить основой для создания малоотражающих покрытий и концентраторов СВ×-энергии;

Можно утверждать, что модель совмещенной спирали в режиме осевого рассеяния является хорошим приближением для расчета совмещения слоев с разным знаком параметра кираль-ности, т. к. взаимодействие между спиральными элементами будет незначительным.

Корректное описание близко расположенных элементов, соизмеримых с длиной волны, возможно только на основе строгого электродинамического подхода, который избавляет от необходимости введения параметра киральности,

ЦГ),А ----- Abs------Re------Im Щ),А ----- Abs------Re------Im

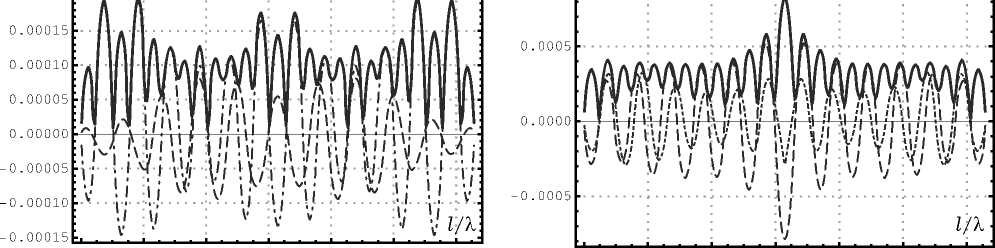
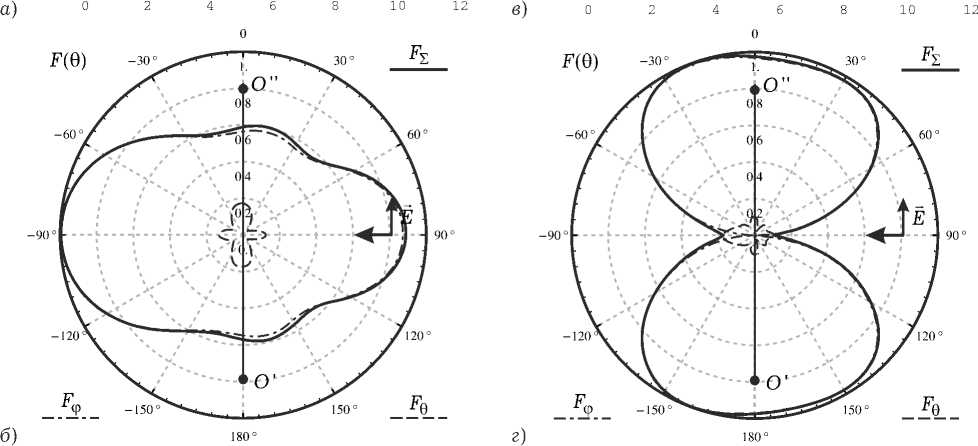
Рис. 8. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.2 Х : а ) распределение тока на спирали; б ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; в ) распределение тока на совмещенной спирали; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

снимает ограничения на размер элементов и расстояния между ними, а также дает корректное описание ближней зоны киральных элементов.

Остановимся на взаимодействии элементов. Сложность расчета в отсутствии взаимодействия составляет O ( N ), где N – число элементов структуры. Сложность расчета в присутствии взаимодействия равна O ( N ²), т. е. возрастает квадратично в зависимости от числа элементов. Таким образом, расчет структур со значительным числом элементов представляет собой проблему даже для современных ÝВМ и требует огромных затрат оперативной памяти.

С другой стороны, взаимодействие присутствует всегда, и при решении вопроса о пренебрежении им прежде всего важна количественная оценка. По этой причине актуальной задачей является построение метода расчета взаимодействия с возможностью его количественной оценки.

В [12] в качестве основы для расчета взаимодействия используется тонкопроволочное ИП

ÝМП в сочетании с модификацией метода Гаусса – Зейделя [13], оперирующего с матрицами собственных и взаимных импедансов, образующих общую матрицу системы линейных алгебраических уравнений (СЛАУ). Метод применяется для решения задачи дифракции на тонком слое метаматериала, состоящего из двойных разомкнутых колец (рис. 9).

Итерационная процедура строится по формуле:

iT ^{+ 1)} = У i e i - Z W ij i jk ) - Z w ij i k ^{+ 1)}, j > i            j < i                    (14)

i = 1, ..., N, где

У i = z ij ¹, ^w ij = У i z ij

– соответственно матрицы собственных адми- тансов и весовые матрицы.

Данная процедура расчета взаимодействия в общем случае имеет следующие свойства:

• Позволяет произвести оценку степени взаимодействия элементов по скорости сходимости итерационного процесса;

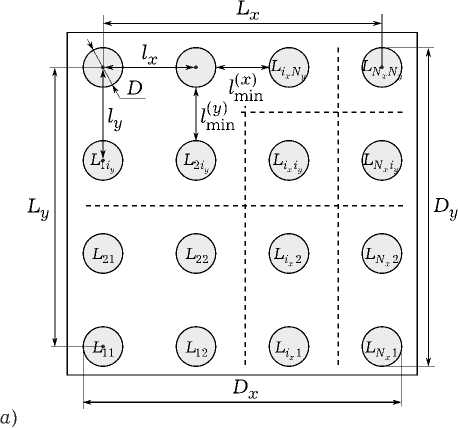
Рис. 9. Геометрия метаструктуры: à ) общий вид метаструктуры; á ) геометрия элементов

1    2    3    4    5    6    7    8    9,1          2          3          4          5

а)                                                             б)

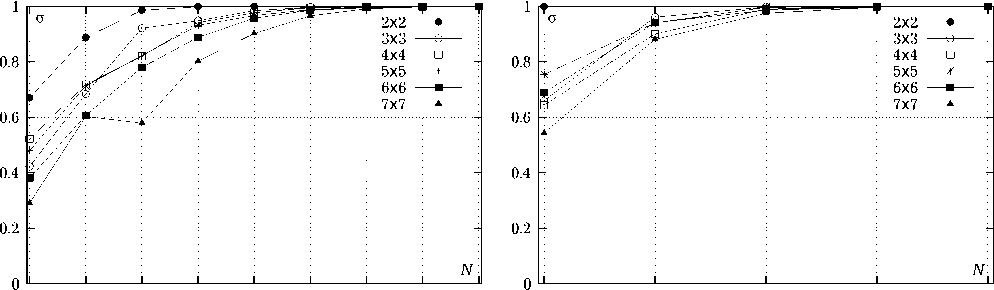
Рис. 10. Результаты оценки сходимости итерационного процесса при при увеличении числа элементов N x х N y в системе: а ) D / l = 0.8, l / X = 0.35; б ) D / l = 0.4, l / X = 0.3

• •    Позволяет оперировать матрицами взаимных и собственных импедансов а не общей матрицей системы;

• •    Обращения требуют только матрицы собственных импедансов, имеющие, как правило, небольшой размер.

В частных случаях у метода появляются дополнительные достоинства:

• •    Необходимость обращения только одной матрицы собственных импедансов в случае, когда среда образована одинаковыми элементами;

• •    Снижение числа существенных весовых матриц в случае бианизотропной среды. Под существенными понимаются матрицы, необходимые для построения общей матрицы СЛАУ.

Все это позволяет существенно сократить затраты машинных ресурсов и времени.

На рис. 10 приведены результаты анализа сходимости для метаструктуры с различным числом образующих ее элементов при различных соотношениях D / l , где l – расстояние между

элементами; D – размер элемента. Возбуждение структуры осуществлялось плоской ПÝМВ (11). Преполагалось, что E 0 = 1 В/м, у = 0, Р 0 = Х 0 , k = - z g (волна падает против оси Oz ). Критерий оценки сходимости результата строился в соответствии с неравенством:

б < 5 к

max j

( i ■

V 1

I i k + ¹) I V j X

( k ) где i _j

вектор значений токов на сегментах

j -го элемента структуры при k -й итерации. Ве-

личина, иллюстрирующая сходимость:

^ к = 7 ё ,

¹ + ⁵ к

- 3

Число б в расчетах полагалось равным 10 .

Рисунки иллюстрируют хорошую сходимость

итерационного процесса, причем скорость сходимости слабо зависит от числа элементов, образующих метаструктуру.

а)

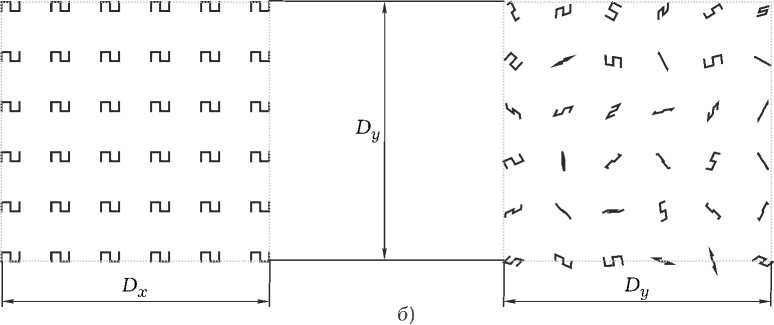
Рис. 11. Геометрия кирального слоя из S -элементов: а ) упорядоченная ориентация элементов; б ) хаотическая ориентация элементов

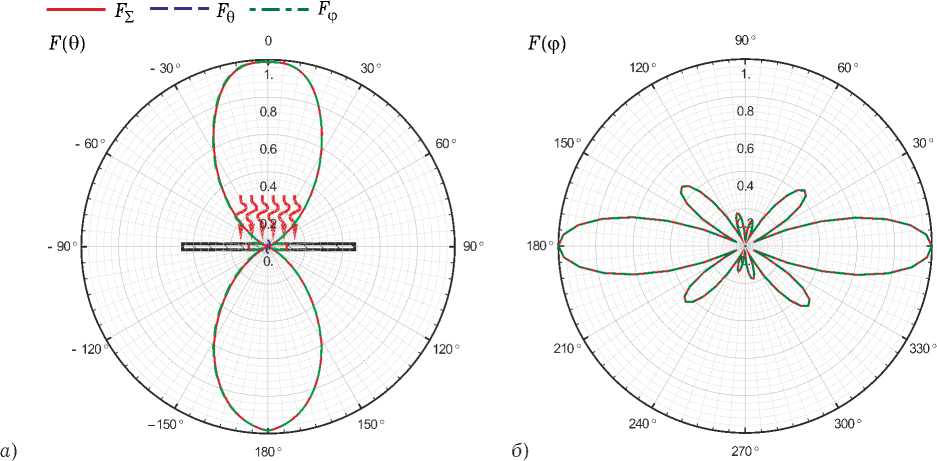
Рис. 12. Результаты расчета нормированный амплитудных диаграмм рассеяния отраженного поля от структуры, показанной на рис. 11, а : a ) меридианная плоскость; б ) азимутальная плоскость

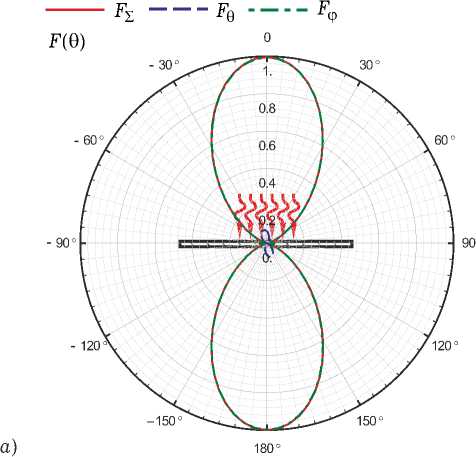
Рис. 13. Результаты расчета нормированный амплитудных диаграмм рассеяния отраженного поля от структуры, показанной на рис. 11, б : a ) меридианная плоскость; б ) азимутальная плоскость

• 5.    Дифракция ПЭМВ на киральном слое

В заключение рассмотрим результаты решения задачи дифракции на структуре, образованной S -элементами (рис. 11).

На левом рисунке они ориентированы упорядоченно, а на правом – хаотически. Структура имеет размеры D x х D y и число элементов N x х N y . На рис. 12 и 13 приведены результаты решения задачи дифракции в случае нормального падения на структуру плоской электомаг-нитной волны, линейно поляризованной вдоль оси Oy . Решение осуществлено с помощью ИП ЭМП. Параметры структуры: D x х D y = ХхХ , N x х N y = 10 х 10. Видно, что несмотря на довольно малое количество хаотически ориентированных S -элементов диаграммы рассеяния имеют вполне детерминированный характер.

Заключение

Изложены основные принципы корректного расчета киральных элементов и метаструктур на основе интегральных представлений электромагнитного поля, отражающих связь ÝМП в любой точке пространства с токами в некотором объеме либо на поверхности излучающей структуры.

Показано, что подавляющее большинство исследуемых сегодня метаструктур можно проанализировать с помощью тонкопроволочного ИП ÝМП. Подобный подход позволяет преодолеть ряд ограничений, накладываемых феноменологической теорией, таких как ограничение на размер элементов в сравнении с длиной волны и ограничение на расстояние между элементами.

Представлен эффективный метод оценки и учета межэлементного взаимодействия. На основании результатов численных расчетов, представленных в третьем разделе, можно сделать вывод о том, что переизлучающие элементы с очень близкой геометрической структурой, такие как спираль и совмещенная спираль, могут иметь кардинально отличающиеся диаграммы рассеяния.

Результаты решения задачи дифракции на киральном слое показывают, что даже при относительно небольшом числе хаотически ориентированных элементов в слое (10 х 10) диаграмма рассеяния имеет вполне детерминированный характер.

В целом хочется отметить, что приведенные ИП ÝМП, в перспективе можно использовать для решения таких важных задач, как установление четких границ феноменологической теории, определение параметра киральности (в том числе в тензорном виде), а также определение минимально необходимого числа элементов, при котором структура конечных размеров начинает вести себя как бесконечно протяженная метасреда.