Корреляционный анализ параметров вибрации для прогнозирования отказов насосного агрегата

Сегодня актуальной остается проблема обеспечения надежной и эффективной работы центробежных насосных агрегатов (ЦНА), которые используются в системе поддержания пластового давления (ППТ) и предназначены для повышения нефтеотдачи истощенных пластов нефтяных месторождений- интенсификации процесса добычи нефти [1, 2]. Выходом из данной ситуации является внедрение системы проведение ремонта агрегата по необходимости, требующей знание его фактического технического состояния в любой момент времени, который может быть определен методами технической диагностики При этом, среди всех существующих методов технической диагностики [3, 4], наиболее перспективны вибро-акустические методы, дающие возможность, на основе данных об уровне вибрации в контрольных точках агрегата, оценивать его техническое состояние и проводить диагностику неисправностей. К сожалению, сегодня отсутствуют не только общепринятые методы диагностирования ЦHА в процессе эксплуатации, но и штатные вибродатчики, не позволяющие оценить вибрационное состояние конкретного агрегата. Поэтому актуальными остаются задачи разработки методики и средств контроля их состояния за показателями уровня вибраций, в частности, по параметрам частотного спектра [5, 6].

Анализ литературы по данной теме с целью поиска примеров или эталонов спектральных распределений вибросигналов из контрольных точек центробежных насосных агрегатов при развитии у них различных дефектов значительных результатов не дал. Таким образом, при разработке методики контроля состояния ЦНА с учетом последних требований и возможностей современной измерительной техники, ставится задача установление зависимостей между видами и степенями развития вышеописанных дефектов и изменением составляющих в частотном спектре вибросигналов ЦНА, решения которой позволит определить диагностические признаки и на них основе сформировать основные положения методики.

В статье на основе обобщения, систематизации и анализа научной литературы по проблематике прогнозирования неисправностей насосного агрегата, анализируются математические модели вибрационных сигналов, их неправильная обработка и интерпретация системой, включается прогноз неблагоприятных событий, таких как помехи, всплески и т.п. и их поведение [2].

Согласно промышленным данным, наиболее распространенными типами отказов насосного оборудования системы поддержание пластового давления представляет собой выход из строя подшипников, рабочих колес и направляющих аппаратов, зубчатой соединительной муфты.

Среди дефектов, предопределяющих эти отказы можно выделить следующие основные: разбаланс, расцентровка валов насоса и приводного двигателя (радиальная и торцевая), искривление вала, износ и деформации поверхностей лопастей рабочих колес, дефекты подшипников качения и скольжения, ослабление механической крепи насоса к фундаменту.

В рамках выполнения практической части задачи корреляционного анализа параметров вибрации для прогнозирования отказов насосного агрегата составляется обобщенный анализ математической авторегрессионной модели (АР) прогноза сигналов, которые система обрабатывает с ошибкой или с присутствием помехи, подключаются, в том числе и статистические данные в качестве практического массива информации для прогноза. Сама модель прогнозирования неблагоприятных событий, идущих в сигналах, разделяется на три последовательных этапа [7-12]:

• 1)    создается порядок работы авторегрессионной модели прогноза;

• 2)    составляется оценка полученных данных АР модели;

• 3)    на основе обзора оценки получаем вероятностный прогноз отказного элемента.

Опишем первый этап - создание порядка работы авторегрессионной модели прогноза. На данном этапе определяется p -количество измеряемых параметров модели. За счет функций вида частной автокорреляционной и корреляционной задается описание временного ряда авторегрессионной модели. При этом в процессе прохождения p - порядка авторегрессии частная автокорреляция покажет как обрыв p – помеха, а автокорреляция снизится постепенно. Определяем порядок работы АР модели и вычисляем:

• 1)    дисперсию о² сигнала и среднее выражение z ряда работы элементов:

о2 = 1 Z=i(zi — Z)2; z = 1 Z^z ,

здесь n - общее количество элементов ряда; Z i - роль временного интервала рядов на период времени i, i = 1,n.

• 2)    ряд с автоковариационной функцией O r ^:

Где C_o = о²;

C r = - Z F=1 ^R(Z j - Z)( z_{i +} n - Z i ), R = 1,K.

• 3)    ряд с автокорреляционной функцией ^rR ^:

r R =   , R = oTK         (2)

^o здесь K - максимальный простой авто-ковариационной и автокорреляционной функций;

• 4)    функцию частотной автокорреляции:

  
  
  

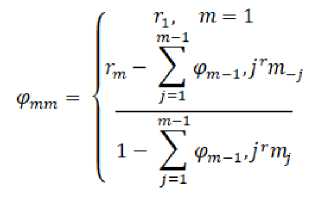
m = 2,K ,      (3)

^здесь (p _mj =

_m-i'j- <р_тт^_т__11т_. J = 1, m ^-1; M - максимальый простой частотной функции автокорреляции.

Немного иным способом выбираются K, L. В результате опытных исследований, K, L выбираются состояния сигнала 20

Второй этап, составление оценки полученных данных АР модели.

АР модель составляется по методу зиционируется как линейная модель с ми-наименьших квадратов, поскольку она по- нимальной дисперсией:

°а = ;^ ^t=_P+i^а = ^--1 TJ=_p+i^(zt^-SJ=1 bj ^-j) ^ min.

Такой путь приводит нас к получению системы нормальных уравнений.

Ж=_Р=1 ^zt- j ^(zt^-Xj-i bj ^z_t-j) = о, j = 1, P.

Эти уравнения необходимо решать сравнительно Ъ1, b₂, , b_p, для, получения характеристик событий сигналов (вы-брационных импульсов) на каждом шаге модели автокорреляции.

Выясним состояние произвольной величины дисперсии a_t: а а = St=₁а^/(n - p) и неизменяемую составляющую: 0_О= z (1 — Sf=i bi). В зависимости от величины полученных данных проходит пробитие сигнала или он протекает в допустимом спектре.

Третий этап, на основе обзора оценки математических данных модели удастся получить вероятностный прогноз предвестника отказного элемента.

Главной стратегией используемой в модели это создать такое условие, при кото- ром прогнозируемый средний результат будет незначительно отличаться от истинного положения показателей в работе на опережение отказа I. Чем точнее будет прогноз, тем успешнее могут быть действия по оценке риска катастрофы. На точность в прогнозе влияет и допустимый временной интервал, заданный на его выполнение. Внутри намеченного интервала, вероятность точности прогноза отказного элемента по изучению его импульса, будет, например, 65-95% но может меняться в зависимости от длительности интервала.

Также стоит рассмотреть, что минимальная среднеквадратичная ошибка в прогнозировании может вычисляться согласно заданной формуле:

z_t(l) = 00 + Zf₌iJ( [z,-i_+l];

zt-i+l

(zt(i-i), ь >t; Izt-i+i,L ^i, в примере zt (l) - столько шагов прогноза наперед на временной отрезок t; zt-i+i - показатель временного отрезка на период времени t — i + I; 1 = 1, L, где L -прогнозирование (контролирование ложных срабатываний) на максимально возможное опережение.

Из примера показанного выше (5) можно сделать вывод, что формула прогноза достаточно рекуррентна и предоставляет возможность, в связи с появлением нового количества информации выполнять прогнозирование свободно проводить корректирующие действия, что, несомненно, дает ощутимое преимущество в процедуре прогнозирования.

Есть и другой вариант выйти на точный прогноз по этой модели следующим способом. Верхние и нижние границы отыскиваются, вычисляя z_t+i = z_t (I) ± UJV (I), имеем U = 0, 70; 1,66; 1,97 или 2,60 в данном варианте все будет зависеть от пределов интервала с вероятностью 0,50; 0,90; 0,95 либо 0,99, в конечном счете, гипотеза предполагает нахождение допустимого предела отклонения.

Выражение дисперсии будет равно:

V(I) = rf ij^o tf, здесь,

(     1,J = 0;

^   \y^J (0- ■ ■   / > 1

^L==^upj-i, J — 1

j = 1, L; bi = 0, i > p.

Построение прогноза с использованием авторегрессионной математической модели позволяет получить высокую степень точности результатов в определении ложных срабатываний сигналов.

По результатам анализа параметров вибрации для прогнозирования отказов насосного агрегата в данной статье, очевидно, что математическая авторегресси- онная модель показывает высокие результаты в прогнозе на упреждение, помогает отследить предвестник и сделать прогноз отказа, а также выработать меры по пре- дупреждению этого отказа. Но это существенно будет зависеть и от предыдущих условий, в которых система наработала. Вероятность прогноза может доходить до 95,% и подтверждена моделированием или лабораторными испытаниями. Также существуют более сложные математические модели и методы с использованием различных нелинейных параметров, автокор- реляции, сложных процедур, которые обеспечивают и более точные результаты прогноза.