Космологические антиномии И. Канта в критическом изложении П. А. Флоренского

Введение.

Когда заходит разговор о влиянии идей И. Канта на русскую религиозно-ориентированную философию, то следует согласиться с Н. В. Мотрошиловой, что « кантовская философия – как никакая другая (за исключением учений Платона, Шеллинга и Гегеля) – предоставила мыслителям России весьма ценный стимул для самостоятельного философствования, ибо были восприняты и подвергнуты критике центральные идеи и принципы Канта (курсив Н. В. Мотрошиловой. – Авт. )» [2: 199]. Среди этих идей особое внимание уделялось русскими философами идеалистического направления Серебряного века учению Канта об антиномиях чистого разума. Антиномизм как теоретико-методологический принцип был основой философских концепций Е. Н. Трубецкого, П. А. Флоренского, С. Н. Булгакова, С. Л. Франка. Одним из основоположников принципа антиномизма в русской философии был П. А. Флоренский. С. Б.

Основной текст.

Флоренский уделяет особое внимание идее мира Канта и антиномиям как следствиям из нее. Каждая антиномия представляют собой случай, когда берутся два взаимоисключающих суждения, тезис и антитезис, при этом истинность каждого из них может быть доказана. Так, можно логически обосновать конечность и бесконечность мира при определении его количественных характеристик. Определяя качественные характеристики мира, можно одинаково доказать, и что мир можно делить до бесконечности, и что нельзя. Исследуя вопрос о наличии причины в мире, можно утверждать, что существует первопричина, а также можно утверждать, что ее нет. Можно доказать, что в мире или вне его действует Бог, можно доказать обратное [8: 603]. Такой ход рассуждений Кант называет антитетикой [3: 337].

Затем русский философ разбирает кантовские доказательства антиномий. Первая антиномия представляет собой рассуждения о величине мира. «Мир имеет начало во времени и ограничен также в пространстве» [3: 341] – это тезис. «Мир не имеет начала во времени и границ в пространстве; он бесконечен и во времени, и в пространстве» [3: 342] – гласит антитезис. Флоренский утверждает, что Кант в этом случае обращается к доказательству от противного. У мира есть начало во времени. В противном случае тогда бы до начала мира протекала бы вечность и прошел бы бесконечный временной ряд. Однако прошедший бесконечный ряд не может быть закончен присоединением конечных частей, иначе бы момент настоящего не настал, из этого следует, что этот ряд невозможен, и значит, что у времени есть начало. После этого доказывается ограниченность мира в пространстве. Кант утверждает, что бесконечное протяжение не может быть помыслено в конечном времени [8: 603]. С целью доказательства антитезиса выдвигается гипотеза о бесконечности мира в пространстве и во времени. Тогда следует предположить существование вне мирового времени и мирового пространства, незаполненного миром времени и пространства, которые находятся в отношении к началу и к границе мира. Но это абсурд. Поскольку ни один момент времени не является каким-то особенным, чтобы считать его началом мира. Точно также какая-то часть пространства, принадлежащая миру, ничем не отличается от другой части мирового пространства. Следовательно, мир бесконечен во времени и в пространстве [8: 604].

Вторая антиномия повествует о содержании мира. Тезис: «Всякая сложная субстанция в мире состоит из простых частей, и вообще существует только простое или то, что сложено из простого» [3: 347]. Антитезис: «Ни одна сложная вещь в мире не состоит из простых частей, и вообще в мире нет ничего простого» [3: 348]. Чтобы доказать тезис, Кант снова использует доказательство от противного и формулирует мысль о том, что в мире нет ничего простого. Если допустить существование одного сложного, то тогда оно равно нулю, что означает отрицание бытия. «Значит, либо сложения нельзя мысленно удалить, либо должно, по его удалении, остаться нечто простое. В последнем случае тезис доказан; а в первом выходило бы, что сложное не состоит из субстанций (ибо сложность для субстанции есть лишь случайное отношение и, как таковое, может быть абстрагировано, и, следовательно, само не есть субстанция), что противоречит условию тезиса» [8: 604]. При обосновании антитезиса тоже применяется апагогическое доказательство, предполагается, что сложное является синтезом простых элементов. Синтез элементов осуществляется в пространстве, а пространство, в котором расположена сложная вещь, состоит из пространств, занятых элементами. Следовательно, простое находится в пространстве. Однако, все, что развернуто в пространстве, представляет собой сложное, образующее многообразие из субстанциональных частей, расположенных вне друга друга. Значит, простое является сложным, но это – противоречие. Поэтому сложное не состоит из простого. Но простое не существует и вне сложных вещей. «Это видно из того, что если бы было в мире что-нибудь простое, то оно могло бы сделаться объектом опыта и, как таковое, имело бы последовательность состояний во времени и вне-положность частей в пространстве. А, следовательно, такой объект опыта не был бы простым» [8: 605].

В третьей антиномии рассматривается вопрос о порядке в мире – о конечности или бесконечности причинной цепи явлений. В тезисе говорится, что: «Причинность по законам природы есть не единственная причинность, из которой можно вывести все явления в мире. Для объяснения явлений необходимо еще допустить свободную причинность» [3: 353]. Этому тезису противостоит антитезис: «Нет никакой свободы, все совершается в мире только по законам природы» [3: 354]. С целью доказать тезис допускается существование только природной причинности. Тогда следует допустить, что начало мира тоже имеет причину, и так до бесконечности. Это означает, что постоянный поиск причины делает бессмысленным этот поиск. Чтобы избавиться от такой дурной бесконечности следует допустить ниоткуда невыводимую первопричину, порождающую цепь явлений, существование которых уже объясняется законом причинности. Такая первопричина называется трансцендентальной свободой [8: 605–606]. В случае доказательства антитезиса свобода трактуется как частный случай причинности. Но тогда бытие первой причины следует рассматривать как два разных состояния. Первопричина, несвязанная с явлениями, – это первое состояние. Второе состояние характеризуется наличием причинно-следственного ряда. Поскольку первопричина и есть свобода, то она не может быть началом явлений, так как в противном случае это бы противоречило самому понятию свободы. Следовательно, нет свободы, существует только природная причинность [8: 606].

Четвертая антиномия посвящается вопросу существования мира. В тезисе сказано: «К миру принадлежит или как часть его, или как его причина безусловно необходимая сущность» [3: 359]. В антитезисе утверждается обратное: «Нигде нет никакой абсолютно необходимой сущности – ни в мире, ни вне мира – как его причины» [3: 360]. Эта антиномия отличается от предыдущих трех. Доказательство тезиса осуществляется прямо. Признается, что чувственный мир изменчив. Любое изменение имеет причину, поэтому следует допустить существование первопричины, абсолютно-необходимого. Затем Кант допускает, что необходимое существо принадлежит чувственному миру, т. е. должно считаться началом мира. Но начало какого-либо явления должно предшествовать ему во времени. Атак как необходимое существо вне-мирное, то тогда оно должно быть и вне-временным, т. е. оно не может быть началом мира [8: 606–607]. Антитезис доказывается от противного. Предполагается, что необходимое существо находится или в мире, или вне его. Если это существо находится в мире, то оно или его часть, или целый мир. В качестве части мира оно должно быть безусловным началом мира. Однако безусловного начала быть не может по определению самого понятия «начало мира», которое дает Кант. Вместе с тем необходимое существо не может быть безначальным целым миром, так как мир бесконечно изменяется, и сумма этих бесконечных изменений не дает необходимого существа. Таким образом, необходимого существа нет в мире. Но этого существа не может быть и вне мира. «Потому что оно должно быть причиною мирового ряда, а причина начинает обусловленный ею ряд и находится, следовательно, во времени. Значит, необходимое существо должно было бы находиться не вне мира, а в мире, – невозможность чего доказана уже. Итак, его нет ни в мире, ни вне мира, т. е. – нет вообще» [8: 607]. Флоренский делает вывод, что первые две антиномии не имеют отношения к космологии, поскольку в них идет речь о мире в целом, но мир ноуменов не может рассматриваться как пространственно-временное явление. Если речь идет о мире феноменов, то тогда либо тезис, либо антитезис следует признать в качестве истинного, в таком случае говорить об антиномиях не имеет смысла. Иначе философ характеризует третью и четвертую антиномии. Он считает, что в третьем и четвертом случае и тезис, и антитезис может быть доказан в качестве истинного, если различать мир ноуменов и мир феноменов. Бесконечный причинно-следственный ряд явлений, исключающий абсолютную необходимость, относится к миру феноменов. В мире ноуменов действует абсолютное существо и свобода. Эти два мира могут сосуществовать, поскольку они разнородны [8: 609].

После краткого изложения доказательств антиномий Канта Флоренский обращается к вопросу об исторических предпосылках учения об антиномиях Канта. По его мнению, на Канта повлиял спор относительно пространства и времени И. Ньютона и В. Лейбница. Лейбниц утверждал, что пространство и время являются следствием вещей метафизических, которые и есть подлинная реальность. Ньютон считал, что существует чувственный мир, а пространство и время – это субстанции [8: 610–611]. Кратко суть спора между двумя мыслительными парадигмами Флоренский формулирует в виде математического вопроса: «Дифференциал или производная?» [8: 610]. Лейбниц трактует «дифференциалы как сверхчувственные элементы вещей» [8: 611], для Ньютона они – только «фикция, посредством которой косвенно можно связать одну величину с другой в пространстве, которые поэтому находятся в отношении – в виде производной» [8: 611]. Таким образом, «рационализм с метафизикою шли под флагом дифференциалов ; эмпиризм с феноменизмом – под флагом производных » [8: 611]. На Канта, по мнению Флоренского, повлияло пиетическое воспитание и необходимость изучать метафизику и естественные науки во время учебы в университете. «Столкновение пиетизма и естественных наук в сознании Канта породило две последние, динамические антиномии, тогда как столкновение метафизики и натурфилософии – две первые, математические» [8: 611]. Он пишет, что Кант стремился использовать положения двух вышеупомянутых концепций при построении своей системы трансцендентального идеализма, не желая подняться над этим спором мысленно и углубиться в религиозную мистику. Антиномии немецкого философа, с его точки зрения, есть компромисс, заключающийся в признании сосуществования двух противоречащих суждений без поиска взаимосвязи между ними [8: 612]. Согласно Флоренскому, в этом заключается «слабость» мысли Канта. Он отмечает, что Кант пытался рассматривать спор двух парадигм с точки зрения римского права, именно там случай, когда закон противоречит самому себе, называется антиномией. Флоренский высказывает предположение, что понятие «антиномия» для своей системы Кант позаимствовал оттуда [8: 614].

Во-вторых, Флоренский обоснованно утверждает, что Кант отождествляет протяженность и материю при построении антиномий, хотя в других работах учитывает различие между ними, «зная, что количество материи характеризуется не величиною протяжения ее, а массою » [8: 616]. Именно по этому вопросу Флоренский высказал в своей лекции ряд важных замечаний, имеющих значение для понимания антиномичности разума и, в целом, для понимания феномена мышления в современной науке и философии.

Так, ошибкой Иммануила Канта является то, что он полагал, что решение задачи о протяженности мира в пространстве включает все методы миропонимания, поскольку как в случае ограниченности мира по протяжению, то есть его конечности, так и в случае его неограниченности в пространстве, масса мира может быть как равна конечному числу, так и равна ∞, что зависит от функции плотности (материи) как координатной функции. Дадим математическое объяснение этого вопроса.

Введем следующие обозначения: M – масса мира; p (x, у, z) – функция плотности (материи) в точке (х, у, z); a1, а2, b1, b2, с1, с2 – гпределыиинтегрирования р дляккоординатXx,уy, zссоответственно.тТогд массу мира можно рассчитать по следующей формуле:

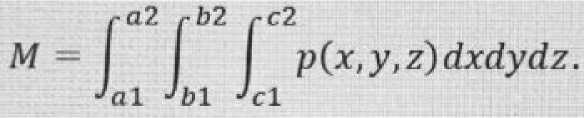
Если совместить декартову систему координат со сферической системой координат, то некоторая точка мира A с координатами (х, у, z) будет иметь координаты (r, φ, q), где r - длина радиус-вектора точки А; j является углом между осью абсцисс и проекцией радиус-вектора точки А на координатную плоскость xОy, отсчитываемый от оси абсцисс в положительном направлении; q есть угол между осью аппликат и радиус-вектором точки А, отсчитываемый от положительного направления оси аппликат. Сферические координаты варьируются в следующих пределах:

С учетом якобиана перехода от прямоугольных (декартовых) координат к сферическим имеем [4: 21 – 22]:

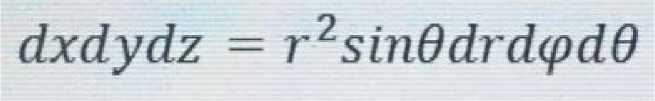
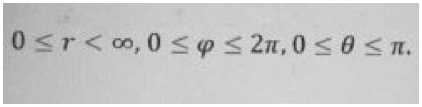
Тогда, считая, что мир не конечен, а бесконечен по протяжению, вычислим массу мира по следующей формуле:

M' - f^dyf^sinO f“ r²p(r)dr ~ (ylo^) • (-cos0|£) • ^ p{r)r²dr

/•00                          < oo

= (2л - 0) ■ (-COST! + cost)) • I p(r)r²dr - 4n I p(r)r² dr

Однако неотрицательные величины М и М' могут быть и равны ∞, и меньше ∞ при любых пределах интегрирования; их значение определяется функцией плотности р(х, у, z) или р(r) соответственно.

Для наглядности и лучшего уяснения вышеописанного вопроса о величине массы мира Флоренский использует геометрию, а именно – геометрический образ.

Суть этого образа заключается в следующем: обозначим через А некоторую точку мира, лежащую в некоторой замкнутой поверхности S, а эту поверхность охватывает тело, объем которого обозначим через V; обозначим через M массу, содержащейся в V материи. Построим вокруг А последовательность

объемов

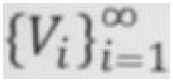
для возрастающей последовательности поверхностей

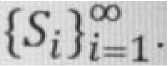
вводим предположение: либо при

E. где I

Далее

–

конечная граница мира, либо

, если мир по протяжению в пространстве является бесконечным. Тогда для

(MJSi

(возрастающая последовательность масс, которая соответствует

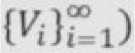
, числовой

ряд

у» 00

2.^1

Mi либо сходится и имеет пределом конечное число M (именуемое Флоренским массой

мира), либо расходится. В первой антиномии Кант утверждает, что одинаково строго можно доказать и то, что числовой ряд масс сходится, и то, что он расходится, что с математической точки зрения невозможно.

Аналогично доказательство второй антиномии Канта содержит ошибки. В данном случае Флоренский строит убывающие последовательности объемов, соответствующих убывающим поверхностям, расположенным внутри S. В данном случае Иммануил Кант утверждает, что одинаково можно доказать, что числовой ряд, состоящий из соответствующих этим объемам масс, всегда сходится и имеет пределом 0 (непрерывность материи), и иногда имеет пределом число, не равное 0 (атомистическое строение материи), что с математической точки зрения абсурдно [8: 618]. Также необходимо отметить, что этот числовой ряд масс, вообще говоря, может и расходиться, что Кант не учитывает (Флоренский заметил).

Итак, если обратиться к доказательствам четырех антиномий Канта, то, по крайней мере, в первых двух математических антиномиях есть ошибки. Флоренский в своей пробной лекции «Космологические антиномии И. Канта» сожалеет, что наиболее интересную для него часть чтения ему пришлось скомкать и сократить [8: 621]. В данной статье с помощью сотрудничества философа и математика (соавторы статьи) частично восполнено то, о чем он сожалел, а именно, было проведено исследование доказательств математических антиномий Канта. Отметим, что в данной статье рассуждения самого П. А. Флоренского [8: 618] даны с более точной с математической точки зрения корректировкой (заменой) в некоторых местах понятия «ряд» на «последовательность», «группы» (чисел) – на «числовой ряд». Флоренский ограничился рассмотрением математических антиномий Канта, сославшись на нехватку времени.

Однако, несмотря на несовершенные доказательства, Флоренский отметил в качестве главной заслуги Канта его идею об антиномичной структуре разума. «По природе своей разум имеет закал антиномический, ибо разум дву-законен, дву-центрен, дву-осен. А именно, в разуме статика его и динамика его исключают друг друга, хотя, вместе с тем, они не могут быть друг без друга» [8: 624]. Статическое мышление ориентируется на закон тождества (к которому Флоренский условно относит и закон противоречия, и закон исключенного третьего): «А есть А», так как мысль не охватывает беспредельность в целом, но изучает ее, разделив на предельные статичные элементы. Чтобы определить А, надо его отделить от ( (не-А).flДинамическоеVмышление стремитсяЭобосноватьПпоняти

(построить доказательство), поэтому ориентируется на закон достаточного основания. Чтобы объяснить А, надо вывести его из источника не-А, т. е. из Б. В работе разума русский философ обнаруживает герменевтический круг. Чтобы идти от А к Б, надо установить А как А, мыслить А ясно и отчетливо. Однако, чтобы мыслить определенно А, надо объяснять и доказывать А как не-А. Разуму нужны обе нормы, без них он не может познавать. Вместе с тем разум не может одновременно мыслить двумя несовместимыми способами. Поэтому Флоренский приходит к выводу: «Нормы разума необходимы, но они – и невозможны. Разум сказывается насквозь – антиномическим, – в своей тончайшей структуре. Кантовские антиномии – только приоткрывают дверь за кулисы разума. Но будучи выставлены с полною сознательностью и в упор эпохе просветительства, с вызовом рационализму XVIII-го века, они являются великою моральною заслугою Коперника философии» [8: 626].

Заключение.

В результате анализа статьи Флоренского «Космологические антиномии И. Канта» можно сделать следующие выводы. Флоренский очень высоко оценил учение об антиномиях разума Канта. По его мнению, Кант был первым, кто поставил этот вопрос в рамках космологии и гносеологии и попытался вывести логические следствия из такой постановки вопроса. Признавая антиномичность разума, русский мыслитель не соглашался с идеей Канта об отношении истины и разума. К. А. Сергеев писал, что, согласно Канту, истина есть достоверность. «Сколько явления, столько и самой бытийности вещей, раскрываемой человеческому разуму, и никакой иной познаваемости в человеческом опыте постижения сущего нет и не может быть вообще. Другими словами, феномены подлинного человеческого опыта заключают в себе всю полноту постигаемой достоверности» [6: 107]. По Канту, автономный субъект по своим законам устанавливает истину, хотя и не абсолютную. У Флоренского – в отличие от Канта – разум утверждается через Истину. В своей работе «Столп и утверждение истины» он пишет, что истина выражает сущее как всеединое, поэтому она больше разума. Исследуя способности разума и его антиномичную природу, Флоренский приходит к мысли о несостоятельности разума и о необходимости укоренения последнего в Абсолютной Истине. При этом вопрос о существовании Истины Флоренским постулируется как догмат [7: 731]. Если Кант настаивал на строгом разграничении науки и метафизики, то Флоренский считал, что наука имеет метафизический статус, что необходимо построить концепцию «цельного знания», чтобы связать науку с религией в едином дискурсе. В отличие от В. С. Соловьёва, предложившего концепцию «цельного знания», Флоренский считал, что наука не способна «свободно» усвоить религиозные истины, но возможно научные построения совместить с содержанием религиозных учений, что можно сделать в рамках науки математики. Именно математика создает возможности для созерцания софийного облика бытия, воплощения Божьего замысла в космосе [7: 734–735]. С точки зрения С. М. Половинкина, на формирование таких взглядов Флоренского повлияли идеи аритмологии основателя Московской философско-математической школы Н. В. Бугаева, обогащенные идеями теории множеств Георга Кантора [5: 621]. Сутью аритмологии является теория прерывных функций. Идею прерывности как нового миросозерцания XX века Бугаев противопоставляет аналитическому мышлению эпохи Нового времени. «Своей аритмологией Бугаев пытался примирить монизм с плюрализмом, коллективное с индивидуальным, материю с духом, физику с историей, причинность с целесообразностью, необходимость со свободой» [5: 623]. Флоренский вслед за Бугаевым считал, что аналитическое мышление не может объяснить свободу, веру, подвиг, творчество, красоту. Он рассматривает непрерывность как частный случай, модификацию прерывности, что наиболее ярко продемонстрировано им через идею актуальной бесконечности. Под актуальной бесконечностью «в математике понимается завершенное бесконечное множество, уже осуществившееся, в отличие от потенциальной бесконечности – множества, способного неограниченно возрастать (убывать), становясь больше (меньше) любой наперед заданной величины» [7: 738]. По Флоренскому, потенциальная бесконечность является переменной, а актуальная бесконечность – константой. С его точки зрения, потенциальная бесконечность может рассматриваться символом философии Нового времени [7: 739]. За неимением времени Флоренский не стал в статье об антиномиях Канта подробно разбирать учение об актуальной бесконечности. Однако русский философ считал, что Кант, хотя в своих ранних работах правильно понимал идею бесконечности, но когда писал «Критику чистого разума» неправильно истолковал понятие бесконечности, поскольку он отрицал бесконечность в виде константы, но рассматривал ее в виде переменной [8: 621]. Кант ориентировался на понятие потенциальной бесконечности при построении доказательств своих антиномий, поэтому он совершил ряд ошибок с точки зрения математической теории, основанной на идее актуальной бесконечности. Отсюда видно, что решающим фактором при понимании проблемы антиномий разума являлся выбор оснований для математических доказательств, определяемый мировоззренческими позициями Канта и Флоренского.

По сути вопрос об антиномиях стал полем битвы между новоевропейской философией, ориентирующейся на идею автономности разума, и русской метафизической традицией, идеалом которой была идея всеединства. Размышления Флоренского отличаются от позиции Канта еще и тем, что русский мыслитель не трактовал антиномии как непримиримые противоречия, согласно ему, тезис и антитезис представляют собой не только противоположности, но вместе с тем образуют тождество. Они как бы взаимопроникают друг в друга своими энергиями. Позднее подобный подход был развит в квантовой физике в виде принципа дополнительности Н. Бором. В современной философии учение о космологических антиномиях Флоренского как возрождение традиционной полноты мировоззрения может рассматриваться альтернативой как технократическому рационализму, так и постмодернистскому иррационализму.