Космологические модели, основанные на асимметричном скалярном дублете с кинетической связью компонент

В [1] была подробно исследована космологическая модель, основанная на асимметричном скалярном Дублете Хиггса, в котором классическая Ф и фантомная ф компоненты взаимодействуют лишь посредством гравитационного поля. Заметим, что ранее в [2–4] были получены и изучены некоторые однопараметрические классы точных решений для космологической модели, основанной на классическом и фантомном полях при специальном выборе функции потенциальной энергии. Позже в работе [5] были исследованы космологические модели, основанные на скалярном квинтоме с взаимодействием между классической и фантомной компонентами при специальном выборе функции потенциальной энергии в виде экспоненты. Далее в [6, 7] на основе теоретической модели статистической системы скалярно заряженных фермионов с Хиггсовым потенциалом взаимодействия [8] были исследованы космологические модели, в которых взаимодействие между компонентами асимметричного скалярного дублета осуществлялось посредством скалярно заряженных фермионов. В этих работах представлена богатая коллекция космологических моделей, среди которых есть модели с конечным прошлым (начальная сингулярность возникает в конечный момент времени t0 >  -∞ ) и конечным будущим (конечная сингулярность возникает в конечный момент времени t g < + ^ ). В частности, в [7] было исследовано поведение космологических моделей вблизи сингулярностей t → t _s и показано, что вблизи сингулярностей достигается суммарное ультрарелятивистское уравнение состояния материи

p

^к = Ё т 3 ,

(at t т t s ).

Далее, в [9] были изучены трансформационные свойства космологических моделей по отношению к преобразованиям подобия фундаментальных констант.

В связи с проблемами образования сверхмассивных чёрных дыр в ранней Вселенной в серии работ [10] – [11] была построена теория скалярно-гравитационной неустойчивости систем ска-лярно заряженных фермионов и предложена модель образования сверхмассивных чёрных дыр, удовлетворительно объясняющая основные характеристики этих объектов. Таким образом, модели скалярных полей с нелинейным взаимодействием могут играть важную роль в космологии и астрофизике ранней Вселенной. В рассмотренной выше серии работ такое нелинейное взаимодействие компонент обеспечивалось их взаимодействием с носителями скалярных зарядов. Эта модель, однако, обладает некоторыми недостатками, – во-первых, чрезвычайной математической сложностью, затрудняющей её аналитическое исследование, а, во-вторых, недостаточно убедительной физической аргументацией появления на ранних стадиях космологической эволюции скалярно заряженных фермионов.

В связи с этим возникает закономерный вопрос: нельзя ли построить космологическую модель на чисто полевой основе, отражающей основные черты модели со скалярными носителями зарядов? В этой статье мы исследуем такую двухполевую модель скалярного поля с кинетическим взаимодействие между компонентами.

1. Основные уравнения и анализ

Рассмотрим асимметричный скалярный Хиггсов дублет (см., например, [1]) с кинетической связью между компонентами. Соответствующая простейшая функция Лагранжа имеет вид:

L = 16n ^(g i ^{k ф} ， і ^ф ， к - 2^V(Ф)) + 16n ^{( —} g ik ^ф ， і ^ф ， к - ^2v(ф)) + 8П^Ү 卜 ik ^Ф ,2 ^ф ,к) ,             ⁽¹⁾

где

V (ф)

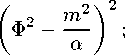
v(ф)

β

φ

µ ²

β

– потенциальная энергия соответствующих скалярных полей, α и β – константы их самодействия, m и 〃 一 их массы квантов, ү - константа кинетического взаимодействия, p >  1 - некоторое целое число. В отличие от [1] в рассматриваемой модели был конкретизирован знак перед потенциалом классического и фантомного полей, отвечающий реальной физической модели.

Переходя к стандартным обозначениям качественной теории динамических систем (см. [13])

dx i dt

Fi(xi, . .. ,Xn); i = 1,n, запишем систему уравнений Эйнштейна и хиггсовых полей в виде:

т2ф - аф3   М2Ф - вФ3 " 口 \ ф = Z (= F1)； Z = —3HZ--—--ү 1 丄 2  (= F2)；

1 + ү ²          1 + ү ²

• —                2 订丄 〃 2Ф — ^вф^{3   т}2^ф — ^аф3 r

^ф = z, (= F3^); z = ^—3Hz +   —―2--^ү—^~~2^ (= F4) ；

1 + ү ²          1 + ү ²

H =    - 2Z ² + уz ² - ү^Zz ( 三 F5).

При этом первый интеграл динамической системы (3) можно записать в виде:

Z ² аФ ⁴ т ² Ф ² z ² вф ⁴    〃 ² Ф ²          .

^{3H 2 -} т ⁺ 丁 - 丁 + е + Т - Т ^- ү^{Zz - Л} = °.

Аналогично [12] можно доказать [14] ряд свойств динамической системы (3), в частности, свойства инвариантности её и характеров её особых точек по отношению к преобразованию подобия фундаментальных параметров, а также асимптотические свойства вблизи космологических сингулярностей.

На Рис. 1 показаны графики эволюции геометрических факторов £(t) и H(t), а на Рис. 2 эволюция скалярных потенциалов Ф( 。 и ф(t) в модели с параметрами (подробности см. в [15]):

P 三 [[а,в,т, 〃 ],ү, Л] = [[°.°1, °.°1, °.1, °.1],1° ^{- 2} ,1° ^-6] ;

I 三[Ф0,Z0,ф0,Z0,e] = [°, °, °.°1, °, 1], (е = ±1), где знак e соответствует выбору положительного или отрицательного решения уравнения (4) относительно начального значения параметра Хаббла.

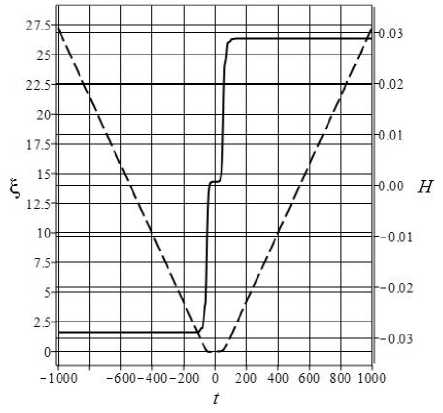
Рис. 1. Эволюция геометрических факторов в модели с параметрами P и начальными условиями I : £(t) 一 штриховая и H(t) 一 сплошная линия.

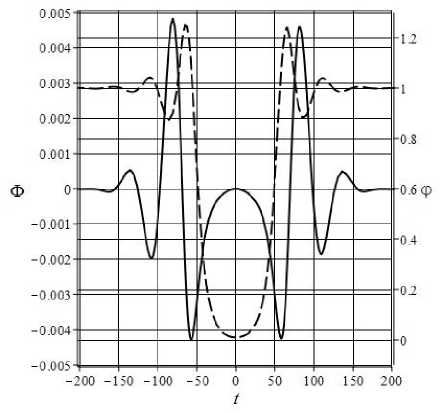
Рис. 2. Эволюция скалярных полей в модели с параметрами P и начальными условиями I : Ф(t) 一 сплошная и ф(t) 一 штриховая линия (крупный план).

Таким образом, в бесконечном прошлом Вселенная стартует из состояния, близкого к особой точке M — +i = [0, 0, +1, 0, - 0.0289] и находится в состоянии инфляционного сжатия. Вблизи точки отскока t b ^ 0 в системе возникают колебания фантомного и классического скалярных полей, после чего система переходит в состояние инфляционного расширения, соответствующего особой точке M ++1 = [0, 0, +1,0, +0.0289], восстанавливая первоначальные значения потенциалов скалярных полей.

В данной модели интервал колебания потенциалов скалярных полей, на котором потенциал классического поля достигает значений порядка | Ф« ь ) | 〜 0.005, а потенциал фантомного поля обращается в нуль, занимает порядка 300 планковских времён. При переходе с помощью масштабного преобразования к реальным величинам фундаментальных констант для масштабов КХД-теории этот период может растянуться до 3 • 104 планковских времен, а для СМ - до 3 • 10 ¹⁵ t pi .

Заключение

Подводя итоги, укажем следующие основные результаты.

• •    Предложена и исследована модель эволюции Вселенной, основанной на асимметричном Хигг-совом скалярном дублете с кинетической связью, пропорциональной произведению производных компонент скалярного дублета. В частности, проведён качественный анализ динамической системы модели, исследованы и доказаны свойства симметрии модели по отношению к преобразованию отражения и подобия.

• •    Выявлены основные типы поведения космологической модели в зависимости от фундаментальных параметров и начальных условий. Выявлены случаи наличия первоначальной и конечной космологических сингулярностей и точек отскока.

• •    Показано, что вблизи точек отскока фантомная компонента φ скалярного дублета генерирует его классическую компоненту Ф.

• •    Доказано аналитически и подтверждено численным моделированием асимптотическое поведение космологической модели вблизи точек начальной сингулярности и Большого разрыва, соответствующее коэффициенту баротропы к = 1 (р = £ ) .

• •    Проведены оценки вероятности рождения фермионных пар в сильном переменном скалярном поле вблизи точек отскока.

Все выявленные особенности космологических моделей, основанных на асимметричном скалярном дублете: наличие начальных сингулярностей, точек отскока и точек большого разрыва, генерация компонент скалярного дублета и др., аналогичны особенностям космологических моделей, основанных на системах скалярно заряженных фермионов [8], что, по-видимому, даёт возможность замены математически сложной модели образования сверхмассивных чёрных дыр [10] – [11] более простой, построенной на чисто полевой основе. Кроме того, важным обстоятельством является также достаточно интенсивное рождение фермионных пар скалярным полем вблизи точек отскока. Благодаря этому фактору необходимое число скалярно заряженных фермионов может быть получено независимо от процессов гравитационного рождения пар, причём на стадии холодной Вселенной.