Космология от Адама и Евы до Алексея Старобинского. Часть 1

Вместо Введения

Зимняя школа. «Петровские чтения» 2018 года, посвящена. 70-летию замечательного ученого академика. Алексея Александровича. Старобипского. Алексей — космолог (хотя у пего есть прекрасные работы и по теории черных дыр) с всемирной известностью. Чуть было не написал вместо «всемирной» - «вселенской», по вовремя спохватился. Ведь 70 световых лет, куда, уже дошел сигнал о рождении Алексея — это всего лишь 21,46 парсек, сравните с мегапарсеками, которыми оперирует космология. II поскольку 70-летие — то самое время, когда, уже можно оглянуться назад, вспоминая весь пройденный (по еще не до конца!) путь, то захотелось и мне оглянуться назад и вспомнить весь путь, пройденный космологией (по еще не до конца!) с самого ее зарождения.

Но начнем мы, все-таки, как и положено в пауке, с определения. Что такое космология? Ответ короток: это наука, о Вселенной в целом. Это значит, что нас интересует Вселенная как единый объект: его структура, (если таковая имеется), какие законы ею управляют, т.е. взаимодействие частей этой структуры; стационарна ли Вселенная или же развивается, а. если развивается, то было ли начало и будет ли конец; размеры Вселенной, т.е. ее объем, конечный или бесконечный... При этом, космологическая теория не должна, иметь внутренние противоречия, т.е. должна быть самосогласованной.

Часть Первая. Доисторическая эпоха

Так с чего же началась космология? Вот вам легендарная история — с Адама, и Евы. Бог создал первого человека, на. Земле, Адама. (= человек земли), по образу и подобию своему. А уже из ребра. Адамова. — первую женщину, Еву (дающая жизнь). И поселил их в Эдеме — земном раю, где всего было вдоволь — «плодитесь и размножайтесь». Но Ева, в отличие от Адама, могла, оказаться и с изъянами. И вот Бог решил это проверить и послал к Еве (к пей!) Змия-искусителя. Именно встреча, первых людей со Змием-искусителем изображена, на. картине Лукаса. Кранаха. Старшего, написанной в 1513-1515 годах и висящей в Майиско-Фраикоиском музее в Вюрцбурге.

Змий точно распознал — Ева. любопытна. И предложил вкусить плод Древа. Познания. Напрасно Бог сулил им обоим всяческие кары: изгнание из рая, добывание хлебы насущного в поте лица, а. Еве еще и рождение детей в муках — она. не устояла. Кстати на. одной из более поздних картин Кранаха, с таким же сюжетом Ева. протягивает Адаму первое яблоко (опа. ведь плоть от плоти - ребро) и тянется за. вторым. А он озадаченно чешет голову: то ли взять, то ли пет. Адам, возможно, и устоял бы перед Змием, а. перед Евой — не смог. А здесь, смотрите (!), он уже держит первое яблоко, в левой руке у Евы — второе, и опа. тянется за. третьим. Вот! Это та. самая «изюминка», которая определила, мой выбор именно этой картины из множества, других. Третье яблоко и есть неутолимая (!) жажда, познания, невзирая на. тяжелый труд и муки. Это — начало всех паук, в том числе и космологии.

Легенда, легендой, а. как же могла, быть на. самом деле?

Вопрос: что для наших очень далеких предков представляла. Вселенная? Ответ прост: Космос = небо. А что па. небе? Солнце днем, Лупа, и звезды ночью. Все очевидно. Круговерть происходит вокруг Земли, па. которой живем Мы. Вот и все. Любопытство и жажда, познания вполне удовлетворены. А ночью надо спать — днем трудились до седьмого пота, добывая пропитание. Но для некоторых как раз и было работой — не спать ночью. Это — древние пастухи, ночные сторожа. В ясную ночь звезды сияли завораживающе ярко. Городской подсветки не было и в помине. И они пристально вглядывались в небо. Их двигала, вовсе не жажда, познания. Задача, была, более прозаическая — «не заснуть!». Поэтому пастухи-сторожа, объединяли яркие звезды в созвездия, давали им названия, придумывали, для запоминания, различные истории, отголоски которых, возможно, дошли до нас в виде мифов. В результате они дали небу «ординату», т.е. навели порядок, и это была, видимо, первая карта, звездного неба, пока, еще устная. Думаю, опа. долго еще исправно служила, в качестве надежного ориентира, не только в пространстве, по и во времени (к примеру, «разбуди меня, когда. Кассиопея будет вон над тем деревом»), И вдруг — кто-то их пих, обладавший, вероятно, обостренным зрением хищника, чутко реагирующим на. малейшие движения, заметил, что одна, из звезд перемещается, день ото дня, между другими. И он сумел передать эту информацию своим товарищам, четко указав ее небесные координаты. Мало-помалу обнаружились еще три, всего четыре. Теперь они известны нам под именами Вейера, Марс, Юпитер и Сатурн. Полагаю, наши «открыватели небес» ясно понимали, что эти «небесные странники» находятся ближе всех остальных звезд, поскольку затмевают их. Возможно, так, или примерно так, были открыты планеты. По-гречески, ттАат/туттуф что и переводится как «странник». Был сделан громадный шаг вперед в «разглядывании» Вселенной, которое уже более не представлялась в виде примитивного хоровода, звезд. Несомненно, «наблюдатели-дежурные» заметили еще один признак, отличающий планеты от звезд: звезды мерцают, тогда, как планеты — пет. Стало

интересно. К сожалению, наши герои, в отличие от Адама, и Евы, так и остались безымянными.

Следующий этап, уже сознательного и целенаправленного, изучения доступной тогда. Вселенной связан с кропотливой работой многих поколений египетских жрецов. Вот и соответствующая иллюстрация.

А что это за. шарики, подающие сверху па. жриц и жрецов? Неужели яблоки и древа, познания? Трудно назвать называть этих жрецов космологами, скорее, астрономами. Их не интересовала. Вселенная как объект, они смиренно воспринимали ее как данность (созданную Богом) и усердно цель была, чисто утилитарной : предсказать точные даты разлива. Нила, и начала, «посевной кампании», солнечные и лунные затмения (что было важно для поддержания верховной власти фараонов). Но кажется мне, основное «рабочее время» они тратили на. составление различных гороскопов, прежде всего, для царствующей династии, а. также по заказам, что обеспечивало «спонсорскую поддержку». Наука, о звездах и планетах (в числе последних были также Солнце и Лупа.) получила, государственный статус и успешно развивалась.

Я далек от мысли, что жрецы и жрицы лишь измеряли и тупо записывали результаты па. свитках папируса. Уверен, что они заметили и годичные циклы в изменении положения звезд и планет, и собственные периодичности в движении планет (для каждой — свои). Не говоря уже о суточном

Эстафету египетских жрецов подхватили жрецы вавилонские. Цели их астрономических наблюдений были те же: календарь и гороскопы. Важно, что это продолжалось много веков. В результате накопилось много данных, и была, достигнута, очень высокая точность измерений. Как и в Древнем Египте, астрономы были обласканы государством, в частности, царем Хаммурапи. Во всех городах были построены башни-обсерватории. Жрецам-астроиомам были известны планеты Меркурий, Вейера, Марс, Юпитер, Сатурн — естественно, под другими именами. Наверняка, они видели и Уран, по принимали его за. тусклую звезду. Достижения вавилонян оказали большое влияние на. астрономию в Древней Греции, когда, стали доступны последним после завоеваний Александра. Македонского. Космология же как наука, о Вселенной в целом, в Древнем Вавилоне была, весьма, примитивна: Земля плоская, есть океан, есть подземный мир и есть Небо (причем их аж три штуки).

Громадный шаг вперед в познание Космоса, сделали древние греки. Необходимо отметить, что этому способствовало и общественное устройство — система, полисов, т.е. городов-государств. Стали появляться, причем во множестве, «свободные мыслители» - мы назвали бы их учеными (в отличие от Древнего Египта, и Древнего Вавилона, где, конечно же, жрецы тоже были учеными, по, все-таки, по должности, а. не исключительно по призванию). И основной целью этих ученых было именно познание мира, вокруг. Нас сейчас интересует их вклад в космологию, которая в это время уже полностью отождествлялась с астрономией.

Так на что же подвигла мыслителей муза астрономии Урания ( Oupcvtc, устремленная к небу)

Самое цепное — это, конечно, геометризация Вселенной. Известна очень крайняя точка зрения Аристотеля ( АрьсттотеХрО, что Вселенная делится на две части: подлунный мир и надлунный мир. Подлунный мир — это Земля, здесь правит физика, (в тогдашнем ее понимании), одни явления являются следствием других, все перемешано. И никакой математики! В надлунном же мире, т.е. в Космосе, царят гармония и совершенство, это божественные создания. Здесь правит математика. И никакой физики! Но несколькими веками ранее Аристотеля Пифагор ( П.г,9а^ора( (570—490 ВС)) выдвинул предположение о шарообразности Земли, увеличив тем самым «объем» Вселенной вдвое. Наверняка, он руководствовался не только соображениями о совершенстве (что может быть совершеннее сферы или шара!), по и реальными доказательствами шарообразности Лупы: опа. светит отраженным светом Солнца, (это доказывается солнечными затмениями), а. форма, лунных фаз, от топкого серповидного месяца, до полнолуния, может быть объяснена, только шарообразностью. А чем Земля хуже? Впоследствии через 200 лет) Эратосфен ( Ератостбеур^ 274—194 ВС)) сумел даже вычислить диаметр Земли.

Требование совершенства, привело к появлению концепции небесной сферы. Поскольку Земля — пуп Вселенной, то равномерное и одинаковое перемещение по небу сразу всех звезд естественно было объяснить вращением некой сферы, к которой намертво прикреплены (какими-то скрепами) звезды. Периодическое годичное угловое смещение (различное для каждой звезды) — годичный параллакс — удалось (ненадежно) измерить лишь в 1837 году Фридриху Георгу Вильгельму (Василию Яковлевичу) Струве в Пулковской обсерватории и в 1938 году (надежно) Фридриху Вильгельму Бесселю в Геттингенской обсерватории.

Известна, древним грекам была, и эклиптика. Открытие зодиакального круга, приписывается астроному и геометру Энолиду Хиосскому ( OlvotlSt)^, жившему в 5 веке до нашей эры.

Что может быть совершеннее равномерного движения по окружности?! Но гармонию портили планеты с их явно неравномерным и порою даже попятными перемещениями. Видимо, это настолько раздражало, что Платон (ПАатшт/ 429-427—347 ВС) поставил задачу описать движения планет сложением (мы бы сейчас это назвали латинским термином «суперпозиция», которого древние греки, разумеется, знать не могли) нескольких равномерных движений по кругу. Я нарочно слово «описать», а. не «объяснить», чтобы подчеркнуть, что причины такого движения никого в то время не интересовали, поскольку планеты считались божествами — недаром им присваивали имена, богов и богинь.

Первым решил задачу Платона Евдокс Книдский ( Еибо^о^ 408—355 ВС). Он предложил теорию «гомоцентрических сфер». Их было 27. В окончательном варианте у Аристотеля их число увеличилось до 54. Но точность предсказаний оставляла, желать лучшего. Особенно «сопротивлялся» Марс. Мы уж не говорим о том, из чего должны были быть «сделаны» такие сферы. Ведь, в отличие от небесной сферы со звездами, за. которой, как думали некоторые греческие философы (чуть было не написал «представляли»), пет вообще никакого пространства, (и это 2500 дет назад — уму непостижимо), сферы Евдокса, должны были быть абсолютно прозрачными, чтобы не задерживать свет от этих звезд. Но вскоре (через каких-то 150 лет) ее сменила, более изощренная и более точная модель эпициклов.

Идея эпициклов была выдвинута Аполлонием Пергским ( AtoXXovlo^ 262—190 ВС ). Предполагалось, что Лупа, и Солнце движутся по неким малым окружностям — эпициклам, центр которых, в свою очередь, движутся по большим окружностям — деферентам, центр последних совпадает с центром Земли.

Эту идею подхватил Гиппарх ( 1ттархо^ 190—120 ВС), который не только развил ее, построив первую дошедшую до пас достаточно точную теорию движения Лупы и Солнца, по и вычислил расстояния до них (в этом он следовал методу, изобретенному ранее Аристархом Самосским, о чем речь впереди).

Для нас особенно важно именно это достижение Гиппарха, поскольку это был прорыв в «третье измерение» в космологии.

Примерно через 250 лет после Гиппарха, была, пакопец-то, создана, первая полная геоцентрическая модель Вселенной. Полная она. потому, что описывает геометрически не только движение Луны и Солнца, по и всех остальных известных тогда, планет с небывалой доселе точностью. А почему Гиппарх этого не смог сделать? Ему помешало так называемое «зодиакальное неравенство». Мы не будем вдаваться в подробности, а. скажем лишь, что не удалось совместить равномерное движение по эпициклу плюс равномерное движение по деференту с данными наблюдений за. планетами. Особенно постарался Марс. Автором этой теоретической модели был Клавдий Птолемей ( КХаибьоС, П тоХе^ьоС ~ 100 ~ 170 AD), живший и работавший в Александрии Египетской.

Птолемей сохранил и эпициклы, и деференты, по отказался от равномерности движения он деференту. Более того, он «убрал» центр деферента, из центра. Земли. В его теории движение планет только выглядит равномерным, если смотреть из особой точки, называемой эквантом и расположенный симметрично центру Земли относительно центра, деферента. Эта. конструкция получила. название «бисекция эксцентриситета». Фактически, Птолемей увеличил число параметров теории, что и позволило добиться успеха.

Очень изящная геометрическая игрушка! Но как такое могло прийти в голову, ведь отказ от равномерности движения — очень и очень радикальный шаг? Насчет головы Птолемея — не знаю и знать не могу, по в мою голову пришла, вот какая гипотеза. Я уже упоминал о том, что в древности планеты считались божествами, в честь которых им и давались имена. Так вот, а. что если это не сами божества, а. лишь их образы? Тогда, планеты вовсе не обязаны двигаться равномерно по окружностям — главное, чтобы нужные божества, видели это движение равномерным из той точки. В которой они сами находятся. Это и есть эквант, и он просто должен быть расположен не па. Земле.

Основной труд Клавдия Птолемея был издан первоначально примерно в 140 году под названием «Математическое собрание в 13 книгах» ( Мабтщатькьк^С ^wt ахеш С), затем на него ссылались как «Великая книга» и «Величайшее сочинение» ( Мермуту, мэгистэ). В арабском переводе это превратилось в «Ал маджиста», а. в последующем переводе уже с арабского па. латынь в «Альмагест». Под этим названием мы знаем его и сегодня. Теория Птолемея царствовала, почти 13 веков.

Но в XIV веке арабские астрономы подвергли ее критике за. отказ от равномерного движения. Видимо, девиз был «Аллах так повелел». Но им все равно требовались новые параметры. Поэтому в модель были введены новые эпициклы, центр которых двигался по «старым» эпициклам. В обоих вариантах (птолемеевском и арабском) теория продержалась еще два. столетия. Вообще, паука, арабского мира, и не только астрономия (= космология) продолжила, славные традиции древнегреческих ученых, умножила, их достижения и донесла, все это до Средневековой Европы, не позволила, им пропасть втуне.

Итак, приближается XVI век, когда, в геоцентрической картине Вселенной появилась первая серьезная трещина. А пока. — полное торжество этой чисто математической (= геометрической) модели. Физикой тут и не пахнет — никто не задумывается над причинами столь сложных движений Лупы, Солнца, и планет. Для практических нужд — календарь, гороскопы, предсказания затмений — хватает, и ладно. Мне представляется, что теория Птолемея, и особенно ее арабский вариант (логически более экономный) напоминает своеобразную геометрическую теорию возму- щепий: повысилась точность измерений — введем в модель еще один эпицикл. И все тут, что еще вам надобно? Окончания же эры геоцентризма, придется ждать вплоть до конца XVII века, когда, появятся законы Кеплера. А пока, чтобы скоротать ожидание, вернемся снова, в Древнюю Грецию, примерно на 2300 лет назад. Нас интересует Аристарх Самосский (Арьсттархо^ о ^арьо( ~ 310 ~ 230 ВС), который родился на острове Самос (там же, где и Пифагор двумя с половиной столетиями раньше)

Чем же он знаменит? Он умудрился (от слова, «мудрец»), наблюдая за. солнечными и лунными затмениями, рассчитать радиусы Солнца, и Луны в единицах радиуса. Земли, полагая, следуя Пифагору, что Земля, как и Лупа, и Солнце, шарообразна, (это было еще до открытия, сделанного Эратосфеном) и оцепить расстояния до этих светил. Впоследствии Гиппарх воспользовался таким же методом и сделал все гораздо точнее. Но для истории космологии важнее то, что Аристарх Самосский, убедившись в громадности Солнца, по сравнению с Землей, усомнился, что столь тяжелое тело вращается вокруг столь малого. А это уже, согласитесь, не математика, а. физика! Он выдвинул гипотезу, что истинным центром мира, является Солнце, а. вот Земля вращается вокруг пего с периодом в 1 год и вокруг своей оси с периодом в 1 сутки. Звезды же, ввиду пепаблюдаемости в то далекое время годичного параллакса, Аристарх Самосский отправил туда, «куда Макар телят не гонял», т.е. па бесконечность. Это была первая в истории гелиоцентрическая картина, мира, (кстати, приоритет Аристарха. Самосского признавали и Галилей, и Кеплер). А что же было дальше? А дальше посыпались обвинения в безбожии и пеблагочестии и угрозы привлечь к суду. В то время к такому относились чрезвычайно серьезно, и великолепная (уже не просто математическая) гипотеза, была, прочно забыта, па. 1800 лет!

В начале XVI века, молодой польский астроном (+ математик — механик — общественный деятель — каноник) Николай Коперник (Mikolai Kopernik 1473—1543) начал работать над книгой всей своей жизни «Об обращении небесных сфер».

Работа, продолжалась почти 40 лет, а. книга вышла, из печати чуть ли не в день его смерти. Николай Коперник возродил идею Аристарха. Самосского о Солнце как центре мироздания. Но теперь это уже не просто гипотеза, основанная па. недоумении — как может большое Солнце обращаться вокруг маленькой Земли? Главным достижением Коперника, было очень простое и изящное объяснение попятных движений планет — явления, причинявшего столько хлопот геоцептристам па. протяжении как минимум двух тысячелетий и заставлявшего их все усложнять и усложнять свои теории. Возьмем, к примеру, Марс. Все дело в том, что и Земля, и Марс вращаются вокруг Солн ца. в одном направлении, по с различными периодами. Поэтому планеты оказываются то по одну сторону от Солнца, то по разные стороны. В первом случае видимое с Земли угловое перемещение Марса, происходит быстрее, чем угловое перемещение, видимое с Солнца, (из центра, мира), а. во втором случае — наоборот, медленнее. Земля просто-напросто перегоняет Марс. И так со всеми остальными планетами. В результате, оказывается совершенно ненужным первый, основной, эпицикл геоцентрических моделей. Заметим, между прочим, что попятное движение должно происходить именно ночью, что и позволило наблюдать его в древности.

Несомненно, это величайшее открытие. И дело здесь не только и не столько в значительном упрощении вычислений, а в том, что найдена единственная причина однотипных явлений. Это — начало абсолютно нового научного подхода. Не просто описание, а поиск причин. Уже не просто математика, а самая настоящая теоретическая физика, пусть пока только кинематика.

Еще одно, несомненно, серьезнейшее достижение гелиоцентрической модели: она позволяет вычислить отношения расстояний от планет до Солнца, что абсолютно невозможно в геоцентрической картине. Но насколько это важно, станет ясным лишь впоследствии.

К сожалению, теория, представленная Николаем Коперником, была далека от совершенства и не столь убедительна, как нам бы хотелось. Он оставил в неприкосновенности небесные сферы ( о чем свидетельствует само название книги) и равномерность движения планет по окружностям. Результат — все-таки пришлось использовать и эпициклы (хотя и не основные), и деференты. И это основная причина того, что «новая» гелиоцентрическая модель не была принята с криками «ура» не только клерикалами, но и современным Копернику научным сообществом. Пришлось ждать 21 год рождения Галилео Галилея (Galileo Galilei 1564— 1642).

Галилео Галилей появился на свет в 1564 году в славном городе Пиза. К его рождению многое было готово. Уже вышла из печати книга Николая Коперника. Уже была знаменитая башня, которая начала падать еще в процессе возведения, но, тем не менее (как будто специально) была достроена.

Нет нужды пересказывать здесь биографию Галилея. Но необходимо отметить, что это был богато одаренный юноша: музыка, рисование, а из чтения его (будущих) книг ясно, что имелся еще и литературный талант. В 17 лет он поступил в Пизанский университет на медицинское отделение (по настоянию отца), но страстно увлекся математикой, которой до того совершенно не знал. В университете Галилей прослыл неукротимым спорщиком. И, возможно, именно там он познакомился с гелиоцентрической теорией Коперника. Через 3 года Галилей вынужден был покинуть университет из-за финансовых трудностей в семье. Но, по счастью, он уже был знаком с образованнейшим, богатым и влиятельным любителем науки маркизом Гвидомальдо дель Монте, который обеспечил и его дальнейшую учебу, и, впоследствии, место профессора в этом же университете. Дело здесь в том, что юноша уже прославился остроумным изобретением гидростатических весов, что позволило маркизу написать: «Со времен Архимеда мир не видел такого гения, как Галилей». Но нас интересуют научные достиже

ния.

Галилео Галилей по праву считается родоначальником экспериментальной физики (и, вообще, экспериментальной науки).Своими опытами по скатыванию тел по скользкой наклонной плоскости (проделанные в бытность им профессором Падуанского университета) он доказал несостоятельность утверждения Аристотеля о естественности состояния покоя, открыв тем самым закон инерции, обосновав в своих «Диалогах» этот закон еще и мысленными экспериментами. Ныне он знаком всем как 1-й закон Ньютона.

Галилео Галилей по праву считается родоначальником теоретической физики, применив математику для расчетов различных движений. Он первым произвел полный анализ движения тела, брошенного под углом к горизонту, в однородном поле тяжести и доказал, что его траектория — парабола. Для этого ему пришлось предположить, что такое движение можно рассматривать как составное, т.е. как суперпозицию горизонтального движения по инерции с постоянной скоростью и равноускоренного движения по вертикали. Этот принцип суперпозиции был впоследствии использован Ньютоном при формулировке 2-го закона: скорость есть вектор, ускорение есть вектор, сила, (как причина, ускорения) есть вектор.

Галилео Галилей по праву считается родоначальником гравитационной пауки. Бросая различные тела, с наклонной Пизанской башни (а, может, он и не бросал, по легенда, так хороша.!), установил, фактически, пропорциональность гравитационной и инертной масс, что потом получило название «принцип эквивалентности» и легло в основу общей теории относительности (релятивистской гравитации), созданной Эйнштейном.

Все эти принципиальные открытия Галилея оказались чрезвычайно важными для создания величественного здания механики, а. следом за. пей и всей теоретической физики, включая, разумеется, и все теоретические космологические модели. Уже этого было бы достаточно для любого ученого. Но одно из его деяний имеет к астрономии и космологии самое непосредственное отношение. Это — ТЕЛЕСКОП. Галилей не был изобретателем телескопа, они уже были известны, назывались «голландскими трубами» и использовались для подглядывания в окна. Но он оказался первым, кто направил телескоп в небо (возможно, лишь одним из первых, по точно первым, кто об этом написал и опубликовал (!) результаты наблюдений). А результаты, по тем временам, были потрясающими. Это и обнаружение гор и кратеров на. Лупе, пятен па. Солнце, доказательство вращения Солнца, вокруг своей оси, и фазы Вейеры. Но для пашей темы — космологии (все еще = астрономии) — важны три из них. Первое: диски планет увеличиваются при наблюдении во все более мощные телескопы, а. вот диски звезд — пет. Что, кстати, не объясняет мерцание звезд, по объясняет немерцание планет. Вывод Галилея: планеты находятся гораздо ближе, чем звезды, последние же он, следуя логике гелиоцентрической системы мира, удаляет «па. бесконечность», как и Аристарх Самосский. Но в геоцентрической модели звезды могут безмятежно продолжать существовать в качестве «божественных светильников», не подчиняясь никаким земным законам. А вот второе «космологическое» открытие завзятым геоцентристам объяснить уже гораздо труднее. Галилей обнаружил, что Млечный путь состоит из множества, звезд. А это уже — структура, и потому нелегко представить, зачем нужно было ее создавать для «божьих светильников». Третье, и, на. мой взгляд, самое главное — открытие четырех спутников Юпитера, известных нам сейчас под именами Ио, Каллисто, Европа, и Ганимед. Это было не просто: подошел к телескопу и .. далее, как Юлий Цезарь, Veni, Vidi, Vici («пришел, увидел, победил». Потребовалось полтора, года, прежде чем Галилей окончательно удостоверился, что новые лупы обращаются именно вокруг Юпитера. И теперь уже невозможно утверждать, что буквально все вращается только вокруг Земли, и трудно также поверить в существование небесных сфер.

Широкой общественности Галилей известен, прежде всего, конфликтом с католической церковью и преследованиями со стороны инквизиции, как «борец» за. «истинную» гелиоцентрическую модель Коперника, против «ложной» геоцентрической модели Птолемея. В действительности, Галилей не нашел прямых доказательств вращения Земли вокруг Солнца, (как уже упоминалось, таковым могло быть только обнаружение годичных параллаксов звезд), по привел столько косвенных аргументов, что теория Коперника, была, принята, многими современными ему учеными. Для самого же Галилея, похоже, истинность гелиоцентризма, не подлежала, сомнениям — он был заворожен простотой и изяществом объяснения возвратных движений планет с единой точки зрения. Очевидно, что несложно придумать миллион теорий для объяснения одпого-едипствешюго явления, по количество теорий, объясняющих единым образом миллион явлений, существенно меньше.

В то же время, что и Галилео Галилей, жил и, главное, работал великий ученый, влюбленный в астрономию, Тихо Браге (Tyge Ottesen Brahe 1546—1601), вначале в Дании, где он основал несколько обсерваторий на. островах, а. в конце концов — в Праге.

Мы не будем перечислять здесь его неисчислимые заслуги перед астрономией. Но вот главная заслуга, перед космологией — это приглашение молодого тогда, и одаренного Иоганна. Кеплера. (Johannes Kepler 1571— 1630) для математической обработки своих результатов наблюдений за. планетами.

Кеплер проделал неимоверную работу, тщательно изучил наследие Тихо Браге и вывел три, ставших знаменитыми, закона, движения планет. И недаром па. памятнике в Праге они стоят рядом, Тихо Браге и Иоганн Кеплер.

Вот эти три замечательные законы:

• I.    Планеты двигаются по эллипсам, в одном из фокусов которых находится Солнце.

• II.    Радиус-вектор каждой планеты заметает равные площади за. равные промежутки времени.

Любопытно, что второй закон был сформулирован Кеплером даже раньше первого. Возможно, что именно это позволило ему «угадать» первый закон. Думаю, необходимо отметить следующее важное обстоятельство. Несмотря на. то, что формулировка, первых двух законов указывает, как бы, па. гелиоцентрическую картину мира, они, на. самом деле, нисколько не противоречат геоцентрической картине, если вот это самое «как бы» вставить прямо в первый закон: «Планеты как бы двигаются по эллипсам ... ». Получается, что гелиоцентрическая теория может рассматриваться не более как красивый математический прием, позволяющий значительно упростить вычисления, а. вот «истина» - за. Птолемеем, па. чем и настаивала, церковь.

Оба закона прекрасно иллюстрируются па следующей картинке:

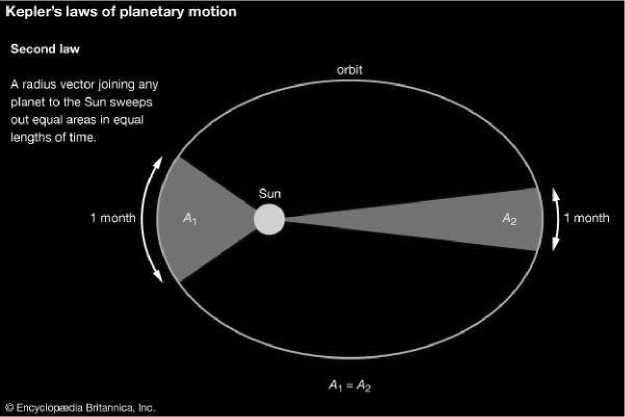
При любой из этих формулировок справедлив третий закон.

• III.    Квадраты периодов обращения планет пропорциональны кубам больших полуосей эллипсов их орбит.

В отличие от первых двух, третий закон сравнивает разные планеты и находит в их движении общие черты, что говорит об общей причине сходства, траекторий. Да. и относительные расстояния планет от Солнца, можно найти, лишь приняв гелиоцентрическую систему. Более подробный анализ мы отложим «па. потом», а. пока, отметим лишь, что законы эти, во-первых, эмпирические и, во-вторых, кинематические, т.е. без указания причин такого, а. не другого, движения. Именно поэтому они и не позволяют сделать выбор между Птолемеем и Коперником.

Иоганн Кеплер был, несомненно, приверженцем теории Николая Коперника. Но при этом вовсе не «слепым» последователем. Он сделал радикальный шаг вперед — отказался от сфер и окружностей. Эллипс — всего-навсего небольшое обобщение окружности, по каков эффект! Уже пет нужды требовать «естественной» равномерности, т.е. постоянной по величине скорости — го раздо естественнее неравномерность, по при этом есть определенная закономерность, выраженная вторым законом. Математически не менее изящная, чем в оригинальной модели Коперника. Все резко упростилось. Вдобавок, еще и третий закон, намекающий на. общую причину движения планет. Очень научно, в духе проповедуемого Галилео Галилеем научного метода. Потому-то и кажется странным, что именно Галилей не принял теорию Кеплера. Возможно, из-за. явного отказа. от окружностей и равномерности. Для Галилея равномерность движения было основным в его формулировке закона, инерции, причем, похоже, под таковым он понимал не только равномерное прямолинейное движение (как учили в школе), по и равномерное движение по окружности.

Галилео Галилей умер 8 января 1642 года. А 25 декабря 1642 года, родился Исаак Ньютон (Issac Newton 1642-1727).

Король умер, да. здравствует король!

Общеизвестно, что Исаак Ньютон был гением. Сам он говорил о себе: если я и видел дальше других, то только потому, что стоял па. плечах гигантов. Ньютон имел в виду Галилео Галилея, Репе Декарта, и Иоганна Кеплера. Мы уже говорили, что Галилей справедливо считается родоначальником теоретической физики. А вот Ньютон — первый физик-теоретик. А чем занимается теоретическая физика. — описанием Природы (= Вселенной). Восхищенный Кеплером, молодой Исаак Ньютон хочет найти природу движения планет по эллипсам. Восхищенный Галилеем и Декартом, он хочет создать «теорию всего», по не словах (философия), а. дать строгое, основанное на. аксиомах, как геометрия в «Началах» Евклида, математическое описание, позволяющее производить конкретные вычисления. Недаром же его основной труд, увидевший свет в 1687 году, назывался «Математические начала, натуральной философии» (т.е. физики).

Здесь уместно вспомнить еще одного гиганта, труды которого оказали огромное влияние на. молодого Ньютона. Это его современник Христиан Гюйгенс (Christian Huygens 1629—1695)

Именно он разработал кинематику криволинейного движения и вывел формулу для центростремительного ускорения a _cf = v²/r, ныне знакомую каждому старшекласснику. По сути, Гюйгенс доказал, опираясь па. открытый Галилеем принцип суперпозиции движений ( то бишь, векторного сложения скоростей), что равномерное движение по окружности является частным случаем общего криволинейного движения (а. не чем-то особенным, в противовес Галилею).

В результате, Ньютон так сформулировал свой первый постулат (в русском переводе): «Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока, и поскольку оно не принуждается приложенными силами изменить это состояние». Как видим, к формулировке Галилея добавлено только одно слово — «прямолинейное» - по опо-то и расставляет все по местам. Постулаты, как и приказы, не обсуждаются. И, если слово «тело» заменить на. «материальная точка», а. слово «сила» - на. «воздействие со стороны других материальных точек», то звучит вполне современно. А как узнать, что сил не действуют? А очень просто, ответил бы Ньютон. Оглянись вокруг себя: не видишь — значит, пет. Системы отсчета, (часы — линейки), связанные с таким телом, мы сейчас называем инерциальными.

Второй постулат (опять же, в формулировке Ньютона и в русском переводе) гласит: «Изменение количества, движения пропорционально прилагаемой внешней движущей силе и происходит по направлению прямой, по которой эта. сила, действует». Количество движения — это то, что мы сейчас называем импульсом (материальной точки), р = mH. Кт — тот самый коэффициент пропорциональности или, иначе, инертная масса, мера, инерции. Что важно — это то, что, в силу принципа, относительности (первого постулата), масса, не зависит от скорости, и для каждого данного тела, (материальной точки) величина, постоянная. В таком виде этот второй закон справедлив только в инерциальных системах отсчета. Что еще он говорит о природе внешних сил, помимо того, что опи описывают взаимодействие с другими телами? А то, что сила, есть вектор, и взаимодействия с разными телами просто складываются. Попятно, что второй закон (= постулат) очень конструктивен: проводя эксперименты с одним и тем же телом, можем сравнивать различные силы с неким эталоном, а. производя эксперименты с одной и той же силой, по с различными телами, можем сравнивать их массы с неким эталоном.

Наконец, третий постулат дает нам очень важную информацию о силах. Вот формулировка. Ньютона: «Действию есть всегда, равное и противоположное противодействие, иначе — взаимодействия двух тел друг на. друга, между собой равны и направлены в противоположные стороны». Этот третий постулат дорогого стоит. Он ведь означает, что сумма, импульсов всех тел изолированной системы сохраняется, т.е. не зависит от времени. С одной оговоркой — импульсы эти измеряются в некоторой инерциальной системе отсчета, (второй закон Ньютона). В частности, мы всегда, можем выбрать такую инерциальную систему отсчета, в которой полный импульс равен пулю, т.е. изолированная система, как целое, покоится. Мы называем ее система, центра, масс. Из равноправия всех таких систем следует незамедлительно, что пространство однородно и изотропно (вот так!). И Исаак Ньютон постулирует эти свойства, предлагая принять существование абсолютного пустого, однородного и изотропного пространства. Добавим к этому, в котором действует геометрия Евклида. А какая же еще? Другие варианты (трехмерная сфера, постоянной положительной кривизны или трехмерный гиперболоид вращения постоянной отрицательной кривизны) тогда, и представить было невозможно. Но для измерений длин, скоростей и ускорений необходимо сравнивать и промежутки времени в разных инерциальных системах отсчета. Как быть с ним? Деваться некуда, и Исаак Ньютон постулирует существование абсолютного однородного времени, текущего совершенно одинаково во всех инерциальных (и не только инерциальных) системах отсчета.

Все! Построение аксиоматической внутренне непротиворечивой «теории всего» завершено. А какое это имеет отношение к космологии? Самое прямое. Постулаты о пространстве и времени — это уже космология. Кроме того, Ньютон создал мощнейший инструмент — математический анализ — для работы с криволинейными траекториями и мог теперь запяться вычислением силы, которая заставляет по (Кеплеру) планеты двигаться вокруг Солнца. То, что из этого вышло, называется теперь законом всемирного тяготения.

История этого открытия полна, драматизма. Ее участники — Исаак Ньютон, Роберт Гук (Robert Hooke 1635—1703) и Эдмунд Галлей (Edmond Halley 1656—1742).

Вкратце: в 1679 году Роберт Гук написал письмо Исааку Ньютону, сообщая, что он пытался вычислить силу притяжения планет к Солнцу, представив движение по эллипсу в виде суперпозиции свободного падения и движения по инерции по касательной, по не преуспел. В этом же письме содержалось предположение, что сила, притяжения должна, быть обратно пропорциональна квадрату расстояния до Солнца. Гук предлагал Ньютону вместе продолжить исследование. В ответном

письме Ньютон наотрез отказался от сотрудничества, и сообщил, что он тоже получил приближенный результат с обратным квадратом, по гораздо раньше. Ни тот, пи другой эти результаты не опубликовал. Тем бы все и закончилось. Но тут вмешалось Провидение в виде двух ярких комет 1680 и 1682 годов. Это побудило английского астронома. Эдмунда. Галлея запяться вычислением орбит этих, а. также большого числа, гораздо более ранних комет. Обнаружив близость траекторий некоторых из них к траектории кометы 1682 года, он сделал очень смелое предположение, что это одна, и та. же комета, вращающаяся, как и планеты, вокруг Солнца. Попутно он также переоткрыл приближенный закон обратных квадратов в 1984 году) и обратился к Гуку и Ньютону за. разъяснениями. Оба ответили, что уже получали подобный результат и пришлют ему точные расчеты. Так вот, Исаак Ньютон прислал, а. Роберт Гук — пет. Галлей с ходу оцепил результаты Ньютона и уговорил того срочно написать книгу, которая будет издана. Королевским обществом (Британской академией паук). Стараниями Эдмунда. Галлея книга, была, напечатана, за. его счет) в 1687 году. Вот так мир получил знаменитые «Математические начала, натуральной философии» (Philosophiae Naturalis Principia Mathematica).

Повторим здесь «неправильный» вывод с правильным результатом. Предположим (вслед за. Ньютоном и Гуком), что планета, движется по окружности, в центре которого находится Солнце. Итак, нервы закон Кеплера, выполнен, хотя и приблизительно, по с большой точностью. Из второго закона. Кеплера, сразу же следует, что это — равномерное движение. Сила, притяжение, исходящая от Солнца, вызывает центростремительное ускорение, равное, согласно Гюйгенсу, а =

R’

где R — радиус орбиты. Далее все просто:

п =

2ttR "Т"

где Т — орбитальный период. Третий закон Кеплера гласит:

Т ²

R3 = с1, где С1 — универсальная константа, одинаковая для всех планет. Получаем для ускорения:

а =

С 2

R2 ’

т.е. закон обратных квадратов, а С2 — опять же, универсальная постоянная. Сила, действующая на планету (с массой т) со стороны Солнца, равна тС2

~ЙГ '

Но, в силу третьего закона Ньютона, такая же сила действует на Солнце (массы М) со стороны планеты. Поэтому,

_ тМ

F = G^ ■ где G — постоянная, универсальная «во всех отношениях». Почему так? Потому что только в таком виде закона, для силы тяготения ускорение любого тела, не зависит от его массы, что и требуется принципом эквивалентности Галилея. Отметим, что, предполагая Солнце находящимся в центре, мы совершили некоторый подлог, поскольку па. Солнце действуют силы притяжения со стороны планет, поэтому связанная с ним система, отсчета, не является инерциальной. Однако, огромная масса, нашего светила, делает это обстоятельство вполне незаметным.

Так что же сделал Ньютон, чтобы получить «точное» решение?

Во-первых, он исследовал динамику парной системы «Солнце — планета», справедливо полагая, что Солнце важнее всего. Оба тела, он считал материальными точками. Во-вторых, в этой задаче двух тел он нашел инерциальную систему отсчета. — систему центра, масс, в которой вектор полного импульса, равен пулю (сумма, импульсов — сохраняющаяся величина, вследствие третьего закона. Ньютона). И именно начало этой систем отсчета, он поместил в фокус эллипса, «поправив» тем самым первый закон Кеплера. В-третьих, он умудрился (от слова, «мудрый») свести задачу двух тел к задаче движения одного тела, в поле центральных сил, создаваемых неким эффективным телом с приведенной (reduced) массой

M red =

тМ т + М

Напомним, что центральной называется сила, величина, которой зависит только от расстояния между взаимодействующими телами (материальными точками). И, конечно же, следуя Кеплеру, он рассматривал движение в одной плоскости. Теперь-то мы знаем, что в задаче двух тел, помимо закона, сохранения полного импульса, в случае центральных сил, действует еще и закон сохранения вектора, момента, импульса, означающий, что движение происходит в плоскости, перпендикулярной этому вектору. Более того, из этого факта напрямую следует второй закон Кеплера. И, наконец, применив третий закон Кеплера, (соответствующим образом модифицированный, поскольку Солнце теперь уже не в фокусе эллипса), Ньютон доказал, что гравитационное взаимодействие между Солнцем и планетой обратно пропорционально квадрату расстояния между ними.

Учитывая вышеизложенное, вряд ли кто-то осмелится оспаривать авторство Ньютона

А как же легендарное яблоко?

Ведь о нем рассказывал сам Ньютон. Нам представляется наиболее вероятной следующая гипотеза: поскольку точное решение проблем движения двух тел, связанных центральной силой — задача, чрезвычайной сложности, то, видимо, падение яблока, (которое все-таки произошло!) навело Ньютона на. идею универсальности гравитационного взаимодействия ( в наших школьных учебниках он так и называется — закон всемирного тяготения). Более точно, пришло озарение: гравитация не только заставляет планеты двигаться вокруг Солнца, а. Лупу — вокруг Земли, по и паша.

«привычная» сила, тяжести есть тоже гравитационное притяжение к Земле. И это позволяет, «сидя па. пеньке где-нибудь в Разливе» (совсем как Лепин) на коленке быстренько вычислить расстояние от Земли до Луны. Примерно вот так: пусть Мо и

Ro — масса и радиус Земли, соответственно, d — расстояние до Луны, а Т — период ее обращения вокруг Земли. И пусть Луна кружится по окружности, тогда центростремительное ускорение а равно

GMo ^а =  d2

f²    / 2 ~d \ ²

dd =

1 47rd² d = ТрГ ,

откуда.

GM0T ² 4^2

GMo

"RT = 9

Но,

— знакомое всем co школы ускорение свободного падения (вот оно, озарение!). Поэтому

, 3    9Т2R2

• ^d =  4^2 '

Подставляя сюда, численные значения (измеренные на. Земле!), получаем замечательно точный результат d ~ 380000 км. Что Ньютон и сделал. Но, к несчастью, он сравнил этот ответ с ошибочным значением, полученным Галилеем, и так расстроился, что отложил публикацию своего главного труда, на. долгие годы. И если бы не Эдмонд Галлей...

А что же космология?

Вслед за. Галилеем, астрономы строили все более мощные и совершенные телескопы. И видели всюду все больше и больше звезд. Вот стихотворение Михайлы Васильевича. Ломоносова. — «сочинение на. заданную тему» (1743 г.):

Открылась бездна, звезд полна;

Звездам числа, пет, бездне дна.

О вы, которых быстрый зрак

Пронзает в книгу вечных прав,

Которым малый вещи знак

Являет естества, устав,

Вам путь известен всех планет;

Скажите, что нас так мятет?

Сомнений полон ваш ответ

О том, что окрест ближних мест.

Скажите ж, коль пространен свет?

И что малейших дале звезд?

Несведом тварей вам конец?

Скажите ж, коль велик творец?

И хотя это было написано уже после смерти Ньютона, вопросы, как видим, остались.

Посмотрим, какова, должна, быть Вселенная по Ньютону.

Во-первых, уже тогда, было ясно, что Земля — вовсе не пуп мироздания, звезды распределены в среднем равномерно и одинаково по всем направлениям, а. все вместе это означает однородность и изотропность. Итак, Вселенная однородна, и изотропна. — то, что мы сейчас называем Космологическим Принципом. Это — первый краеугольный камень и современной космологии (только масштабы, на. которых такое начинает проявляться, сильно увеличились).

Во-вторых, Вселенная, как целое, стационарна.

В-третьих, каковы ее размеры? Конечна, она. или бесконечна?

Ответ Ньютона — Вселенная бесконечна. И это не просто его точка, зрения. Есть и доказательство. Дело в том, что Ньютон открыл то, что мы сейчас называем гравитационной неустойчивостью. Если где-нибудь случилась флуктуация плотности вещества, выше средней, то к тому месту будет сильнее притягиваться материя из соседних областей, и флуктуация начнет расти. Если бы Вселенная имела, конечные размеры, то в результате она. давным- давно схлопнулась бы в одну точку с бесконечной плотностью, ведь у нее позади вечность (стационарность!). Поскольку это явно не так, то Вселенная должна, быть бесконечной!

С бесконечной и стационарной, однородной и изотропной Вселенной все не так уж безобидно. Возникают трудности. Одна. из них и парадокс Ольберса.

Он ярче всего формулируется в виде вопроса: «Почему ночью небо темное?» Представьте себя в центре шара, разделенного па. топкие слои равной толщины, и мысленно вырежьте некий конус, вершина, которого — это Вы. Чем дальше от Вас слой, тем меньше света, получаете от каждой звезды — освещенность падает как квадрат расстояния (совсем как сила. гравитации). Но число звезд в слое становится больше — растет пропорционально квадрату расстояния (площадь сферы). Выходит, каждый слой дает одинаковую освещенность. А слоев-то бесконечно много. Результат — бесконечно яркое небо ночью. От этой «грубой» бесконечности легко избавиться, вспомнив, что звезды — не точки, а. видимы в виде дисков. Поэтому лучи от очень дальних слоев будут непременно утыкаться в эти диски. Но расчеты показывают, что и тогда, небо ночью должно быть «ярче тысячи солнц». Что здесь не так?

Есть и еще одна, неувязка. И во времена. Ньютона, и сейчас совершенно очевидно, что Вселенная как целое, т.е. на. космологическом уровне, управляется гравитацией. Но вот незадача — если на. материальную точку в центре (который может быть выбран произвольно) действует сила, притяжения со стороны некой другой материальной точки, то в бесконечной и стационарной, однородной и изотропной Вселенной всегда, найдется другая точка, диаметрально противоположная первой, которая будет с той же силой тянуть ее в обратную сторону. Результат — среднее «космологическое» гравитационное взаимодействие просто равно пулю. Мы можем пойти еще дальше, поскольку после Ньютона прошло уже 300 лет. Именно, центральное взаимодействие означает, что гравитационные силы — потенциальные, т.е. могут описываться скалярной функцией ..., а. сила, есть градиент этого потенциала, со знаком «минус». Градиент — вектор с компонентами в виде частных производных по координатам. Закон всемирного тяготения Ньютона может быть записан в дифференциальной форме в виде так называемого уравнения Пуассона:

Ар = 4-kGp, где А — дифференциальный оператор Лапласа, куда входят только производные от потенциала, а р — плотность гравитирующего вещества. Нулевое значение «космологических» гравитационных сил означает, что потенциал всюду одинаков, р = const, поэтому в левой части уравнения мы получаем ноль. А вот в правой части р = ро = const = 0.

Вывод: решения вовсе никакого пет!

Но Вселенная существует!

Что здесь не так?

Авторы

Березин Виктор Александрович, д.ф.-м.п, старший научный сотрудник, Институт ядерных исследований РАН, проспект 60-летия Октября, 7а, В-312, г. Москва, 117312, Россия.

Просьба ссылаться на эту статью следующим образом:

Березин В. А. Космология от Адама, и Евы до Алексея Старобинского. Часть 1 // Пространство, время и фундаментальные взаимодействия. 2019. № 2. С. 28—43.