Косвенное определение аэродинамического сопротивления при скоростном спуске на лыжах
Автор: Рудаков Р.Н., Галв П.П., Василенко С.В., Шульгин П.В.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (8) т.4, 2000 года.
Бесплатный доступ
При численном моделировании скоростного спуска на лыжах необходимо знать коэффициенты аэродинамического сопротивления, определяющие силу лобового сопротивления и подъёмную силу при движении лыжника в воздушной среде. В литературе указываются лишь диапазоны изменения этих коэффициентов [1]. Численное моделирование обтекания лыжника потоком воздуха в настоящее время представляет чрезвычайно сложную задачу, а прямые измерения аэродинамических сил требует уникального дорогостоящего оборудования. Авторы предлагают методику индивидуального определения коэффициентов аэродинамического сопротивления, основанную на аналитическом решении задачи спуска на лыжах по прямолинейному участку горы и измерении на практике предельной скорости спуска или времени спуска на заданном отрезке трассы. Для этого строятся изолинии предельной скорости и времени спуска в координатах: параметр аэродинамического сопротивления и коэффициент трения лыж о снег. При известном значении коэффициента трения, найденного другими способами, из графиков изолиний можно определить параметр аэродинамического сопротивления индивидуально для каждого спортсмена.
Скоростной спуск, аэродинамическое сопротивление
Короткий адрес: https://sciup.org/146215730
IDR: 146215730 | УДК: 531/534:
Текст научной статьи Косвенное определение аэродинамического сопротивления при скоростном спуске на лыжах
Аналитическое решение задачи спуска на лыжах
Рассматривается модель лыжника в виде материальной точки, на которую действует сила тяжести P, нормальная реакция N, сила трения F, сила лобового сопротивления R и подъёмная сила Q (рис. 1):
P = mg,(1)
F = N,(2)
R = 1 р SCxV2,(3)
Q = 1 р SCyV2,(4)
где m - масса системы лыжник - лыжи, g - ускорение свободного падения, f -коэффициент трения скольжения лыжи о снег, р - плотность воздуха, S - площадь миделя лыжника (площадь проекции лыжника на плоскость, перпендикулярную вектору скорости V ), Сх , C y - аэродинамические коэффициенты лобового сопротивления и подъёмной силы, соответственно.
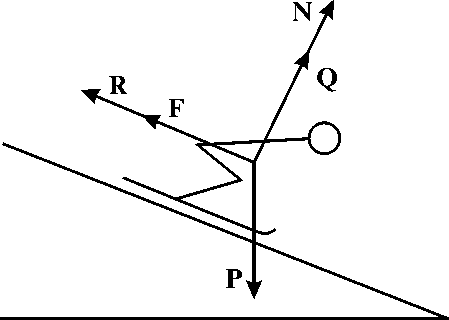
Рис. 1. Силы, действующие на лыжника при скоростном спуске.
На основе II закона Ньютона составляется дифференциальное движения лыжника при его спуске по прямолинейному участку горы:
уравнение
d 2 x dt 2
= g эф (1 - k 2 V 2 ), V = d d x t ,
gэф = g (sin α- f cos α ),
k=
ρµ
^ 2 mgэф ,
µ= S ( C x - fC x ),
где µ - параметр аэродинамического сопротивления движению лыжника.
В работе [2] приводится решение дифференциальных уравнений (5):
V=
x = 2 1 k gэф
1 e 2 kg эф t - 1
k e2kgэфt +1, kgэф t -kgэф t ln(e +2e ) .
При t → ∞ получается формула для предельного значения скорости:
V∞ = k =
2 mg (sin α - f cos α )
,
ρµ
в которую входят коэффициент трения f и аэродинамический параметр µ . Разрешая (7) относительно времени t , получим зависимость t от f и µ :
t = 1 ln( e k 2 gэфx + e 2 k 2 gэфx - 1) (9)
kgэф
Построение изолиний предельной скорости и времени спуска
Изолинии строятся для конкретного спортсмена, для которого надо знать только массу m – массу системы лыжник-лыжи. Угол наклона α считается заданным. При построении изолиний времени спуска пройденное расстояние x фиксировано и считается заданным.
В соответствии с [1] определяем области задания параметра µ и коэффициента трения f : µ = (0.2÷0.8) м2, f = ( 0.0 2 ÷0.08 ).
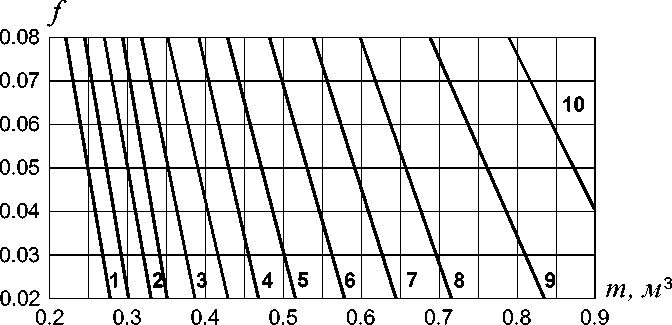
Рис. 2. Изолинии предельной скорости спуска в км/час ( m = 70кг, α = 20o). Прямые 1-10 соответствуют изолиниям с предельной скоростью спуска V ∞ = 130, 120, 110, 100, 95, 90, 85, 80, 75, 70 км/час, соответственно.
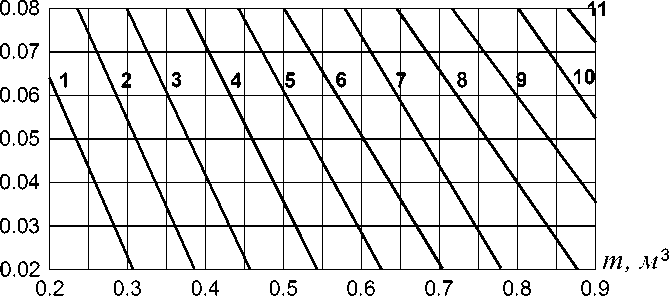
Рис. 3. Изолинии времени спуска в секундах ( m = 70 кг, α = 20o, х = 500 м, V 0 = 0), прямые 1-11 соответствуют изолиниям со временем t = 22, 23,24, 25, 26, 27, 28, 29, 30, 31, 32 c, соответственно.
В этой области параметров по формулам (8) и (9) были составлены таблицы значений V ∞ и t и по ним построены изолинии предельной скорости V ∞ (рис. 2) и времени спуска t по трассе длиной 500 м (рис.3).
Определение параметра аэродинамического сопротивления
Для практического использования графиков изолиний нужно провести серию опытов: измерить предельную скорость спуска V ∞ у данного спортсмена или определить время спуска на заданном участке трассы при начальной скорости, равной нулю. Второй опыт проще, так как для определения предельной скорости надо знать, на каком расстоянии от стартовой линии скорость приближается к предельной скорости. Для оценки этого расстояния приведем з ависимость с корости спуска от расстояния [2]:
V = 1 1 - e - 2 k 2 gэфx , (10)
k из которой находится x. С учётом того, что k= 1 ,
V
∞ получим:
x=
-
V ∞ ln(1 - V 2). g эф V ∞
Так, при α = 20o, f = 0.05, V ∞ = 80 км/час для достижения скорости V = 0.95 V ∞ надо пройти расстояние x = 198.8 м, а при V = 0.99 V ∞ – x = 334.5 м. Заметим, что при V → V ∞ расстояние x → ∞ .
Приведём пример определения параметра µ по изолиниям предельной скорости.
Пусть рис.2 удовлетворяет данным опыта: масса спортсмена m = 70 кг и угол спуска α = 20о. После опытного замера предельной скорости было получено V ∞ = 80 км/час. Коэффициент трения определён из других опытов и составил 0.05.Тогда на рис. 2 по изолинии 80 км/час и значению f = 0.05 находим величину аэродинамического параметра µ = 0.66. Из графика видно, что ошибка в измерении коэффициента трения f не очень существенно влияет на значение искомого параметра. Так, при погрешности нахождения f , равной 10%, погрешность определения аэродинамического параметра µ составляет всего 2%.
Заключение
Разработана методика косвенного определения параметра аэродинамического сопротивления при спуске на лыжах, основанная на использовании графиков изолиний предельной скорости спуска или времени спуска на заданном участке трассы. Этот метод удобно использовать в условиях тренировок, так как графики могут быть составлены для каждого спортсмена и для конкретной трассы в предтренировочный период.


