Краевая задача для смешанного гиперболо-параболического уравнения третьего порядка

Установлены существование и единственность решения одной краевой задачи для смешанного гиперболо-параболического уравнения третьего порядка.

Рассматривается уравнение

( и_хх - Uy + Аш, у > О,

I ^(^ - Uyy + А2иж + А3и), у < О в области Q, ограниченной отрезками ААд, ВВд, АдВд прямых X = 0,X = Y,y = h соответственно и характеристиками АС : X + у = О, ВС : X — у = 1 уравнения (1). Пусть Qi = Q П (у > 0), Q2 = Qn (у < 0), / = (0,1).

Задача 1. Требуется найти функцию и(ж,у) со следующими свойствами:

• I)    и(ж,у) — регулярное решение уравнения (1) в области Q при у ^ 0;

• 2)    U непрерывна, в замкнутой области Q;

• 3)    частные производные U_x,Uy непрерывны в области Лив точках0(0,0) И А(1,0) могут обращаться в бесконечность порядка меньше единицы;

• 4)    U удовлетворяет краевым условиям:

Щ0, у) = Ф1(у), и(1,у) = ф₂(у), Дх, -х^ = ?Ыж), Дх,х- 1) = 'фДх^, (2)

где Ф1, ^,-01,-02 — достаточно гладкие функции, причем

У 1(0) = ^1(0), ф2(0) = ^2(0), ^

Н)=^Н)-

Пусть в начале А2 ^ 0, А3 = 0. В области Q2 общее решение уравнения (1) может быть представлено в виде [1]

и(ж,у) = Дх,у) + ш(у),(3)

где г/(ж,у) — общее решение уравнения

Уст — vyy + Д^$ — 0,(4)

аш(у) — произвольная дважды непрерывно дифференцируемая функция. Без ограничения общности можно предположить

ш(0) = ш'(0) = 0.(5)

Обозначим т(ж) =и(ж,0), у(ж) = ПуДДУ

@ 2002 Елеев В. А., Белхароева. 3. М.

Лемма 1. Если Ai 0 0 п

lim и(ж, 0)^ (ж, 0) = lim и(ж, 0)иДж, 0) = 0, ж->0+                ж-Ы- то для любого регулярного в области Qi решения уравнения (1) справедливо неравенство

1                                 1

j r^x^x = - j УЧхД Xv^dx ^0. о                            о

< Доказательство леммы 1 приведено в [2]. >

Лемма 2. Если п = 0 на ОС U АС, то для любого регулярного в области Q2 решения уравнения (1) справедливо равенство jHa:M^d.,0.

О

• <    Доказательство леммы 2 приведено в [3]. >

Сравнивая (7) и (8) имеем, что т(ж) = 0.

Теорема 1. Пусть и(ж,у) — регулярное решение однородной задачи 1. Тогда tt^x, у) = 0 в Qi.

• <    В области Qi рассмотрим тождество

м(и_жж — Uyy + Aiu) = V^x^x ^{— uu}y ^{— М}ж + ^l^² = 0.

Проинтегрировав его при однородных граничных условиях (2) и т(ж) = 0, получим

(•Дх^

о

dx +

/(^

Qi

— Aiu²) dx dy = 0.

Отсюда следует, что и(ж,у) = 0 в области Qi. В силу равенств Дж,0) = и(ж,0), г/_у(ж,0) = и_у(ж,0), имеем, что Дж,у) = 0 в области Q₂. Из условия Дж,—ж) = —сДу) заключаем, что сДу) = 0 при —| <  у < 0. Следовательно, Дж, у) = 0 в П₂, т. е. Дж, у) = 0 в Q и решение задачи 1 единственно. >

Теорема 2. В области Q существует решение задачи (1).

• <    Из параболической части области Q при у —> 0+, получим задачу

т"(ж) — и(ж) + Ахт(ж) = 0,(9)

т(0)<^1(0), т(0) = р2(0).(10)

Решение уравнения (4), удовлетворяющее краевым условиям

^(ж, —ж) ='01 (ж) — ш(—ж), г/(ж,ж — 1) = 02(ж) — ш(ж — 1),(2')

определяется формулой

^-^ и ^ №) - и ч^и 1111

Задача (9), (10) заменой

т(ж) = г(ж) + ж2 + (<12(0) - уд (0) - 1)ж + уд(0) = г(ж) + Д(ж)

приводится к виду z"(x) + А^ж) = /(ж),                           (12)

г(0)=0,  г(1)=0,                          (13)

где /(ж) = и(ж) — Д(ж) — 2. Решение задачи (12), (13) имеет вид

г(ж) = У G(x, t, Xi)f(t) dt. о

где

С(ж,М1)

^^^^^^^™

^^^^^^^™

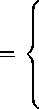
sin У—Ai t sin У—Ai (1

^^^^^^^™

ж)

^^^^^^^™

Ai sin

^^^^^^^™

Ai

sin V—Ai ж в™ V—^1(1 — 1)

^^^^^^^™

Ai sin

^^^^^^^™

Ai

0 < t < ж, ж < 1 < 1

— функция Грина. Возвращаясь к функции т(ж), равенство (14) перепишем в виде

1 т(ж) У о

G^x, t, Ai)y(l) dt + /(ж),

где

/ =

1 ад - у о

G(x, t, Ai){2 + Ai/t(l)} dt.

Из равенства (11) имеем

, X , X , (Х\    , /ж + 1\     / XX (х — 1А г/(ж,0) = т(ж) = 'фг (-) + Д2 (^^—J -ш V^J ” ш (-2/ ’       ^16^

, X , X 1 , , (X \     1 ,, /ж + 1А 1 , / ж \     1 , /ж — 1 А .

м_у(ж,0) = ж(ж) = --^_г    + -'Ф₂ —— - -ш - -ш  —— .    (17)

Подставляя (16), (17) в равенство (15), получим интегро-функциональное уравнение

Ш("9 +Ш (^"1) = I /^^^^^{^("f) +Ш'(| "I)} dt + 9^, (18) о где

д(ж) = [ С(жД,А1)               + |)| ^ + ^1(|) +^(^^) +/(ж).

о

Дифференцируя равенство (18), получим ш' (“ 2) “ ш' ^2 ~ 2) = ,/ ^Ж(ж’^ ^ {ш'(”2) + ^'(2 ” 2) } ^ = -29'^ж^ (19) о

Обозначая ш' (— |) = p(z), получим интегро-функциональное уравнение вида

р(г) - р ^-z - - ^ = - I £Дж, у, Ai) ^p(t) + ^(”^”2)} ^ ~ 2g(-2z).

о

Функцию p(z) будем искать в виде p(z) = r(z) — r^—z — ^.

Учитывая последнее слагаемое в равенстве (20), получим функциональное нение

урав-

r^-T^-z- |) = -2д^-2г^

которое является частным случаем линейного функционального уравнения [4]

AfWWHBfM^=F^,

где t — переменная, А, В, ■г/Д), ?(t), F(t) — заданные функции t, f — неизвестная операция, обращающая уравнение (22) в тождество.

Используя теорию итерационного исчисления, доказывается, что функциональное уравнение (21) имеет решение [4]. Из единственности решения задачи 1 следует, что функция ш(у) определяется единственным образом. Таким образом, функция и(ж,у) полностью определена в области Q.

Пусть теперь Аг — 0, A3 > 0. Доказательство единственности решения задачи 1 в этом случае проводится аналогично предыдущему.

В области Иг общее решение уравнения (1) имеет вид (3), где Дж, у) — общее решение уравнения

V_Xx — ^уу + А₃/У = 0-                                (23)

Решение задачи Коши с начальными данными

^(ж,0) = и(ж,0) = т(ж), му(ж,0) = иу(ж,0) = «(ж), имеет вид [5]

ж+у

^,_s)-^4±i!^₊i у MV^VE^^htods

+ Н T^^J«('A'=A^<>^)«Ю^„ ж-у где Jq (^) — функция Бесселя первого рода нулевого порядка. Удовлетворяя (24) краевым условиям (2'), получим

Ж

т(ж) = 2^ (|) - 2^(0) + j J_o ^V^aV^^ - $YH^ dE о

ж

+ 9 [ ^T^-^-Jo(V^3V^^ - ^ж)) ^ - 2ш (-9) , Z J          U JL-                                                \      /

о

Ж

т(ж) = 2^2 (^^) -2^2(0) - У Jo(\A3 V(€ - 1)(€ - ж))у(ж) J€

ж

+ У ^T^"g^Jo^V^3V^ -!)(€“ ^ж)) ^ - 2ш (---—^ .

После обращения интегральных уравнений (25), (26) относительно т(ж), соответственно получим [3]

Ж

т(ж) = 2^1 (|) -2ш(-|) + j J₀(VMx - ЕУМ^Ш о

ж

~"У ^° (^^"^ ж(ж ” ^) (^(2) ^(f)) ^ о

Ж

т(ж) =2^2 (^У“) - ^2ш (^) ~ / ^J° VVM-k + £М£)) dE

ж

“2 / -^-Jo(\A3V(1 “ ^ж)(^ “ ^ж)) Сфг^у;—) ^-ш(^—^-

J Ju                                                \ X Дд /          х Zi / 1

Равенства (27), (28) соответственно перепишем в виде

т(ж) =

Ж

У v(^)Jo(\A3(® -^)) dE о

ж

ж

+ У V’i ^|) Jo (V^sV^ж(^ж - €)) + I^ш' ^^-|) ^° (V^sV^t^^lT) dE-

о

о

т(ж) =

Ж

™У ^y(£Vo (V^a^ — ^ж)) dE

+

У < (^) ^о(^У(1-ж)(е-ж)) dE

ж

+ j ^ш' ^^—^ Jo (V^sV(1 ^{_ ж})(€ ^{_ ж})) dE- 1

В левую часть равенства (15) вместо т(ж) подставим (29) и полученное равенство продифференцируем по ж. В результате будем иметь смешанное интегральное урав нение где

Ж

у(ж) + [ v^-^-Jo

J ОХ о

(\Аз(ж - С)) ^d^ = j о

СДх^ХхММ

X

~ ^Ш' ( 2) ” j ^Ш' ( I) дж^^^^^Ж(^Ж “ €)) + 9'(^Ж): О

д(ж) = /(ж)

X

-1Фг ^|) ^о (V-^V^C^^IT) ^dJ- о

Если обозначить через R^x,^ резольвенту уравнения (31) и предварительно считать его правую часть известной, то решение этого уравнения можно представить по формуле

у(ж) —

j <Мх,СН^ d^ = -ш' (^) - У Q^x.^w' (-|) ^ + 9(ж) = р(ж),(32)

оо

<Мх^

<№^

= С_ж(ж,фА₁) + У Rlx^G^t^XiW. о

—   3^ (V^V х^х — С^ + Щх,^) + R^x^^tx-Jq^Vx^V ф(ф — О) dU,,

Ju                                                      J                kJ

х

9^ = У R(x,^q'^ dU о

Таким образом, получим относительно у (ж) уравнение Фредгольма второго рода. С помощью резольвенты Т^х,^ уравнения (32), значение у(ж) записывается следующим образом

1 у(ж)=р(ж) + У T^x^^pV^d^. о

Подставив значение р(ж) в равенство (33), получим

у(ж) = У М^х.^ш' (-|) d^ - ш' (-|) + Р(ж), о

где

(Мх^-Т^ + jT(x,^)Q^i,Mi, 0 < С <  х,

М^ =

-Т(_Ж,е) + jTlx^CM^M,, 5

х <е < 1,

Р^ = У Т(х,^<Ш о

С другой стороны, задачу (1), (2) в параболической части Qi области Q, и = еХ1У, можно свести к задаче заменой

vw=Vxx, ^(,0,у^ = e^^ip^yY п<Д,у^ = е^узДуУ

Решение задачи (35) имеет вид

^(®,у) = У о

т^С^Лх,уШ + У о

eXlhipi^G^0, h\ х, у^ dh

у

У eXlh(p2(h)G^l,h;x,y) dh, о где G^, h; х,у^ — функция Грина первой краевой однородной задачи (35). Найдем производную Иу, затем в полученном равенстве положим у = 0. Будем иметь

Эи "^w = а?

= [ W^M^ d^ + 0(ж), у=о {

где                         _        _

КМ = А1(<Ж0;ж,0) + Сж(С0;ж,0)), а е^ = — ех^у Эу

у

У e^Xlh

и j eXlh(p2(h)G^l,h;x,y) dh о

Подставляя теперь (15) в равенство (36), получим

у(ж) = У о

/*ч/

К(,х,^и^ d^ + 0(ж),

где

К^х,^ = У о

K^,^G^,^,X^d^

Обозначим через _А(ж,£) резольвенту уравнения (37), решение этого уравнения мы можем представить по формуле

«(ж)

= 0(ж) + j о

W^WM-

Подставляя выражение (38) для «(ж) в формулу (34) получим относительно ш' интегральное уравнение Фредгольма второго рода

Н)

^ш' ("I) ⁼ / ^M^V (-() d^ + e^, о

где 0(ж) = Р^ — «(ж).

Так как эквивалентность всюду сохраняется, то из единственности решения задачи 1 следует однозначная разрешимость интегрального уравнения (39).

Аналогичным образом можно получить интегральное уравнение (39) относитель-

—

I™

но ш' ^^^У Таким образом, определены функции т(ж), «(ж), ш(у). Следовательно, определена функция и(ж,у) в области Q. >