Краевая задача для вырождающегося уравнения третьего порядка

Фундаментальные результаты для вырождающихся уравнений второго рода эллиптического типа были получены академиком М.В. Келдышем [1].

При изучении так называемого стационарного вязкого трансзвукового линейного уравнения (или ВТ-уравнение)

u xxx ( x , У ) ⁺ u yy ⁺ yuy = f ( x , У ) .

Для случая a = 0, в работе [2], методом построения функции Грина в прямоугольной области, решена краевая задача. Также в работах [3, 4] в явном виде построены функции Грина некоторых внешних краевых задач в случаях: a = 0 и a = 1. Случай произвольного а исследован в [5]. Для вырождающегося модельного уравнения высокого нечетного порядка, краевая задача в прямоугольной области рассмотрена в работе [6].

Статья содержит две части. Первая часть содержит постановку задачи и доказательство единственности решения. Во второй части строится решение в виде бесконечного ряда по собственным функциям и доказывается её равномерная сходимость и возможность почленного дифференцирования по переменным x до третьего и по переменной у до второго порядков.

Постановка и единственность решения задачи

Для уравнения

L [ u ] = u xxx ^{+ а} 1 ( ^x ) u x ^{+ а} 0 ( ^x ) u ^- y m u yy = ⁰ ,                         ⁽¹⁾

где 0 <  m <  1, а 1 ( x ) e C ¹ [ 0,1 ] , а ₀ ( x ) e C [ 0,1 ] , рассмотрим следующую задачу.

Задача A . Найти в области ^ = { ( x , y ) :0 <  x , y <  1 } решение уравнения (1) из класса Cx’² ( Q ) п С² _у ( Q ), удовлетворяющее следующим краевым условиям:

u ( x ,0) = 0, u ( x ,1) = 0, 0 <  x <  1;

u (0, y) = Ф1( y), u (1, y) = Ф2( y), Ux (1, y) = Фз( у ), 0 < y < 1, где

^ ■( y ) e C ⁴ ( 0,1 ] ,   _{V l} (1) = ^ f(1) = 0,

Ф^ j ) ⁽ y ) = O

( 7

—m - j y 2

при y ^+ 0, i = 1,2,3, j = 0,4.

Теорема единственности . Если 2 a 1 x

(x) - a0 (x) < 0, то однородная краевая задача для урав нения (1) имеет только тривиальное решение.

Доказательство. Пусть u (x, у) - нетривиальное решение однородной задачи A. Рассмот рим тождество uL[и] = 0, (x,у)е Q .

Так как uuxxx

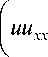
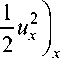
, ^и ( a l u x

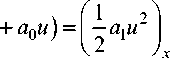
⁺ I a 0

-

2 a l x

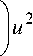
m y^muu_yy

( m ymuu

V

my

m - 1 2 A и

V у

^m ( 1 ^- m ) y m ² u ² m 2

-------Э-- y u y

то, подставляя их в тождество (2), а затем, проинтегрировав по области Q , получим:

1 1                  11             (

- J u x ( ⁰ , у ) dy ⁺ JJ ^{и 2} ( ^x , у ) I a 0

² 0               0 0           ^V

, , 1 , Л       ¹¹ ( m (1 - m ) _m_₉ 2

( ^x )^-T a 1 x ( ^x ) I ^dxd У ⁺П --- ~—-у ² u ²

^{2 V} 00 V ²

' m u 2

dxdy = 0,

отсюда получаем, что и (x, у) = 0.

Здесь учли, что из и ( x , у ) е C x’^ ( Q ) и и ( x ,0 ) = 0 следует и ( x , у ) = O ( у ) , при у ^+ 0. Теорема доказана.

Построение решения поставленной задачи.

Будем искать решение методом разделения переменных: и (x, у) = X (x )Y (у), тогда из уравнения (1) следует, что

X " + a (x) X ‘ + a 0 (x) X ymY" --------------------=----= -л, л > и

XY

Учитывая граничные условия относительно переменной у, получим следующую краевую задачу на нахождения собственной функции и собственного значения: ' Y '(у) + Лу - mY (у) = 0,

1 Y ⁽⁰⁾ = °,

Y (1) = 0.

Уравнению (3) удовлетворяют следующие функции [7]:

Y 1 ( у ) = J 1

2 - m

(2 л m)

2 - m^y

V           V

Y2 ( у ) = ^J- 1

2 - m

1 ² 2 Л "f m I

2 - my

V           V

где Ja (в) — функция Бесселя первого рода. Так как при 0 < m < 1 число —— не является це-2-m лым, то функции Y1 (у), Y2 (у) линейно независимы [8]. Поэтому общее решение уравнения (3)

имеет вид

Y ( у ) = д/ у

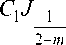
( 2 V I ²- m )

2 - m ^{у 2}

V           V

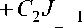
2 - m

( 2 Л 2- m ) 2^ m ^у

V           V

где С 1 , С ₂ - произвольные постоянные. Из представления функции Бесселя 1-го рода следует, что в окрестности у = 0 справедливы равенства

Y ( У ) = У ² J 1

2 - m

2 VI 27

y ²

2 - m

= O ( У ) , Y 2 ( У ) = У ² J -

2 - m V

2 VI 27

y ²

2 - m

= O (1).

Поэтому для удовлетворения краевого условия Y ( 0 ) = 0 мы должны положить C ₂ = 0, отсюда из условия Y ( 1 ) = 0, получим

Y (1) = J 1

Г 2 VII

2-m V

2 - m

= 0.

В силу —-— > 0 уравнение (4) имеет бесконечно много вещественных корней, причем все они 2-m простые [8]. Обозначим их через, un, где n = 0,1,2, Известно [9], что причем 0 < u0 < ж < и 2 <... < ж <....

...,

3 п п 1

ж »--1-----+ пп , n Е N .

n 4 2 2 - m

²V ^In             a I 2 - m _ _ I 2\ _c .

Тогда ж = ™— , отсюда I = ---- ж = O n , собственные функции имеют вид ^п 2 - m n V 2 ^{n !}

п        2- m Л

²V ¹ Ж7

у ²

2 - m

, n Е N .

^Yn ⁽ У ) = V yJ 1 2 - m V Если в качестве собственных функций взять

Y k ( У ) =

yJ ₁

2 - m

k y 2

2 - m

7!Jjl

2 - m V

k y2

2 - m

,

⁷ L 2

то система {Yk}k==+” будет ортонормированной. Поэтому в дальнейшем так и будем считать. Соб- ственные функции удовлетворяют также следующему интегральному уравнению:

Yt (У ) = Ik J G (У ,?? "Yk (?) d?,

где

G ( У Ж

I y (1 - ? ), У < ? <  1.

Действительно, имеем

y

y

Ik JG (y ,?)?~ mYk (?) d? = -JG (У Ж '«) d? = -(1 - У) J9k'(?) d? - У J (1 - Ж "(?) d? =

(                    y II                           1 I

= (1 - У) -?Yk(?),+ J Yk'(?) d? - У (1 - ?) Yk(?) у - J Yk?) d? =

V              0          7 V                  У 7

= (1 - У )(- УY‘ (У) + Yk (У)) - У (-(1 - У) Y (У) - Yk (У)) = - У (1 - У) Y‘ (У) + (1 - У) Yk (У) + +У (1 - У) Yk (У) + yYk (У) = Yk (У)- yYk (У) + yYk (у ) = Yk (у ).

Чтобы показать разложимость граничных функций ф _i ( y ) , i = 1,2,3 при некоторых условиях, по системе собственных функций { Y k } k =+ , воспользуемся теоремой Гильберта-Шмидта. Для этого предварительно превратим полученное интегральное уравнение в уравнение с симметричным

m ядром. Это делается обычным способом, т.е. умножением обоих сторон уравнения (5) на y 2

Тогда имеем m1mmm

У ² Y ( У ) = A -j У ² G ( У , 4 ) 4 ² Y k ( 44 ² d 4 .

Введем обозначения

m    mm	, m 4 2	^ m 1 m у 2 - у 2
f k ( у ) = у 2 Yk ( у ) , F ( у , 4 ) = у 2 G ( у , 4 ) 4 2 = •	m	У              7 2 m 1 m ^
	у 2	4 -4 2
	1	У            7

Отсюда получим интегральное уравнение с непрерывным , по обоим переменным , и симметрич -

0 ^ 4 ^ y, y ^ 4 ^ 1.

ным ядром

fk (У) = Ak JF(У,4) fk (?)d4.

m

Тогда функция y ² ф _i ( y ) , где ф _i ( y ) , i = 1,2,3 граничные функции, выражается

через ядро

F ( y , 4 ) следующим образом:

в самом деле,

2 -

m

m

m

y 2ф(y) = JF(y,4) -42Ф^4 d4,

1 m 2 1 - m

- Jf (y ,4)42 ф'(4) d4 = y 2

-

1 -

y

1 -

m

- y

m

m V -           1 - m '

2 J4d^(4)-y 2 J(1 -4)d^(4) =

-           1 1 - m

-Ф‘(y)-JФ^4)d4 -y 2

1 -

m

m

-

m

-

m

y

(1- у M( y)+J^(4) d4 =

2 -

m

1 -

m

m

= y 2 Ф (y)-y 2 Ф^ (y)-y 2 Фi( y ) + y 2 Фi( y ) + y 2 ^i (y)-y 2 ^i (y ) + y 2 Фi( y ) = y 2 Фi (y).

mm

Так как функции y 2 pt (y), 42 Ф’(4) непрерывны на отрезке [0,1], то по теореме Гильберта- m

Шмидта функция у ² ф _i ( у ) разлагается в регулярно сходящийся ряд по собственным функциям

m у 2 Yk (у) ядра F(у,4), т.е.

m ^ m у 2 ф(у) = Еck- 2 Yk (у), k=1

где

ck = Jy-тф(у) Yk (у) dy .

m

Разделив на y ² , окончательно получим

^

Ф ( у ) = Е ^ck^Yk ( у ) .

k = 1

Относительно переменной x получим краевую задачу

Xk +vkXk = (ai (x) Xk + a о (x) Xk) _ Xk (0) = ^ k, Xk (1) = ^2 k, Xk (1) = ^ k, где

1                                                                                      I 2 1

V ik = J ^ i ⁽ y^{) Y}k ⁽ y ) y m dy , i = ¹ , ^{2,3, v} k ³ = ^ k , ^v k = O ^{k 3} .

0                       kJ

Обнулим краевые условия в задаче (6), для этого введем новую функцию Z (x) по формуле: Z ( x ) = X ( x )-x ( x - 1)^3 k - x ( 2 - x )^2 k -( x - 1)2 V1 k, тогда получим краевую задачу в виде

| Zk + vk Zk = f (x)- (a1 (x) Zk + a о (x) Zk),

\ Z k (0) = Z k (1) = Z k (1) = 0,

где f (x )= (vk + a 0

13k + x ( 2 - x)V2k +(x - 1)2 Ф1 k )--a1 ( x )(( 2 x - 1)^3 k +( 2 - 2 x ) ^2 k + ( 2 x - 2)^1 k ).

Сведем задачу (7) к интегральному уравнению, которую в дальнейшем решим методом последовательных приближений. Функция Грина G_k ( x , £ ) задачи (7) имеет вид [2]:

где

Gk (x,^) = A

^-v k

- 2 e

+ 4 e ²

Gk (x,£) = A

^-v k

2 e

v 3 n

V +

2 ^k 6

n

- 2 e ²

+ 2 e ²

3„            V31Z sin T vk(1 - ^) sinT vkx,

- 2 e ²

+ e ■ ■ ^{( x -}^ + 4 e 2

■ V 3 n Tt ^sin -r^vk§ ⁺T 2       6

- 2 e

sin — v ( 1 - x ) + ^П sin 2 ^{kV !} 6

к

A = 3v2

1 - 2 e -

Из представлений (8),(9) и (10) имеем

а для производных сп d s G k ( x ,Q d t^s

IGk (x,O|< M0,M0 > 0 vk раведливы соотношения

2. /3         1

sin _T ^V k ^ ⁺

k            J

. V3 ,, x n

sin T vk ($- x)+-+

0 < x < ^,

. V3., , n sin —V +— k 2 k 6 JJ

3n \ n

—V (1 -x) + — +

2 ^{k (} ) 6

П И

6 Jj

.

– некоторое число,

£ < x < 1,

V k 2 , ⁵ = 1,2,3,4, M s >  0 - некоторые числа, t = x , либо t = ^

Задача (6) эквивалентна интегральному уравнению вида:

Zk (x ) = J f (£) Gk (x ,^) d^ - J (ai (£) Zk(^) + a о (£) Zk (^)) Gk (x ,£) d^ =

где

= F ( x ) + J I — ( a_x ( f ) G k ( x , f ) ) - a о ( f ) G k ( x , f ) I Z_k ( f ) d f , о V ^df                                )

F ( x ) = J f ( f ) G k ( x , f ) d f .

о

Будем решать полученное уравнение методом последовательных приближений

Z k ⁰ ( x ) = F ( x ) , Z ‘ ^{+ 1} = F ( x ) + J I — ( a_x ( f ) G k ( x , f ) ) - a о ( f ) G k ( x , f ) I Z k ( f ) d f , о ^{V df}                                       '

Если учесть ограниченность функций a0(x), a1 (x), a( (x), оценки для функции Грина, то начиная с некоторого номера k , будем иметь

\ Z k ⁺¹| <  K1 F ( x ) ¹ +

d G k ( x , f ) d f

d G_t ( x , f ) ² d f

+ ... +

d G ( x , f ) d f

отсюда

|Zk (x)|< K1 F(x)|

d G k ( x , f ) d f

< M о F ( x )| <  N о ( ^ 1 k I ⁺ | k k | ⁺ | k k I) ,

где K 1 , M о , N о - некоторая положительная постоянная.

Аналогично можно показать выполнение следующих неравенств:

Z k '( ^x ) <  M 1^Vk\^F ( ^x )| , Z k 4 ^x ) <  M 2 ^ 2 I F ( ^x )| ,

Zk" (x) < M3Vk IF(x)| = M3^k IF (x)| < NЛ (^1 k | + |kk | + |kk I), где M1, M2, M3, N3 - некоторые положительные постоянные, не зависящие от номера k . Формальным решением поставленной задачи будет ряд ^

u ( ^x , y ) = Е Y k ( y ) X k ( ^x ) .                                 ⁽¹¹⁾

k = 1

Чтобы этот ряд был классическим решением поставленной задачи А, нужно показать возможность почленного дифференцирования ряда (11) по переменной x до третьего и по переменной у до второго порядков (именно эти порядки входят в уравнение). Из вышеуказанного имеем

^

Iu (x, у )|< M Е Yk(у )| (k^ k|+ |^2 k| + ^3 k |) , k=о где M - некоторая положительная постоянная.

Покажем сходимость рядов участвующих в правой части этого неравенства. Применяя неравенство Коши-Буняковского, получим

ЕЕ Y k ( у ) k 1 . 1= ЕЕ Y k j y ) ^ k k i s. ЕЕ f ’ ‘ Е ^{у )} 1\ /Еёшо² , - = 1,2,3.       (12)

k = о               k = о ^A k            V k = о V ^A k J V k = о

Покажем теперь сходимость каждого ряда в неравенстве (12). Имеем kk = J У - mk.( У )’к (У) dy = о

-^Jk(У)Yk(У)dy, kе N,i = 1,2,3, Хк о отсюда

^kkik = J (-kf( У) ym) У - mYk (У) dy, k е N, i = 1,2,3 , о применим здесь неравенство Бесселя

+^

= J (фГ ( y ) ) y m dy , i = ¹ , ^2,3, 0

X (^ik^k) < ф.'(y)y k=0

интеграл в неравенстве (13) существует и, значит, ряд сходится.

Теперь вернемся к задаче (3), которая эквивалентна интегральному уравнению

Yk (y) = Лк JG(y,??mY (?)d?, отсюда

Yy = J G ( y , ?? ” Y_t ( ? ) d ? , k 0

по неравенству Бесселя, имеем

X Y k y y ) j <  J G ²( y , ?? m d ? .

k = 0 к ^X k ) 0

оценим последний интеграл:

1 y 1

JG2(y,??md? = ?m(1 -y)2d? + Jy2(1 -?)2?md? <—— + 2I-1- +    + -^j = N.

3 - m 11 - m 2 - m 3 - mJ

00 y

( Y ( y )

Следовательно, ряд ^k сходится и равномерно ограничен. Покажем теперь равномер- k = o к ^X k )

ную сходимость ряда (11)

n+p n+p

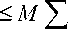
Y k ( y ) X k

X k ( ^ф 1 k\ ^{+ ф} 2 k\ ^{+ ф} з k |) <

X Yk (y) Xk (х)

k=n nX' r Yk(y) k=n к Xk

In + p г n + p г n + p 7 X ( X k Ф, k I) ² +< X ( X k Ф 2 k I) ² +< X ( X k ф з k I) ² k = n v k = n \ k = n

<

^ n + p           Г I n + p           Г n + p           "7 ^л

< MN < X (Xk фРхk\Y +x X (Xk Ф2k I)2 +A X (Xk фзk I)2 .

k = n                  V k = n

Учитывая (13) имеем, что для любого p > 0 суммы, стоящие в правой части, стремятся к нулю при n ^+^ . Принимая во внимание, что правая часть не зависит от переменных (х, y), мы можем утверждать, что ряд (11) сходится равномерно в квадрате [0,1] х [0,1].

Аналогично доказывается возможность почленного дифференцирования бесконечного ряда (11) по переменным x до третьего и по y до второго порядка (т.к. в исходное уравнение входят частные производные этих порядков).