Целью настоящей работы является показать, каким образом синтезировать на заданном базисе функцию распределения поля на излучающей апертуре, обеспечивающую создание заданного (требуемого) поля излучения. При этом указанный базис определяется геометрией излучателя, пространством функций задачи, описывающей этот излучатель как базовый элемент общей структуры. В рассматриваемом случае излучающей апертурой является торец открытого диэлектрического волновода (ОДВ). В связи с этим в качестве пространства базисных функций, описывающих первичное поле, берутся решения краевой задачи для регулярного ОДВ.

Строгость или не строгость данного подхода к расчету поля излучения зависят от того, каким образом определяется распределение электромагнитного поля на раскрыве излучателя. В большинстве случаев для этого используются методы геометрической оптики, когда не учитываются дифракционные явления на краях и внешних поверхностях раскрыва и обратное влияние поля излучения на распределение поля первичных источников. Более строгий анализ и экспериментальная проверка показывают, что приближенность определения первичного поля приводит к заметным ошибкам в расчете поля излучения в области боковых и задних лепестков диаграммы направленности.

Строгая теория антенн приводит [1; 2] к интегральным уравнениям. При этом, как правило, поднимается вопрос самосогласованности задачи об излучении. Под самосогласованностью в большинстве случаев [2–5] понимают сведение задачи к неоднородному сингулярному интегральному уравнению относительно функции тока на апертуре антенны, учитывающей влияние внешнего поля на распределение этого тока. При этом в записи первичного поля учитывается ЭДС сторонних сил [2], что приводит к неоднородному интегральному уравнению (системе уравнений), что, вообще говоря, нарушает смысл самосо-гласованности задачи, так как в конечном итоге приводит к расчету поля излучения по заданным источникам. Самосогласованность в этом случае, как таковая, отсутствует. В строгом представлении самосогласованная задача – замкнутый цикл, содержащий обратную связь наподобие системы автогенератора. В результате наличия указанной обратной связи самосогласованная задача об излучении должна приводить к однородным интегральным уравнениям, то есть

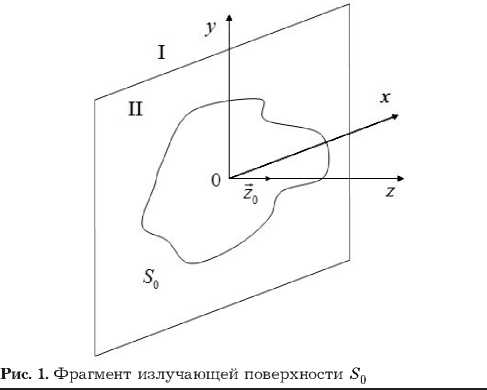
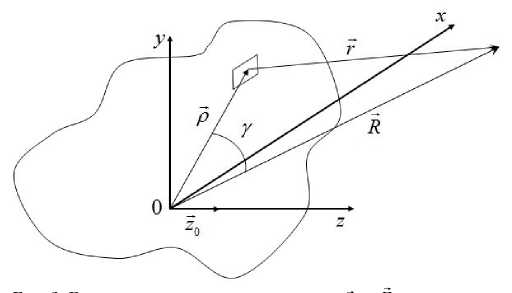
Рис. 2. Взаимное расположение векторов р и R , определяющих, соответственно, положение элементарного тока на поверхности S ₀ и точку наблюдения

j e = [ z o , н ] , 1 m = -[ z o , E i ] .                    (1)

должна являться задачей на собственные функции и собственные значения. Последние являются решениями характеристического уравнения. Только на решениях этого уравнения получаются [6; 7] нетривиальные решения краевой задачи об излучении.

Самосогласованность задачи можно трактовать как ее «самодостаточность» – независимость от первичных источников. Это говорит о том, что сама по себе самосогласованная задача не позволяет производить расчет характеристик излучателей, а является лишь основой организации этой процедуры. Подобно закрытым электродинамическим структурам она позволяет определить базис задачи о возбуждении поля в открытом пространстве и на основе этого базиса распределение токов (полей), обеспечивающее заданные характеристики поля излучения.

Предлагаемая трактовка является попыткой уточнить терминологию, объяснить смысл понятия самосогласованности. Показывается, что самосогласованная задача в теории излучения приводит к однородным интегральным уравнениям Фредгольма 2-го рода, то есть является задачей на собственные функции и собственные значения.

1. Формулировка самосогласованной задачи об излучении

Излучающий торец ОДВ, включающий в себя внутреннюю и внешнюю области, представляем как плоскость S ₀, по которой протекают элек- 1 e трические и магнитные токи с плотностями j и j m , соответственно (рис. 1).

Согласно принципу Гюйгенса – Френеля [8] плотности поверхностных токов на S ₀ связаны с полями соотношениями:

Произвольные токи, распределенные в конечном объеме V, в области II (z > 0) создают поле, описываемое векторными потенциалами:

a e =±  1 e e—dV ,

4 п        r

V

A m = -- 1 m — dV ,

4 n         r

V

где r — радиус-вектор, соединяющий элементарный ток на поверхности S ₀ с точкой наблюдения; R — радиус-вектор точки наблюдения (рис. 2). Модули векторов 1 и R связаны соотношением:

r = р ² + R ² - 2 р R cos у , где р — модуль радиус-вектора р элементарного тока на поверхности S o ; Y — угол между векторами р и R (рис. 2).

Выражения (2) соответствуют общему случаю, когда, например, излучающая поверхность имеет конечную по z толщину. При бесконечно тонкой поверхности, на которой выполняются граничные условия (1), в выражениях (2) выполняется поверхностное интегрирование, а 1 ^е = 1 e , 1 m = — m .

В однородной среде векторные потенциалы, создаваемые электрическими и магнитными токами, удовлетворяют волновым уравнениям:

д² 1 ^е

А А ^е -БЦ^- = -Ц j e ,                     (3)

d 11^

² 1 m

А A m -бц^-^ = б j m .                   (4)

д t

В том случае, когда поле излучения создается поверхностными токами, векторные потенциалы (2) вычисляются как

• - ikr

А ^е =-Ц[[ z о , H ]----- dS ,                    (5)

• 4 п             r

  ■ - ikr

  A m = -М|" ■ о, E 1---- dS .                  (6)

  4 n             r

  S ₀

  Тангенциальные компоненты полей в области

  II (рис. 1) вычисляются по формулам:

  
  

  E^ =

  
  

  - i to A e + — rotA m , Z o

  
  

  e

  
  
  
  

  H (ⁿ⁾ =

  
  

  i to A m

  
  

  1      ^— e —

  +— rotA , z о .

  Ц           _

  
  
  
  

  На излучающей поверхности S ₀ должны выполняться граничные условия:

  
  

  E_T|

  ^T S o

  —►

  
  

  EE!

  
  

  ^:T"l S o , ^H 4

  
  

  ' T

  
  

  Is = H — i^n||

  S ₀

  
  

  S 0 ,

  
  
  
  

  —*

  
  

  где E _т и H _T — это поля на поверхности S o , связанные с токами на этой поверхности соотношениями (1).

  Подставляя в граничные условия (9) компоненты поля (7) и (8) в области излучения II, получаем:

  
  

  —►

  E т

  
  

  4 n

  
  

  _-

  
  

  i toц J H т

  S 0

  
  

  - ik ^—

  ----dS +

  r

  
  

  <

  
  

  + rot

  
  

  —►

  H т

  
  

  + rot

  
  

  J E

  
  

  e - ikr

  
  

  r

  
  

  dS , — 0

  
  

  ^,

  
  
  
  

  4 n

  
  

  i toe J E.

  S 0

  
  

  ' T

  
  

  e

  
  

  ,- ik ^—

  ^:----dS +

  r

  
  

  J ^H H

  V S о

  
  

  —► e - ikr

  
  

  A

  
  

  r

  
  

  dS , Z o

  
  

  .

  
  

  Уравнения (10)

  
  
  
  

  образуют систему

  
  

  двух век-

  
  

  торных интегральных уравнений относительно

  
  

  В самосогласованной задаче поле на излучающей поверхности полагается неизвестным. Оно ищется как решение интегрального уравнения или системы интегральных уравнений (10). Поскольку задача на собственные функции и собственные значения приводит к характеристическому уравнению, она имеет множество решений, образующее базис для представления поля, создаваемого заданным источником. Этот базис, полученный как решение самосогласованной задачи, учитывает обратное влияние поля излучения на первичный источник. Решение самосогласованной задачи, естественно, удовлетворяют уравнениям Максвелла, поскольку поля, входящие в ее формулировку, вычисляются через векторные потенциалы, удовлетворяющие уравнениям (3) и (4).

  2. Самосогласованная задача об излучении с конца круглого открытого диэлектрического волновода

  Одной из широко распространенных электродинамических задач является задача об излучении с конца круглого открытого диэлектрического волновода. Базовым фрагментом такой задачи является задача об излучении с круглой области диэлектрической поверхности.

  В соответствии с формулировкой самосогласованной задачи об излучении, базис для представления поля над круглым фрагментом диэлектрической поверхности (торцом ДВ в неограниченном однородном пространстве (рис. 3)), будем формировать на основе решения однородной краевой задачи, сводящейся к системе однородных интегральных уравнений Фредгольма 2-го рода (10).

  
  

  тангенциальных компонент электрического и магнитного полей на излучающей поверхности S ₀. Как видно из (10), интегральные уравнения однородные. Таким образом, имеем задачу на собственные функции и собственные значения. Такая задача, сформулированная в виде замкнутого цикла (поле излучения вычисляется через неизвестное поле на поверхности излучения и подставляется в граничные условия на этой поверхности), называется самосогласованной. В ней отсутствует заданное стороннее поле. Задачи, в которых это поле присутствует, приводят к неоднородным интегральным уравнениям. Такие задачи не следует классифицировать как

  
  
  

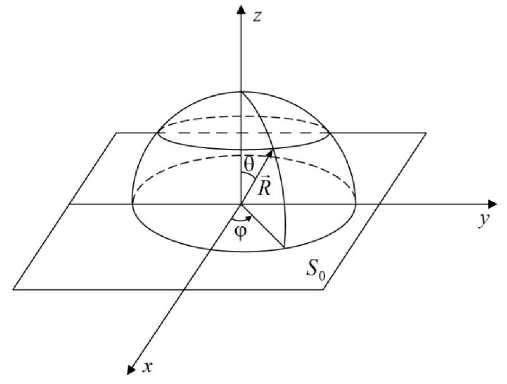
  Рис. 3. Связь декартовых и сферических координат, определяющих положение точек пространства над торцом ДВ

  
  

  самосогласованные.

  
  

  При круговой апертуре (круглое отверстие в проводящем экране, торец круглого ОДВ) система интегральных уравнений (10) в компонентной записи, соответствующей рис. 2, при-

  
  

  ливается на основе интегральных уравнений, в конечном счете получаемых из уравнений Максвелла. В этом случае самосогласованная задача решается спектральным методом, и ее собствен-

  
  

  водится к виду:

  
  

  2 п ю

  
  

  E Р =

  
  

  —

  
  

  5/J H ф

  
  

  e

  
  

  ,^— ikr o

  
  

  <

  
  
  
  

  г

  r_o

  
  

  p ■ d p ■ d ф o ,

  
  

  2 п ю

  
  

  H ф =

  
  

  _—

  
  

  i sr /z E p

  
  

  e

  
  

  ,^— ikr o

  
  
  
  
  
  

  г

  r_o

  
  

  р ■ d р ■ d ф o .

  
  

  2 п ю

  
  

  E ф = 5// H »

  
  

  e

  
  

  ,^{— ikr}o

  
  

  <

  
  
  
  

  r_o

  
  

  р ■ d р ■ d ф о ,

  
  

  2 п ю

  
  

  H р = 5/J E ф

  
  

  e

  
  

  .^— ikr o

  
  
  
  
  
  

  r_o

  
  

  р ■ d р ■ d ф о ,

  
  

  где r_o определяется по формуле

  Г о = V R ² + р ² — ² р R cos ( ф —ф о ) ;

  p определяет положение точки со сферическими координатами ( р , 9 _о , ф _о ) . Отметим, что система (11) может быть получена из системы (12) (и наоборот) с помощью перестановочного принципа двойственности [3], что подтверждает корректность их (систем) вывода.

  Можно сформулировать два подхода к расчету поля излучения на основе уравнений (11) и (12). Первый подход предполагает автономность систем уравнений (11) и (12), как получаемых одна из другой с помощью перестановочного принципа двойственности. При этом любая пара компонент: E p , H ф или E ф , H p находится, соответственно, из уравнений (11) или (12), другая определяется согласно принципу двойственно-

  
  

  ные значения находятся как совместные решения двух характеристических уравнений, получаемых в результате алгебраизации двух систем интегральных уравнений.

  На основе сформулированной самосогласованной задачи об излучении, приводящей к системе однородных интегральных уравнений Фредгольма второго рода (11), (12), можно поставить задачу синтеза функции источника, создающего заданное поле излучения. В этом случае в интегральных уравнениях (11), (12) свободные функции полагаются заданными, а искомые функции источника, создающего заданное поле, входят под знак интеграла. В результате от системы однородных интегральных уравнений Фредгольма 2-го рода переходим к системе неоднородных интегральных уравнений Фредгольма 1-го рода. При этом исходная самосогласованность краевой задачи позволяет учитывать обратное влияние поля излучения на источник. Базис для разложения синтезируемой функции источника выбирается на основе геометрии излучателя и,

  
  

  как правило, соответствует пространству его собственных волн.

  Рассмотрим случай реализации поля излуче-

  
  

  ния с торца круглого диэлектрического волно-

  
  

  вода, распределенного по гауссову закону:

  
  

  сти.

  Другой подход предполагает изначальную связанность систем (11) и (12), их совместное решение относительно всех четырех компонент. При этом, согласно спектральному методу [9], ком-

  
  

  поненты поля подвергаются автономным разложениям, коэффициенты которых определяются из совместного решения систем интегральных уравнений (11), (12).

  Таким образом, при первом подходе предполагается автономность систем интегральных уравнений и получение решений второй из них с использованием принципа двойственности из решений первой. При втором подходе системы уравнений (11), (12) решаются совместно в предположении независимости разложений компонент поля, связь между которыми устанав-

  
  

  E ( R , ф ) = Ae ^y( Ra ) cos ( n ф ) , ^р                      2                                (13)

  H ф ( R , ф ) = Be ^y( Ra ) sin ( n ф ) ,

  E ф ( R , ф ) = B J ee ~^Y( Ra ) sin ( n ф ) ,

  Г 2                      (14)

  H p ( R , ф ) = AJ~e ^Y( Ra ) cos ( n ф ) .

  В этом случае, подставляя в (11), (12) в правые части разложения полей по собственным волнам ОДВ с индексом n = 1, в левые части — выражения (13), (14), получаем:

  
  

  Ae ^y( Ria ) cos ( n ф ) =

  
  

  M    2 пю

  =— 5x A 1 m // H s m'

  m = 1      0 0

  Be ^y( Ra ) sin ( n ф ) =

  
  

  _e ^— ikr o

  p- d p- d ф о , r_o

  
  
  
  

  —

  
  

  M

  
  

  2 п ю

  
  

  i roe

  17 ^ A i m //

  m = 1      0 0

  
  

  ( m ) e

  E p -

  
  

  ,^{— ikr}o

  
  

  r_o

  
  

  Р" d p" d ф о ,

  
  
  

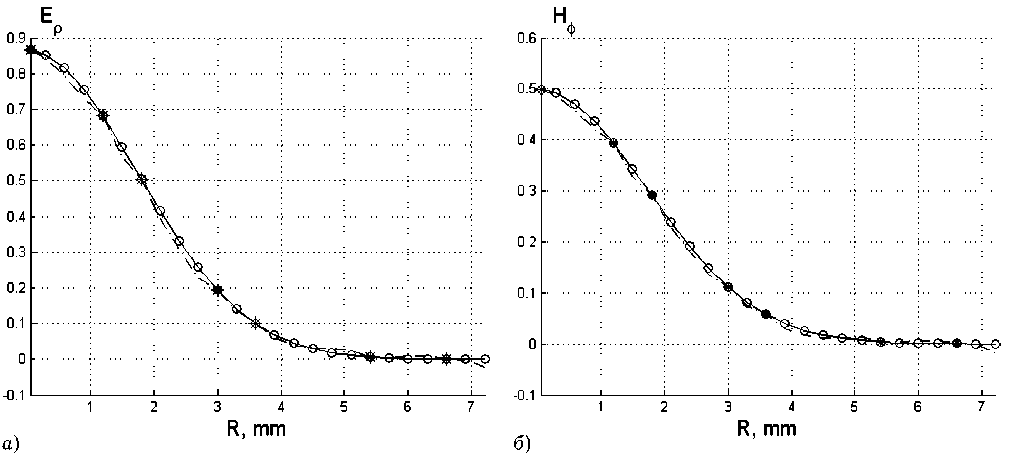
  Рис. 4. Сравнение сумм в правых частях системы (15) с заданным распределением (13) для случая семи узлов коллокации с радиальными координатами R ^ = 0.06 mm, R 2 = 1.2 mm, R 3 = 1.8 mm, R 4 = 3 mm, R 5 = 3.6 mm, R ₆ = 5.4 mm, R 7 = 6.6 mm и азимутальной координатой ф = 30 ° : а ) реальная составляющая правой части первого из уравнений (15); б ) реальная составляющая правой части второго из уравнений (15)

  
  

  B

  
  

  ¹ sin ( П ф ) =

  
  

  M    2 пю

  
  

  <

  
  

  = ^X A m II m = 1      0 0

  
  

  ( m ) e

  H р

  
  
  
  

  ikr_o

  ----р ■ d р ■ d ф o ,

  
  

  r_o

  
  

  A Еe ( Ra ^{) 2}

  \ Ц

  
  

  cos ( n ф )

  
  

  M

  
  

  2 п ю

  
  

  i roe

  = 4Л ^ A ¹ m ¹¹

  m = 1      0 0

  
  

  ( m ) e

  E ф

  
  

  _{_}

  
  

  ikr_o

  ----р ■ d р ■ d ф o .

  
  

  r_o

  
  
  
  

  В дальнейшем рассматриваем только систему (15). Поиск амплитудных коэффициентов A _{1 m} и сумм в правых частях системы (15) производим для следующих параметров: A = 1, B = 1 — амплитудные коэффициенты из выражений (13); a = 6 mm - радиус ОДВ; Y = 6 — коэффициент из выражений (13); n = 1 — азимутальный индекс волн ОДВ; ё 1 = 2.04, § 2 = 1 — относительные диэлектрические проницаемости внутренней и внешней областей, соответственно; ц 1 = ц 2 = 1 — относительные магнитные проницаемости; f = = 185 ГГц — частота, на которой производился

  
  

  расчет.

  Алгебраизация уравнений (15), (16) осуществляется методом коллокаций [10] с эквидистантной сеткой в плоскости ( R , ф ) . Выбор частоты 185 ГГц связан с тем, что при заданных параметрах диэлектрического волновода на данной частоте распространяется 15 волн с азимутальным индексом n = 1, что позволяет использовать достаточное для качественной аппроксимации

  
  

  количество узлов коллокации (вплоть до семи узлов).

  На рисунках рис. 4, а , б , рис. 5, а , б приводятся результаты суммирования членов ряда (штрих-пунктирные линии) в правых частях системы (15) для случая семи узлов коллокации. На этих же рисунках приводятся заданные распределения полей (13) (сплошные линии с круглым маркером). Мнимые части сумм рядов практически обращаются в нуль. Маркерами в виде звезды показаны значения в узлах коллокации.

  Приведенные численные результаты свидетельствуют о том, что система интегральных уравнений, к которой приводит самосогласованная задача об излучении в открытое пространство, позволяет находить функцию распределения токов первичных источников, создающих заданное поле излучения. Предлагаемый подход обеспечивает установление связи между задаваемыми характеристиками поля излучения и пространством собственных функций краевой задачи, соответствующей апертуре излучателя. Поскольку эта связь устанавливается в рамках самосогласованной задачи, в ней учитывается обратное влияние поля излучения на первичный источник.

  Если обычно в задачах о возбуждении алгоритм вычисления амплитуд спектральных составляющих основывается на ортогональности собственных функций соответствующей краевой задачи, то в предлагаемом подходе амплитуды спектральных составляющих, обеспечивающих

  
  
  

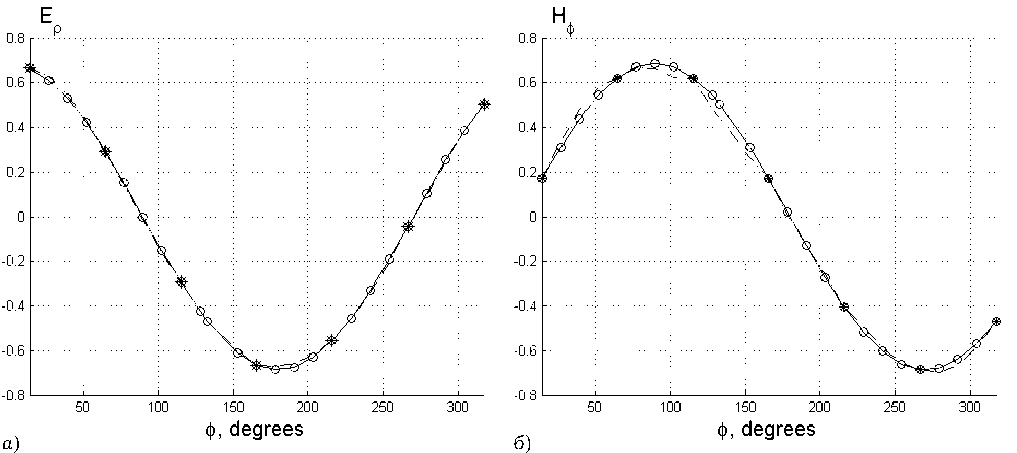
  Рис. 5. Сравнение сумм в правых частях системы (15) с заданным распределением (13) для случая семи узлов коллокации с азимутальными координатами ф 1 = 14.4 ° , ф 2 = 64.8 ° , ф з = 115.2 ° , Ф 4 = 165.6 ° , ф ₅ = 216 ° , ф 6 = 266.4 ° , Ф 7 = 316.8 ° и радиальной координатой R = 1.5 mm: а ) реальная составляющая правой части первого из уравнений (15); б ) реальная составляющая правой части второго из уравнений (15)

  
  

• 4.    Электродинамика и распространение радиоволн / В.А. Неганов [и др.]. М.: Радиотехника, 2007. 743 с.

• 5.    Неганов В.А., Павловская Э.А., Яровой Г.П. Излучение и дифракция электромагнитных волн. М.: Радио и связь, 2004. 263 с.

• 6.    Раевский А.С., Раевский С.Б. Самосогласованность краевых задач теории излучения // Антенны. 2014. Вып. 2 (201). С. 3–6.

• 7.    Самосогласованная задача об излучении из круглого отверстия в бесконечном идеально проводящем экране / Г.С. Малышев [и др.] // Антенны. 2015. Вып. 3 (214). С. 3–9.

• 8.    Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988. 440 с.

• 9.    Агалаков А.Н., Раевский С.Б., Титаренко А.А. // Журнал вычислительной математики и математической физики. 2013. Т. 53. № 7. С. 1113-1123.

• 10.    Алексидзе М.А. Фундаментальные функции в приближенных решениях граничных задач. М.: Наука, 1991. 352 с.

требуемое поле излучения, находятся из системы интегральных уравнений, то есть последняя позволяет синтезировать функцию источника под заданные характеристики поля излучения.

Заключение

Показано, что самосогласованная задача об излучении приводит к системе однородных интегральных уравнений, дающей базис для обоснованного решения задач возбуждения поля в открытом пространстве подобно задачам возбуждения полей в экранированных структурах. Самосогласованная задача, как показано на конкретном примере, позволяет синтезировать функции источника, создающего заданное поле, с использованием базиса, соответствующего краевой задаче для структуры, образующей апертуру излучения. Показано, что для численной реализации задачи синтезирования можно успешно использовать метод коллокаций.

Работа выполнена при поддержке Российского научного фонда (проект № 17-19-01628).