Криминологическое прогнозирование на основе тренда при недостаточном качестве описания исходных данных

Введение. Отмечается, что криминологическое прогнозирование на основе трендовой модели, обладая рядом бесспорных достоинств по сравнению с другими видами криминологического прогнозирования, имеет существенные недостатки – невозможность обеспечения заданной точности прогноза, а также ограниченные возможности прогнозирование в случае недостаточной точности описания наблюдаемых данных. В статье исследованы возможности улучшения качества описания данных при построении трендовых моделей.

Материалы и методы. Исследование основывается на справочных данных о состоянии преступности и методах математической статистики.

Результаты исследования. Предложен подход к криминологическому прогнозированию на основе тренда при недостаточном качестве описания исходных данных, основанный на изменении функциональной зависимости модели и снижении влияния аномальных данных Предложенный подход реализован для решения задачи краткосрочного прогнозирования количества зарегистрированных преступлений в республике Бурятия. Удалось на 25% улучшить качество описания данных и получить достаточно точную интервальную оценку прогноза.

Также показано, что интервальное прогнозирование предоставляет более полную и надежную информацию для принятия решений и оценки рисков, поэтому оно предпочтительнее точечной оценки прогноза.

Выводы и заключения. На основе проведенного исследования авторы считают возможным рекомендовать для улучшения качества описания данных трендовой модели:

– анализ качества описания данных при различных формах функциональной зависимости трендовой модели путем сравнения коэффициентов детерминации и оценки точности прогноза;

– проведение проверки наличия аномальных данных с последующим исключением их из рассмотрения или уменьшением их влияния за счет изменения интервала наблюдения.

• 5.1.4.    Criminal Law Sciences

(legal sciences)

Original article

TREND-BASED CRIMINOLOGICAL FORECASTING WHEN THE QUALITY OF THE RAW DATA DESCRIPTION IS INSUFFICIENT

Oleg G. Demenchenok1, Sergej A. Baranov 2

1East-Siberian Institute of the Ministry of Internal Affairs of the Russian Federation, Russia, Irkutsk

• ² Irkutsk Institute (branch) All-Russian State University of Justice, Russia, Irkutsk

  • ¹     asksystem@yandex.ru

  • ²     barss1962@mail.ru

Introduction: It is noted that criminological forecasting based on the trend model, having a number of indisputable advantages in comparison with other types of criminological forecasting, has significant disadvantages - the impossibility of ensuring the specified accuracy of the forecast, as well as limited forecasting capabilities in case of insufficient accuracy of the description of the observed data. The article explores the possibilities of improving the quality of data description when building trend models.

Materials and Methods: the study is based on reference data on the state of crime and methods of mathematical statistics.

The Results of Study: an approach to trend-based criminological forecasting with insufficient quality of initial data description is proposed, based on changing the functional dependence of the model and reducing the influence of anomalous data The proposed approach is implemented to solve the problem of short-term forecasting of the number of registered crimes in the Republic of Buryatia. It was possible to improve the quality of data description by 25% and to obtain a fairly accurate interval forecast estimation.

It is also shown that interval forecasting provides more complete and reliable information for decision-making and risk assessment, so it is preferable to point forecast estimation.

Findings and Conclusions: based on the study, the authors believe it is possible to recommend a trend model to improve the quality of data description:

• -    analysis of the quality of the description of data in various forms of functional dependence of the trend model by comparing the coefficients of determination and evaluating the accuracy of the forecast;

• -    verification of the presence of abnormal data with their subsequent exclusion from consideration or reduction of their impact by changing the observation interval.

В настоящее время отмечается возросшая востребованность прогнозирования как средства обеспечения управленческой деятельности органов внутренних дел.

Роль прогнозирования в управлении и планировании деятельности органов внутренних дел заключается в предсказании и анализе возможных преступлений и правонарушений. Прогнозирование позволяет определить вероятность совершения преступлений в определенных районах, а также показатели динамики преступности в будущем. Кроме того, прогнозирование помогает при разработке превентивных программ. Оно позволяет анализировать текущую ситуацию, выявлять тенденции и предсказывать возможные изменения в количестве преступлений, что помогает органам внутренних дел адаптировать свои действия в соответствии с изменяющимся окружением и эффективно использовать имеющиеся ресурсы.

Таким образом, прогнозирование играет важную роль в управлении и планировании деятельности органов внутренних дел, помогая более эффективно бороться с преступностью и обеспечивать безопасность граждан.

По сравнению с другими видами криминологического прогнозирования прогнозирование на основе трендовой модели обладает рядом бесспорных достоинств:

• 1.    Простота и понятность. Трендовая модель предполагает анализ и прогнозирование данных на основе временных трендов, что делает ее простой в использовании и понятной для лиц, принимающих решение.

• 2.    Высокая точность прогноза на короткий или средний срок. Трендовая модель основана на предположении об инерционности социальных процессов. Поэтому, когда динамика процесса сохраняется, трендовая модель может достичь высокой точности прогнозирования для ближайшего будущего.

• 3.    Помощь в выявлении долгосрочных тенденций. Трендовая модель может помочь выявить долгосрочные тенденции, например, рост или снижение преступности на протяжении нескольких лет.

• 4.    Быстрота и эффективность. Трендовая модель позволяет быстро анализировать и предсказывать данные на основе имеющихся трендов. Это может быть полезно в случае необходимости принятия оперативных решений.

• 5.    Возможность для анализа и идентификации выбросов (аномальных данных). Трендовая модель определяет характер изменения данных, освобожденный от случайных колебаний. Это позволяет быстро выявлять аномалии или выбросы в данных о преступности (например, не укладывающиеся в модель чрезмерно высокие значения).

Трендовая модель – эффективный инструмент краткосрочного и среднесрочного прогнозирования – помогает выявить долгосрочные тенденции и может быть полезной для оперативных решений и анализа данных о преступности.

Вместе с тем прогнозирование на основе трендовой модели не лишено и недостатков. Наиболее существенными недостатками трендовой модели является невозможность обеспечения заданной точности прогноза, а также то обстоятельство, что прогнозирование может оказаться невозможным вследствие недостаточной точности описания наблюдаемых событий или неподтверждения случайности ошибок аппроксимации.

Рассмотрим криминологическое прогнозирование на основе тренда при недостаточной точности описания моделью исходных данных.

Универсальной характеристикой точности описания моделью данных является коэффициент детерминации. Коэффициент детерминации R2 (R-квадрат) представляет собой меру того, насколько хорошо модель описывает вариацию исходных данных. Значение R-квадрат может варьироваться от 0 до 1, где 1 означает идеальное описание данных моделью. В общем случае, чем ближе значение R-квадрат к 1, тем лучше модель описывает исходные данные. Из определения коэффициента детерминации следует, что его численное значение отражает долю общей вариации результирующего признака (исходных данных), объясняемую изменением функции регрессионной модели [1, с. 402].

Точное значение коэффициента детерминации, при котором можно говорить о качественном описании данных, зависит от конкретного контекста решаемой задачи и предметной области исследования. Как правило, трендовые модели с коэффициентом детерминации R² < 0,5 не используют для прогнозирования ввиду недостаточного качества описания исходных данных (модель объясняет менее половины вариации данных). Коэффициент детерминации R² > 0,8 свидетельствует о достаточно хорошем качестве описания трендовой моделью исходных данных.

Однако далеко не всегда удается подобрать модель с коэффициентом детерминации, большим 0,8.

Среди факторов, влияющих на качество описания данных трендовой моделью, можно выделить:

• 1.    Вид функциональной зависимости. Выбор функциональной зависимости трендовой модели может существенно влиять на качество описания данных. Качество описания данных определяется тем, насколько точно модель предсказывает значения зависимой переменной на основе независимой переменной или набора переменных.

• 2.    Влияние выбросов или аномальных данных. Выбросы или аномалии могут оказывать существенное влияние на модель, причем их влияние на модель может быть различным в зависимости от того, находятся ли они в середине или на краях интервала данных.

Если выбрана правильная функциональная форма, то модель будет лучше аппроксимировать реальные данные и предсказывать значения зависимой переменной с минимальной ошибкой. В таком случае качество описания данных будет высоким.

Однако если неправильно выбрана функциональная зависимость, то модель может недостаточно точно предсказывать значения зависимой переменной. В данном случае, качество описания данных будет низким, и модель не будет хорошо согласовываться с наблюдаемыми данными.

Поэтому важно выбирать функциональную зависимость трендовой модели с учетом особенностей данных и проводить анализ качества описания данных при различных формах функциональной зависимости путем сравнения коэффициентов детерминации и оценки точности прогноза.

Правильный выбор функциональной зависимости трендовой модели можно рассматривать как один из способов улучшения качества описания данных.

Если выбросы находятся в середине интервала данных, то они могут значительно искажать статистики и меры центральной тенденции, такие как среднее, или медиана. Это, в свою очередь, может повлиять на параметры модели, основанные на этих статистиках, например, на регрессионные коэффициенты. Выбросы на краях интервала данных могут оказывать меньшее влияние, так как они находятся далеко от соседних наблюдений.

Чтобы улучшить соответствие модели данным, можно попробовать исключить аномальные данные из рассмотрения или изменить интервал наблюдения таким образом, чтобы аномальные данные оказались на краях интервала.

Попробуем разобраться, как можно провести криминологическое прогнозирование при недостаточной точности описания моделью исходных данных на примере краткосрочного прогнозирования количества зарегистрированных преступлений в республике Бурятия (далее – количество преступлений). Сведения о фактическом количестве совершенных в республике Бурятия преступлений доступны в отчетах «Состояние преступности в России», размещенных на официальном сайте МВД России1.

В предыдущей статье авторами предложена технология анализа трендовых моделей, позволяющая выбрать для криминологического прогнозирования лучшую по точности прогноза модель на основе оценок качества модели и ошибки прогноза [2, с. 134]. Попробуем применить эту технологию для решения данной задачи.

Для описания динамики количества зарегистрированных преступлений в республике Бурятия в 2010-2022 годах методом регрессионного анализа при помощи программы Microsoft Excel получены следующие трендовые модели (показательная и модифицированная показательная модели приводились к линейному виду при помощи логарифмирования):

у = - 0,43345 х + 26,45

линейная;

квадратичная;

кубическая;

показательная;

модифицированная показательная;

у = - 0,05145 х² + 0,28689 х + 24,649

у = - 0,0051 х³+0,05569 х² - 0,3356х +25,51

у = 26,621 • 0,9813 х у = 25,61-0,319 7• 1,254 7 х где y - количество преступлений (в тысячах), x - номер года (х = 1 для 2010 года). Исходные данные и результаты расчета приведены в таблице 1.

Исходные данные и результаты расчета по трендовым моделям

Таблица 1

Год	Количество преступлений (тысяч)
	Факт	расчет по модели
		линейная	квадратичная	кубическая	показательная	модифицированная показательная
2010	26,51	26,016	24,884	25,221	26,122	25,209
2011	24,137	25,583	25,017	25,017	25,632	25,106
2012	23,507	25,149	25,047	24,863	25,152	24,978
2013	23,765	24,716	24,973	24,728	24,681	24,817
2014	24,592	24,283	24,797	24,583	24,218	24,615
2015	27,797	23,849	24,518	24,396	23,764	24,362
2016	23,479	23,416	24,136	24,136	23,319	24,044
2017	23,61	22,982	23,651	23,773	22,882	23,645
2018	23,511	22,549	23,063	23,278	22,453	23,145
2019	22,131	22,115	22,373	22,617	22,033	22,517
2020	20,639	21,682	21,579	21,763	21,620	21,729
2021	20,77	21,248	20,682	20,682	21,215	20,740
2022	19,955	20,815	19,683	19,346	20,817	19,499
R2	1,000	0,578	0,667	0,676	0,563	0,667

В нижней строке таблицы 1 приведены значения коэффициентов детерминации. Полученные значения R² меньше 0,8. Это означает, что ни одна из моделей не обеспечивает достаточно хорошего качества описания исходных данных.

Одной из причин недостаточного качества описания данных может являться неверно выбранная функциональная зависимость. Функциональная зависимость трендовой модели определяет форму графика в виде определенной математической функции. Например, если мы используем линейную трендовую модель, то график будет представлять собой прямую линию. Если используется квадратичная трендовая модель, то график будет иметь форму параболы. Если данные имеют сложную форму или отсутствует явная зависимость, то выбор для модели математической зависимости может быть сложным. Использование альтернативной функциональной зависимости потенциально способно улучшить качество описания исходных данных.

Проверим, смогут ли другие трендовые модели улучшить качество описания данных. В качестве альтернативных форм уравнения регрессии применяются: степенная, логарифмическая, комбинация линейной и логарифмической, функция Торнквиста, логистическая (сигмоидальная) функция, гипербола, а также комбинация линейной функции и гиперболы [3, с. 27, с. 39, с. 54]. Следует отметить, что для альтернативных форм тренда методика расчета средних ошибок и доверительных границ прогноза развита недостаточно [4, с. 193]. Данное обстоятельство означает невозможность оценки доверительного интервала при прогнозировании на основе альтернативных трендовых моделей.

Числовые значения коэффициентов альтернативных трендовых моделей:

y = 26,742 x ⁰¹⁷⁷⁵                    - степенная;

y = 26,74 7 - 1,9202 In x             - логарифмическая;

y = 25,808 - 0,70626x + 1,4708 In x   - комбинация линейной и логарифмической;

y = =22,416x / ( x - 0,1666)          - функция Торнквиста;

y = 1 / ( 0,04348 - 0,0159 e^-x )         - логистическая функция;

y = 22,2 7+4,6848 / x                - гипербола;

y = 27,001 - 0,4808 x - 0,93053 /x   - комбинация линейной и гиперболы.

Результаты расчета по альтернативным трендовым моделям приведены в таблице 2.

Результаты расчета по альтернативным трендовым моделям

Таблица 2

Год	Количество преступлений (тысяч)
	факт	расчет по модели
		степенная	логарифмическая	линейная и логарифмическая	Торнк-виста	логистическая	гипербола	линейная и гипербола
2010	26,51	26,742	26,747	25,102	26,899	26,571	26,954	25,598
2011	24,137	25,344	25,416	25,415	24,454	24,194	24,612	25,582
2012	23,507	24,560	24,637	25,305	23,735	23,423	23,831	25,256
2013	23,765	24,018	24,085	25,022	23,391	23,152	23,441	24,853
2014	24,592	23,606	23,656	24,644	23,189	23,054	23,207	24,419
2015	27,797	23,275	23,306	24,206	23,057	23,018	23,050	23,969
2016	23,479	22,999	23,010	23,726	22,963	23,005	22,939	23,510
2017	23,61	22,762	22,754	23,216	22,893	23,000	22,855	23,046
2018	23,511	22,555	22,528	22,683	22,839	22,998	22,790	22,578
2019	22,131	22,372	22,325	22,132	22,796	22,997	22,738	22,108
2020	20,639	22,207	22,142	21,566	22,761	22,997	22,695	21,635
2021	20,77	22,058	21,975	20,988	22,732	22,997	22,660	21,162
2022	19,955	21,921	21,821	20,399	22,707	22,997	22,630	20,687
R2	1,000	0,426	0,437	0,606	0,282	0,206	0,294	0,582

Для рассматриваемого примера альтернативные функциональные зависимости не способны улучшить качество описания данных: коэффициент детерминации не превышает 0,606, что хуже соответствующего показателя для квадратичной, кубической и модифицированной показательной модели.

Недостаточное качество описания наблюдаемых событий также может обусловлено выбросами (аномальными данными). С помощью трендовой модели можно выявить аномальные данные, сравнивая фактические значения с прогнозными значениями, которые модель предсказывает на основе тренда. Если фактические значения сильно отклоняются от прогнозных значений, то это может указывать на наличие аномалий. Для наглядности на рис. 1 совместим фактические и прогнозные значения.

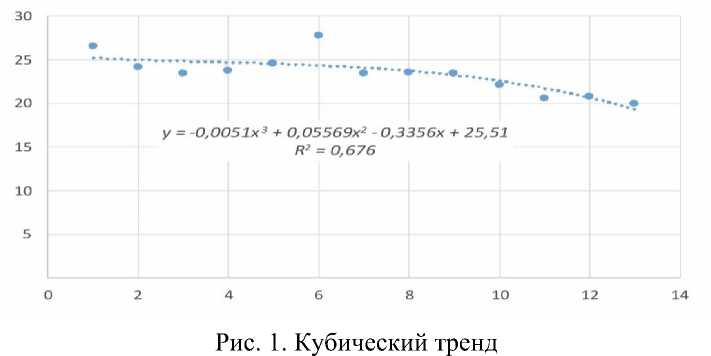
Сравнивая фактические значения с прогнозными, легко заметить, что максимальное расхождение между ними соответствует шестому временному интервалу. Это расхождение равно 3,4, что почти в четыре раза больше средней величины расхождения 0,86. Такое расхождение можно рассматривать как свидетельство аномальности данных. Поскольку аномалия данных находится почти в середине интервала, то она оказывает существенное влияние на параметры трендовых моделей. Примерно в полтора раза больше среднего расхождение значений в точках с координатами по горизонтальной оси 1 и 3.

Мы можем сократить интервал наблюдения, отбросив часть наиболее ранних данных. Предположим, что требуется подготовить прогноз на срок от одного до трех лет. Учитывая, что интервал наблюдения как минимум в три раза должен превышать интервал прогноза, примем длину интервала наблюдения равной девяти годам, что соответствует данным с 2014 по 2022 гг.

В этом случае отбрасываются данные за первые четыре года наблюдения, в том числе данные за 2010 и 2012 гг. с расхождением в полтора раза больше среднего. Аномальное значение за 2015 г. оказывается на краю измененного интервала, что уменьшает его влияние на параметры моделей.

Для принятого интервала наблюдения проведен подбор параметров трендовых моделей, пригодных для интервальных оценок прогноза:

у = - 0,7798 t + 26,842 ;

у = - 0,01458 t² - 0,633961 + 26,574 ;

у = 0,0029 t³ - 0,4502 t 2 +1,2015t +24,658 ;

у = 27,047 • 0,9667 ;

у = 28,8 72 - 2,2453 • 1,1831 t ;

где t — номер года (t = 1 для 2014 года).

Результаты расчета приведены в таблице 3.

Результаты расчета для измененного интервала наблюдения

Таблица 3

Год	Количество преступлений (тысяч)
	Факт	расчет по модели
		линейная	квадратичная	кубическая	показательная	модифицированная показательная
2014	24,592	26,062	25,926	25,438	26,146	26,215
2015	27,797	25,282	25,248	25,492	25,275	25,729
2016	23,479	24,502	24,541	24,994	24,433	25,153
2017	23,61	23,722	23,805	24,119	23,619	24,472
2018	23,511	22,943	23,040	23,040	22,833	23,667
2019	22,131	22,163	22,246	21,932	22,072	22,713
2020	20,639	21,383	21,422	20,969	21,337	21,586
2021	20,77	20,603	20,569	20,325	20,626	20,251
2022	19,955	19,823	19,687	20,175	19,939	18,672
R2	1,000	0,777	0,778	0,804	0,773	0,757

За счет изменения интервала наблюдения удалось ослабить влияние аномальных данных. Примерно на 25% увеличено значение коэффициентов детерминации трендовых моделей, благодаря чему достигнута достаточная точность описания наблюдаемых событий. Коэффициенты детерминации для всех рассматриваемых моделей превысили 0,75. Максимальное значение R² = 0,804 получено для кубической модели (соответствующий тренд приведен на рис. 2).

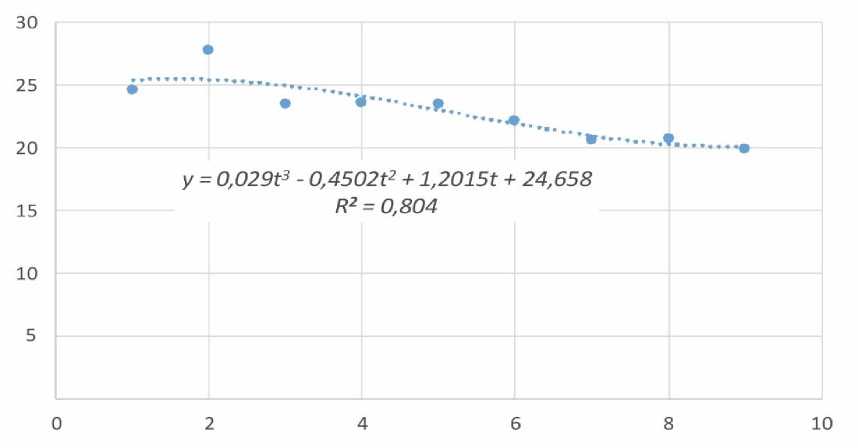
Рис. 2. Кубический тренд для измененного интервала наблюдения

Оценку качества трендовых моделей следует дополнить оценкой значимости входящих в уравнение модели коэффициентов. Статистическим инструментом такой оценки является критерий Стьюдента (t-критерий Стьюдента, также известный как t-тест). Он позволяет определить, насколько существенно отличаются оцененные коэффициенты от нуля. Если абсолютное значение критерия Стьюдента превышает критическое значение, то это подтверждает ненулевое значение оцененного коэффициента уравнения регрессии. Если абсолютное значение критерия Стьюдента меньше критического значения, то включение в модель регрессии соответствующей переменной не обоснованно, а сама модель непригодна для прогнозирования. Проверка по критерию Стьюдента для уровня значимости 0,05 не подтвердила статистическую значимость коэффициентов квадратичной и кубической модели, и они исключены из рассмотрения.

Далее проведена проверка случайности колебаний ошибок аппроксимации по методу поворотных точек, проверка соответствия распределения ошибок нормальному закону, а также равенства нулю средней разности фактических и расчетных данных.

Проверки подтвердили пригодность для прогнозирования линейной, показательной и модифицированной показательной модели. Результаты точечной оценки прогноза по этим моделям приведены в таблице 4 (для 2023 года t = 10 ).

Результаты точечной оценки прогноза

Таблица 4

Год	Прогноз количества преступлений (тысяч)
	линейная модель	показательная модель	модифицированная показательная модель
2023	19,044	19,275	16,805
2024	18,264	18,633	14,595
2025	17,484	18,012	11,980

Переход от точечной оценки к интервальному прогнозу базируется на расчете средней ошибки прогноза линейного тренда [4, с. 195]:

m =а (l+l/n+tk2/^’,5, где о - среднеквадратическое отклонение расчетных и фактических данных на интервале наблюдения; n – длина интервала наблюдения (для интервала с 2014 по 2022 года n =9); tk, - номер года, отсчитываемого от середины интервала наблюдения; Z- сумма квадратов номеров годов интервала наблюдения, отсчитываемых от его середины.

Найдем ошибку прогноза на 2023 г. Середина интервала наблюдения соответствуе т 2018 году, следовательно t k =5 ,

£ = ( - 4)² + ( - 3) 2 + ( - 2)² + ( - 1 )² + 0 2 + 1 2 + 2 2 + 3 2 + 4 ² =60 .

Получено расчетное значение средней ошибки прогноза по линейной модели m = 1,333 . Для расчета доверительного интервала прогноза полученное значение следует умножить на величину t - критерия Стьюдента для соответствующей вероятности и степени свободы (разнице между n и количеством параметров модели 9 - 2=7) .

Тогда с вероятностью 90 % количество преступлений в 2023 г. окажется в доверительном интервале:

19,044 ± 1,333 - 1,895 = 16,518^21,569 .

Ширина доверительного интервала 21,569 - 16,518 = 5,051 .

Логарифмированный вид показательной модели ln(y) = 3,29 76 - 0,03388 t представляет собой линейную модель. Расчет по формулам для линейного тренда приводит к доверительному интервалу:

2,9588 ± 0,053 ⋅ 1,895 = 2,859 …3,059.

Доверительный интервал показательной модели:

exp ( 2,859 )    exp ( 3,059 ) = 17,441.21,302 .

Ширина доверительного интервала 21,302 - 17,441 = 3,861 . Это свидетельствует о более высокой точности прогноза, так как ширина доверительного интервала на 24% меньше ширины аналогичного интервала линейной модели.

Расчетное значение средней ошибки прогноза для логарифмированного вида модифицированной показательной модели m = 0,52. Это практически на порядок превышает значение для показательной модели m = 0,053. Причиной является существенно большее среднеквадратическое отклонение σ (соответственно 0,421 и 0,043). Следствием является крайне низкая точность прогноза по модифицированной показательной модели:

доверительный интервал для логарифмированного вида модели ln( 28,872 - у ) = 0,8088+0,1682 t :

2,4905 ± 0,520 - 1,895 = 1,505 ...3,476 ;

доверительный интервал модели:

• 28,8 72 - exp ( 1,505 ) ... 28,8 72 - exp ( 3,476) = -3,5.24,396.

С практической точки зрения такой прогноз бесполезен ввиду того, что охватывает почти все возможные значения.

Данный пример убедительно иллюстрирует преимущество интервального прогнозирования по сравнению с точечной оценкой.

В точечной оценке прогноза мы получаем только одно значение, которое считается наиболее вероятным. Однако эта оценка может быть неточной или иметь большую погрешность, что может привести к неправильным управленческим решениям.

Интервальное прогнозирование, с другой стороны, предоставляет диапазон значений, в котором с высокой вероятностью находится истинное значение прогнозируемой величины. Это позволяет учитывать неопределенность и степень надежности прогноза. Определение интервала прогноза основывается на статистических методах и учитывает вариативность данных и размер интервала наблюдения.

Преимущество интервального прогнозирования по сравнению с точечной оценкой заключается в том, что интервальный прогноз предоставляет более полную информацию о неопределенности и надежности прогноза.

В рассматриваемом примере интервальный прогноз выявил:

• -    очень большую погрешность и, как следствие, непригодность прогноза по модифицированной показательной модели;

• -    большую точность прогноза по показательной модели (при том, что качество описания исходных данных линейной моделью выше).

Таким образом, интервальный прогноз позволяет лучше оценить риски и принять более обоснованные решения. Кроме того, он полезен при сравнении прогнозов разных моделей или методов, так как позволяет оценить их точность и стабильность.

Результаты интервального прогнозирования по показательной модели для вероятности 90% сведены с таблицу 5.

Таблица 5

Результаты интервального прогнозирования

Год	Прогноз количества преступлений (тысяч)
	точечная оценка прогноза	доверительный интервал
2023	19,275	17,441…21,302
2024	18,633	16,762 …20,713
2025	18,012	16,099 …20,153

Рассмотренный пример подтверждает эффективность предложенного подхода к криминологическому прогнозированию для случая недостаточной точности описания моделью исходных данных. Удалось на 25 % улучшить качество описания данных и получить достаточно точную интервальную оценку прогноза.

Также показано, что интервальное прогнозирование предоставляет более полную и надежную информацию для принятия решений и оценки рисков, поэтому оно предпочтительнее точечной оценки прогноза.

На основе проведенного исследования авторы считают возможным рекомендовать для решения подобных задач:

– анализ качества описания данных при различных формах функциональной зависимости трендовой модели путем сравнения коэффициентов детерминации и оценки точности прогноза;

– проведение проверки наличия аномальных данных с последующим исключением их из рассмотрения или уменьшением их влияния за счет изменения интервала наблюдения.