Критерии оптимального управления и LQR-оптимизация в электроприводе

Введение . Промышленные электромеханические комплексы (тиристорный преобразователь-двигатель – ТП-Д) всегда устойчивы по всем переменным состояния, если они являются элементами разомкнутых систем управления. В замкнутых системах управления эти объекты также рассматриваются как устойчивые по переменным вход–выход и могут обладать внутренней неустойчивостью, если нет ограничений на переменные состояния, управления и скорость их изменения.

Для одной и той же устойчивой системы существует множество стабилизирующих воздействий, и необходимо выбирать среди них оптимальное с точки зрения критерия (функционала) качества, который должен иметь физический смысл. Такое управление называется оптимальным. В общем случае для решения задачи оптимизации необходима информация об объекте управления в виде алгебраических и дифференциальных уравнений, связывающих входные, выходные переменные и переменные состояния; о среде функционирования объекта управления и ограничениях на все переменные состояния и управления; о показателе оптимальности (критерии качества, оптимальности, выгоды). Если эта информация доступна, можно выбрать метод оптимизации и ре- шить задачу оптимального управления.

Цель работы. Анализ критериев оптимального управления и методов оптимизации.

При анализе систем управления обычно рассматривают два режима работы – статический и динамический. Поэтому все методы оптимизации делятся на статические и динамические [1, 2]. Объект управления (электрический двигатель) находится в состоянии непрерывного движения под действием различных внешних и внутренних факторов. Следовательно, оценка результата управления дается за время управления Т , и это задача динамической оптимизации.

С помощью методов динамической оптимизации решаются задачи, связанные с распределением ограниченных ресурсов для достижения комплекса конкурирующих целей на протяжении некоторого промежутка времени, а целевая функция записывается в виде интегрального функционала. Ограничения накладываются как на переменные управления, так и на переменные состояния. Обычно это неравенства или интегральные ограничения, так как приходится иметь дело с конечными ресурсами источников энергии или с необходимостью ограничения пределов изменения некоторого параметра в процессе управления, являющегося функцией переменных состояния и управления (например, ускорение, угол поворота вала исполнительного механизма и т.д.) [1, 3].

Анализ и синтез систем управления выполняется во временной, частотной областях и в пространстве состояний. В первом случае общепринятыми считаются интегральные критерии миниму- ма расхода энергии на управление th и максимального быстродействия

∫U(t)·i(t) dt to

→min

J 2=

∫1dt =   - to to

= →min.

Рассматриваемые критерии для своей реализации требуют источников бесконечно малой и бесконечно большой мощности соответственно. Следовательно, возникает задача нахождения оптимального закона управления, удовлетворяющего наилучшим образом двум противоречивым критериям.

Для выработки такой стратегии управления предварительно рассчитывают оптимальные управляющие воздействия u 1 ^* и u 2 ^* , обеспечивающие, при принятых ограничениях, экстремум функционалам Ј1= J1^* и J2 = J2^*. Их находят методами вариационного исчисления. Далее рассматривается критерий оптимального управления

= ∙| ∗ ^∗ |+ ∙| ∗ ^∗ | , (3)

где а и в — весовые коэффициенты, определяемые стратегией управления. В функционале (3) при коэффициентах а и в стоят абсолютные значения величин. Это вызвано тем, что функционалы J1 ^* и J2 ^* могут достигать в точке экстремума либо максимум, либо минимум, а разности могут быть и положительными, и отрицательными. Управление, удовлетворяющее критерию (3), называется компромиссным [4].

Математическим аппаратом решения таких задач являются вариационные методы: классическое вариационное исчисление, принцип максимума Л.С. Понтрягина и динамическое программирование Р. Беллмана [1, 3, 5].

Для решения частных задач применяются критерии минимума тока, потребляемого электроприводом, минимума тепловых потерь в электродвигателе, а также известные в теории автоматического управления интегральные оценки качества переходного процесса:

минимум среднеквадратичного отклонения ε²(t)

Ж

J = |s2(t)dt ^ min;

улучшенный квадратичный критерий качества tк

J = j ts2 (t) dt

^ min

t ₀

и обобщённый интегральный критерий качества tk

2 .

x + Y i

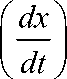
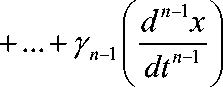
dt ^ min

J=J

t ₀

от квадратичных форм [6]. В последнем критерии x - выходная переменная; y i - весовые коэффициенты при квадратах производных i -го порядка от выходной координаты. Первое слагаемое запрещает длительное существование отклонения х от заданного, а последующие – длительное существование больших производных. Поэтому минимуму интеграла соответствуют достаточно быстрые и плавные переходные процессы. Имея дифференциальное уравнение замкнутой системы и задавая весовые коэффициенты, можно вычислить оптимальное значение функционала. Можно решить и обратную задачу.

Для оптимизации амплитудно-частотных характеристик (АЧХ) замкнутых систем управления электроприводом используют критерии амплитудного (МО), симметричного (СО) и компромиссного оптимумов (КО). Основное требование – максимальная близость АЧХ проектируемой системы к АЧХ идеального фильтра нижних частот, которая математически задается в виде dA2(ro)/dron = 0 при го = 0 (МО), dA2(ro)/dron ^ 0 при го ^ 0 (СО); п= 2, 4, 6....

Из технических устройств этим требованиям удовлетворяют фильтры Баттерворта второго и третьего порядков.

Управление объектом по критерию МО обеспечивает оптимальный переходный процесс при изменении задания и затянутый переходный процесс при изменении нагрузки, система управления является астатической по заданию и статической по возмущению. Системы с регуляторами, структура и параметры которых выбраны по критерию СО, имеют оптимальный переходный процесс при изменении нагрузки и неблагоприятный переходный процесс при изменении задания (перерегулирование до 43%), относительно небольшие запасы устойчивости по амплитуде и фазе, чувствительны к изменениям параметров объекта управления, являются астатическими как по заданию, так и по нагрузке. Таким образом, эти два критерия также являются противоречивыми. Устранить эти противоречия можно путем включения на вход системы СО низкочастотного фильтра (система с двумя степенями свободы) или выбирать регуляторы по критериям линейного и компромиссного оптимумов [7–10].

При решении задач оптимизации в пространстве состояний, когда линейная стационарная система задана векторно-матричными уравнениями

̇=   =   +   ;   =   , dt целесообразно представлять критерии (1) и (2) в виде квадратичных форм

и переходить к функционалам

∞∞

∫       →   ,    = ∫       → о                                    о

/б

∞

= ∫(    +      +2    )  →   ,

о

∞

= ∫(     +      +2    )  →   .

о

Закон управления u находится в форме линейной обратной связи [11–14] по переменным состояния x или по переменным выхода у , т.е.

u = ± Kx , u = ± Ky .

Такое управление минимизирует квадратичные критерии качества (6).

Здесь Q и R - симметричные положительно определённые матрицы размерностью [n x n] и [m x m] соответственно; К - матрица постоянных коэффициентов размерностью [m^n], на значения которых нет ограничений. Если входной параметр N опущен, он принимается нулевым.

Известно [13–15], что решение данной задачи, которая называется задачей линейной интегральной квадратичной оптимизации ( LQR-оптимизации ), в пространстве состояний определяется выражением

u = R^-1B^TPx , где матрица Р должна удовлетворять уравнению Рикатти А^ТР + РА - РВR^-1B^ТР + Q = 0.

Критерии (6) также противоречивы, так как для реализации первого слагаемого требуется источник бесконечно большой мощности, а для второго – источник бесконечно малой мощности. Это можно объяснить следующим: выражение

∞

=∫ является нормой II х|| вектора х, т.е. мерой его колебательности в процессе регулирования, и, следовательно, принимает меньшие значения в быстрых переходных процессах с меньшей колебательностью;

выражение

∞

=∫

о является мерой количества энергии, используемой для управления, это штраф за энергетические затраты системы [14, 15].

От весовых матриц Q , R и N зависят ограничения соответствующих координат. Если какой-либо элемент этих матриц равен нулю, то соответствующая координата ограничений не имеет. На практике выбор значений матриц Q , R , N осуществляется методом экспертных оценок, проб, ошибок и зависит от опыта и знаний инженера-проектировщика.

Для решения таких задач в MATLAB имеются операторы

[K,S,E] = lqr(A,B,Q,R,N) и [K, S, E] = lqry(Ps,Q,R,N) , которые минимизируют функционалы (6), (7) по вектору состояния х или по вектору выхода y [16]. Модель объекта управления Рs = ss(A,B,C,D). Результатом расчёта является матрица К оптимальных обратных связей по переменным состояния х, решение уравнения Риккати S и собственные значения

Е = eig( A – BK ) замкнутой системы управления. Составляющие функционала Jx = х 0^TP₁ х о и Ju = х 0^TP₂ х о, где х0 – вектор начальных условий; P1 и Р2 – неизвестные матрицы, которые являются решением матричных уравнений Ляпунова [13]. Они находятся с помощью функций P 1 =lyap ( NN,Q ) и P 2 = lyap ( NN,K ^Т RK ) , NN =(A+BK)^Т .

Рассмотрим синтез линейно-квадратичного регулятора, удовлетворяющего критерию (6) для объекта управления [7, 17], заданного в пространстве состояний матрицами:

-100

А = [143,678 0

-16,667  -195,402

1,046        0

2300       1 0  0

]; в = [  0  ]; с =[0  1  0]; D = 0.

0    001

В качестве переменных состояния рассматриваются: х1 – напряжение преобразователя, В; х2 – ток двигателя, А; х3 – угловая скорость, с-1.

Это система ТП – ДПТ с НВ: двигатель Р ном = 30 кВт; U ном = 220 В; I ном = 147 А; ω ном = 157 с^-1; ω 0 = 169 c^-1; ω max = 187 c^-1; момент сопротивления номинальный М ном = 150 Н*м; кратность пускового тока = 2; тиристорный преобразователь: U ном = 230 В; U y = 10 B; I ном = 300 А; кратность кратковременной перегрузки по току =1,2.

При решении задачи принимаем матрицу Q диагональной.

В результате моделирования установлено, что минимальные значения элементов матриц R = 84 , а Q = diag [0.01 0.01 0.01] . В этом случае наблюдается монотонный переходный процесс угловой скорости двигателя (рис. 1). При R = 840 Q = [0.01 0.01 0.01] переходный процесс (рис. 2) соответствует критерию МО. Расчет матриц Р1 и Р2 выполнен при х0 = [220 147 162].

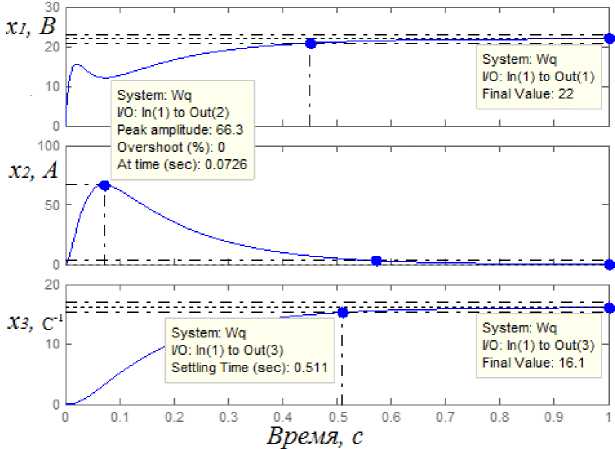
Рис. 1. Переходные функции в системе управления при R = 84, Q = [0.01 0.01 0.01]. Jx = 697,8; Ju = 229,7

Peak amplitude: 23 Overshoot (%): 0.476 At time (sec): 0.399

System: Wq l/O:ln(1)toOut(1)

Settling Time (sec): 0.1

System: Wq

I/O: ln(1)to Out(1)

Final Value: 22.9

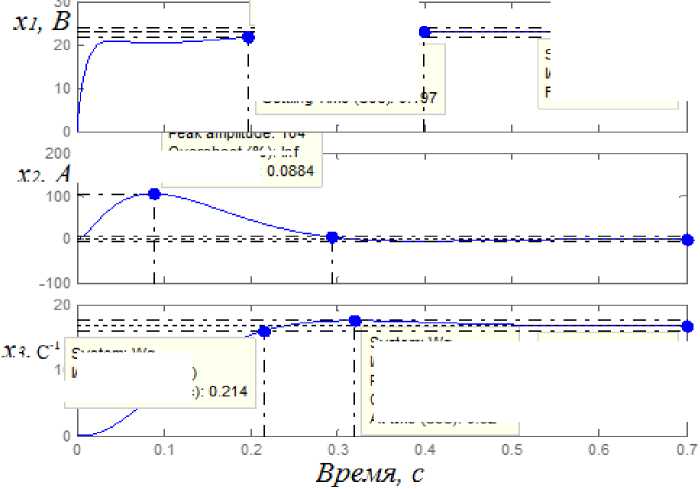
System: Wq

I/O: ln(1) to Out(3)

Peak amplitude: 17.6

Overshoot (%): 4.33

At tine (sec): 0.32

System: Wq I/O: ln(1)to Out(3) Final Value: 16.8

Рис. 2. Переходные процессы в системе управления при R = 840, Q = [0.01 0.01 0.01]. Jx = 1,25*10³; Ju = 112,6

Overshoot (%): Inf At time (sec):

System: Wq

I/O: ln(1)to Out(3)

Settling Time (sec

Соответствующим выбором матриц R и Q можно уменьшить пусковой ток двигателя до допустимых значений, равных (2–2,5) I ном (рис. 3). Например, при R = 840 и Q = [0.01 0.88 0.01] его значение равно 292 А, а время переходного процесса при этих условиях – 1,57 с.

При моделировании использован программный код на языке MATLAB, представленный в листинге 1 (прил.).

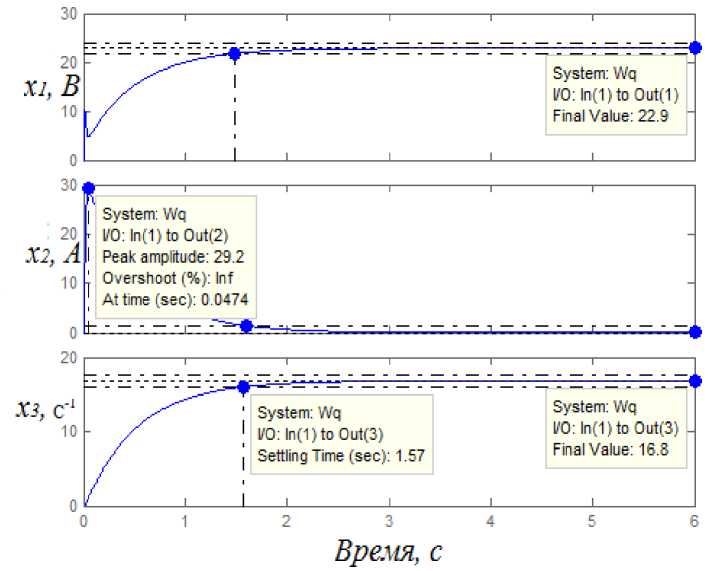
Рис. 3. Переходные процессы при допустимом пусковом токе Jx = 2,05*104; Ju = 1,47*104

Во всех рассмотренных случаях обратные связи по напряжению и току являются отрицательными, а по скорости – положительными, что нежелательно по требованиям устойчивости. Кроме того, синтезированная система является астатической по заданию и статической по нагрузке. Поэтому рассмотрим синтез ПИ-регулятора в пространстве состояний с дополнительной переменной состояния х 4 – коэффициентом передачи интегратора [9, 10].

Исходную информацию представим в виде матриц:

=[

143,678 0

0 -16,667 1,046 0

-195,4020

] ;     =[  ⁰  ] ; C =eye(4); D = 0.

Переходные процессы по заданию, соответствующие критерию МО, получены при R = 100, q 11 = q 22 = q 33 = 0.001 и q 44 = 200. На рисунке 4 представлены переходные процессы переменных состояния, подтверждающие астатизм системы по заданию и по нагрузке (листинг 2, прил.).

Для определения матрицы К в MATLAB есть две функции K=acker(A,B,s) и К = place (A,B,s) , где s – вектор-строка желаемых полюсов передаточной функции замкнутой системы управления. Первая команда может быть использована только для систем с одним входом по u при n≤5. Вторая не имеет таких ограничений, однако кратность полюсов не должна превышать ранг матрицы В [16]. Пример использования этих операторов приведен в листинге 3 (прил.).

Если задан диапазон изменений элементов матрицы К (многокритериальная задача оптимизации с ограничениями, задача достижения цели), её решение возможно с помощью функции

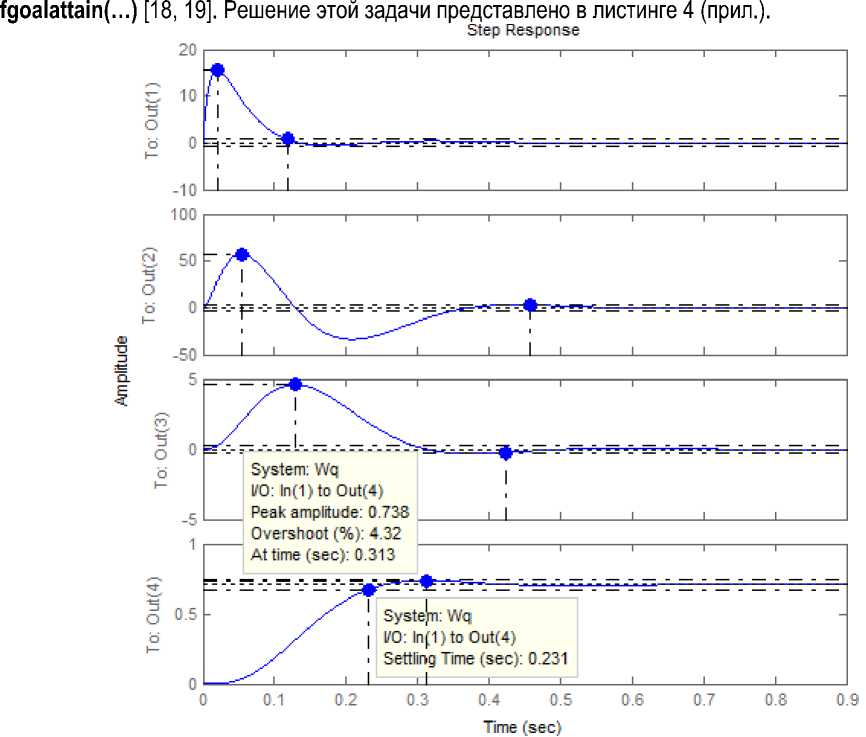
Рис. 4. Переходные процессы в системе с оптимальным LQR ПИ-регулятором

Выполним анализ полученных результатов путем сравнения динамических свойств трех систем управления: система с фильтром, регуляторы которой выбраны по критерию СО и МО; система с коррекцией по компромиссному оптимуму (регуляторы СО, МО, встречно-параллельная кор- рекция с выхода на вход реализована с помощью звена с передаточной функцией W(s) = 0,449(0,02s+1) и система с оптимальным LQR ПИ-регулятором. Структурные схемы этих систем в MATLAB+Simulink представлены на рисунках 5 и 6. На рисунках 7–10 показаны переходные процессы в рассматриваемых системах.

Очевидно, что система с оптимальными обратными связями более инерционна (рис. 7, 10) и имеет менее жесткую электромеханическую характеристику. В то же время переходный процесс соответствует теории МО, и она обладает внутренней устойчивостью по току якоря и напряжению источника питания (рис. 7–9, пусковой ток двигателя не более 2000 А, напряжение ТП не более 230 В). Из всех рассмотренных систем по результатам моделирования наилучшей по динамическим и электромеханическим свойствам следует считать систему компромиссного оптимума.

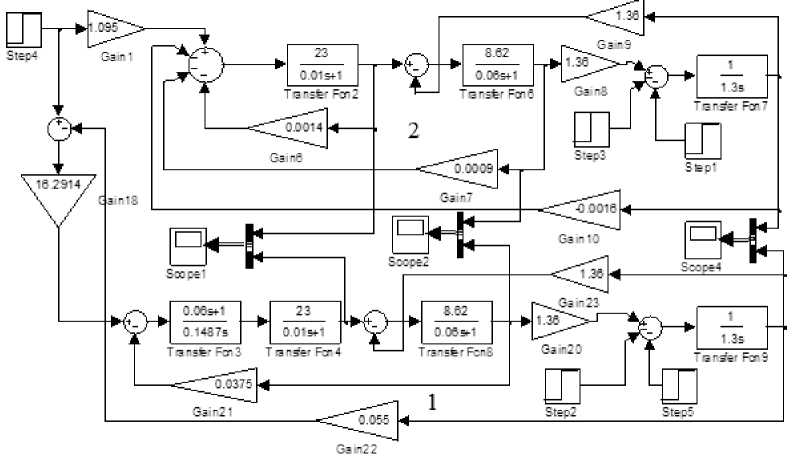
Рис. 5. Структурные схемы замкнутых систем управления: 1 – система с регуляторами МО-МО; 2 – система с оптимальными обратными связями

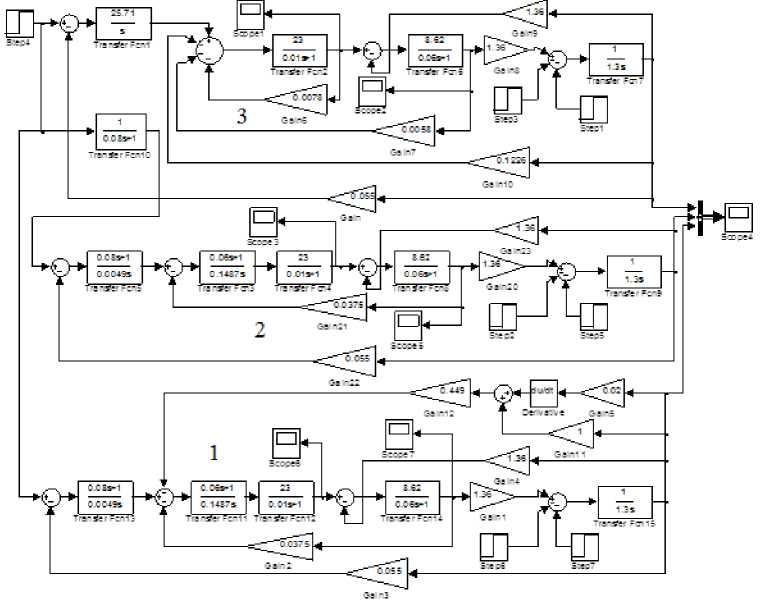
Рис. 6. Структурные схемы систем: 1 – система компромиссного оптимума;

2 – система СО-МО c фильтром; 3 – система с оптимальным LQR ПИ- регулятором

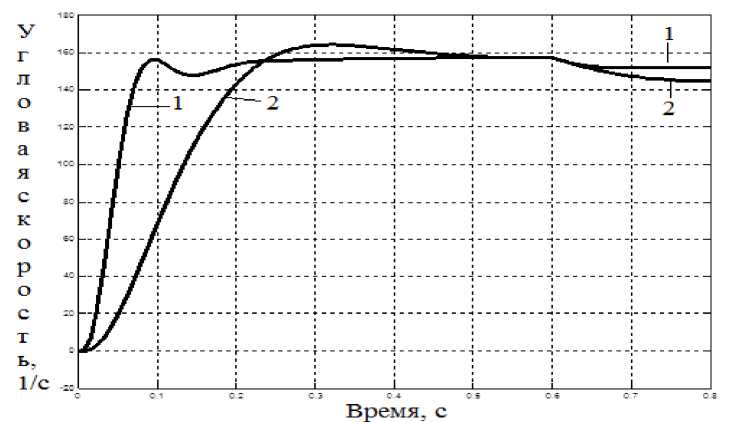
Рис. 7. Переходные процессы: 1 – система МО-МО; 2 – система с оптимальными обратными связями

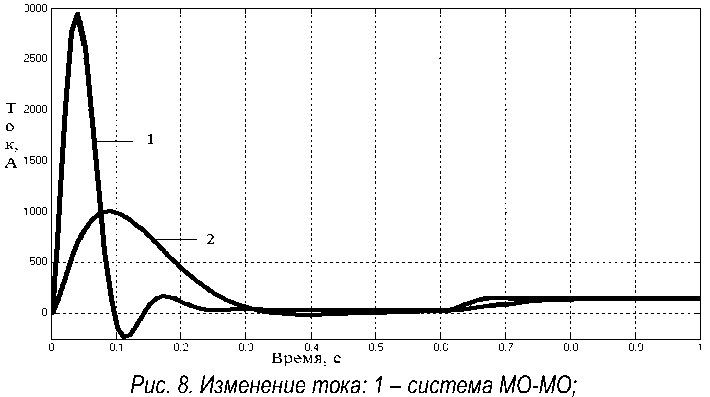
2 – система с оптимальными обратными связями

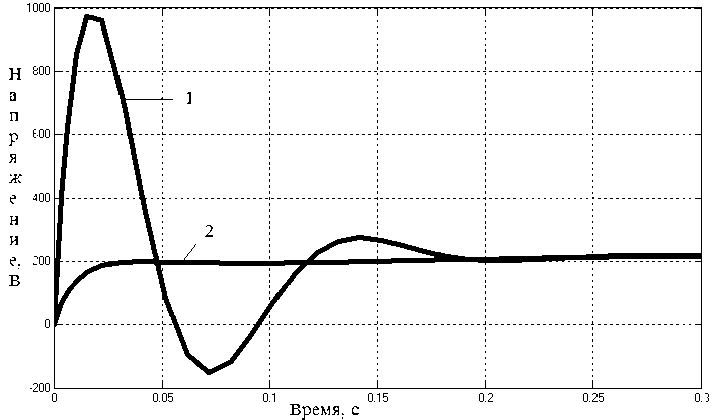
Рис. 9. Изменение напряжения преобразователя: 1 – система МО-МО; 2 – система с оптимальными обратными связями

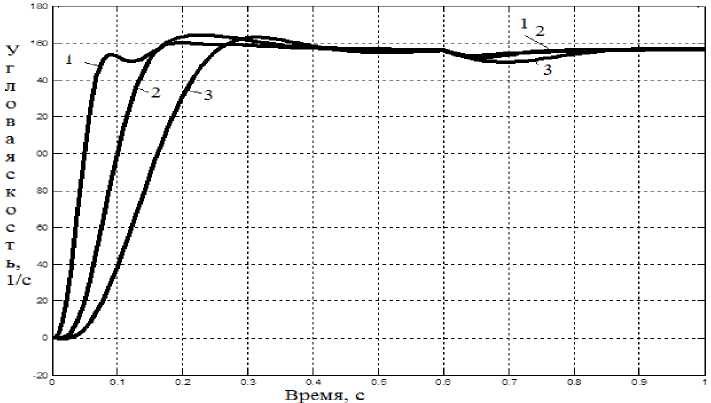
Рис. 10. Переходные процессы по скорости: 1 – система компромиссного оптимума; 2 – система СО – МО с фильтром; 3 – система с оптимальным LQR ПИ-регулятором

Выводы. На основании вышеизложенного делаем следующие выводы.

• 1.    Критерии минимума расхода энергии на управление и максимального быстродействия являются базовыми, все остальные критерии являются следствием этих критериев.

• 2.    Исследование объекта в пространстве состояний дает результаты, наиболее адекватные свойствам реального объекта управления (см. рис. 8 и 9).

• 3.    Регуляторы, структура и параметры которых выбраны в пространстве состояний, учитывают действие обратной связи по ЭДС, хотя и уступают в быстродействии системам с регуляторами МО, СО и КО (см. рис. 4, 7 и 10).

• 4.    Решение задач LQR-оптимизации позволяет рассчитывать коэффициенты жестких обратных связей, обеспечивающих критерий МО и прямой пуск двигателя без устройств плавного пуска (см. рис. 1, 2 и 3) как с ограничениями, так и без ограничений на вектор К .

В заключение следует отметить, что результаты моделирования нуждаются в проверке на реальных системах управления электромеханическими объектами.

Приложение

Листинги программ в MATLAB

Листинг 1

LQR- оптимальный синтез жестких обратных связей по переменным состояния

% Коэффициенты объекта

A=[-100 0 0;143.678 -16.667 -195.402;0 1.046 0];

B=[2300; 0; 0];

C=[1 0 0;0 1 0;0 0 1 ];

D=0;

% Матрицы весовых коэффициентов

R=840;

Q=[0.01 0 0;0 0.88 0;0 0 0.01];

% Синтез LQR-оптимального регулятора

[K,S,E]=lqr(A,B,Q,R)

% Вычисление составляющих функционала N=A-B*K;NN=N';

Wq=ss(N,B,C,D)

x0=[220; 147; 162];

Ct=C';

P1=lyap(NN,Ct*Q*C)

Kt=K';

x0t=x0';

Jx=x0t*P1*x0

P2=lyap(NN,Kt*R*K);

Ju=x0t*P2*x0

% Переходные процессы в системе step(Wq)

Синтез оптимального LQR ПИ-регулятора

A=[-100 0 0 0;143.678 -16.667 -195.402 0;0 1.046 0 0;0 0 1 0];

B=[2300; 0; 0;0];

C=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];

D=0;

R=100;

Q=[0.001 0 0 0;0 0.001 0 0;0 0 0.001 0;0 0 0 200];

[K,S,E]=lqr(A,B,Q,R)

N=A-B*K;NN=N’;

Wq=ss(N,B,C,D);

x0=[220; 147; 162; 0];

Ct=C’;

P1=lyap(NN,Ct*Q*C);

Kt=K’;

x0t=x0’;

Jy=x0t*P1*x0

P2=lyap(NN,Kt*R*K);

Ju=x0t*P2*x0

Wl=tf(Wq)

pole(Wl)

step(Wq)

Синтез оптимальных обратных связей

A=[-100 0 0 0;143.678 -16.667 -195.402 0;0 1.046 0 0;0 0 1 0];

B=[2300; 0; 0;0];

C=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];

D=0;

p=[-9.71+14.97i -9.71-14.97i -15.39 -99.72];

k=acker(A,B,p)

H=A-B*k;

Wss=ss(H,B,C,D);

step(Wss)

W=tf(Wss)

Листинг 2

Листинг 3

Листинг 4

Задача с ограничениями на вектор К

A=[-100 0 0;143.678 -16.667 -195.402;0 1.046 0];

B=[2300; 0; 0];

C=[1 0 0;0 1 0;0 0 1 ];

goal=[-99.67,-10.13+10.17i,-10.13-10.17i];

weight=abs(goal);

K0=[-0.002 -0.002 -0.002];

lb=repmat(-0.005,size(K0));

ub=repmat(0.005,size(K0));

options=optimset('Display','iter');

eigfun=@(K) sort(eig(A+B*K*C));

[K,fval,attainfactor,exitflag,output,lambda]=fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options);

K eigfun(K)

attainfactor options=optimset(options,'GoalsExactAchieve',3);

[K,fval,attainfactor,exitflag,output,lambda]=fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options);

K eigfun(K)

attainfactor

[Times,xvals]=ode45(@(u,x)((A+B*K*C)*x),[0,0.4],[220;147;162]);

plot(Times,xvals)

legend('x 1(t)','x 2(t)','x 3(t)','Location','best')

xlabel('t');

ylabel('x(t)');