Критическое растяжение межатомной связи в аморфных веществах под действием теплового давления и механического напряжения

1Г d 2U ) ₂ 1Г d 3U ) з x + 4  Г I x +4  Г I x ’

2 к dr ² )       61 dr )

r0

r0

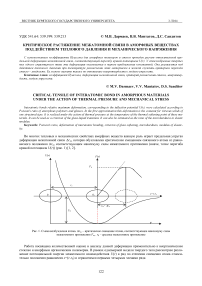
где r 0 – равновесное расстояние между атомами. Примем во внимание, что в точке минимума функции U ( r ) (рис. 1) первая производная равна нулю (dU/dr) r=r0 = 0. Далее, вводя обозначения

Г d ² U ) a = I I dr ²

\          7 r = r о

К Г d ³ U )

,

, b = -I —I dr 3

\          / r = rо приходим к следующему соотношению для потенциала U(x) двух смежных частиц [3]

U =

ax 2 bx 3

,

где a – гармонический, а b – ангармонический коэффициенты.

Сила межатомного взаимодействия f = -(dU/dx) выражается формулой

b

.

f = - ax + —x

В точке перегиба кривой U ( r ) величина силы взаимодействия атомов проходит через максимум (рис. 1). Отсюда критическое удлинение межатомной связи x m =( r m - r 0 ), соответствующее максимуму силы межатомного притяжения F m , определяется из условия (df/dx) x=xm = 0. Используя зависимость (1), находим предельное удлинение связи между атомами: x_m = a / b , откуда относительная предельная деформация межатомной связи равна ( x m =Δ r m )

A rm = a

r0     br0

.

Френкель [3] для коэффициента объемного теплового расширения β твердого тела предложил выражение

в =

bk

2ar02B ,

где k – постоянная Больцмана, B – упругий модуль объемного сжатия. Умножив правую часть данного равенства на отношение (3 N A r 0 /3 N A r 0 ), можно представить его в виде

C V

.

к 6 a ) BV

Здесь C V =3 N A kT =3 R – молярная теплоемкость, V = N A r 0³ – молярный объем, N A – число Авогадро, R – газовая постоянная.

Из сравнения соотношения (3) с известным термодинамическим уравнением Грюнайзена в = Y ,.

приходим к следующей микроскопической интерпретации параметра Грюнайзена γ _D :

br

Yd = A

6a

.

Эту формулу (5) можно получить более строго с привлечением квантовой механики [4, 5].

Использование выражения (5) в равенстве (2) приводит к выводу о том, что предельная деформация межатомной связи определяется величиной γ D

A rm =   1

r о ⁶ Y d

.

Параметр Грюнайзена γ D характеризует нелинейность силы межатомного взаимодействия (отклонение от линейной зависимости f ( x ) (рис. 1), и он пропорционален ангармоническому коэффициенту: γ _D ~ b ((5)). Предельная деформация связи (Δ r_m / r ₀) также связана с отклонением силы межатомного взаимодействия f ( x ) от линейной зависимости (рис. 1). Из формулы (2) видно, что чем больше коэффициент ангармоничности b , тем при меньшей деформации связи (Δ r m / r 0 ) происходит переход от линейной упругой к нелинейной неупругой деформации. Поэтому понятно, почему величины γ D и Δ r m / r 0 оказываются взаимосвязанными.

Для уравнения (4) предложены другие способы расчета параметра Грюнайзена γ D . Заслуживает внимания соотношение Беломестных – Теслевой, позволяющее оценку γ D из данных о коэффициенте Пуассона µ [6],

3 ( 1 + ц

.

Y D = Э I Э T

2 к 2 - 3 ц

Примечательно то, что эта зависимость γ D (µ) находится в согласии с уравнением Грюнайзена (4) [6, 7].

Из равенств (6) и (7) следует, что относительная предельная деформация межатомной связи является однозначной функцией коэффициента Пуассона µ

А Г т = ( 2 - 3 Ц )                                             (8)

r 0      ^{9 ( 1} + Ц )

Коэффициент Пуассона у неорганических стекол и аморфных полимеров (табл. 1-4) меняется в узких пределах [8]. У стеклообразных систем одного класса µ≈ const . Поэтому у различных стекол и полимеров относительная предельная деформация межатомной связи оказывается в первом приближении «универсальной постоянной, равной около 0.1 (табл. 1-4),

А r |

—— I ® const « 0.07 - 0.10 . r 0 )

Критическое смещение связанного атома (рис. 1) называется его делокализацией [2]. В неорганических стеклах и их расплавах в качестве кинетической единицы, подвергающейся делокализации, выступает мостиковый атом типа атома кислорода в мостике Si-O-Si [1, 2], ответственный за вязкое течение.

Таблица 1

Калиево-боратные стекла [8]

Стекло	µ	Δ r m / r 0
K 2 O-B 2 O 3
K 2 O, мол.%
1.1	0.292	0.097
2.5	0.293	0.096
3.9	0.293	0.096
8.5	0.293	0.096
13.0	0.295	0.096
18.0	0.301	0.094
22.8	0.295	0.096
28.2	0.288	0.098
33.5	0.303	0.093

Постоянство относительной предельной деформации межатомной связи (9) можно рассматривать как полу-эмпирический критерий элементарного акта процесса размягчения стекол, который (по аналогии с известным правилом плавления Линдемана) можно сформулировать следующим образом: когда амплитуда тепловых колебаний мостикового атома Δ r m достигает определенной доли среднего межатомного расстояния r 0 , возбужденный делокализованный мостиковый атом теряет устойчивость и начинается переход стекло–жидкость. Предполагается, что критическое смещение атома реализуется при температуре размягчения под действием теплового давления при тепловых флуктуациях [1, 9, 10]. С этой точки зрения размягчение стекол обусловлено возникновением колебательной нестабильности атомов в узлах решетки, как и в случае плавления кристаллов [11].

Таблица 2

Сульфатно-фосфатные стекла [8]

Стекло	µ	Δ r m / r 0
NaPO 3	0.294	0.096
NaPO 3 -Na 2 SO 4 Na 2 SO 4 , мол.% 10	0.299	0.094
20	0.292	0.097
30	0.288	0.098
NaPO 3 -K 2 SO 4 K 2 SO 4 , мол.% 10	0.316	0.089
20	0.316	0.089
30	0.313	0.090
0.4NaPO 3 ∙0.6Na 2 SO 4	0.320	0.088

Полагая в первом приближении выполнение закона Гука вплоть до предельной деформации, воспользуемся соотношением [12]

a = E [^-,                                 (10)

y

V r о )

где E – модуль упругости при одноосной деформации, σ у – предел текучести, выше которого наблюдается неупругая деформация стекол.

У силикатных, германатных и ряда других неорганических стекол предел текучести совпадает с их микротвердостью по Виккерсу H V ≈ σ у [12, 13]. При микровдавливании алмазной пирамидки Виккерса на неорганических стеклах образуются пластические микроотпечатки – лунки [13]. При этом микротвердость H V , равную отношению нагрузки на пирамидку к площади отпечатка, можно рассматривать как предел текучести.

Таблица 3

Аморфные органические полимеры [15]

Стекло	µ	Δ r m / r 0
Полиакрилат	0.40	0.063
Поливинилацетат	0.39	0.066
Поливинилхлорид	0.38	0.069
Полистирол	0.37	0.072
Полибутадиен	0.32	0.088
Полиизопрен	0.31	0.091

Таким образом, при σ _у ≈ H_V с помощью равенства (10) можем определить предельную деформацию межатомной связи (Δ r_m / r ₀) как отношение микротвердости к модулю упругости при 20 ^о C (табл. 4):

^X r m = H^- » const » 0.07 - 0.09 , r 0      E

что у силикатных и германатных стекол в первом приближении согласуется с оценкой, следующей из данных о коэффициенте Пуассона (8): (Δrm/r0) ≈ 0.1 (табл. 4). Ранее из других исходных посылок был предложен не- сколько иной вариант расчета (Δrm/r0) из данных о коэффициенте Пуассона [13, 14]:

A rm = (1 - 2 A )

r0     6 (1 + A )

Интересно отметить, что оценка по этой формуле лучше согласуется с отношением H V / E (табл. 4), чем по соотношению (8), хотя при выводе (12) использованы более грубые приближения, чем в случае (8).

Упругие постоянные, микротвердость и предел текучести неорганических стекол

Таблица 4

	µ	E	H V	H V / E	( 1 — 2 A ) 6 ( 1 + A )	( 2 — 3 A ) 9 ( 1 + a )	σ y , 2 кгс/мм2
		кгс/мм2
		Эксперимент			Расчет
					(12)	(8)	(10) и (12)
SiO 2	0.170	7450	692	0.093	0.094	0.142	700
К-8	0.225	7920	578	0.073	0.075	0.120	586
БК-10	0.250	7516	553	0.074	0.067	0.111	505
ТФ-3	0.219	5469	424	0.078	0.077	0.122	420
ТФ-1	0.225	5355	392	0.073	0.075	0.120	395
Na 2 O-SiO 2
Na 2 O, мол.%:
16	0.218	6144	442	0.072	0.077	0.123	473
20	0.235	5756	405	0.070	0.072	0.117	409
33,3	0.255	5993	364	0.061	0.065	0.109	376
Na 2 O-GeO 2
Na 2 O, мол.%:
5	0.226	5042	370	0.073	0.074	0.120	383
20	0.250	6722	450	0.067	0.067	0.111	456
30	0.265	5529	350	0.063	0.062	0.106	349
GeO 2	0.197	4333	360	0.083	0.084	0.131	373

Таким образом, межатомную связь в стеклах можно растянуть до предельного значения как под действием механического напряжения, равного пределу текучести (11), при комнатной температуре 20 ^о C, так и под действием теплового давления (8) при температуре размягчения. При этом относительная предельная деформация связи (Δ r_m / r ₀) у стекол одного класса оказывается практически постоянной величиной, составляющей около (7-10)% от среднего расстояния между атомами. Делокализация мостикового атома (рис. 1) служит молекулярным механизмом пластической деформации стеклообразных твердых тел и процесса их размягчения [10, 12].