Кручение упругого полупространства с многослойным покрытием периодической структуры

Введение. Многослойные покрытия активно используются для создания современных жаропрочных, абразиво- и эрозионностойких покрытий на поверхности элементов газовых и паровых турбин, деталей машин. Разработан ряд технологий, позволяющих создавать слоистые композиции из чередующихся слоёв различных материалов, в которых толщина слоя может составлять менее 100 нм при общем их количестве до нескольких тысяч [1]. Это газотермическое напыление (в частности, вакуумно-плазменное) и различные способы эпитаксиального нанесения (осаждения из газовой или водной среды). В качестве компонентов покрытия могут быть использованы различные металлы и сплавы, а в случае эпитаксии — полимерные материалы.

В работе [2] рассмотрены многослойные покрытия периодической структуры (чередующиеся слои из алюминия и палладия) со сглаженными границами между слоями. На основании экспериментальных результатов показана перспективность использования подобных покрытий для защиты от разрушения при механическом воздействии.

В настоящей работе анализируются механические характеристики контактного взаимодействия непрерывно-неоднородных и многослойных покрытий периодической структуры, возникающие при кручении упругого однородного полупространства с покрытием недеформируемым круглым штампом.

Задача о кручении однородного упругого полупространства круглым штампом впервые была сформулирована и решена в динамической постановке Рейснером и Сагочи [3]. Снеддон [4], с использованием техники интегральных преобразований, свёл данную задачу к решению интегрального уравнения.

В. Д. Грилицкий [5] построил решение задачи о кручении круглым штампом изотропной двухслойной среды и ортотропного упругого слоя в виде степенного ряда от отношения толщины первого слоя к радиусу штампа.

В работе [6] построено решение задачи о кручении для упругого трансверсальноизотропного полупространства с неоднородным по глубине трансверсально-изотропным покрытием. Решение эффективно для всего набора физических и геометрических параметров задачи. Постановка задачи и построение решения. Недеформируемый круглый штамп с плоским основанием жёстко сцеплен с верхней гранью Γ упругого неоднородного полупространства Ω, состоящего из неоднородного по глубине покрытия толщины H и однородного полупространства (подложки). С полупространством связана цилиндрическая система координат r, φ, z; ось z нормальна плоскости Г и проходит через центр штампа, координата r отнесена к радиусу штампа а. Штамп контактирует с полупространством по поверхности z = 0, r < 1. К штампу приложен крутящий момент M , ось которого совпадает с осью z . Под действием этого момента штамп повернётся относительно оси z на угол ε , вызвав деформацию кручения полупространства Ω .

Модуль сдвига полупространства изменяется с глубиной по закону

G ( z )

Gf ( z ) , - H <  z <  0

G = const ,

.Gs,     -да< z <-H где f(z) — непрерывно-дифференцируемая или кусочно-постоянная функция.

Учитывая, что слой подвержен лишь деформации скручивания, ненулевым является лишь смещение вдоль оси φ:

u z = u_r = 0, и ф = и ф ( г , z ) .

Вне штампа плоскость Γ имеют вид:

не нагружена. При сделанных предположениях граничные условия z = 0 :

O z = ^Т rz = ⁰ ,

Т ф z = 0, u ф = ^{r E} ,

r >  1, r <  1.

При r ^ да и z ^ -да напряжения исчезают.

Считаем, что перемещения и напряжения сопрягаются на границе между покрытием (верхний индекс (1)) и подложкой (верхний индекс (2)):

₇          •       т( 1 ) - т< 2 )     //(1 ) - //(2 )

z = - ^H :     ^Тф z = ^Тф Z ,   ^U ф = ^U ф .

Требуется определить закон распределения контактных касательных напряжений под штампом

^Т ф z l z = 0 = ^Т ( ^r ) , ^r <  1.

Используя технику интегральных преобразований, поставленную задачу можно свести к решению следующего интегрального уравнения:

1               да jт(p)pjL(u) J1 (urX-1) J1 (upX-1)dudp = AG(0)re, r < 1,                      (1)

где A = H/a — безразмерный геометрический параметр задачи, характеризующий относительную толщину покрытия; J1 (x) — функция Бесселя 1-го рода; L(u) — трансформанта ядра интегрального уравнения, которая строится численно [6].

С использованием двухстороннего асимптотического метода решения парных интегральных уравнений [7] можно построить приближённое решение задачи в аналитическом виде [6]:

Т ( r ) = 4e g ( 0 )b _w 1 ( 0 ) -= L= ^п I        V1 - r

N

+ Z C i

i = 1

[ sh t ^ i x ;* ) - ^ l j cht A A - ^ t ) tdt )

r V 1 - r ^{2   A r} r V t² - r ²

где постоянные C i определяются из системы линейных алгебраических уравнений:

N

Z Ci X i=1

A i ch ( A i X ¹ ) + B k sh ( A i X ¹ )

B k ² - A i ²

1 + B X ¹

+      ~—7 = 0, k = 1,2, ^ , N ;

L. ( 0 ) B^ 2.....

L N ( U ) — аппроксимация трансформанты ядра интегрального уравнения (1) выражением:

, .   JL1J 2 + A ²

^L N ^(U ) = П ц 2   д2 , ^Ai , ^B i ^{G C} .

i = 1 U + B i

Решение (2) является асимптотически точным при λ → 0 или λ → ∞ [7]. Точность решения для произвольного значения λ зависит от точности аппроксимации трансформанты ядра функцией (3). Алгоритм построения аппроксимаций высокой точности и связь между погрешностями решения и аппроксимации описаны в работе [8].

Далее будем полагать, что функцию f(z) определяющую изменение модуля сдвига в по- крытии, описывает один из следующих законов:

1) ^f1 ( z ) = f 0 + 1 - f y¹ cos ( 2n kz ) ,              2) f l ( z ) = ff + ff cos ( 2n kz ) ,

, s f , Z е Z 3) f 3 ( z ) = { 1, z e[- H ,0 ]/ Z 1 ,

, х 1 1/ f 0 , z е Z 4)    f 4 ( z ) =[ 1,    z e[- H ,0 ]/ Z 1 , -7 1 -1 Г 4 j + 1и 4 j + 3 и! Z =          н ,       н 1 У L 4 k        4 k _

В покрытиях 1—4 мягкие «слои» чередуются с жёсткими (рис. 1). Упругие свойства в покрытиях 1 и 2 меняются непрерывно, в покрытиях 3 и 4 слои имеют чёткую границу. Параметр k соответствует количеству периодов отрезка синусоиды, описывающей покрытия 1 и 2. Покрытия 3 и 4 представляют собой пакет из (2 k + 1) слоя. В покрытиях 1 и 3 (2 и 4) модуль сдвига больше (меньше) либо равен модулю сдвига подложки на всём интервале z е [- H ,0 ] .

01       3.5 0 1/3.5       1

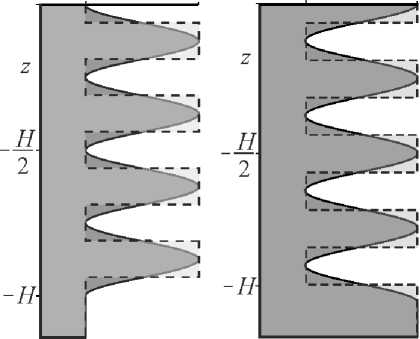
покрытия 1, 3 G(z) покрытия 2, 4

Рис. 1. Графики изменения модуля сдвига по глубине. Сплошные линии соответствуют покрытиям 1 и 2, пунктирные — покрытиям 3 и 4

Показатель неоднородности f ₀ = const >  1 характеризует отношение модуля сдвига на поверхности Г к модулю сдвига подложки. Ограничимся рассмотрением случая f ₀ = 7/2, что соответствует, например, сочетанию мягкого (алюминий, серебро, медь, свинец и т. д.) и жёсткого (железо, сталь, палладий, молибден и т. д.) металлов.

Анализ трансформант ядер интегрального уравнения. На рис. 2 изображены трансформанты ядер для законов 1—4 при k = 1, 10, 50. Из графика видна динамика изменения трансформанты ядра при увеличении числа слоёв.

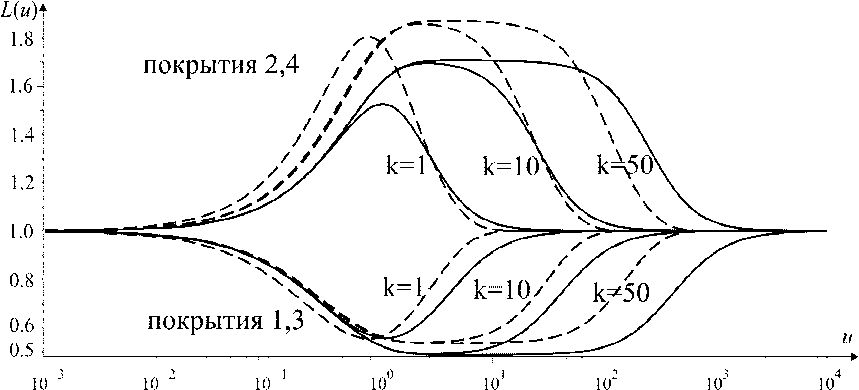
Рис. 2. Трансформанты ядер для законов 1—4 при k = 1, 10, 50. Сплошные линии соответствуют законам 1 и 2, пунктирные — законам 3 и 4

Отметим свойства, общие для слоистых и непрерывно-неоднородных (функциональноградиентных, ФГ) покрытий:

• 1)    трансформанты ядер при всех значениях k имеют одну точку экстремума, обозначим её u 0 . Для законов 2 и 4 — это точка максимума, для законов 1 и 3 — минимума;

• 2)    при увеличении числа слоёв (параметр k ) точка экстремума u 0 сдвигается вправо по оси u ;

• 3)    значение экстремума трансформанты ядра L ( u 0 ) удаляется от 1 (для законов 2 и 4 увеличивается, для законов 1 и 3 — уменьшается) при увеличении k . При этом значения экстремума при k = 10 и k = 50 близки, т. е. можно предположить, что они сходятся к некоторому пределу;

• 4)    при увеличении k расширяется диапазон значений u , в которых значение трансформанты существенно отличается от 1.

Можно заметить ряд качественных отличий трансформант, соответствующих слоистым и ФГ покрытиям:

• 1)    при u < 0,5 трансформанты для законов 1 и 2 практически не изменяются с увеличением параметра k , в то время как графики трансформант ядер для законов 3 и 4 сдвигаются вправо вдоль оси u , приближаясь к некоторому пределу;

• 2)    экстремальные значения трансформант ( L ( u 0 )) для слоистых покрытий, больше, чем для ФГ;

• 3)    для слоистых покрытий L ( u ) стремится к 1 при u → ∞ быстрее, чем для ФГ.

Анализ контактных напряжений. Таблица 1 содержит величины погрешности аппроксимации трансформант ядер выражениями (3) для законов 1—4, где погрешность определяется формулой:

Д L = max L N ( u )/ L ( u ) - 1| • 100 %.

Таблица 1

Погрешность аппроксимации трансформант ядер для законов 1—4

	k = 1	k = 2	k = 4	k = 10	k = 50
закон 1	0,32 %	0,26 %	0,5 %	0,19 %	1,1 %
закон 2	0,53 %	0,58 %	0,47 %	0,19 %	0,52 %
закон 3	0,16 %	0,20 %		0,34 %
закон 4	0,18 %	0,33 %		0,43 %

Из значений таблицы видно, что построены аппроксимации высокой точности для всех рассматриваемых законов и значений параметра k , следовательно, погрешность построенных решений мала.

Введём величину: т re ( Л, r ) = т ( Л, r )/ т hom ( r ) , где т ( Л, r ) — контактные напряжения под штампом для покрытий 1—4; т _hom ( r ) — контактные напряжения, возникающие в однородном полупространстве с модулем сдвига, равным значению модуля сдвига на поверхности покрытий 1—4, то есть G = G (0).

Величина т re, ( Л, r ) наглядно демонстрирует отличие контактных напряжений, возникающих на поверхности неоднородного и однородного полупространств, и, в отличие от т ( Л, r ) , не имеет особенности при r = 1. Из физического смысла поставленной задачи следует, что для покрытий 1—4 выполнено т re, ( Л, r ) ^ 1, при Л ^ 0 или Л ^ та.

На рис. 3 изображена зависимость величины т re, ( Л, r ) для покрытий 1, 2 при к = 1, 2, 10 и покрытий 3, 4 при k = 10 от параметра λ в точке r = 0,5. Численный эксперимент показал, что графики для любого фиксированного r е[ 0..0,99 ] качественно не отличаются от приведённых на рис. 3.

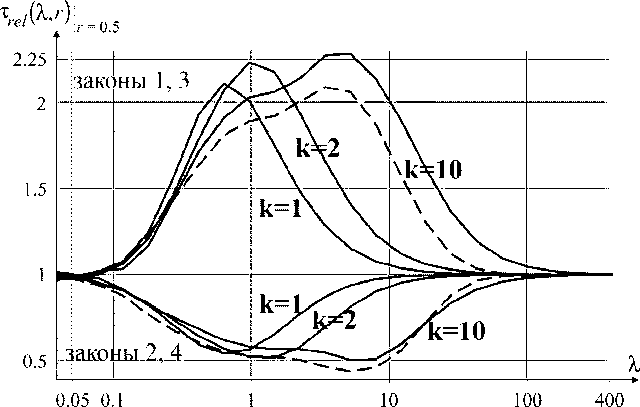
Рис. 3. Зависимость относительных контактных напряжений от параметра λ при r = 0,5

Отметим свойства контактных напряжений для покрытий 1—4, вытекающие из рис. 3:

• 1)    величины т re, ( Л, r ) и т ( Л, r ) при фиксированном r имеет одну точку экстремума (обозначим её λ 0 );

• 2)    при увеличении k точка экстремума λ 0 сдвигается вправо по оси λ. Это означает, что максимальное отличие контактных напряжений для неоднородных покрытий 1—4 и контактных напряжений, возникающих в однородном полупространстве, при увеличении k достигается для всё более толстых покрытий;

• 3)    при увеличении к значение экстремума функции т re, ( Л₀, r ) удаляется от 1 (для закона 2 увеличивается, для закона 1 — уменьшается);

• 4)    при увеличении параметра к расширяется диапазон Л, в котором значение т re, ( Л, r ) существенно отличается от 1 (диапазон λ, где распределение контактных напряжений существенно

отличается от случая однородной среды). Другими словами, неоднородность оказывает существенное влияние на всё более толстые покрытия.

Свойства 1—4 являются общими для слоистых и ФГ покрытий, ниже приведены их основные отличия:

• 5)    экстремальные значения контактных напряжений для слоистых покрытий меньше, чем для ФГ;

• 6)    кривые зависимости контактных напряжений от параметра λ для слоистых и ФГ покрытий похожи, однако, численные значения при фиксированных λ могут существенно отличаться. Например, при k = 10 и λ = 18 отличие контактных напряжений для покрытий 1 и 3 достигает 25 %.

На рисунке 4 изображены графики зависимости величины т re ( Л, r ) от координаты r для покрытия 1, k = 1 при «малых» значениях параметра λ (тонкие покрытия), «средних» λ (покрытия сравнимые с размерами штампа) и «больших» λ (толстые покрытия).

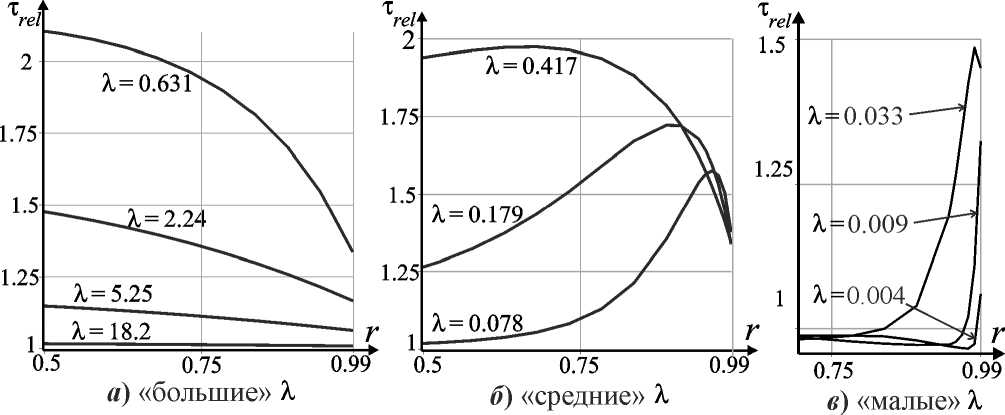
Рис. 4. Относительные контактные напряжения для покрытия 1 при k = 1

Контактные напряжения, возникающие на поверхности покрытия 1 при k = 1, обладают свойствами:

• 7)    контактные напряжения для «больших» значений параметра λ (λ > 1/2) монотонно убывают при r → 1 по сравнению со случаем однородного полупространства. Для λ > 8 разница между т ( Л, r ) и т hom ( Л, r ) менее 8 %, для Л > 25 — менее 1 %;

• 8)    контактные напряжения для «малых» и «средних» значений параметра λ (λ ≤ 1/2) сначала возрастают, а затем убывают при r → 1 по сравнению со случаем однородного полупространства;

• 9)    из рисунка 4 видно, что при уменьшении λ сужаются области возрастания и убывания относительных контактных напряжений по r (см. предыдущее свойство). Контактные напряжения для λ < 0,01 практически не отличаются от случая однородного полупространства везде, кроме окрестности точки r = 1, где наблюдается резкое возрастание, а затем убывание величины относительных контактных напряжений.

Следует отметить, что понятия «больших», «средних» и «малых» значений параметра λ условны, при изменении значения параметра k или рассмотрении покрытий отличных от 1—4 их числовые диапазоны могут существенно измениться.

Свойства, аналогичные 7—9, имеют место и для покрытий 2—4 и всех значений параметра k (изменятся только количественные значения).

В работе произведён анализ контактных напряжений, возникающих на поверхности покрытий. Эта величина представляет наибольший интерес для теоретического исследования, т. к. зная её, легко можно рассчитать всё напряжённо-деформированное состояние полупространства [9].