Квадратурные формулы наивысшей алгебраической степени точности, содержащие наперед заданные узлы

Автор: Хубежты Шалва Соломонович

Журнал: Владикавказский математический журнал @vmj-ru

Статья в выпуске: 1 т.25, 2023 года.

Бесплатный доступ

Приближенные методы вычисления определенных интегралов являются актуальными по сегодняшний день. Среди них самыми популярными оказываются методы квадратур, которые позволяют приближенно вычислить интеграл при помощи конечного числа значений интегрируемой функции. Кроме того, во многих случаях требуются затраты меньшего вычислительного труда, сравнительно с другими методами. С применением многочленов Чебышева первого, второго, третьего и четвертого родов соответственно весовым функциям p(x)=1/√1-x2, p(x)=√1-x2, p(x)=√1+x1-x, p(x)=√1-x1+x, на отрезке [-1,1] строятся квадратурные формулы с наперед заданными узлами a1=-1, a2=1, степени точности 2n+1 c оценками остаточных членов. В этом деле особое место занимает построение ортогональных многочленов по весу p(x)(x2-1) и нахождение их корней. Эта задача оказалась трудоемкой и решались методами вычислительной математики.

Еще

Весовые функции, ортогональные многочлены, квадратурные формулы, наперед заданные узлы, остаточные члены, степени точностей

Короткий адрес: https://sciup.org/143179739

IDR: 143179739 | DOI: 10.46698/l9013-9196-4430-x

Текст научной статьи Квадратурные формулы наивысшей алгебраической степени точности, содержащие наперед заданные узлы

В прикладных задачах математической физики, механики и техники часто возникает необходимость построения таких квадратурных формул, часть узлов которых задается заранее, другая часть узлов может быть взята произвольно [1–3]. Это встречается, например, при решении граничных задач дифференциального уравнения второго порядка на отрезке [a, b].

В таких случаях при выборе квадратурной формулы естественно принять во внимание, что значения неизвестной функции на концах отрезка [a, b] нам известны, и взять формулу вида bn j f (x) dx та Af (a) + Bf (b) + ^ Ak f (xk),

* Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации, соглашение № 075-02-2022-80090.

( 2023 Хубежты Ш. С.

содержащую два фиксированных узла а и b. Прочие узлы x k (к = 1, 2,..., n) являются произвольными.

В общем случае квадратурные формулы, содержащие наперед заданные узлы имеют вид [1]

/ a

p(x)f (x) dx ~ ^ A k f (x k ) + ^ B i f (a i ), (2)

k =1 l =1

в которых m узлов a i , a ₂ > ..., a m фиксированы. Они содержат 2n + m параметров x k , A k (k = 1,..., n) и B i (l = 1,..., m). Попытаемся их выбрать так, чтобы равенство (2) стало точным для многочленов возможно более высокой степени.

Введем два многочлена, связанных с узлами a l и x k :

^(x) = (x — a 1 )(x — a ₂ )... (x — a m ),

w(x) = (x — x 1 )(x — x ₂ )... (x — x n ).

За счет выбора коэффициентов A k и B i формулу (2) можно сделать верной для многочленов степени n + m — 1. Для того чтобы равенство (2) было верным для многочленов степени 2n + m — 1, необходимо и достаточно (см. [1, с. 168]) выполнение следующих условий.

Теорема 1. Для того чтобы формула (2) была точной для многочленов степени 2n + m — 1 , необходимо и достаточно, чтобы

1) она была интерполяционной;
2) многочлен w(x) был ортогонален на отрезке [a, b] по весу p(x)^(x) ко всякому многочлену Q(x) степени ниже n.

Таким образом, построение квадратурных формул (2), верных для многочленов степени 2n + m — 1, приводится к нахождению многочлена w(x) степени n, ортогонального на [a, b] по весу p(x)^(x) ко всякому многочлену меньшей степени. Корни многочлена w(x) должны быть действительными, различными и принадлежать отрезку [a, b]. Кроме того, они должны быть отличны от фиксированных узлов a i (l = 1, 2,... , m). Таким образом, решение этих задач обычным путем представляет большие математические трудности.

В литературе [1, 4, 5] описывается правило построения указанных квадратурных формул. Но конкретные квадратурные формулы, в основном, построены в случаях m = 1, m = 2 и p(x) = 1.

Настоящая заметка посвящена часто встречающимся случаям

^[a,b] = ^[ ^— ¹1], ^m = ^2, p^(x)

p(x) = 1 — x ² ,

p(x) = -

’

p(x)=УШ ■

В этих случаях существуют ортогональные многочлены [1, 6] по указанным весам на отрезке [—1,1]. Их называют многочленами Чебышева соответственно весовым функциям:

I рода, T n (x) = cos(arccos x);

sin(n + 1) arccos x

II рода, U n (x) =------ -----;

1 — x ²

cos —p— arccos x

III рода, C n (x) =----- 2 ----------;

cos 2 arccos x sin + arccosx

IV рода, S n (x) = sin 1 _arccos x

Так как формула (2) является интерполяционной, ее коэффициенты Ak и Bl должны иметь следующие значения:

A k

1 j P^(x)

- 1

w(x)^(x)

(x - X k )w ’ (x k )^(x k ) ^x,

B l

p(x)

- 1

w(x)^(x)

(x - a i )w(a i )^ ' (a i )

dx,

где

^'(xk) = H(xk - xi), ^'(ai) = П(°1 - ai)‘ i=1, i=1, i=k i=1

Для остатка квадратуры R(f ) справедлива формула

^R(f ⁾⁼/

- 1

p(x)П(x)ш ² (x)

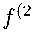
n+m

)(0

(2n + m)

dx,

- 1 < £ < 1.

В [1, с. 173] доказано, что многочлены w(x) при m = 2, ai = -1, a2 = 1 вычисляются по формуле

' = A^x)

P n +2 (x)

P n +1 ( x ) P n ( x )

P _n +2 ( - 1)

P _n +1 ( - 1) P n ( - 1)

P n +2 (1)

P n +1 (1)

P n (1)

где

Q(x) = x ² - 1,

A =

P _n +1 ( - 1)

P n ( - 1)

P n +1 (1)

P n (1)

а P _n (x) — многочлены Чебышева, соответствующие весу p(x) со старшими коэффициентами единицы, т. е. вида P _n (x) = x ⁿ + a i x ⁿ ^- ⁱ + • • • + a _n _- i x + a n .

Будем рассматривать отдельно каждый случай веса p(x).

1. Вычисление интеграла вида : f (x) dx
4. Вычисление интеграла вида

f(x) dx

_-

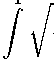
1+x

1 - x ²

- 1

В этом случае формула (2) принимает вид

/ VT - x f ^(x) dx

- 1

Af (-1) + Bf (1) + 52 A k f (x k ), k =1

~ , 1 „ „

^P n ^(x) = 2 n - 1 T n ^(x),

T _n (x) = cos(n arccos x).

После вычисления по формуле (5) получаем

^ш(х) = 2 n U^x)

где U _n (x) =

sin( n +1) arccos x

1 - x ²

— многочлены Чебышева II рода.

Для коэффициентов A, B , A k получены значения

π π π kπ

A = 2(n + 1)^, B = 2(n + 1)^, A k = n+1^, x k = ^COs n+1^,

k = 1, 2,.

Следовательно получается квадратурная формула

/ . . f^(x)dx 2 ^П .f⁽ ^— ^{1) +} 2tnb)f^{(1) + П} .gfx^{) +} R^(f) ⁽⁷⁾

Остаточный член формулы имеет вид

f^nW)

R n ^(f) 2 2n+2 (2n + 2)! ^,

- 1 < £ < 1.

2. Вычисление интеграла вида

j V 1 — x ² f (x) dx

- 1

В этом случае по формуле (5) с подстановкой P _n (x) = 2 n U n (x) для w(x) получается выражение

^W(x) = ₂ n +2 (n ₊I)(x 2 _— 1) ( ⁽n ^{+ 1)U} n +2 ^(x) - ⁽n ^{+ 3)}U n ^(x) ) , ⁽⁸⁾

sin( n +1) arccos x

где U_n (x) = —----- sin ₂ arccos x

Далее для построения квадратурной формулы (2) необходимо знание узлов x _k (k = 1,..., n), т. е. корни многочлена (8). Но они в общем случае не выражаются формулой. Поэтому будем рассматривать частные случаи относительно степени n. Эти случаи при n = 1, 2,..., 6 приведены ниже.

Пусть n = 1. w(x) = x, т. е. корень x i = 0, после вычисления по формуле (3) получаем

A = —, 16,

B = -, A! = 3П,

16^, ¹ 8 ^,

т. е. справедлива формула

[ V ¹ ^— x ² ^f ^(x) dx - ^f ⁽ ^— i) + ^f ⁽¹⁾ + 3^ ^f ⁽⁰⁾.

16 16 8

- 1

Пусть n = 2. По формуле (8) получаем

w(x) = x ² —

x i =-- Tr , 6

^x 2 = ^T ^,6

а по формуле (3) имеем

A= π, B= π, A =9π, A =9π,

40, 40, 1 40, 2 40, т. е. справедлива формула

[ v i - x 2 f (x) dx - П- f ( - 1) + П- f (1) + 9П f f- + 9П f ( Y (io) 40 40 40 6 40 6

- 1

Пусть n = 3. По формуле (3), (8) получаем

ω(x) = x3 - 3 x, x1 = - 3, 88 3 x2 = 0, x3 = 8, A= π, B= π, A =2π, 80, 80, 1 15, A = 5π, A = 2π, 2 24, 3 15, и имеем формулу j v1—x2 f(x) dx - 80 f (-i)+80 f(i)+15 f

- 1

- 3₈

5 π 2 π 3

+₂₄ f (0)+ ₁₅ f ₈

. (11)

Аналогично получается для n = 4. ω ( x ) = x ⁴ -

³ x ² + ³ , A = ^π , B = ^π , 5 ^x ⁺ 80 ^, 140 ^, 140 ^,

узлы x k ( k = 1 , 2 , 3 , 4) и коэффициенты A k ( k = 1 , 2 , 3 , 4) вычисляются приближенно с

точностью ε = 10 ^- ⁸ , и получаем

x 1 = - 0 . 727412

x 2 = - 0 . 266216

x 3 = 0 . 266216

x 4 = 0 . 727412

A 1 = 0 . 261508

A 2 = 0 . 501451

A 3 = 0 . 501451

A 4 = 0 . 261508

n = 5. ω ( x ) = x ⁵

- ⁵ x ³ + ¹ x, A = ^π , B = ^π .

6 ^x ⁺ 8 ^x, 224 ^, 224 ^.

x 1 = - 0 . 798214

x 2 = - 0 . 442930

x 3 = 0 . 000000

x 4 = 0 . 442930

x 5 = 0 . 798214

A 1 = 0 . 172198

A 2 = 0 . 370102

A 3 = 0 . 458149

A 4 = 0 . 370102

A 5 = 0 . 172198

n = 6. ω ( x ) = x ⁶

- ¹⁵ x ⁴ - ¹⁵ x ² - ¹ ,A = ^π ,B = ^π

14 56 112 336 336

x 1 = - 0 . 844751 x 2 = - 0 . 564399 x 3 = - 0 . 198187 x 4 = 0 . 198187

x 5 = 0 . 564399

x 6 = 0 . 844751

A 1 = 0 . 118702

A 2 = 0 . 273839

A 3 = 0 . 383508

A 4 = 0 . 383508

A 5 = 0 . 273839

A 6 = 0 . 118702

Погрешности построенных квадратурных формул равны

R n (f) =

f^)^ j ^ - x (x ² - (x) dx,

— 1 < n < 1.

- 1

3. Вычисление интеграла вида

f (x) dx

В этом случае весовая

, и для отрезка [—1,1] ортогональны- cos arccos x ми являются многочлены Чебышева III рода [4, с. 84], Cn(x) = ----2-------, Pn(x) = cos 2 arccos x

/Cn (x). Многочлен w(x) после вычисления по формуле (5) имеет вид

^w(x) = 2 n +2 ( _n | 1)(x 2 _— 1) ( ^{(n + 1)C} n +2 ^{(x) + C} n +1 ^{(x) (n +} 2^)C n ^(x) ) . ⁽¹²⁾

Корни многочлена w(x) как в случае p(x) = V1 — x2 не выражаются формулой. По этому пришлось рассматривать частные случаи n = 1, 2, 3,4, 5, 6 и вычислить их прибли женно с коэффициентами A, B, Ak (к = 1,..., n). Результаты приведены ниже.

Пусть n =

, / х ^{1 1} „ ^{п 5п} „ ^8п

1. w(x) = x — 4, xi = 4, A =20, B = 12, A1 = 15, и получается формула j УН f dx - 20 f(—1)+5n f <1)+8n f (4) ■

- 1

Пусть n = 2. w(x) =	x 2 _-	1 1 1		' 7	1 + x	/ 7
Пусть n = 2. w(x) =	x 2 _-	3^x 6, ^x ⁱ -"	6	, x 2	^: = 6	^,
A = —, 56 ’	B	- 7n A, ²⁹ '	— 4 V 7_		_A 29 + 4/7 _
A = —, 56 ’	B	= 24’ A ¹ =	84	π,	2	84 "
Пусть n = 3. w(x) =	x 3 _-	3 x 2 — 3 x ₊ 4, 8 8 16 ’	A=	π , 120 ’	B = 9n 40
x i = — 0.537986		A i = 0.339999
x 2 = 0.1528279		A 2 = 0.822336
x 3 = 0.760157		A 3 = 1.246275
Пусть n = 4. w(x) =	x 4 _-	2 о 3 ₂ 3 5 x — 5 x ⁺20	x+	3 80 ’
A = 0.014279		B = 0.575959
x 1 = - 0.682753		A i = 0.190731
x 2 = - 0.161469		A 2 = 0.488488
x 3 = 0.405626		A 3 = 0.812411
x 4 = 0.838596		A 4 = 1.059724
Пусть n = 5. w(x) =	x ⁵ -	- x ⁴ — ⁵ x ³ — 1 12 6 4	x + ~ x — 8		1 64.

A	= 0.008637	B = 0.486199
x 1	= - 0.769541	A 1 = 0.117139
x 2	= - 0.370814	A 2 = 0.309853
x 3	= 0.110027	A 3 = 0.542254
x 4	= 0.562906	A 4 = 0.370102
x 5	= 0.884088	A 5 = 0.916375
Пусть n = 6. ω(x) = x ⁶		3 15 15 - ₇x ⁵ - ₁₄x ⁴ + ₄ x ³ +	15	₂ 3 1
Пусть n = 6. ω(x) = x ⁶		3 15 15 - ₇x ⁵ - ₁₄x ⁴ + ₄ x ³ +	56	x - ₅₆ x - ₁₁₂
A	= 0.008637	B = 0.420749
x 1	= - 0.825326	A 1 = 0.076907
x 2	= - 0.513453	A 2 = 0.207544
x 3	= - 0.114422	A 3 = 0.374688
x 4	= 0.302831	A 4 = 0.549469
x 5	= 0.666169	A 5 = 0.701664
x 6	= 0.912772	A 6 = 0.804959
Для	остаточного члена	справедлива формула 1
	R n (f)	_ f ⁽² ⁿ ⁺²⁾ ( C ) f 1 + x ⁼ (2n + 2)! 1 - x - 1	(x ²	- 1)ω ² (x) dx.

В этом случае p(x) = 11+-xx , и ортогональными являются многочлены Чебышева IV рода (см. [4, с. 84]), Sn(x) = получаем

sin arccos x

² 1 . Тогда P n (x) = ₂ ¹ n S n (x) и по формуле (5)

sin ₂ arccos x

^{ω(x) =} 2 ²⁺ⁿ (n + 1)(x ² -

1) (n + 1)Sn+2(x) - Sn+1(x) - (n + 2)Sn(x) .(13)

Аналогично предыдущему случаю для различных n = 1, 2, 3, 4, 5, 6 получаются значения приведенные ниже.

Пусть n = 1. ω(x) = x + ¹, x 1 = - ¹, A = ^5π, B = ^π , A 1 = ^8π,

4 4 12 2015

1 1 - 1 - ^√ 7 - 1 + ^√ 7

Пусть n = 2. ω(x) = x2 + 3 x - 6 , x1 = 6 , x2 = 6

A = 0.688794 B = 0.056099

x 1 = - 0.607625 A 1 = 1.480401

x 2 = 0.274292 A 2 = 0.688794

Пусть n = 3. ω(x) = x ³ + x ² - x - .

8 8 16

A	= 0.706858	B = 0.026179
x 1	= - 0.760157	A 1 = 1.246279
x 2	= - 0.152829	A 2 = 0.822279
x 3	= 0.537986	A 3 = 0.339999

Пусть n = 4. ω(x) = x ⁴

A = 0.575958

x 1 = - 0.838596

x 2 = - 0.405625

x 3 = 0.161469

x 4 = 0.682753

Пусть n = 5. ω(x) = x ⁵

A = 0.486199

x 1 = - 0.884088

x 2 = - 0.562906

x 3 = - 0.110027

x 4 = 0.370814

x 5 = 0.769541

Пусть n = 6. ω(x) = x ⁶

A = 0.4207493

x 1 = - 0.9127718

x 2 = - 0.6661694

x 3 = - 0.3028313

x 4 = 0.1144215

x 5 = 0.5134534

x 6 = 0.8253261

Для остаточного члена

+²x ³ - ³x ² - ³x+³.

5 5 20 80

B = 0.0142799

A 1 = 1.059724

A 2 = 0.812412

A 3 = 0.488488

A 4 = 0.190731

+ x ⁴ - x ³ - x ² + x + .

12 6 4 8 64

B = 0.008631

A 1 = 0.9163748

A 2 = 0.7611406

A 3 = 0.5422544

A 4 = 0.309853

A 5 = 0.1171396

+³x ⁵ - ¹⁵x ⁴ - ⁵ x ³ + ¹⁵x ² + ³ x

7 14 14 56 56

B = 0.0056099

A 1 = 0.8049599

A 2 = 0.7016636

A 3 = 0.5494689

A 4 = 0.3746883

A 5 = 0.2075442

A 6 = 0.07690723

справедлива формула

^- 112^.

_f (2 n +2) ₍ _ξ ₎

^R ⁿ ^{(f) =} (2n + 2)!

¹1 ^- +^xx^(x ² ^-

- 1

1)ω ² (x) dx, -

1<ξ<1

Все построенные квадратные формулы проверяли на тестовых примерах и получили точные значения интегралов.

Замечание. Квадратурные формулы для интегралов при весовых функциях

1 ^√ 1 - x ²

p(x)

и p(x) = 1 - x2 докладывались на XIV и XV Международных научно- технических конференциях города Пенза в 2020–2021 годах и опубликованы в материа- лах этих конференций [7–8].

Список литературы Квадратурные формулы наивысшей алгебраической степени точности, содержащие наперед заданные узлы

Крылов В. И. Приближенное вычисление интегралов. М.: Наука, 1967. 500 с.
Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. 2-е изд. М.: Физматлит, 2002. 598 с.
Ильин В. П. Численный анализ. Ч. 1. Новосибирск, 2004. 334 c.
Хубежты Ш. С. Квадратурные формулы для сингулярных интегралов и некоторые их применения. Владикавказ: ЮМИ ВНЦ РАН, 2011. 235 с.
Марданов А. А. Вычисление интегралов с особенностями и решение сингулярных интегральных уравнений. Санкт-Петербург: Изд-во Петербург. ун-та, 2017. 104 с.
Пашковский С. Вычислительные применения многочленов и рядов Чебышева. М.: Наука, 1983. 382 c.
Хубежты Ш. С., Нартикоев Н. Б. Квадратурные формулы с наперед заданными узлами с весовой функцией p(x)=1/√1-x2 // Материалы XIV Междунар. науч.-техн. конф. (Пенза, 1-4 декабря, 2020). 2020. С. 22-25.
Хубежты Ш. С., Нартикоев Н. Б. Квадратурные формулы, содержащие наперед заданные узлы с весовой функцией p(x)=√1-x2 // Материалы XV Международной научно-технической конференции (Пенза, 1-4 июня, 2021). 2021. С. 98-102.

Статья научная