Квантовая суперпозиция дискретного спектра состояний математической молекулы корреляции для малых выборок биометрических данных

При проведении экспериментальных исследований далеко не всегда удается получить достаточный объем информации. Например, изучение биологических данных, сопутствующих редким заболеваниям, не может быть обоснова- но в рамках существующих статистических методик. В частности, применение стандартизованной методики проверки статистических гипотез по критерию хи-квадрат1 строится на выборках, состоящих из ≥ 400 опытов. Существуют иные статистические критерии2, менее требовательные к объему тестовой выборки, однако они имеют недостаточно высокую мощность на малых выборках.

Когда речь идет о биологах, изучающих редких животных, или ботаниках, изучающих редкие растения, научная общественность смирилась (де-факто) с отсутствием достаточных объемов статистики по объективным причинам. Для медиков проблема сбора достаточных статистических данных по редким заболеваниям стоит значительно более остро, особенно когда речь идет о редких инфекционных заболеваниях и тестировании новых лекарств.

Еще одной наукой, сталкивающейся с проблемами малых выборок, является биометрия. В период с 1901 г. до конца ХХ в. статистический журнал «Biometrika» (Оксфорд) играл ведущую роль в освещении материала по проблемам малых выборок. В XXI в. биометрия продолжает занимать лидирующее положение по обучению и тестированию преобразователей «Биометрия – код доступа» на малых выборках. При этом объем затрачиваемых средств на биометрию и значимость решаемых биометрией задач ежегодно увеличивается. В США биометрические технологии регулируются ~ 100 национальными стандартами и приблизительно таким же числом международных стандартов. В Российской Федерации было введено 7 национальных биометрических стандартов и адаптировано около 50 международных.

В данной статье отражены последние тенденции развития обработки многомерных биометрических данных, связанные со стремлением решить проблему малых выборок за счет перехода к программной поддержке квантовой суперпозиции при вычислении коэффициентов корреляции.

Обзор литературы

Проблемам малых выборок (обучающих и/или тестовых) в биометрии уделяется значительное внимание в связи с тем, что эти показатели напрямую связаны с эффективностью работы биометрической системы. В США, Канаде, Евросоюзе защита и преобразование биометрических данных осуществляется т. н. «нечеткими экстракторами» [1–3], которые по своим параметрам значительно уступают искусственным нейронным сетям [4]. Применение нейросетевых преобразователей биометрии в код доступа, а также тестирование качества работы нейросетевых преобразователей регламентируются стандартами3-4.

Последний стандарт уникален тем, что он построен на использовании эффектов квантовой суперпозиции при анализе выходных данных искусственной нейронной сети. Именно по этой причине для оценки вероятности ошибок второго рода на уровне 0.000 000 1 стандарт рекомендует использовать всего 32 примера разных биометрических образов «Чужой». Из-за применения новых вычислительных технологий вместо проведения 1 000 000 тестовых опытов достаточно применить всего 32. Мы наблюдаем огромное сокращение объема тестовой выборки и, соответственно, трудозатрат на тестирование из-за отказа от простого статистического перебора в пользу перехода к использованию квантового оракула, предсказывающего вероятности событий по малой выборке.

Следует подчеркнуть, что первоначально квантовая математика разрабатывалась с другой целью. В 1980 г.

• ³    ГОСТ Р 52633-2006. URL: http://www.internet-law.ru/gosts/gost/456

• ⁴    ГОСТ Р 52633.3-2011. Защита информации. Техника защиты информации. Тестирование стойкости средств высоконадежной биометрической защиты к атакам подбора. URL: http://vsegost . com/Catalog/52/2633.shtml

Ю. И. Манин5 первым осознал возможности квантовых вычислительных машин, занимаясь теорией струн. Приблизительно на 50 лет раньше физики столкнулись с тем, что планетарная модель атома «не работает». Бору пришлось вводить гипотезу поглощения и излучения энергии квантами. Позднее задача была формализована в виде уравнения Шредингера, имеющего квантово-волновые решения. Развитие физики и математики привело к тому, что оба направления исследований практически объединились в рамках теории струн6. Фотоны, кварки, фермионы, бозоны, струны на микроуровне (при Платковских длинах) и суперструны на галактическом макроуровне являются квантовым свойством континуума пространства-времени. Многомерные физически существующие пространственно-временные континуумы всегда каким-то образом самоквантуются (сами себя квантуют). Подобные эффекты несомненно могут быть использованы при создании квантовых вычислителей [5] в парадигме Манина-Шредингера или квантово-механических вычислителей.

Ожидаемые огромные скорости вычисления перспективных квантовых компьютеров породили создание ряда важнейших вычислительных алгоритмов, объединение которых позволяет говорить о появлении нового раздела математики – квантовой математики. Важнейшим свойством новой математики является возможность описания связи квантовой энтропии, квантовой суперпозиции и квантовой сцепленности7–8 [6–7] в рамках квантовой информатики.

Непротиворечивое объединение нескольких базовых математических конструкций открыло новые возможности. Когда создавалась квантовая математика, не было другого пути, кроме использования волновых решений уравнения Шредингера и проверки на них новых математических соотношений. После того как элементы квантовой математики были созданы и проверены, использование хорошо изученного уравнения Шредингера стало не обязательным. Объекты, точно соответствующие уравнению Шредингера, очень трудно смоделировать на обычной вычислительной машине8, однако существует множество других уравнений, похожих по создаваемым эффектам.

Одним из аналогов уравнения Шредингера является классический хи-квадрат критерий. Это становится очевидным, если применять его для малых выборок, противореча рекомендациям по стандартизации. Плотность распределения получаемых значений хи-квадрат критерия по мере снижения размеров тестовой выборки становится периодической. Однако если дополнительно выполнить условия синхронизации данных (привязать выбор положения столбцов гистограммы к математическому ожиданию выборки), то положение линий спектра состояний становился таким же стабильным, как положение спектральных линий у молекулы водорода. Таким образом, допустимо рассматривать хи-квадрат критерий как некоторую математическую молекулу [8–11], порождающую стабильный спектр выходных дискретных состояний при квантовании гистограммой некоторого внутреннего континуума непрерывных состояний.

Принципиальное преимущество в данном случае заключается в том, что состояния хи-квадрат молекулы, в отличие от уравнения Шредингера, моделируется всего несколькими строками программного кода. Это означает, что возможно организовать программный квантовый вычислитель, поддерживающий квантовую суперпозицию и квантовую запутанность, соответствующие хи-квадрат молекуле. За счет этого мы можем попытаться значительно усилить мощность хи-квадрат критерия на малых тестовых выборках. Уже созданный вариант такого программного усилителя позволяет за счет учета квантовых эффектов повысить мощность хи-квадрат критерия в 20 раз [11], то есть модифицированный хи-квадрат критерий на выборке из 20 опытов дает такие же вероятности ошибок, как стандартный хи-квадрат при 400 опытах. Предположительно усложнение программы из нескольких строк на языке программирования высокого уровня до нескольких тысяч строк позволит существенно повысить коэффициент усиления мощности критерия [10–11].

Следует отметить, что на молекуле хи-квадрат можно сгенерировать только специализированный вычислитель, усиливающий хи-квадрат критерий. Однако по аналогии с хи-квадрат молекулой возможно построение похожих на нее математических конструкций: эксцесс-молекулы, молекулы асимметрии, молекулы воды и т. д. В рамках данной статьи показывается возможность синтеза математической корреляционной молекулы. Все математические молекулы статистических моментов и критериев остаются узко специализированными вычислителями, поддерживающими эффекты квантовой суперпозиции только для одного статистического функционала на выборке фиксированного объема. Для каждого объема выборки статистические молекулы следует перестраивать (перепрограммировать), поскольку изменяется их спектр.

Для того чтобы сделать универсальный квантовый компьютер с целью решения произвольной задачи, необходимо уметь создавать квантовое обобщение частных квантовых вычислителей. Для этого применяются искусственные нейронные сети9 и естественные нейронные сети [12].

Идея использования искусственных нейронных сетей для распознавания образов спектра разных математических молекул самоочевидна. Хи-квадрат молекула с внутренним континуумом нормальных состояний и хи-квадрат молекула с внутренним равновероятным континуумом состояний имеют разные спектры [10–11]. Достаточно научить одну нейронную сеть распознавать нормальный спектр, а другую нейронную сеть – распознавать спектр молекулы с равномерным внутренним континуумом. Эти две заранее обученные нейронные сети позволят классифицировать спектры любой другой наблюдаемой хи-квадрат молекулы. Каждая нейронная сеть будет решать только свою задачу, оценивая, насколько близок предъявленный спектр тому, чему ее заранее научили.

Отклики двух искусственных нейронных сетей позволяют найти расстояние предъявленного к распознаванию образа до первого базового образа (нормальный спектр) и до второго базового образа (равномерный спектр). Таким образом, вычисляется некото- рая нейросетевая метрика расстояний до двух уже известных спектров базовых образов, например, в пространстве расстояний Хэмминга9.

Следует отметить, что задача обучения искусственных нейронных сетей в ХХ в. и в начале ХХI в. рассматривалась как нетривиальная. Формально это положение сохранялось до принятия ГОСТ Р 52633.5-201110, завершившего 60-летний период эвристического создания множества алгоритмов обучения искусственных нейронных сетей. Алгоритмы, созданные по данной методике, оказались непригодны для быстрого, полностью автоматического обучения больших искусственных нейронных сетей, имеющих несколько сотен входов и 25611 выходов. Абсолютное большинство созданных ранее алгоритмов обучения являются итерационными и потому не могут быть полностью автоматизированы. Кроме того, практически все старые алгоритмы обучения имеют экспонен- циальную вычислительную сложность и, следовательно, непригодны для больших искусственных нейронных сетей.

Алгоритм обучения, принятый в ГОСТ Р 52633.5-2011, построен на создании случайных связей всех входов нейронной сети в целом и входов каждого из нейронов. Для каждого нейрона задается таблица связей путем обращения к программному генератору псевдослучайных целых чисел. Далее производится вычисление весового коэффициента каждого из входов k-го нейрона, исходя из знания математического ожидания входного биометрического параметра E(νi), его стандартного отклонения s(νi), а также знания о требуемом значении отклика нейрона «сk»12 на примере образа «Свой». Формально весовой коэффициент каждого из сети нейронов по данному стандартизованному алгоритму является функцией двух непрерывных переменных и одной дискретной переменной:

0 <  j <  32,

M j,k ( E V ) ^ ( v i ),"c_k ") при <

1 <  i <  416; 2048,

0 < k < 255, где j – номер входа сумматора нейрона; j – номер входа нейронной сети, не превышающие 416 для среды моделирования «БиоНейроАвтограф»13 и 2 048 для рисунка радужной оболочки глаза [3]; переменные индексы j и i связаны между собой заранее заданной таблицей связей Tk(i, j); k – номер нейрона в сети.

Такой алгоритм обучения является абсолютно устойчивым (легко автоматизируется), а его вычислитель- ная сложность становится линейной, т. е. он может быть реализован даже на слабых процессорах мобильных устройств. Несмотря на то, что создание алгоритма обучения ГОСТ Р 52633.5-2011 является итогом почти 60-летних усилий большого количества исследователей, он далеко не идеален. Разработчики биометрических приложений стремятся, с одной стороны, уменьшить размеры обучающей выборки, а с другой стороны – повысить качество решений, принимаемых нейронной сетью. В связи с этим в РФ и Казахстане были инициированы исследования по созданию абсолютно устойчивых алгоритмов обучения больших искусственных нейронных сетей с квадратичной вычислительной сложностью14 [13–19].

Формальная запись алгоритма для перспективного стандарта усложняется незначительно. Перспективный стандарт должен вычислять весовые коэффициенты каждого нейрона по более сложной формуле, дополнительно принимая во внимание коэффициенты корреляции контролируемых нейроном биометрических параметров:

Д у , k ^{( E} ( V I), ° ^V !), r ^V V ),(" c k ") , ⁽²⁾

где m – номер биометрического параметра, по отношению к которому вычисляется корреляция, данный номер должен определяться при обучении и храниться в таблице связей Tk(i, j, m).

Проблема перехода от алгоритмов по ГОСТ Р 52633.5 (1) к перспективным алгоритмам обучения квадратичной сложности по формуле (2) сводится к повышению точности вычисления коэффициентов корреляции на малых выборках:

r ( ν _i , ν _m ) =

1 ∑ n ( E ( ν _i ) - ν _{i , d} ) ⋅ ( E ( ν _m ) - ν _{m , d} ) . (3) n d = 1          σ ( ν _i ) ⋅ σ ( ν _m )

При вычислении коэффициента корреляции происходит накапливание влияния ошибок математических ожиданий ∆ E ( ν _i ) , ∆ E ( ν _m ) и двух стандартных отклонений ∆ σ ( ν _i ) , ∆ σ ( ν _m ) , которые, в свою очередь, зависят от ошибок вычисления математических ожиданий ∆ σ ( ν _i , ∆ E ( ν _i )) , ∆ σ ( ν _m , ∆ E ( ν _m )) .

Таким образом, невозможно точно вычислить коэффициент корреляции на малых выборках. На рис. 1 показано распределение значений коэффициентов корреляции, вычисленных на выборках разного объема.

Из рис. 1 видно, что при выборке из 16 примеров оценка значений независимых данных соответствует коэффициенту корреляции в интервале от –0,7 до +0,7. Если ограничиться значениями, попадающими в интервал от –0,1 до +0,1, то необходимо пропустить порядка 80 % слабо коррелированных параметров. При росте объемов выборки задача вычисления коэффициентов корреляции становится менее сложной, однако невозможно получить большие выборки при обучении преобразователей «Биометрия – код доступа». Пользователи легко идут на предоставление малого количества примеров биометрического образа «Свой». Если требовать от них предъявить большее количество (≤ 21), то пользователи начинают ощущать дискомфорт, рассматривая рост количества примеров в обучающей выборке как ощутимое снижение эргономических качеств их личного средства биометрической аутентификации.

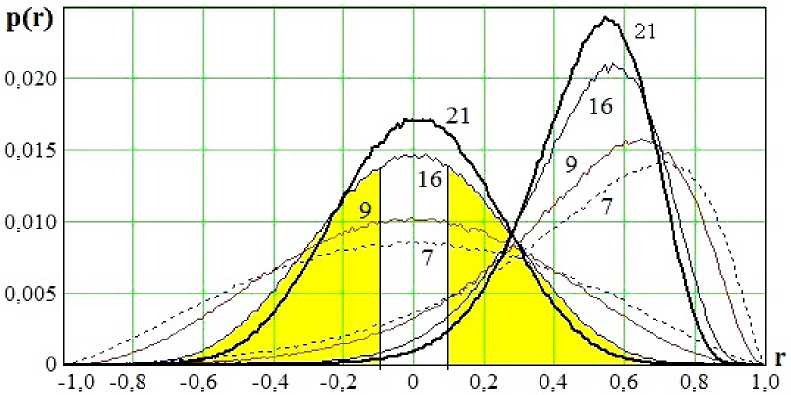
Р и с. 1. Распределение значений коэффициентов корреляции для выборок из n примеров (n = 7, 9, 16, 21) при двух значениях коэффициентов корреляции: r = 0; r = 0,5

F i g. 1. Distributions of values of correlation coefficients for samples from n = 7, 9, 16, 21 examples with two values of correlation coefficients r = 0 and r = 0,5

Методы и материалы

Известно, что центрированные и нормированные независимые данные попадают в круг рассеивания с заданной вероятностью15. При этом для большого количества опытов (N) вероятности попадания в каждую из четвертей круга будут одинаковы:

Данная ситуация отражена на рис. 2.

Для коррелированных данных вероятности попадания в эллиптические сектора (рис. 2) пропорциональны малому и большому диаметрам эллипса:

d P 2 + P 4 n 2 + n 4 D " P , + P 3 ~ n , + n 3 .

P 1

~

n 1 n 2 ~ P) ~ N 2 N

~

P 3

~

n ₃

N

P 4

®

n ₄

N

Подставляя соотношение (6) в известную формулу вычисления коэффициента корреляции15:

где n1, n2, n3, n4 – количество попаданий в первую, вторую, третью и четверную четверти круга соответственно.

В случае, если данные коррелиро-ваны, то соотношение между вероятностями попадания в разные фрагменты эллипса рассеивания изменяется:

r ( x , , x 2 ) =

D — d

D + d

получим формулу для вычисления дискретных значений конечного спектра коэффициентов корреляции:

n1

P 1

n2

> P2  N P4

r ( X 1 , x 2 ) =

P 1 + P 3 - P 2 - P 4

P 1 + P 3 + P 2 + P 4

n 1 + n 3 - n 2 - n 4

n 1 + n 3 + n 2 + n 4

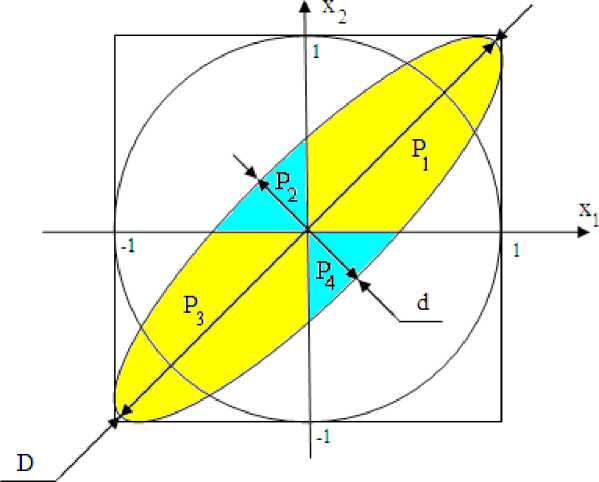
Р и с. 2. Описание центрированных и нормированных площадей рассеивания нормальных данных (независимые данные – круг; зависимые данные – эллипс)

F i g. 2. Description of centered and normalized areas of dispersion of normal data (independent data – circle and dependent data – ellipse)

Таким образом, эллипс распределения зависимых данных является двумерным континуумом корреляционной молекулы, а оси нормированной и центрированной системы координат играют роль двух квантователей, делящих площадь эллипса на четыре части. Получается достаточно простая и понятная математическая конструкция, преобразующая внутренний (не наблюдаемый) двумерный континуум в конечный спектр дискретных выходных состояний. Другими словами, была получена искомая корреляционная молекула, аналогичная хи-квадрат математической молекуле [9–11] или молекуле водорода, состояния которой описываются уравнением Шредингера.

Результаты исследования

Очевидно, что выражение (8) легко может быть воспроизведено программно; более того, два независимых программных генератора псевдослучайных чисел могут быть сцеплены между собой с любым уровнем кор-релированности. Далее можно поддерживать как угодно долго работу такого программного генератора, наблюдая на выходе квантовую суперпозицию 15-и дискретных состояний. На рис. 3 приведены два дискретных выходных спектра состояний корреляционной молекулы и распределение значений ее внутреннего континуального состояния обычных коэффициентов корреляции.

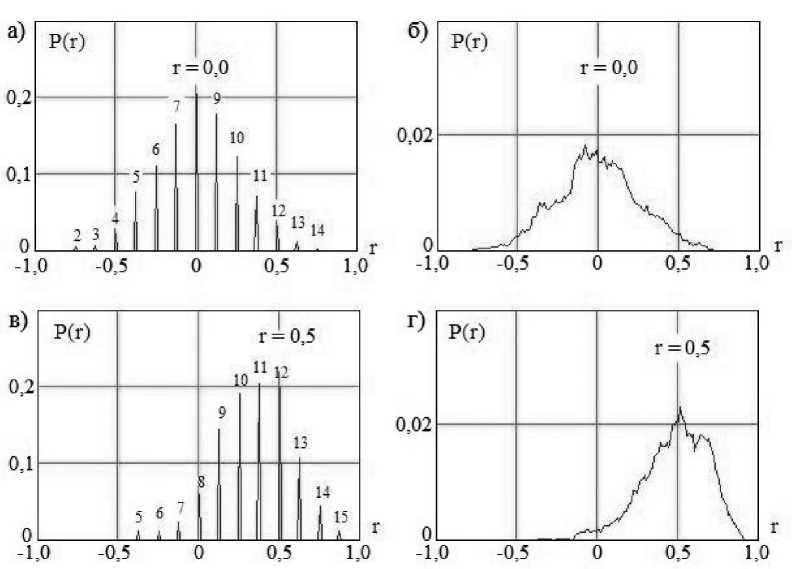
Р и с. 3. Примеры дискретного и непрерывного спектров корреляционной молекулы для двух состояний коррелированности внутреннего программного эмулятора двумерного континуума

F i g. 3. Examples of discrete and continuous spectra of the correlation molecule for two states of correlation of the internal software emulator of a two-dimensional continuum

Из рис. 3 видно, что дискретный спектр выходных состояний корреляционной молекулы для выборок из 16 примеров может иметь до 15 спектральных линий, расположенных по отношению к соседям на расстоянии A r = 0,125. Это позволяет описывать корреляционную молекулу 15-ю членами квантовой суперпозиции:

I ^ = £ V P ( r = - 1 + 0.125 ■ i ) ■ I " bin ( i ) ”), (9) i = 1

где " bin ( i )" – бинарная запись индекса в скобках Дирака длиной в 4 кубита.

Следует обратить внимание на отсутствие в квантовой суперпозиции (9) нулевого члена P ( r = - 1) и последнего

16-го члена P ( r = 1) в силу того, что они полностью детерминированы (бесполезны при расчете квантовой сце-пленности разрядов 4-кубитного квантового вычислителя).

С помощью индуктивного метода можно показать, что для выборок в 32 опыта количество спектральных линий удвоится, а расстояние между ними уменьшится в два раза до A r = 0,0625.

Каждой выборке соответствует определенное количество спектральных составляющих и свое расстояние между ними. На рис. 4 показан дискретный спектр состояний корреляционной молекулы для выборки из 21 примера.

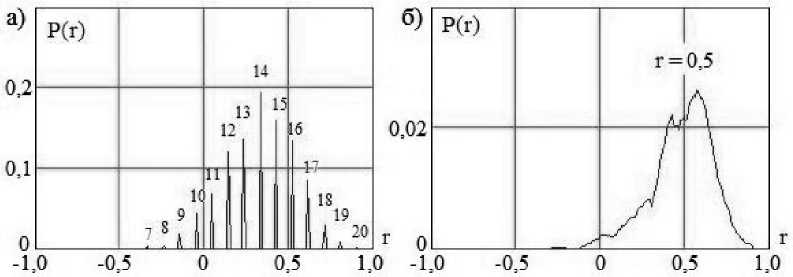
Р и с. 4. Дискретный спектр выходных состояний корреляционной молекулы и его непрерывный аналог для выборки, содержащей 21 пример

F i g. 4 Discrete spectrum of the output states of the correlation molecule and its continuous analog for a sample containing 21 examples

Сравнив рис. 3, в–г с рис. 4, нетрудно убедиться в их подобии. Именно на этом подобии может быть построен циклический континуально-квантовый усилитель мощности корреляционного функционала. Подробнее о принципах создания циклических континуально-квантовых усилителей мощности статистических функционалов можно прочесть в работах [10–11], где подсчитано количество циклов под усилитель хи-квадрат критерия для выборки в 21 пример.

Обсуждение и заключения

Попытки описания конструкций перспективных квантовых компьютеров в квантово-механической парадигме Манина-Шредингера сыграли важную роль в создании новой математической теории, однако в прикладном отношении данная парадигма не вносит существенных изменений. Главным препятствием выступает синхронизация квантово-механических «котов Шредингера». Однако данная проблема исчезает, если отказаться от попыток аппаратной реализации уравнений математической физики, построенных под объект микромира – молекулу водорода. Могут быть использованы куда более простые континуально-квантовые программные уравнения математической хи-квадрат молекулы или математической корреляционной молекулы.

При этом не имеет значения, что формального аналитического описания для континуально-квантовых уравнений, построенных для хи-квадрат молекулы и для корреляционной молекулы, не существует. Для прикладной математики аналитические формализации уравнений и их аналитические решения не нужны. Как показано в данной статье, их квантовая суперпозиция содержит от 15 до 20 значимых компонент. Отметим, что их численное моделирование возможно осуществить на обычном компьютере.

Квантовая суперпозиция и квантовая запутанность для корреляционной математической молекулы могут быть представлены не более чем 20-ю описывающими функциям. Данные функции должны совместно использоваться циклическим континуально-квантовым усилителем мощности корреляционного функционала. Объем кода, реализующий такой усилитель, в настоящее время не определен. Однако есть основания полагать, что объем кодов программного усилителя мощности хи-квадрат критерия (хи-квадрат молекулы) и объем кодов усилителя мощности корреляционного функционала будут сопоставимы. Объем программной реализации квантово-спектрального усилителя мощности корреляционных функционалов предположительно составит до 20 тыс. строк программы на языке высокого уровня. Эта задача не представляет трудностей для группы программистов.