Квантово-химический расчет электронного строения и энергетического спектра ионных кубических кристаллов с дефектами
Автор: Литинский Аркадий Овсеевич, Васильева Галина Юрьевна
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Химическая физика
Статья в выпуске: 11, 2007 года.
Бесплатный доступ
Модель молекулярного кластера в форме расширенной элементарной ячейки и полуэмпирическая расчетная схема MNDO-PM/3 применены к расчету зарядового распределения и энергетического спектра электронов в ионных кубических кристаллах на примере MgO, MgS и CdO с дефектами типа вакансии анион-катионной пары (на поверхности и в объеме), дополнительной ионной пары на поверхности и замещения поверхностного атома металла. Обсуждены особенности состояний, возникающие в спектре идеального кристалла, обусловленные валентными орбиталями атомов дефекта (или примыкающих к ним атомов в случае введения вакансии).
Короткий адрес: https://sciup.org/14968602
IDR: 14968602 | УДК: 539.2:
Текст научной статьи Квантово-химический расчет электронного строения и энергетического спектра ионных кубических кристаллов с дефектами
Модель молекулярного кластера в форме расширенной элементарной ячейки и полу-эмпирическая расчетная схема MNDO-PM/3 применены к расчету зарядового распределения и энергетического спектра электронов в ионных кубических кристаллах на примере MgO, MgS и CdO с дефектами типа вакансии анион-катионной пары (на поверхности и в объеме), дополнительной ионной пары на поверхности и замещения поверхностного атома металла. Обсуждены особенности состояний, возникающие в спектре идеального кристалла, обусловленные валентными орбиталями атомов дефекта (или примыкающих к ним атомов в случае введения вакансии).
Кристаллы типа MgO, MgS и CdO имеют решетку типа хлорида натрия и относятся к ионным кристаллам, для которых характерны узкие валентные зоны и широкие энергетические щели. Их удобно моделировать молекулярным кластером (МК) в виде расширенной (кубической) элементарной ячейки (РЭЯ) [1; 2] без замыкания граничных атомов какими-либо псевдоатомами, поскольку ковалентная составляющая связи в ионных кристаллах мала, а заряды на граничных и внутриобъемных атомах обычно не сильно отличаются друг от друга [3]. Дефекты на поверхности и в объеме кристалла приводят к модификации их энергетического спектра. Настоящая работа посвящена изучению особенностей энергетического спектра электронов, вызванных дефектами в кристаллах MgO, MgS и CdO типа а) вакансии пары атомов (ионной пары); б) дополнительной ионной пары на поверхности; в) замещения атома металла на поверхности.
Модель МК-РЭЯ [4] выбиралась в виде пластины в форме прямоугольного параллелепипеда (6 плоскостей по 32 ионные пары в каждой, всего 384 атома). Модели больших размеров не рассматривались, так как они приводят к значительному росту вычислительных трудностей. В расчетах использовались экспериментальные значения межатомных расстояний R(Mg-O) = 2,1 Å, R(Mg-S) = 2,6 Å, R(Cd-O) = 2,35 Å [5]. При введении дефектов положение соответствующих атомов оптимизировалось. Для расчета электронного строения и энергетического спектра валентных электронов использована полуэмпирическая расчетная схема MNDO-PM/3 [6; 7]. Схемы энергетических зон кубических кристаллов как идеальных, так и содержащих дефекты приведены на рисунке 1.
Уровни электронов, полученные для бездефектных кристаллов (рис. 1а), группируются в зоны занятых состояний (ЗС), преимущественный вклад в которые вносят валентные s- и p-орбитали атомов кислорода или серы (s- и p- ЗС-зоны соответственно), и зону вакантных состояний (ВС), преимущественный вклад в которые вносят валентные орбитали атомов металла. ЗС-и ВС-зоны разделены запрещенными энергетическими щелями (ЗЭЩ). Рассчитанные значения ширин ЗС-зон и энергетических щелей между s- и p-ЗС-зонами (AEg-p) и между верхней границей g-ЗС- и нижней границей ВС-зоны (AEg-c) приведены в таблице 1. Данные этой таблицы свидетельствуют о том, что ширины ЗС-зон малы, а ширины ЗЭЩ велики, что соответствует общепринятым представлениям об ионных кристаллах, причем изменение размера кластера практически не влияет на значения величин AE.
При введении дефектов в спектре одноэлектронных состояний идеального кристалла появляются локализованные состояния, обусловленные орбиталями атомов дефекта, лежащие в окрестности границ энергетических зон как внутри этих зон ( ε с ' , ε v ' , ε ' p , ε s ' ) , так и в области запрещенных энергетических щелей ( ε c " , ε " v , ε " p , ε s " ) (рис. 1). Уровни энергий этих состояний можно охарактеризовать степенями их внедрения 8 в соответствующие зоны или в энергетические щели (в % от ширины соответствующих ЗЭЩ). Рассчитанные величины 8 для всех типов дефектов приведены в таблицах 3, 5, 7. Проанализируем схемы энергетических состояний электронов в зависимости от типа дефекта в ионных кубических кристаллах.
Рис. 1. Схема энергетических уровней электронов ионных кубических кристаллов – идеальных (а) и содержащих дефект (б) (нижние границы s -валентных зон совмещены; зоны заполненных состояний заштрихованы; указаны положения энергетических уровней состояний, обусловленных дефектами)
Таблица 1
Ширины (эВ) энергетических зон и запрещенных энергетических щелей бездефектных кубических кристаллов (обозначения согласно рис. 1)
|
Кристалл |
MgO |
MgS |
CdO |
||||
|
Размер кластера (число атомов) |
8 x 8 x 4 (256) |
8 |
x 8 x 6 (384) |
8 x 8 x 4 (256) |
8 x 8 x 6 (384) |
8 x 8 x 4 (256) |
8 x 8 x 6 (384) |
|
ae : |
32,8 |
38,5 |
17,9 |
21,0 |
14,2 |
15,5 |
|
|
AE V |
6,1 |
6,0 |
6,0 |
6,1 |
5,9 |
6,0 |
|
|
AE gg " c |
9,8 |
9,5 |
5,6 |
5,5 |
6,3 |
6,2 |
|
|
AES g " p |
13,8 |
13,7 |
9,9 |
9,2 |
14,4 |
14,5 |
|
1) Дефекты типа «вакансии» (рис. 2). Рассмотрены три типа таких дефектов, отличающиеся тем, что ионная пара (М, А) удалена: а) с поверхности (ВП); б) с одной и той же плоскости внутри кристалла (ОБ-1); в) атомы М и А удалены из разных соседних плоскостей внутри кристалла (ОБ-2).
Для всех этих случаев в ЗЭЩ возникают состояния ε с " , отделившиеся от нижней границы ВС-зоны. При рассмотрении вакансий в объеме использованы кластеры, содержащие шесть плоскостей (8 х 8 х 6 = 384 атома), для поверхностных дефектов ограничились кластерами из четырех плоскостей (8 х 8 х 4 = 256 атомов). Как следует из таблицы 2, величины зарядов на атомах, соседних с положениями вакансий, убывают в среднем до 10 ^ 12 % для всех типов этого дефекта. Причем значительное снижение зарядов (до 66 %) на соседних атомах имеет место для кристалла MgS. В верхней ЗЭЩ появляются состояния, примыкающие к нижней границе ВС-зоны, обусловленные орбиталями атомов, соседних с вакансиями, с глубиной проникновения 8 " ( s С ) в пределах 3 ^ 32 % (в случае CdO до 57 %). Кроме того, для CdO появляются состояния, преимущественный вклад в которые вносят орбитали соседних с вакансиями атомов, глубоко проникающие вглубь ВС-зоны (от 18 до 39 % от величины A E gP - c ). В верхней ЗЭЩ появляются заполненные состояния, примыкающие к верхней границе ЗС-зоны, для которых 8 " ( s V ) находятся в пределах от 0 до 14 % (в случае CdO и MgS до 42 + 47 %). Для MgS и CdO состояния, обусловленные орбиталями примыкающих к вакансиям атомов, появляются также внутри верхней ЗС-зоны, для которых 8 '( e V ) составляет 4 ^ 10 % (для ВП CdO до 35 %). Исключение составляет случай ОБ-1 для всех типов кристаллов, для которых такие состояния отсутствуют.
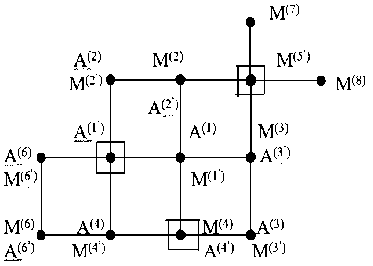
Рис. 2. Обозначение атомов различных плоскостей кубического кристалла М-А и дефектов типа вакансий (М: Mg, Cd; А: O, S):
1, 2, 3,... – атомы в выделенной плоскости; 1 ’ , 2 ’ , 3 ’ , ... и 1 ’’ , 2 ’’ , 3 ’’ ,. .. – атомы из соседних плоскостей (ниже и выше расположенных относительно выделенной плоскости);
дефект типа «вакансии на поверхности» (ВП) – удалены атомы А(5) и М(1) с поверхностной плоскости; объемный дефект (ОБ-1) – удалены атомы А(5) и М(1) с выделенной внутри объема плоскости; объемный дефект (ОБ-2) – удалены атомы М(1) и А(4 ’ ) из соседних внутриобъемных плоскостей
В нижней ЗЭЩ возникают состояния в верхней ее части, степень внедрения которых в ЗЭЩ 8(s p ) находится в пределах 1 + 17 % [для ВП (MgO, MgS), ОБ-2 (MgO) и для ВП и ОБ-2 – дефектов в MgO и MgS такие состояния не образуются]. В нижней части рассматриваемой ЗЭЩ возникают состояния, обусловленные атомами, примыкающими к вакансии, степени внедрения которых 8 ( е Р ) варьируются в пределах 3 ^ 11 % [для ОБ-2 (MgS) и всех типов вакансий CdO состояния ε s " не образуются]. Для ОБ-2 (MgO и MgS) и ВП (CdO) в верхней части валентной s -ЗС-зоны обнаруживаются также состояния ε ' s со степенью внедрения в эту зону 1 ^ 16 %.
Таблица 2
Заряды на атомах различных плоскостей для кубических кристаллов – идеальных и с дефектами типа вакансии (обозначения атомов и типов дефектов приведены на рис. 2)
|
Размер кластера |
8 x 8 x 4 |
8 x 8 x 6 |
||||
|
§ s ^ |
S о н |
Кристалл без дефекта |
Кристалл с дефектом |
Кристалл без дефекта |
Кристалл с дефектом |
|
|
ВП |
ОБ-1 |
ОБ-2 |
||||
|
О |
O (1) |
-0,81 |
-0,66 |
-0,88 |
-0,79 |
-0,79 |
|
O (2) |
-0,81 |
-0,67 |
-0,88 |
-0,76 |
-0,80 |
|
|
М (2) |
0,79 |
0,62 |
0,91 |
0,79 |
0,90 |
|
|
O (3) |
-0,79 |
-0,76 |
-0,86 |
-0,83 |
-0,87 |
|
|
М (3) |
0,78 |
-0,76 |
0,90 |
0,78 |
0,85 |
|
|
O (4) |
-0,80 |
-0,71 |
-0,87 |
-0,78 |
-0,79 |
|
|
М (4) |
0,78 |
0,77 |
0,89 |
0,88 |
0,81 |
|
|
O (5) |
-0,80 |
– |
-0,87 |
– |
-0,86 |
|
|
O (6) |
-0,80 |
-0,71 |
-0,87 |
-0,78 |
-0,78 |
|
|
М (6) |
0,77 |
0,76 |
0,89 |
0,87 |
0,88 |
|
|
М (7) |
0,77 |
0,70 |
0,87 |
0,84 |
0,88 |
|
|
М (8) |
0,75 |
0,67 |
0,89 |
0,81 |
0,88 |
|
|
O (1’) |
-0,78 |
-0,71 |
-0,88 |
-0,79 |
-0,81 |
|
|
O (2’) |
-0,78 |
-0,76 |
-0,88 |
-0,87 |
-0,84 |
|
|
М (2’) |
0,84 |
0,81 |
0,91 |
0,89 |
0,89 |
|
|
O (3’) |
-0,77 |
-0,77 |
-0,87 |
-0,88 |
-0,88 |
|
|
М (3’) |
0,82 |
0,81 |
0,89 |
0,88 |
0,84 |
|
|
O (4’) |
-0,77 |
-0,74 |
-0,87 |
-0,84 |
– |
|
|
М (4’) |
0,83 |
0,80 |
0,89 |
0,88 |
0,81 |
|
|
М (5’) |
0,82 |
0,78 |
0,89 |
0,84 |
0,88 |
|
|
O (6’) |
-0,76 |
-0,74 |
-0,87 |
-0,83 |
-0,84 |
|
|
O (1”) |
– |
– |
-0,82 |
-0,71 |
-0,71 |
|
|
O (2”) |
– |
– |
-0,81 |
-0,82 |
-0,78 |
|
|
М (5”) |
– |
– |
0,87 |
0,80 |
0,86 |
|
|
С/) 5 |
S (1) |
-0,59 |
-0,41 |
-0,57 |
-0,19 |
-0,48 |
|
S (2) |
-0,59 |
-0,44 |
-0,57 |
-0,33 |
-0,47 |
|
|
М (2) |
0,6 |
0,51 |
0,58 |
0,47 |
0,59 |
|
|
S (3) |
-0,59 |
-0,58 |
-0,57 |
-0,50 |
-0,58 |
|
|
М (3) |
0,60 |
0,40 |
0,58 |
0,44 |
0,51 |
|
|
S (4) |
-0,59 |
-0,48 |
-0,57 |
-0,27 |
-0,49 |
|
|
М (4) |
0,60 |
0,63 |
0,58 |
0,39 |
0,53 |
|
|
S (5) |
-0,59 |
– |
-0,57 |
– |
-0,56 |
|
|
S (6) |
-0,59 |
-0,48 |
0,55 |
-0,53 |
-0,48 |
|
|
М (6) |
0,61 |
0,64 |
0,59 |
0,60 |
0,60 |
|
|
М (7) |
0,61 |
0,53 |
0,59 |
0,43 |
0,58 |
|
|
М (8) |
0,57 |
0,47 |
0,55 |
0,52 |
0,55 |
|
|
S (1’) |
-0,55 |
-0,46 |
-0,57 |
-0,53 |
-0,49 |
|
|
S (2’) |
-0,55 |
-0,54 |
-0,57 |
-0,59 |
-0,55 |
|
|
М (2’) |
0,55 |
0,55 |
0,58 |
0,57 |
0,59 |
|
|
S (3’) |
-0,55 |
-0,57 |
-0,57 |
-0,60 |
-0,59 |
|
|
М (3’) |
0,56 |
0,56 |
0,59 |
0,59 |
0,54 |
|
|
S (4’) |
-0,55 |
-0,53 |
-0,57 |
-0,56 |
– |
|
|
М (4’) |
0,55 |
0,55 |
0,58 |
0,58 |
0,53 |
|
|
М (5’) |
0,55 |
0,51 |
0,58 |
0,52 |
0,60 |
|
Окончание таблицы 2
|
Размер кластера |
8 x 8 x 4 |
8 x 8 x 6 |
||||
|
§ S |
S о н |
Кристалл без дефекта |
Кристалл с дефектом |
Кристалл без дефекта |
Кристалл с дефектом |
|
|
ВП |
ОБ-1 |
ОБ-2 |
||||
|
5 |
S (1”) |
– |
– |
-0,55 |
-0,50 |
-0,44 |
|
S (2”) |
– |
– |
-0,55 |
-0,60 |
-0,54 |
|
|
М (5”) |
– |
– |
0,55 |
0,47 |
0,55 |
|
|
о 45 и |
O (1) |
-1,32 |
-1,20 |
-1,31 |
-1,22 |
-1,25 |
|
O (2) |
-1,32 |
-1,15 |
-1,31 |
-1,17 |
-1,25 |
|
|
М (2) |
1,31 |
1,20 |
1,33 |
1,25 |
1,33 |
|
|
O (3) |
-1,32 |
-1,33 |
-1,31 |
-1,32 |
-1,34 |
|
|
М (3) |
1,31 |
1,16 |
1,32 |
1,24 |
1,31 |
|
|
O (4) |
-1,32 |
-0,99 |
-1,31 |
-0,98 |
-0,92 |
|
|
М (4) |
1,31 |
1,33 |
1,32 |
1,33 |
1,25 |
|
|
O (5) |
-1,32 |
– |
-1,31 |
– |
-1,31 |
|
|
O (6) |
-1,32 |
-0,94 |
-1,31 |
-0,91 |
-0,95 |
|
|
М (6) |
1,30 |
1,32 |
1,32 |
1,32 |
1,32 |
|
|
М (7) |
1,30 |
1,19 |
1,32 |
1,25 |
1,33 |
|
|
М (8) |
1,30 |
1,19 |
1,32 |
1,25 |
1,32 |
|
|
O (1’) |
-1,29 |
-1,30 |
-1,31 |
-1,05 |
-1,25 |
|
|
O (2’) |
-1,29 |
-1,32 |
-1,31 |
-1,34 |
-1,31 |
|
|
М (2’) |
1,32 |
1,32 |
1,33 |
1,33 |
1,33 |
|
|
O (3’) |
-1,29 |
-1,32 |
-1,31 |
-1,34 |
-1,34 |
|
|
М (3’) |
1,32 |
1,32 |
1,32 |
1,32 |
1,25 |
|
|
O (4’) |
-1,29 |
-1,30 |
-1,31 |
-1,30 |
– |
|
|
М (4’) |
1,32 |
1,31 |
1,32 |
1,33 |
1,25 |
|
|
М (5’) |
1,32 |
1,25 |
1,32 |
1,25 |
1,32 |
|
|
O (6’) |
-1,29 |
-1,30 |
-1,31 |
-1,32 |
-1,31 |
|
|
O (1”) |
– |
– |
-1,30 |
-1,06 |
-0,95 |
|
|
O (2”) |
– |
– |
-1,30 |
-1,33 |
-1,31 |
|
|
М (5”) |
– |
– |
1,32 |
1,25 |
1,32 |
|
Таблица 3
Степени проникновения δ ’ и δ ’’ (%) состояний ε ’ , ε ’’ , обусловленных дефектами типа вакансии, в соответствующие энергетические зоны (см. рис. 1) и вклады (%, в скобках) орбиталей различных атомов (см. рис. 2) в эти состояния
|
S я 5 н о о и |
MgO |
MgS |
CdO |
||||||
|
Тип дефекта |
Тип дефекта |
Тип дефекта |
|||||||
|
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
|
|
ε c ' , |
δ ′′ =32 М(7)(9) |
δ ′′ =23 М(7)(15) М(8)(20) |
δ ′′ =19 М(3’)(5) |
δ ′′ =26 М(7)(10) М(8)(10) |
δ ′′ =3 М(5’)(14) |
δ ′′ =8 М(4)(12) М (1’) (8) |
δ ′ =41 М(5’)(5) |
δ ′ =146 М(2’)(14) |
δ ′ =145 М(2)(7) М(7)(14) |
|
δ ′′ =26 М(7)(14) |
δ ′′ =19 М (5’’) (13) М (5’) (9) |
δ ′′ =16 М(3’)(14) |
δ ′′ =21 М(7)(7) |
δ ′′ =4 М(5’’)(7) |
δ ′′ =7 М(6)(6) |
δ ′ =99 М(5’)(7) |
δ ′ =139 М(3’)(9) |
δ ′ =138 М(6)(10) |
|
Продолжение таблицы 3
|
S к к 5 н о и |
MgO |
MgS |
CdO |
||||||
|
Тип дефекта |
Тип дефекта |
Тип дефекта |
|||||||
|
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
|
|
ε c |
δ ′′ =25 М(7)(15) М(8)(9) |
δ ′′ =9 М(2)(10) |
δ ′′ =27 М(8)(9) |
δ ′′ =19 М(7)(12) |
δ ′′ =10 М(8)(32) |
δ ′′ =5 М(4)(8) |
δ ′ =52 М(2)(7) |
δ ′ =142 М (4’) (6) |
δ ′ =141 М (6’) (7) |
|
δ ′′ =21 М(8)(7) |
δ ′′ =17 М(7)(19) М(8)(7) |
δ ′′ =11 М(7)(17) М(8)(12) |
δ ′′ =15 М(3’)(6) |
δ ′ =144 М(6’)(12) |
δ ′ =141 М(5’)(11) М(7)(5) |
||||
|
ε c ' , ε c " |
δ ′′ =11 М(7)(6) М(8)(22) |
δ ′′ =12 М (3’) (11) |
δ ′ =37 М(7)(12) |
δ ′ =392 М(2) (94) |
δ ′′ =57 О(2)(15)О (6)(15) |
||||
|
δ ′′ =15 М(7)(30) М(8)(18) |
δ ′ =18 М(8)(5) |
δ ′ =384 М(7) (88) |
δ ′′ =53 О(2)(11), О(6)(11) |
||||||
|
δ ′ =366 М(8)(96) |
δ ′ =95 М(8) (7) |
δ ′ =139 М(8)(12) |
|||||||
|
δ ′′ =35 O(1’)(16) O(4)(19) O(6)(23) |
δ ′ =382 М(8) (96) |
||||||||
|
ε v , ε v ' |
δ ′′ =14 О(6)(58) О(4)(7) |
δ ′′ =0 О(1’)(16) O3(15) O(4)(40) |
δ ′′ =0 O (1”) (9) О(5)(13) О(2)(35) |
δ ′′ =1 S(6)(27) S(4)(14) |
δ ′′ =1 S(1’)(19) S(1)(8) |
δ ′ =10 S (4’’) (9) S(2’’)(7) |
δ ′′ =7 O(2)(14)O (4)(15) |
δ ′′ =1 О(1’)(15) O(4)(7) O(1”)(21) |
δ ′ =7 О(2) (9) |
|
δ ′′ =12 O(4)(14) О(6)(54) |
δ ′′ =2 O3(59) O(4)(11) |
δ ′′ =1 O (1”) (11) О(5)(36) О(2)(22) |
δ ′ =10 S(2)(6) |
δ ′′ =2 S (1’) (5) S(1”)(5) |
δ ′ =10 S(2)(7) S(6)(13) |
δ ′′ =4 О(6)(5) |
δ ′′ =42 О (1’) (16) О(3)(27) O(4)(22) O(1”)(12) |
δ ′ =6 О(6)(8) О(6)(6) |
|
|
δ ′′ =11 О(1’)(10) O(4)(24) О(6)(24) |
δ ′′ =2 О(2)(54) О(5)(17) |
δ ′ =8 S(2)(8) |
δ ′′ =47 S(2)(18) S(4)(7) S(1)(28) |
δ ′ =9 S(4’’)(10) S(2)(8) |
δ ′′ =3 О(6)(16)О (2)(9) |
δ ′ =4 О(6)(7) |
|||
|
δ ′′ =10 O(4)(56) |
δ ′ =1 S(1’)(24) |
δ ′ =8 S(4’’)(6), S(2)(17) |
δ ′′ =2 O (1’) (11) |
||||||
|
δ ′′ =9 О(1’)(53) δ ′′ =7 О(1’)(15), O(4)(28), О(6)(10) δ ′′ =6 O(1’)(50), |
δ ′ =35 O(6) (8) |
||||||||
Окончание таблицы 3
|
(Я к к 5 н о и |
MgO |
MgS |
CdO |
||||||
|
Тип дефекта |
Тип дефекта |
Тип дефекта |
|||||||
|
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
ВП |
ОБ-1 |
ОБ-2 |
|
|
ε " p |
8"=3,5 O(1)(5) |
8"=0,6 S(4)(9) S(1)(5) |
8"=12 М(7)(8) М(8)(8) |
8"=17 М(56)(׳), М(7) (7), M(7”)(7), М(2)(5), М(8)(7) |
δ=15 М(4’)(5), М(1’)(5), М(3’)(7), М(4)(5) |
||||
|
" ε s , ε s ' |
8"=3 O(4)(34), O(1’)(24), O(3)(47) |
8"=6 O(6)(49) |
8 ' =3 O(6) (21) |
8"=11 S(6)(43), S(4)(24), S(2)(7) |
8"=3 S(1’)(14), S(1)(24) |
8 ' =3 S(2)(13), S(6)(12) |
8 ' =16 O(4)(6) O(6)(8) |
||
|
8 ' =2 O(2)(26), O(6)(11) |
8"=9 S(1’)(42) |
8 ' =1 S(6)(35), S(4”)(30) |
8 ' =10 O(2)(11) O(1)(12) |
||||||
|
8"=7 S(1’)(11), S(2)(16), S(4)(21) 8"=5 S(2)(34) |
8 ' =1 S(2)(41), S(6)(6), S(4”)(17) |
||||||||
2) Дефект типа «дополнительная ионная пара (ДИП) на поверхности» (рис. 3а, табл. 4, 5). ДИП формируются под разными углами относительно поверхности кристалла [121° (MgO), 106° (MgS), 180° (CdO)]; катион-анионное расстояние в ней уменьшено по сравнению с кристаллическим на 15 % (MgO), 27 % (MgS), 13 % (CdO); расстояние между анионом (центром адсорбции) и катионом ДИП также меньше кристаллических величин на 12 % (MgO), на 5 % (MgS), на 14 % (CdO); углы между проекцией ДИП на поверхность и выделенным направлением вдоль поверхности (вдоль линии анион – катион) составляют 10° (MgO), 0° (MgS) и 60° (CdO). Эффективные заряды на атомах ДИП не одинаковы, то есть ДИП поляризована за счет переноса части электронной плотности Ар с ДИП на поверхность [0,31 e (MgO); 0,1e (MgS)] или в обратную сторону [0,05e (CdO)]. Перенесенная электронная плотность перераспределяется между атомами, примыкающими к адсорбционному центру, изменяя их в незначительной степени.
В верхней ЗЭЩ возникают состояния, обусловленные орбиталями атомов ДИП, проникающие в ЗЭЩ как со стороны ВС-, так и со стороны ЗС-зон (отщепленные от этих зон ε c " - и ε v " -состояния соответственно). Степени их проникновения в ЗЭЩ находятся в пределах 8 " ® 7 ^ 39 %; 8’V ® 1 ^ 13 %. В случае MgO и CdO в области ВС-зоны появляются обусловленные дефектом состояния со степенями проникновения 8 " ® 6 ^ 30 %.
В нижней ЗЭЩ возникают состояния (кроме CdO), отщепленные от нижней валентной s -зоны, для которых 8 S ~ 4 ^ 6 %. Появляются также состояния в области нижней части валентной р -зоны (кроме MgS), для которых 8 "р ~ 4 ^ 22 %, а также в области верхней части валентной s -зоны (кроме MgS), для которых 8's » 7 ^ 26 %.
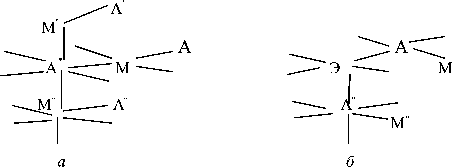
Рис. 3. Обозначения атомов в моделях ионных кристаллов М-А (М: Mg, Cd; A: O, S) с дефектом: а) «ионная пара на поверхности»; б) «замещение атома металла на поверхности»; (Э: Be, Zn, Cd)
Таблица 4
Геометрические параметры и заряды на атомах q в кубических кристаллах М-А с дефектами типа «ионная пара на поверхности»
|
MgO |
MgS |
CdO |
|
|
R(М-А), Å |
2,10 |
2,60 |
2,35 |
|
R(М׳-А*), Å |
1,85 |
2,46 |
2,02 |
|
R(М׳-А׳), Å |
1,73 |
1,88 |
2,04 |
|
α , град |
121 |
105,63 |
180 |
|
β, град |
10 |
0 |
60 |
|
q (М׳) |
0,47 |
0,31 |
0,98 |
|
q (О׳) |
-0,78 |
-0,41 |
-0,93 |
|
q (М) а/б |
0,77/0,83 |
0,60/0,56 |
1,31/1,29 |
|
q (А) а/б |
-0,80/-0,78 |
-0,60/-0,56 |
-1,32/-1,33 |
|
q (А*) а/б |
-0,81/-0,74 |
-0,60/-0,56 |
-1,32/-1,33 |
|
q (М״) а/б |
0,84/0,85 |
0,55/0,58 |
1,32/1,33 |
|
q (А״) а/б |
-0,78/-0,80 |
-0,55/-0,55 |
-1,30/-1,30 |
-
* R(М-А) – межатомные расстояния; α – угол А*М ′ А ′ ; β – угол между плоскостями А ′ М ′ А* и МА*М; а/б – для кристалла идеального и с дефектом соответственно.
Таблица 5
Степени проникновения δ (%) состояний ε ’ , ε ’’ , обусловленных дефектом типа «ионная пара на поверхности», в соответствующие энергетические зоны (см. рис. 1) и вклады (%, в скобках) орбиталей различных атомов (см. рис. 3а) в эти состояния
|
Состояния |
MgO |
MgS |
CdO |
|
ε c |
δ=8 M (6); δ=18 M7) ׳׳); δ=30 M (8) |
δ=6,5 M6) ׳); |
|
|
ε c |
δ=35 M9) ׳׳); δ=32 M35) ׳); δ=32 M28) ׳) |
δ=14 M7) ׳); δ=13M (7); δ=7 M8) ׳) |
δ=19 M19) ׳); δ=19 O25) ׳); δ=39 O18) ׳) |
|
ε v |
δ=1 O50) ׳), O (6); δ=2 O29) ׳), O (5), O9) ׳׳) |
δ=5 S8) ׳), S23) ׳׳) |
δ=13 O* (8); δ=1,6 O (7); δ=1 O8) ׳׳) |
|
' ε v |
δ=18 S* (7); δ=19 S (7); δ=27 S9) ׳) |
δ=42 O82) ׳); δ=23 O* (8) |
|
|
ε ' p |
δ=22 O* (9) |
δ=12 O* (10); δ=11 M5) ׳); δ=4 M5) ׳) |
|
|
ε s |
δ=4 O83) ׳) |
δ=6 S15) ׳) |
|
|
' ε s |
δ=26 O* (13) |
δ=9 O* (12); δ=7 O15) ׳) |
-
3) Дефект типа «замещение поверхностного атома металла» (см. рис. 3б, табл. 6, 7). Внедренный атом оказывается углубленным вглубь кристалла, если его масса меньше массы замещаемого атома (наиболее ярко это проявляется в случае замещения бериллием), в противном случае он удаляется от поверхности кристалла (наименее значительно в случае MgS, в наибольшей степени – в случае MgO). Соответствующим образом удлиняются длины связей внедренного атома с соседними атомами кристаллической поверхности. Заряды на атомах вторых соседей (от атома дефекта) изменяются незначительно (не более чем на 1 %). Что касается атомов ближайших соседей, то величины зарядов на них могут как увеличиваться, так и уменьшаться (в пределах от 5 до 78 %) в зависимости от природы заместителя.
Таблица 6
Межатомные расстояния R(Э-А), смещения Δ R атомов дефекта в направлении, перпендикулярном поверхности, и заряды на атомах в ионных кристаллах идеальных и с дефектами замещения поверхностного атома металла (обозначения атомов согласно рис. 3б;
замещается поверхностный атом М на атом Э;
отрицательным величинам Δ R отвечают смещения вглубь кристалла)
|
Кристалл |
Э |
R(Э-А ״ ), Å |
ΔR, Å |
R(Э-А) Å |
q (Э) |
q (А) |
q (M) |
q (А ״ ) |
q (M ״ ) |
|
MgO |
Mg |
2,10 |
– |
2,10 |
0,77 |
-0,81 |
0,78 |
-0,78 |
0,84 |
|
Be |
1,60 |
-0,51 |
2,165 |
1,03 |
-0,87 |
0,79 |
-0,81 |
0,82 |
|
|
Zn |
2,48 |
0,38 |
2,14 |
0,40 |
-0,73 |
0,79 |
-0,77 |
0,82 |
|
|
Cd |
2,65 |
0,55 |
2,17 |
1,35 |
-0,91 |
0,75 |
-0,82 |
0,82 |
|
|
MgS |
Mg |
2,60 |
– |
2,60 |
0,598 |
-0,59 |
0,60 |
-0,55 |
0,55 |
|
Be |
2,30 |
-0,30 |
2,62 |
1,01 |
-0,68 |
0,60 |
-0,64 |
0,54 |
|
|
Zn |
2,64 |
0,04 |
2,604 |
0,13 |
-0,52 |
0,60 |
-0,45 |
0,55 |
|
|
Cd |
2,70 |
0,10 |
2,602 |
1,299 |
-0,75 |
0,58 |
-0,67 |
0,55 |
|
|
CdO |
Cd |
2,35 |
– |
2,35 |
1,31 |
-1,32 |
1,31 |
-1,29 |
1,32 |
|
Be |
1,62 |
-0,73 |
2,46 |
1,00 |
-1,26 |
1,32 |
-1,16 |
1,31 |
|
|
Mg |
1,84 |
-0,51 |
2,41 |
0,69 |
-1,21 |
1,32 |
-1,11 |
1,32 |
|
|
Zn |
2,00 |
-0,35 |
2,38 |
0,29 |
-1,14 |
1,32 |
-1,05 |
1,32 |
Замещение поверхностного атома кубического кристалла приводит к появлению в верхней ЗЭЩ состояний как е С - , так и е V - типа (вакантных и занятых соответственно), преимущественный вклад в которые вносят орбитали атома-заместителя со степенями внедрения в ЗЭЩ Sc« 2 ^ 16 %, 5 V ~ 3 ^ 8 %. Состояния, обусловленные дефектами, возникают также в ВС-зоне, причем далеко от ее нижней границы ( ^ С ® 46 ^ 154 %).
В верхней валентной зоне в области ее верхней и нижней границ возникают состояния е V - и е ' - типа, для которых S v ® 9 ^ 26 %, 5р ® 5 ^ 20 %. В нижней части ЗЭЩ появляются состояния е " - и es - типа ( 5 p ~ 5 ^ 16 %, 5” , ~ 1 ^ 5 %). В нижней ЗС-зоне появляются состояния в окрестности ее вершины, характеризуемые степенями внедрения 5 s ~ 3 ^ 31 %.
Таблица 7
Степени проникновения δ’ и δ’’ (%) состояний ε’, ε’’, обусловленных дефектами замещения поверхностного атома металла М на атом Э, в соответствующие энергетические зоны (см. рис. 1) и вклады (%, в скобках) орбиталей различных атомов (см. рис. 3б) в эти состояния
|
Состояния |
МgO |
МgS |
CdO |
||||||
|
Дефект замещения |
Дефект замещения |
Дефект замещения |
|||||||
|
Э |
Be |
Zn |
Cd |
Be |
Zn |
Cd |
Be |
Мg |
Zn |
|
' ε c ε c |
δ ′ =4 Э(75) |
δ ′ =2 Э(21) |
δ ′ =0 Э(30) |
δ ′ =1 M(6) |
δ ′ =16 Э(66) |
δ ′ =35 Э(56) |
δ ′ =1 M(58) |
δ ′ =92 Э(32) |
δ ′ =68 Э(27) |
|
δ ′ =4 M(13) |
δ ′ =2 M*(60) |
δ ′ =26 M(7) |
δ ′ =65 Э(87) |
δ ′ =36 Э(66) |
δ ′ =9 M(11) |
δ ′ =23 M(68) |
δ ′ =2 Э(32) |
||
|
δ ′ =4 O ′′ (18) |
δ ′ =1 M(12) |
δ ′′ =16 Э(7) |
δ ′ =77 M(5) |
δ ′ =25 M(5) |
δ ′ =14 M(88) |
||||
|
δ ′′ =14 Э(24) |
δ ′′ =6 M(16) |
δ ′ =19 S ′′ (8) |
δ ′ =16 S ′′ (14) |
||||||
|
δ ′′ =1 O(9) |
δ ′′ =2 M(11) |
||||||||
|
ε v ' ε v |
δ ′′ =8 O(6); |
δ ′′ =7 O ′′ (20) |
δ ′′ =5 O ′′ (21) |
δ ′ =26 S ′ (13) |
δ ′ =12 S ′′ (10) |
δ ′ =4 S ′′ (10) |
δ ′′ =1 O ′ (10) |
δ ′′ =8 O ′ (17) |
δ ′ =3 O ′ (15) |
|
δ ′′ =5 O(6) |
δ ′ =20 O ′′ (10) |
||||||||
|
' ε p " ε p |
δ ′′ =5 O ′′ (13) |
δ ′′ =15 Э(6) |
δ ′′ =15 O ′ (6) |
δ ′ =15 Э(5) |
δ ′ =13 Э(6) |
δ ′ =5 S ′ (27), S ′′ (14) |
δ ′′ =2 Э(8), O ′′ (24) |
δ ′′ =14 O ′′ (10) |
δ ′′ =6 O ′′ (5) |
|
δ ′′ =5 О ′ (6) |
δ ′ =15 S ′′ (8) |
δ ′ =13 S ′′ (9) |
δ ′′ =5 Э(19) |
δ ′′ =24 O ′′ (10) |
|||||
|
" ε s ε s |
δ ′ =10 O(11) |
δ ′ =28 O(9) |
δ ′ =19 O(7) |
δ ′ =20 S(7) |
δ ′ =3 S(6) |
δ ′ =17 S(9) |
δ ′ =0,2 O(17) |
δ ′′ =5 O(19) |
δ ′ =25 O(10) |
|
δ ′ =31 O ′′ (21) |
δ ′ =8 O ′′ (9) |
δ ′ =5 O ′′ (9) |
δ ′ =9 S ′′ (5) |
δ ′ =16 S ′′ (8) |
δ ′ =24 O ′′ (16) |
δ ′ =11 O(13) |
|||
Список литературы Квантово-химический расчет электронного строения и энергетического спектра ионных кубических кристаллов с дефектами
- Эварестов Р.А., Котомин Е.А., Ермошкин А.Н. Молекулярные модели точечных дефектов в широкощелевых твердых телах. Рига: Зинатне, 1983. 287 с.
- Эварестов Р.А. Квантово-химические методы в теории твердого тела. Л.: Изд-во ЛГУ, 1982. 279 с.
- Ермошкин А.Н., Эварестов Р.А. О выборе формы и симметрии кластера в молекулярных моделях кристаллов//Вестн. ЛГУ. 1976. № 10. С. 18-26.
- Лебедев Н.Г., Литинский А.О. Модель ионно-встроенного стехиометрического кластера для расчета электронного строения ионных кристаллов//ФТТ. 1996. Т. 38. Вып. 3. С. 995-962.
- Пенкаля Т. Очерки кристаллохимии. Л.: Химия, 1974. 496 с.
- Stewart J.J.P. Optimization of parameters for semiempirical methods. 1. Methods//J. Comput. Chem. 1989. V.10. № 2. P. 209-220.
- Stewart J.J.P. Optimization of parameters for semiempirical methods. 2. Applications//J. Comput. Chem. 1989. V. 10. № 2. P. 221-264.


