Квантово-химическое моделирование электронных свойств аморфной тетраэдрической структуры

Уникальное сочетание физических свойств аморфных полупроводников относит их к перспективным материалам электронной техники и открывает им пути разнообразного применения. При этом в отличие от затратных технологий выращивания химически чистых полупроводниковых монокристаллов, слабая чувствительность аморфных материалов к примесям позволяет производить их наиболее простыми и экономичными методами, в том числе в виде тонких плёнок обширных площадей на гибких подложках из доступного материала. Среди таких перспективных по-лупроводников своими эксплуатационно-технологическими возможностями особо выделяется аморфный кремний a-Si и его сплавы, в частности a-SiC:H .

Однако промышленному освоению подобных материалов препятствует целый ряд взаимосвязанных научных проблем, ключевой из которых по-прежнему остаётся целенаправленное управление типом и концентрацией носителей заряда в полупроводнике [1], исходное множество которых создаётся в процессе синтеза его вещества. К примеру, аморфный сплав a-SiC:H получают из газовой смеси метана CH 4 и силана SiH 4 плазмохимическим осаждением на ту или иную подложку с одновременным гидрированием растущего материала.

При этом атомная структура конечного вещества, а значит его электропроводность, существенно зависит от пропорций компонентов исходной газовой смеси [2].

Вполне очевидно, что эффективное управление типом и концентрацией носителей заряда в полупроводнике требует отчётливого понимания механизмов квантовых взаимодействий в его атомной структуре и механизмов межатомных и межмолекулярных взаимодействий в процессе его синтеза . Исчерпывающее описание таких механизмов даёт уравнение Шрёдингера и его релятивистский вариант – уравнение Дирака, которые допускают только приближённые решения в рамках зонной теории для твёрдых тел и в рамках молекулярной механики или метода молекулярных орбиталей для химических объектов и процессов. Если при этом математическое описание распределения атомов в кри сталле или молекуле особых затруднений не вызывает, то аналогичная задача для аморфного твёрдого тела традиционно воспринимается как практически неразрешимая научная проблема.

Однако интерпретация аморфной структуры в виде строго закономерного фрактала позволила отыскать эту закономерность в системе итерированных функций, построить предопределённую модель атомной решётки аморфного кремния, подтвердить её адекватность [3, 4, 5] и получить новые возможности теоретического моделирования протекающих в нём электронных процессов. Тем не менее, обретённые возможности моделирования аморфных структур не устраняют необходимость решения уравнения Шрёдингера, а отсутствие периодического потенциала усложняет эту задачу, исключая применение теоремы Блоха и зонной теории. К тому же построенная аморфная структура виртуальна и потому недоступна для экспериментального исследования традиционными техническими средствами. Отсюда возникает проблема практического применения фрактальной модели аморфной атомной структуры.

Поскольку предпосылки эффективного управления типом и концентрацией носителей заряда в полупроводнике создаются в процессе химического синтеза его материала, обращает на себя внимание методология квантовой химии. Аппарат квантовой химии ориентирован на изучение механизмов и энергетики процессов образования и превращений вещества и химических соединений [6], располагает отработанными методами решения уравнения Шрёдингера для молекулярных систем, в том числе лишённых периодического потенциала, и оснащён достаточно мощными программными средствами квантово-химических расчётов, в частности пакетом MOPAC. Отсюда возникает желание применить такой пакет для экспериментального исследования свойств аморфного кремния на фрактальной модели его атомной структуры и формулируется цель выполняемого моделирования – средствами квантово-химического пакета MOPAC выполнить расчёт электронных свойств элементарной ячейки аморфной структуры, рассматривая её как молекулу.

Для выполнения расчёта квантовой системы пакет MOPAC требует описания относительной координации атомов этой системы через её межатомные связи, валентные и диэдрические углы. В нашем случае моделируется тетраэдрическая атомная ячейка аморфного кр емния (рисунок 1), образованная пятью атомами. В формате MOPAC такая структура описывается так называемой внутренней системой координат и называется z-матрицей (таблица 1).

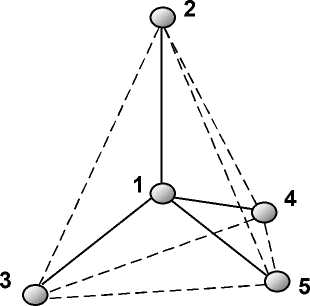
Рисунок 1 - Элементарная тетраэдрическая атомная ячейка

Таблица 1

Внутренняя система координат тетраэдрической атомной ячейки

	1	2	3	4	5	6	7	8	9	10
1	Si	0.00	0	000.0	0	000.0	0	0	0	0
2	Si	2.47	0	000.0	0	000.0	0	1	0	0
3	Si	3.35	0	104.5	0	000.0	0	1	2	0
4	Si	2.75	0	109.1	0	110.0	0	1	2	3
5	Si	3.85	0	110.4	0	140.0	0	1	2	4

6    0

Первый столбец таблицы 1 внутренних координат моделируемой ячейки содержит химические обозначения образующих её атомов. Центральный – первый атом ячейки рисунка 1 целесообразно поместить в начало координат, а остальные атомы естественным образом скоординировать от него через длины межатомных связей, выраженных в ангстремах, валентные и диэдрические углы, выраженные в градусах. В таблице 1 длины межатомных связей даны в колонке 2, валентные углы – в колонке 4, диэдрические углы – в колонке 6. Привязка длин и углов к опорным атомам содержится в колонках 8-10 таблицы 1.

Численные значения внутренних координат получены в результате фрактального моделирования аморфной структуры по авторской методике, изложенной в [3, 4]. Поскольку оптимизация геометрии моделируемой ячейки не планируется, колонки 3, 5 и 7 заполнены нулями.

В среде MOPAC квантово-химические расчёты выполняются полуэмпирическими методами MINDO/3, MNDO, AM1 или PM3. Подробные характеристики этих методов содержат многие литературные источники, например [6, 7, 8]. Откуда следует, что перечисленные методы упрощают решение уравнения Шредингера для атомов и молекул, про- водя расчёты только для валентных электронов с применением стандартных базисных функций и ряда параметров, полученных в эксперименте. При этом методы MINDO/3, MNDO и AM1 последовательно развивают друг друга, а метод PM3 является специализированной версией AM1. В связи с этим запланированные расчёты выполнены методом AM1

в приближении самосогласованного поля (SCF) и при условии общего нулевого заряда моделируемой атомной ячейки.

В соответствии с данными таблицы 1 система MOPAC визуализирует моделируемую атомную структуру (рисунок 2) и производит расчёт её межатомных расстояний (таблица 2).

Таблица 2

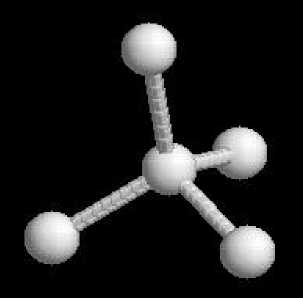
Рисунок 2 - Визуализация моделируемой атомной структуры

Межатомные расстояния

INTERATOMIC DISTANCES

	Si1	Si2	Si3      Si4	Si5
Si	1  .000000
Si	2 2.470000	.000000
Si	3 2.350000	3.811832	.000000
Si	4 2.750000	4.255427	4.008774  .000000
Si	5 2.850000	4.373894	4.078382 4.952998	.000000

Среди остальных результатов с позиций выполняемого исследования наибольший интерес представляют собственные значения (уровни) энергии и коэффициенты молекулярных орбиталей МО (таблица 3), вычисленные атомные заряды и дипольные моменты (таблица 4) и, что особенно ценно, матрица плотности состояний моделируемой атомной структуры (таблица 5). Вывод результатов система завершает краткой сводкой обобщённых сведений (таблица 6).

Таблица 3

Фрагмент массива собственных значений (уровней) энергии и коэффициентов молекулярных орбиталей

ROOT NO. 1				EIGENVECTORS			5 -8.47907	6 -8.20236
				2 -11.03140	3 -10.27681	4 -9.56523
			-12.09927
S	Si	1	-.53397	.06196	.09174	-.34199	.25745	.02898
PX	Si	1	-.11455	.61444	-.06549	.22330	.16165	-.40953
PY	Si	1	-.42771	-.25231	-.14455	.35676	.13299	.22838
PZ	Si	1	.02891	.00561	-.66067	-.22728	-.04354	-.04198
S	Si	2	-.30019	.60895	-.01290	.01102	-.51539	.42085
PX	Si	2	.20256	-.16647	-.02331	.11083	-.40526	.40493
PY	Si	2	-.07346	-.05236	-.03000	.10068	-.04120	.11672
PZ	Si	2	.00539	-.00004	-.10851	-.04394	-.00179	-.01692
S	Si	3	-.51899	-.35186	-.08825	.21318	-.44662	-.44485
PX	Si	3	-.11896	.08500	-.02622	.05795	.11881	.00972
PY	Si	3	.26973	.09085	-.02472	.16243	-.34236	-.41890
PZ	Si	3	.00643	.00494	-.16001	-.06127	-.00614	-.00788
S	Si	4	-.07638	-.05907	.60880	-.34922	-.25714	-.15701
PX	Si	4	-.03111	.05346	.07758	-.01948	.06411	-.02367
PY	Si	4	-.07570	-.04516	.04842	.03587	.01878	.05584
PZ	Si	4	-.06734	-.01222	.12536	-.09712	.10804	.08028
S	Si	5	-.04049	-.04692	-.28331	-.62948	-.19679	-.10070
PX	Si	5	-.02156	.04344	-.04557	-.06188	.04053	-.03430
PY	Si	5	-.05956	-.03933	-.05185	-.00489	.00261	.04106
PZ	Si	5	.04902	.01290	.04573	.13293	-.05459	-.03497

Т а б л и ц а 4

Атомные заряды и дипольные моменты квантовой системы

NET ATOMIC CHARGES AND DIPOLE			CONTRIBUTIONS
ATOM NO	TYPE	CHARGE ATOM	ELECTRON	DENSITY
1	Si	-1.3752	5.3752
2	Si	.4245	3.5755
3	Si	.4531	3.5469
4	Si	.2852	3.7148
5	Si	.2124	3.7876
DIPOLE		X         Y	Z	TOTAL
POINT-CHG	1.	509     2.802	-.784	3.277
HYBRID	-	633    -1.850	.220	1.967
SUM		876       .952	-.564	1.412

Таблица 5

Матрица плотности состояний квантовой системы (фрагмент выходного массива)

0				DENSITY MATRIX IS			S Si2
			S Si1	PX Si1	PY Si1	PZ Si1
S	Si	1	1.090822
PX	Si	1	-.042925	1.423806
PY	Si	1	.007390	.066928	1.349266
PZ	Si	1	.009724	-.021267	-.015680	1.511320
S	Si	2	.194798	.262442	-.073913	.013455	1.833488
PX	Si	2	-.511750	-.654661	.089533	-.019123	.426328
PY	Si	2	-.101249	-.050079	.362596	-.034092	.024659
PZ	Si	2	.013272	-.001625	-.015630	.292500	-.008206
S	Si	3	.206917	-.108567	.262518	.011428	.022449
PX	Si	3	.083741	.245554	.273112	-.007407	-.009384
PY	Si	3	-.541017	.295912	-.539160	-.022071	-.037389
PZ	Si	3	.011763	-.014257	-.008104	.370244	-.002209
S	Si	4	.122154	-.071676	-.114123	-.147239	.006335
PX	Si	4	.151593	.023582	-.144305	-.240985	-.002596
PY	Si	4	.048841	-.014544	.164330	-.141275	.056456
PZ	Si	4	.391280	-.285540	-.324869	-.421083	.032621
S	Si	5	.097460	-.054928	-.095770	.126219	.002297
PX	Si	5	.150541	-.002023	-.147760	.237633	-.002838
PY	Si	5	.035885	-.026394	.147056	.095329	.055333
PZ	Si	5	-.331659	.250280	.273397	-.392721	-.032142

Таблица 6

Краткая сводка основных результатов вычислений

FINAL HEAT OF FORMATION =		60.16607 KCAL
TOTAL ENERGY	=	-398.55513	EV
ELECTRONIC ENERGY	=	-1020.28155	EV
CORE-CORE REPULSION	=	621.72642	EV
IONIZATION POTENTIAL	=	5.56659
NO. OF FILLED LEVELS	=	10
MOLECULAR WEIGHT	=	140.428
COMPUTATION TIME	=	0 h 0 min 1	sec

Таблица 2 показывает отсутствие недопустимо малых величин межатомных расстояний заданной атомной структуры (рисунок 1), что свидетельствует о корректности её исходного описания (таблица 1). Таблица 3 в терминологии MOPAC содержит результаты расчёта молекулярных орбиталей (МО) заданной атомной структуры. Однако, выполняя расчёт элементарной атомной ячейки твёрдого вещества, которая условно рассматривается как молекула, понятие молекулярной орбитали столь же условно уместно заменить понятием орбитали атомной структуры (ОАС) и по-прежнему интерпретировать её как решение уравнения Шрёдингера в тех или иных приближениях. В такой терминологии каждый столбец таблицы 3 соответствует отдельной ОАС.

Программа MOPAC рассчитала квантовую систему в приближениях SCF и ограниченного метода Хартри-Фока (RHF) с десятью дважды занятыми электронами орбиталями, о чём и выдала сообщение « RHF CALCULATION, NO.OF DOUBLY OCCUPIED LEVELS = 10 » и « SCF CALCULATIONS = 2 ». Поэтому таких столбцов в выходном файле всего двадцать, и шесть первых из них показаны в таблице 3. Все ОАС в таблице 3 расположены в порядке увеличения их собственной энергии в эВ или, что равносильно, в порядке увеличения их энергетических уровней. Вычисление ОАС в пакете MOPAC выполнено методом ЛКАО, то есть линейной комбинацией атомных орбиталей (АО), которая в квантовой химии выражается соотношением:

n

ψ _i = ∑ c µ _i ⋅ϕ µ ,              (1)

µ= 1

где ψ _i - искомая ОАС (волновая функция), n

∑ c µ _i ⋅ ϕ µ - линейная комбинация из n ап- µ= 1

проксимирующих АО ϕ µ и c µ _i - весовой коэффициент.

Тогда первое число в каждом столбце таблицы 3 показывает значение собственной энергии соответствующей ОАС в эВ, а последующие числа того же столбца дают значения весовых коэффициентов отдельных аппроксимирующих её АО. В частности, из таблицы 3 следует, что энергия первой орбитали атомной структуры рисунка 1 заданной своими внутренними координатами (таблица 1) составляет -12,09927 эВ, а безразмерные коэф- фициенты аппроксимирующей её АО первого атома кремния равны -0,53397 (1s), -0,11455 (px), -0,42771 (py) и 0,02891 (pz). Аналогичные показатели второй ОАС принимают значения, соответственно, -11,03140 эВ, 0,06196 (1s), 0,61444 (px), -0,25231 (py) и 0,00561 (pz). Таким образом, таблица 3 даёт исчерпывающую информацию о структуре ОАС и вкладе каждого атома в каждую орбиталь моделируемой атомной ячейки. При этом произведение комплексно сопряжённых коэффициентов cµi⋅c*µi определяет вероятность обнаружения электрона на орбитали, а распределение орбиталей по интервалам энергии валентных электронов позволяет вычислить плотность их энергетических состояний – важнейшую характеристику квантовой системы с широким применением в практических расчётах полупроводниковых приборов.

Моделированию электронных свойств отдельной атомной ячейки твёрдого тела, в частности аморфного кремния, средствами квантовой химии нисколько не мешает предположение о нейтральном заряде этой ячейки. Такое предположение логически выделяет элементарную ячейку из общей атомной структуры твердого тела, где она нейтральна, и позволяет применить к ней методологию квантовой химии. Данные таблицы 4 подтверждают нейтральность заряда моделируемой структуры и сообщают её дипольный момент, вычисленный как векторная сумма вкладов всех точечных зарядов атомной ячейки. Такие данные полезны для инженерных расчётов твёрдотельных полупроводниковых приборов и могут быть использованы при разработке технологий изготовления полупроводниковых материалов.

Особый интерес вызывает матрица плотности электронных состояний моделируемой квантовой системы, фрагмент которой содержит таблица 5. Такая матрица исчерпывающе описывает так называемое смешанное состояние квантовой системы – в данном случае элементарной ячейки аморфного кремния (рисунок 1, 2), как статистический ансамбль сразу нескольких квантовых состояний системы. В квантовой механике [9] подобная матрица плотности служит аналогом вероятностно-фазового пространства распределения координат и импульсов частицы в статисти -ческой физике (рисунок 3). Смешанное состояние допускает, что квантовая система с вероятностью p 1 может находиться в состоянии |ψ 1 〉 , с вероятностью p 2 в состоянии |ψ 2 〉 , с вероятностью p 3 в состоянии |ψ 3 〉 и так далее, что и иллюстрирует рисунок 3.

◄----►

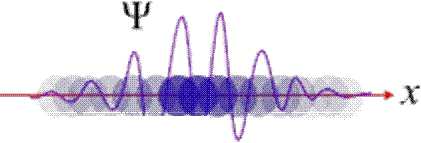
/) = 11

Рисунок 3 - Графическая интерпретация понятия плотности электронных состояний

Для такой системы матрица плотности определяется как оператор:

^р = Z Pi |v i) i|             (2)

i

Тогда содержимое матрицы таблицы 5 составляют возможные электронные состояния |ψ i 〉 и соотнесённые с ними численные значения вероятностей p i обнаружения в этих состояниях электронов квантовой системы рисунка 1.

Практическое значение полученной матрицы (таблица 5) на этом не исчерпывается, а простирается гораздо дальше и повод к такому выводу даёт формальная конструкция | v i Xv i |. Дело в том, что для выполнения запланированного моделирования элементарная атомная ячейка твёрдого тела рассмотрена как изолированная молекула. Однако любое твёрдое тело составляет великое множество подобных ячеек и его свойства создаются всей их структурированной совокупностью в диалектическом отрицании собственных свойств. Поэтому прямой перенос на твёрдое тело результатов количественного расчета его элементарной атомной ячейки и даже их ансамбля, полученных теми или иными методами, неправомерен. Твёрдое тело можно представить как некую большую молекулу. Принципиальных запретов на это нет [10], но размерность такой молекулы порождает непреодолимые технические трудности в её описании и моделировании современными средствами, в том числе квантовой химии. Возникает острое принципиальное противоречие между возможностью и выполнимостью подобного моделирования.

Теперь самое время вновь обратить внимание на конструкцию |^iXvi|, обычно называемую проектором. Символ vi в ней означает i-ю волновую функцию или орбиталь. В нашем случае это орбиталь атомной структуры (ОАС) - аналог молекулярной ор битали (МО) в квантовой химии. Все орбитали моделируемой структуры рисунка 1 вычислены и представлены столбцами матрицы в таблице 3. Если те же орбитали представить не столбцами, а одноимёнными строками vi, то появляется возможность выполнить матричное умножение |viXviI состояний квантовой системы и в итоге получить матрицу плотности, несущую всю информацию о квантовой системе [9]. Для элементарной ячейки аморфного кремния такая матрица реально получена (таблица 5), а поскольку атомами 2, 3, 4 и 5 моделируемая ячейка связана и взаимодействует с атомной структурой, в которую она интегрирована как часть, то через эти взаимодействия на неё проецируются свойства системы в целом. Подобные проекции системных свойств чётко отражаются в матрицах плотности любой части всякой системы, в том числе в матрице плотности любой элементарной атомной ячейки. Таким образом, отпадает необходимость моделирования всей системы целиком, так как все её свойства принципиально выводятся из матрицы плотности любой её части. Технология такого анализа выходит за рамки настоящего исследования и здесь не рассматривается.

Краткая сводка обобщённых сведений о результатах моделирования (таблица 6) включает конечную теплоту образования атомной структуры равную 60,16607 Ккал, общую энергию структуры -398,55513 эВ, суммарную энергию всех её электронов -1020,28155 эВ, энергию межъядерного отталкивания величиной 621,72642 эВ и вычисленный потенциал ионизации 5,56659.

Результаты выполненного моделирования подтверждают возможность и целесообразность применения средств и методов квантовой химии к расчёту электронных свойств локальных атомных структур твёрдого тела. Такую возможность обеспечивает единая методология и математический аппарат квантовой химии и физики твёрдого тела, направленные на изучение межатомных взаимодействий и электронных процессов атомных структур путём решения стационарного уравнения Шрёдингера в одних и тех же приближениях. Квантовая химия, однако, ограничивается моделированием и расчётом отдельных молекул, что в сравнении с атомной структурой твёрдого тела существенно снижает размерность задачи, упрощает и позволяет автоматизировать её решение, не снижая качества получаемых результатов. При этом отсутствие принципи- ального отличия локальной атомной структуры твёрдого тела от молекулы даёт возможность эффективного применения средств и методов квантовой химии к её моделированию и расчёту, а получаемая при этом матрица плотности состояний несёт полную информацию о свойствах всего твёрдого тела.