Квантово-химическое моделирование процессов деформации хиральных углеродных нанотрубок

Введение. В настоящее время одной из самых перспективных и быстроразвивающихся об-(       ).-

,-

( 1      ) [1, 2].

,                                                                                                .,

(                                                                                                   ,-

),

,-

.-

, ,                                                                                                            .-

:-

.                                                                (                                                  ),-

, [3–6].

,,

.

.-

,                                                                                                                                    .-

.

,                                                                                       .                                                                                                                   ,-

–.

Целью настоящей работы является исследование деформированных состояний хиральных

.

Модель. С точки зрения атомистического моделирования углеродные нанотрубки имеют .,

–.

оценке модулей сдвига для моделирования процессов закручивания УНТ более удобна первая

,,

.

.

-

Firefly [7],                                                            ab initio                                 .- нее этот пакет использовался нами при изучении механических свойств зеркальных углеродных нанотрубок [8-10]. Изложенные в работе результаты получены в приближениях Хартри-Фока (предел прочности) и теории функционала электронной плотности (модули Юнга и сдвига). Использовался обменно-корреляционный функционал B3LYP и базисный набор 6-31G.

В данной работе в качестве объектов исследования были выбраны хиральные УНТ с индек-сами хиральности (5,2), (5,3), (6,2), (7,1), (5,4), (6,3), (6,4), (7,3), (6,5), (7,4), (7,6), перечисленными в порядке увеличения диаметра трубок, изменяющегося в пределах от 0,49 до 0,88 нм. Длины исследуемых моделей варьировались от 1,1 до 2,3 нм и ограничивались доступными нам вычислительными ресурсами (кластер Скиф-Аврора, пиковая производительность 117,64 Тфлоп).

.

модулей Юнга и сдвига:

и 2А W E = з Sle1 2А W G = т , Sly2 (1) (2) где AW - изменение полной энергии при деформации растяжения (кручения), S - площадь поперечного сечения нанотрубки, l - длина нанотрубки, е - относительное удлинение, у - угол за крутки .

Алгоритм вычислений механических свойств УНТ состоял в следующем:

• 1)    Проводилась оптимизация геометрии ненапряженной стартовой конфигурации нанотруб

ки , определялась ее полная энергия и координаты атомов.

• 2)    Создавалась напряженная (деформированная) структура.

• 3)    Производилась оптимизация геометрии нескольких напряженных структур с зафиксиро

ванными крайними атомами углерода, которые отличались друг от друга степенью растяжения или закрутки. Для каждой напряженной структуры определялись координаты атомов, полная энергия и ее избыток A W по сравнению с недеформированным состоянием. Результатом вычислений являлась зависимость A W от деформации. Искомые механические характеристики E и G находились подгонкой выражений (1) и (2) под расчетные зависимости A W(e) и AW(Д.

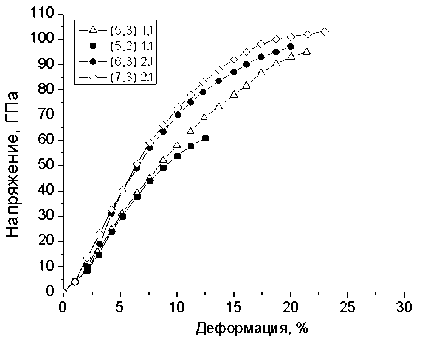
Рис. 1. Зависимости напряжения от деформации для исследованных хиральных нанотрубок

Перед выполнением расчетов механических свойств были сделаны предварительные числен -ные эксперименты методом Хартри-Фока, чтобы выяснить характер зависимости «напряжение-деформация » при растяжении во всем интервале существования нанотрубок. Результаты расчетов для двух «коротких» трубок ((5,2) и (5,3)) длиной l = 1,1 нм и двух «длинных» трубок ((6,3) и (7,3)) длиной 2,1 нм представлены на рис. 1. В этих расчетах на каждом шаге 2) упомянутого выше алгоритма длина трубки увеличивалась на 1 % до тех пор, пока трубка не разрывалась. Предел прочности и предельная деформация нанотрубки соот-ветствуют координатам крайней точки каждой из показанных на рисунке кривых. Видно, что за ис ключением самой тонкой трубки ((5,2)), УНТ имеют примерно одинаковые характеристики при разрыве: предельные деформации около 20 % и предел прочности около 100 ГПа. Для трубки (5,2) эти характеристики составляют 13 % и 61 ТПа соответственно. Возможно, что резкое падение прочностных характеристик есть проявление специфических краевых эффектов, возникаю щих при моделировании деформированных состояний коротких хиральных трубок (см. ниже).

Кривые «напряжение-деформация» имеют выпуклый вид, поэтому область малых деформаций , где эти зависимости еще можно считать линейными, простирается не дальше 5 %. Посколь ку последняя оценка является всего лишь качественной, для контроля во всех приведенных ниже расчетах вычисления проводились в двух различных интервалах деформации растяжения: «умеренных» деформаций (1 < £ < 5 %, шаг Ае = 1 %) и «малых» деформаций (0,1 < £ < 0,5 %, шаг Ае=

Созыкин С .А., Соколова Е.Р.,                    Квантово-химическое моделирование процессов

Тельной К.А., Бескачко В.П., Вяткин Г.П.деформации хиральных углеродных нанотрубок 0,1 %). Выбранные из аналогичных соображений интервалы деформации при кручении составили 0,01 <у< 0,1 рад/нм, шаг Ду = 0,02 рад/нм - для умеренных деформаций и 0,002 <у< 0,01 рад /нм, шаг Ду = 0,002 рад/нм - для малых деформаций. .

возникает вопрос о роли размерных эффектов. На рис. 2 показано, как изменяются модули Юнга изучаемого семейства УНТ в зависимости от длины l рассматриваем ого фрагмента. Из рис. 2, a видно, что при моделировании в режиме умеренных деформаций модули Юнга коротких фрагментов нанотрубок (1,1-1,5 нм) зависят от их индексов хиральности тем сильнее, чем короче трубка. Для l ~ 1 нм различия в величинах E составляют около 40 %, однако какой-либо ясной зависимости E от индексов хиральност и обнаружить не удается. Это связано, скорее всего, со своеобразием краевых эффектов, возникающих при моделировании конечного кластера хиральных трубок. Дело в том, что края хиральных трубок «рваные» в том смысле, что граничные атомы , положения которых при моделировании фиксируются, не укладываются на плоскость, перпендикулярную оси трубки, нарушая осевую симметрию граничных условий и самого деформированного состояния модели. К концу указанного интервала длин (при / - 1,5 нм) разброс значений E заметно уменьшается, а за его пределами (при l ~ 1,6^2,2 нм) этот разброс составляет величину порядка 10 %. Этот результат подтверждается данными, приведенными на рис. 2, б, полученными в режиме малых деформаций. Здесь в интервале l от 1,6 нм до 2,2 нм отличия в модулях Юнга разных нанотрубок также не превышают 10 %, однако значения E всех нанотрубок (кроме трубки (7,6)) монотонно и медленно возрастают с увеличением l . Сравнивая результаты, полученные в режимах умеренных и малых деформаций (рис. 2, а и 2, б), видим, что в последнем режиме оценки для E в целом выше, чем в первом режиме. Скорее всего, это связано с тем, что нелинейная связь между напряжениями и деформациями проявляет себя уже в интервале умеренных деформаций 0:5% (см. рис. 1). Таким образом, при оценке модуля Юнга размерные эффекты, связанные с конечной длиной моделируемого фрагмента УНТ, сильнее всего сказываются для самых коротких из исследованных трубок. Когда их длина превышает 1,6:1,8 нм, эти эффекты если и сказываются, то довольно слабо.

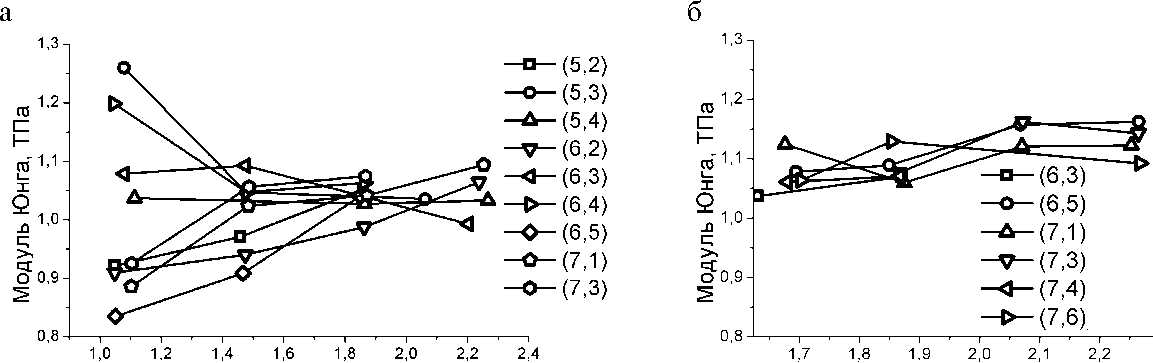
Длина, нм                                             Длина, нм

Рис. 2. Зависимости модулей Юнга хиральных нанотрубок от их длины и диаметра полученные: а) в области «умеренных» деформаций, б) в области «малых» деформаций

Результаты расчетов модулей сдвига G представлены на рис. 3. Как и в рассмотренном выше случае модулей Юнга, модули сдвига, полученные в области «умеренных деформаций» (углов закрутки в данном случае), сильно изменяются в зависимости от длины и индексов хиральности деформируемых нанотрубок (рис. 3, a ). Прозрачная связь между этими индексами и поведением модуля сдвига здесь также отсутствует и по той же, видимо, причине, что и раньше - ввиду потери симметрии в граничных условиях. В области малых деформаций разброс значений модулей сдвига несколько меньше, как и при рассмотрении модулей Юнга (см. рис. 3, б и 2, б). При l > 2 нм величина G слабо зависит от тип а и длины нанотрубки, что позволяет предположить, что G - 0,5 ТПа для всех рассмотренных нанотрубок не слишком малой длины, и, вероятно, для всех достаточно длинных нанотрубок вообще.

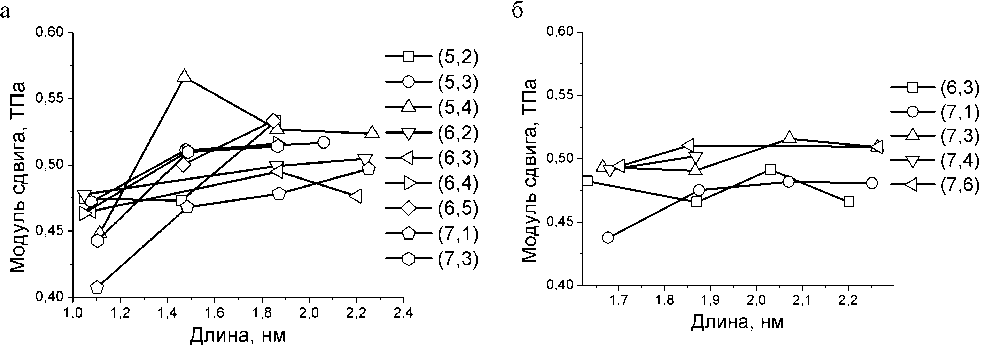
Рис. 3. Зависимости модулей сдвига хиральных нанотрубок от их длины и диаметра полученные: а) в области «умеренных» деформаций, б) в области малых деформаций

,                                                    ,-

«         » «-

».                                                                            (5,2)   (6,2),,

,                                                                                                                                                             ,-

,.

,                                                                                                 ,-

–-

,                                    ,.

серия расчетов механических характеристик УНТ в режиме малых деформаций с использованием

PM3.,

,5%.

, PM3 -

20–25 %.

.,.

• 1.                                                              1,04 – 1,16     .-

• ,>

• 1,6.

• 2.                            G                                              0,5-

• .

• 3.                                                                                       «»

«».