Квантово-механический подход к описанию возможности усиления излучения с помощью континуума нанотрубок

2meR где Uo = const, W - энергия, те - масса электрона.

Воспользуемся аналогичной моделью для описания процесса усиления излучения с помощью удлиненных нанотрубок. В данной работе на основе квантового подхода покажем возможность накачки среды, состоящей из нанотрубок. Накачку среды можно производить нестационарным электрическим полем, перпендикулярным к оси симметрии нанотрубки. Задачу будем решать на основе теории свободных электронов и модели независимых электронов. На основе системы материальных уравнений процесс усиления электромагнитного излучения математически промоделируем.

Нанотрубки представляют собой цилиндрические молекулы с нанометровым диаметром и нанометровой длиной [3-5]. Такое необычное сочетание масштабов длины и диаметра приводит к уникальным свойствам нанотрубок, одним из которых является возможность генерации СВЧ-излучения [6, 7]. Приступим к рассмотрению сформулированной задачи.

О возможности накачки среды с помощью нанотрубок нестационарным электрическим полем. При наличии оператора возмущения ¥^ (наличие нестационарного электрического поля) в цилиндрической системе координат получим

ЭТ й2 52           -        -

+            E = -e^0cos^,              (2)

tit    2meR dtp где Eo - нестационарное электрическое поле, которое направлено перпендикулярно оси нанотрубки; R - радиус нанотрубки. В данной задаче волновая функция одночастичных стационарных состояний, в которых может находиться каждая из частиц, кроме магнитного квантового числа т, будет характеризоваться квантовым числом п за счет квантования в продольном направлении. При этом плотность энергетических уровней Wn за счет большой протяженности по сравнению с поперечными размерами нанотрубок будет значительно больше плотности энергетических уровней Wm. Для проведения оценок предположим, что переход из возбужденного состояния в невозбужденное осуществляется за счет изменения числа частиц в состояниях Тл m, Тл т+1, где волновая функция Тл ш = ^„(^^„(z).

Из уравнения (2) при отсутствии оператора возмущения полной системой ортогональных и нормированных одночастичных волновых функций будут функции:

cos(_W)        h²m²

Ал        2meR где т = 1,2,3.... При т = 0 имеем То = л/2.

Для проведения дальнейших оценок определим приближенно собственную функцию и собственное значение энергии в момент времени Z —> оо для оператора возмущения в формуле (2) при выполнении условия MA = W_m -W_m__x ~|^_т__1от|. Для этого представим решение в виде линейной комбинации Т_т и , в результате в базисе двух собственных функций получим задачу на собственные значения энергии и собственные функции при наличии стационарного возмущения (задача может быть обобщена на случай большего числа собственных функций):

Ч^ССЧ^ + кЧ^-д, W_u=W^p, ^C^-rX), W^W-p. (4)

V                 l                      2

M , vm_x>m= ^*т_\^таф,(5)

/zQ/2 + p \            1       1 /о где C = const.

Если предположить, что стационарное возмущение V в точке z = 0 «мгновенно» включается при t = 0, то из нестационарного уравнения Шредингера (2) с учетом соотношений (4) и (5) получим

W) = АЧ*_П expH^t Ih-iptlh^* ВЧ¹, exp(-iWt lh + iptlh).            (6)

С учетом выражения (6) решение окончательно запишется в виде

T(z) = [{ (А - к B^_m + (5 + кАу¥_т__х } cos( Д/ / Й) -

-i^-B + KA^^ + (A + KB)4^,_m^s"m(Pt/h^exp(-i             (7)

В соответствии с формулами (2) и (3) матричный элемент при т * 1 равен V_m__{x т} = -eRE₀ /2.

Предполагая, что при Z = 0 вероятность распределения удовлетворяет распределению Больцмана, получим (Л - к В^В + кА)^ = ехр(-2р/(kip = а².

Прит = 40. А = НГ⁸т, Е_о = 3■ 10⁶ В/м получим ЙО«3,1-10~²eV; |Е_от__1п;| = 1,5-10"²eV ; ^«2,blO"²eV; K--0.42; a«0,5; Э«1,16В.

Следует отметить, что использование в качестве базисных функций только двух функций оправдано тем, что вероятность нахождения электрона в возбужденном состоянии при MA = W_m -W_m__x ~^_т__х ,„| в соответствии с распределением Больцмана при увеличении т быстро убывает. Для увеличения точности оценок можно было бы использовать три состояния W , W W г т-\'> т’ 'т+1 •

Из полученных оценок следует, что вероятность р|² нахождения электрона в возбужденном состоянии W₊ больше вероятности |Т?|² электрона в состоянии ИД. Это означает, что рассматриваемая система оказывается возбужденной (накаченной ([3]) с величиной накачки V = XZ₀(|y4j² — |s|²), где К- концентрация наночастиц, Z_o - число свободных электронов, которые находятся в возбужденном состоянии (величина будет определена ниже).

Оценка коэффициента усиления в резонаторе. Из полученных выше результатов следует, что если в активной среде, состоящей из множества нанотрубок с определенной ориентацией (ось симметрии наночастицы перпендикулярна направлению нестационарного поля), будет происходить усиление излучения с частотой аж2р1Н. Аналогичное усиление будет происходить и в резонаторе. Оценим коэффициент усиления в резонаторе.

В случае резонатора процесс усиления будет описываться с помощью уравнения для излучения E_z и системы двух материальных уравнений для поляризации Р_ и величины населенности

N ([8], с. 111)

dt 2т_с 2е£₀

dN — +

St

^^^цёр'-рё^

Е h

— + (—-i(Q-co)}p = ^^lL^ at (r₂ J 3h

где o = 2f3/h: щ^- соответственно электрическая проницаемость и электрическая постоянная; в уравнениях (8) в отличие от монографии [8] наличествует связь между индукцией и поляризацией D_z = ee₀E_z + P_z.^ уравнениях (8) введены обозначения (волновая функция Т введена формулой (6))

_ 2 п dUi = \w^-eRcoW^ndy = --^^-.              (9)

л                                     14- К-2   2

Энергия одноуровневых состояний электрона (для m см. (3)), соответствующих стационар ным состояниям одного электрона, в плоскости квантовых чисел n, m удовлетворяют условию

W или

(2лК)² ^ ^ ^ ^ 2m_e Ц² (2я-Л)²,

= W т max

Из соотношения (10) следует, что число энергетических уровней равно M_x=LRm_eW_maxK^h²y Пусть расстояние между центрами атомов в нанотрубке R^ «1,44-Ю”¹⁰ш . Тогда число атомов будет порядка М₂ «2лРЫ R^. Поскольку число атомов равно числу свободных электронов, а число заполненных энергетических уровней в соответствии с принципом Паули примерно в два раза меньше свободных электронов, то получим 1Г_тах « 8тг1Г₀, Иф = Й² !{2m_eR^) «1,7eV. Рассмотрим уровни с m = m_o=4O. В этом случае АИф, -W_m -W_m__x = ^²m_o/(m_eT?²)«O,O3eV, где R = W^S т (при этом максимальные значения квантовых чисел при L = 1 0^-7 т в соответствии с условием (10) будут 1 /              2                                                                                                    -2

n_max = -^\2m_eW_maxL I « 570, m_max «315). При объемной доле наночастиц с₀ =10 концентрация наночастиц будет равна К = с₀ ЦлР²Е) « 3 • 10¹⁹.

Тогда при Z₀=2 инверсия населенностей V = Л2₀^|²-|7?|²) = 8,82-10¹⁹м”³. В рассматриваемой задаче в уравнениях (8) будет иметь место условие P_z"» PJT₂. Поэтому в уравнениях (8) при 69 = 0 в левой части для уравнения поляризации можно пренебречь слагаемым ~Р/Т₂. В этом случае при N = 8,82 • 10¹⁹ м~³ из уравнений (8) по аналогии с работой [7] получим задачу на собственные значения для коэффициента усиления:

Л = К//1 ■ [®^/(ЗЙ^о)]1/2 ~ 5,3 • 1011 с"1.

Применительно к задаче усиления излучения коэффициент усиления будет порядка Г = с! Л ~ 5,6 • 10^-4 м, где длина волны X = 2лс / <в « 4,0 ■ 10~⁵ м. Видно, что условие приближения медленно меняющейся амплитуды выполняется.

Из полученных результатов следует, что предположение медленно меняющейся амплитуды поля излучения действительно имеет место.

В качестве нестационарного поля, которое включается «мгновенно», можно использовать поле [10, 11] длительностью AZ = 3 • 10-9 с, с шириной переднего фронта АГ «10~*° с. Предвари тельно проведенные численные расчеты показывают, что для такого поля также имеет место процесс накачки среды для усиления излучения.

Математическое моделирование процесса усиления излучения. Достоверность утверждений о возможности усиления электромагнитного излучения в среде, насыщенной нанотрубками, в немалой степени зависит от достоверности результатов решения системы уравнений (8).

Численные значения параметров, входящих в систему уравнений (8), в системе единиц SI имеют такие значения, что различие в коэффициентах уравнений (8) составляет величину ~ 1050. Данное обстоятельство указывает на то, что система дифференциальных уравнений (8), по-видимому, принадлежит к классу сверхжестких дифференциальных уравнений.

По этой причине для численного решения системы (8) была предпринята попытка решить ее с помощью неявного метода Рунге-Кутгы-Грина [9]. Этот метод представляет собой многошаговую численную процедуру 5-го порядка аппроксимации, использующую дифференцирование назад для вычисления матрицы Якоби. В том виде, в каком представлены уравнения (8), решение с помощью указанного численного метода получить не удалось.

После введения новой переменной П = — Р и перехода от системы единиц SI к другой системе единиц, учитывающей характерные масштабы времени и размеров данной задачи, а именно: за единицу времени принято 10 ⁹ с, длины 10“⁹ м, массы КГ⁶ кг - решение системы уравнений (8) стало возможным. В качестве начальных условий для уравнений (8) задавались следующие значения: удельная энергия ^ = O,5f_o |£|²=10”⁴Дж/м³, населенности ?У = 1,0-10²⁰м~³ и N_o = 0,5-10^й м^-3, поляризация полагалась равной нулю. Расчеты проводились до момента времени / =3 • 10”⁹ с , их результаты представлены на рис. 1-3. На рис. 1 (график с разрывом на оси абсцисс) приведены результаты расчетов энергии W(t) физической системы по уравнениям (8). На начальном участке 0 <  t < 1,5 • 10”⁹ с график функции W (?) имеет быстро осциллирующий характер.

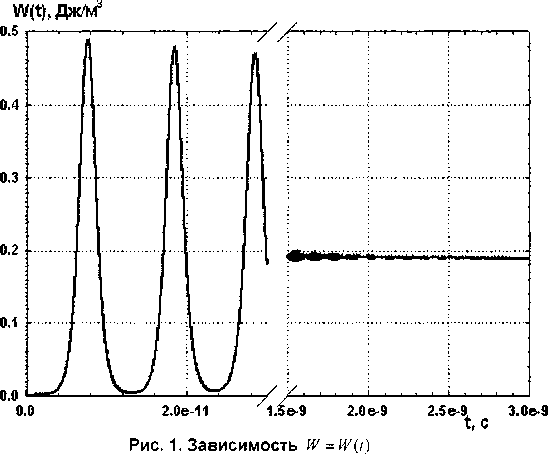
Для выяснения вопроса о природе осцилляций, появляющихся у решений системы уравнений (8) данной работы: то ли они имеют физический смысл, то ли это паразитные колебания, обусловленные численным методом решения - был проведен следующий численный эксперимент. На отрезке 0 < ? < 2,5 • 1 (Г¹¹ с решались уравнения с шагами вычисления функций по времени М_х и А?₂, отличающимися друг от друга в 1000 раз.

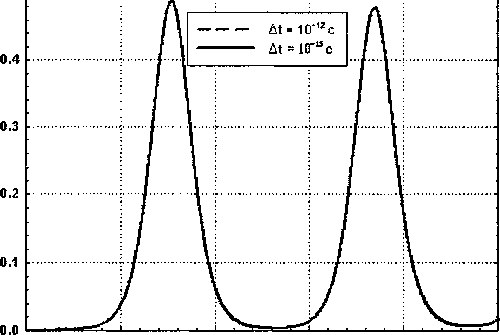
Если бы колебания функции имели паразитный характер, то графики функции WO) отличались бы для разных шагов А?] и А?₂ как по характеру осцилляций, так и по размаху колебаний. Результаты расчетов численного эксперимента приведены на рис. 2.

Рисунок показывает, что функции, рассчитанные на сильно отличающихся разностных сетках, совпадают вполне. Отсюда делается заключение о том, что колебательный характер поведе- ния решения обусловлен физическим механизмом. Осциллирующий характер N(t) и ^(t) объясняется взаимодействием излучения со средой, в соответствии с законом сохранения энергии. Интересно поведение функции населенности N(t), представленной на рис. 3.

W(t), дом3

0.5

0.0

Рис. 2. Зависимость Д' = W(p. Расчеты проводились с разными шагами по времени такими, что отношение Ы_х[М_г = 1000

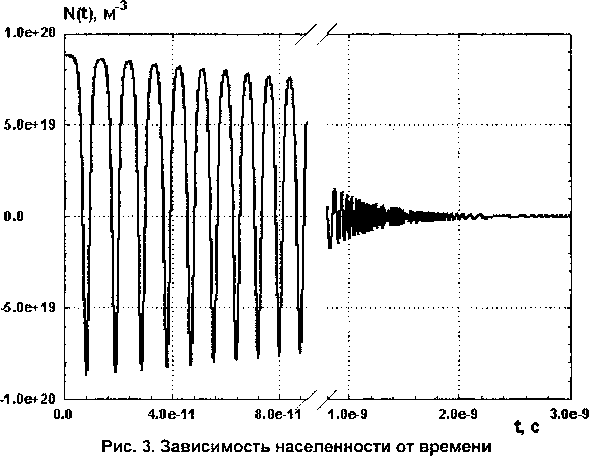
Колебания происходят от отрицательных значений N(f) до положительных, затухая по амплитуде с увеличением времени. И при значениях времени Z > 10 ⁸ с населенность ZV(O устанавливается около значения N_o ~ 10¹¹ м ³. Объяснение механизма колебательного характера решения N(f) системы уравнений (8) приведено выше.

Обсуждение результатов. В работе на основе квантового подхода теоретически показана возможность генерации излучения с длиной волны К ~ 4-10"⁵ м = 40 мкм на основе удлиненных наночастиц с поперечной ориентацией оси симметрии относительно нестационарного поля. При £о ⁼ 3-10⁴ В/м, R = 10“⁸ м, L = 10⁷ м и объемной доле частиц Со = 10² плотность энергии генерируемого излучения W ~ 0,2 Дж/м³. Плотность генерации излучения можно увеличить в десятки раз, если линейные размеры уменьшить в несколько (например, в три раза). Но при этом величину нестационарного поля нужно увеличить в три раза (REq = const).

Оценки показывают, что рассмотренный в работе подход можно обобщить на случай, когда нестационарное поле будет ориентировано вдоль оси наночастиц. В этом случае при длине наночастиц L = 10'⁶ м длина волны усиливаемого излучения будет порядка миллиметра. В такой постановке нужно будет использовать многоуровневую модель.

Авторы благодарят М.И. Яландина за помощь в подборе параметров квазистационарного поля; В.Г. Елецкого - за консультацию по нанотрубкам; А.Н. Еняшина - за консультацию по нанотрубкам и предоставленную литературу по данной тематике.

Работа выполнена по проекту РФФИ № 10-02-96012.