Квантовые и волновые характеристики пространственно-энергетических взаимодействий

Квантовые представления о строении атомов и молекул составляют фундамент современных естественно-научных теорий. Так, в стационарном состоянии момент количества движения электрона равен целому кратному от постоянной Планка. Это главное квантовое число и еще три других в целом однозначно характеризуют состояние любого атома. Кратность атомных квантовых характеристик проявляется и в спектральных данных для простых и сложных структур.

Известно также, что любые сложные по форме периодические процессы могут быть представлены в виде отдельных про- стых гармонических волн. «По теории, доказанной Фурье, колебания любой формы с периодом Т можно представить как сумму гармонических колебаний с периодами Т1, Т2, Т3, Т4 и т. д. Зная форму периодической функции, можно вычислить амплитуду и фазы синусоид, суммированием которых может быть данная функция» [6].

Поэтому многие закономерности межмолекулярных взаимодействий, комплексообразования и нанотермодинамики объясняются с применением функциональных кратных квантовых или волновых энергетических характеристик структурных взаимодействий.

В данном исследовании делается попытка использовать в этих целях представ- ления о пространственно-энергетическом параметре (Р-параметре).

О двух принципах сложения энергетических характеристик взаимодействий

Анализ кинетики разнообразных физикохимических процессов показывает, что во многих случаях складываются обратные величины скоростей, кинетических или энергетических характеристик соответствующих взаимодействий.

Некоторые примеры: амбиполярная диффузия, суммарная скорость топохимической реакции, изменение скорости света при переходе из вакуума в данную среду, эффективная проницаемость биомембран.

В частности, такое предположение подтверждается формулой вероятности процесса переноса электрона ( W „ ) за счет перекрывания волновых функций 1 и 2 (в стационарном состоянии) при электронно-конформационных взаимодействиях:

где Е – полная энергия системы, первый и второй члены – кинетические энергии частиц, третий член – потенциальная энергия между частицами 1 и 2, вектора r ₂ и r 1 характеризуют расстояния между частицами в конечном и начальном состояниях.

Для движущихся термодинамических систем первое начало термодинамики имеет вид [11]:

5 Е = d

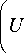
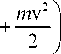
±5 A ,

где 5 Е - количество энергии, сообщенное системе;

, (     mv2 | член d I U + I характеризует изменения внутренней и кинетической энергий системы; + 5A - работа, выполненная системой; - 5A - работа, совершенная над системой.

Так как величина работы численно равна изменению потенциальной энергии, то

+5 А = -A U и -5 A = +A U .     (6, 7)

w ~

1 W 1 W 2

2 W 1 + W 2

Уравнение (1) используется при оценке характеристик процессов диффузии, сопровождающейся безызлучательными переносами электронов в белках [9].

«Из классической механики известно, что относительное движение двух частиц с энергией взаимодействия U ( r ) происходит как движение материальной точки с приведенной массой µ :

Вероятно, не только в термодинамических, но и во многих других процессах в динамике взаимодействия движущихся частиц важно не только значение потенциальной энергии, но и ее изменение. Поэтому по аналогии с уравнением (4) должно выполняться уравнение для двухчастичных взаимодействий:

= — + —

ц   m 1   m 2

в поле центральной силы U ( r ), а общее поступательное движение – как свободное движение материальной точки с массой:

5Е = d | m1v^ + m2v2 l + A U(8)

( 2      2 J .

Здесь

A U = U2 - U 1,(9)

где U ₂ и U ₁– потенциальные энергии системы в конечном и начальном состояниях.

m = m ₁ + m 2 .

Такое положение вещей имеет место и в квантовой механике» [3].

Задача двухчастичных взаимодействий, происходящих по линии связи, была решена еще во времена Ньютона и Лагранжа:

Е = m^ + ф + U ( 4 - Г. ),       (4)

При этом отсчет полной энергии (Е) и (mv21                 _ кинетической энергии I -2- I может идти с их нулевого значения, и тогда в уравнении (4) модифицируется только последний член.

Был проведен анализ характера изменения величины потенциальной энергии ( A U) по ее знаку для различных потенциальных полей, приведенный в таблице 1.

Таблица 1

Направленность процессов взаимодействий

№	Системы	Вид по-тенциаль-ного поля	Процесс	U	r 2 r 1 ( x 2/ ) ( / x J	U 2 U 1	Знак A U	Знак δ A	Направление процесса в потенциальном поле
1	Разноименные электрические заряды	электро-статиче ское	притяжение	- kqq r	r 2 <  r 1	U 2 >  U 1	-	+	по градиенту
			отталкива ние	- k^ r	r 2 >  r 1	U 2 <  U 1	+	-	против градиента
2	Одноименные электрические заряды	электро-статиче ское	притяжение	k q 1 q 2 r	r 2 <  r 1	U 2 >  U 1	+	-	против градиента
			отталкива ние	k q 1 q 2 r	r 2 >  r 1	U 2 <  U 1	-	+	по градиенту
3	Элементарные массы m 1 и m 2	гравитационное	притяжение	mm - Y —— r	r 2 <  r 1	U 2 >  U 1	-	+	по градиенту
			отталкивание	mm - Y — r	r 2 >  r 1	U 2 <  U 1	+	-	против градиента
4	Деформация пружины	поле упругих сил	сжатие	, A x 2 k 2	x 2 <  x 1	U 2 >  U 1	+	-	против градиента
			растяжение	, A x 2 k 2	x 2 >  x 1	U 2 >  U 1	+	-	против градиента
5	Фотоэффект	электро-статическое	отталкива ние	k q 1 q 2 r	r 2 >  r 1	U 2 <  U 1	-	+	по градиенту

Из таблицы 1 видно, что значения - A U и соответственно + 8 A (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а A U и - 8 A (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.

Решение двухчастичной задачи взаимодействий двух материальных точек с массами m ₁ и m ₂, полученное при условии отсутствия внешних сил, соответствует взаимодействиям, которые идут по градиенту, работа положительная, совершается системой (аналогично процессу притяжения в гравитационном поле). Решением этого уравнения через приведенную массу ( ц ) является [8] уравнение Лагранжа для относительного движения изолированной системы двух взаимодействующих материальных точек с массами m₁ и m₂ , которое в координате х имеет вид:

При этом x" = а (характеристика ускорения системы). Для элементарных участков взаимодействий А х можно принять:

d U ~ A U d x    A x

То есть

ц a Ax = -A U

И тогда:

1/( a A x ) (1/ m i + 1/ m 2 )

~-A U ■

1/( m 1 a Ax ) + 1/( m 2 a Ax )

« -A U

.

Или

A U

~1

A U 1   A U ₂ ,

.   8 U ц x = -—;

о x

=-- 1--.

ц   m i   m _г

где U – взаимная потенциальная энергия материальных точек; ц - приведенная масса.

где A U 1 и A U 2 - потенциальные энергии материальных точек на элементарном участке взаимодействий, A U - результирующая (взаимная) потенциальная энергия этих взаимодействий.

Таким образом, можно сделать следующие выводы:

1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа), результирующая потенциальная энергия находится по принципу сло-

жения обратных значений соответствующих энергий подсистем [19]. Аналогично рассчитывается приведенная масса для относительного движения изолированной системы двух частиц.

• 2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа), выполняется алгебраическое сложение их масс и соответствующих энергий подсистем (аналогично гамильтониану).

Исходные критерии

Из уравнения (10) следует, что результирующая энергетическая характеристика системы взаимодействия двух материальных точек находится по принципу сложения обратных величин исходных энергий взаимодействующих подсистем.

«Электрон с массой m, движущийся около протона с массой М, эквивалентен части-mM це с массой: тпр =------» [10, с. 12].

т + M

Поэтому, модифицируя уравнение (10), можно предположить, что энергия валентных орбиталей атома (ответственная за межатомные взаимодействия) может быть рассчитана [19] по принципу сложения обратных величин некоторых исходных энергетических составляющих согласно уравнениям:

• 1      1 _ 1       1 _ х 1

q²⁺ Wn "  Р э ™^И P о q^{2 +} Wrn

P э _ P о/ r i (11), (12), (13)

где W – орбитальная энергия электронов [16]; r – орбитальный радиус -й орбитали [20]; q = Z*/n* – по [13; 14], n – число электронов данной орбитали, Z* и n* – эффективный заряд ядра и эффективное главное квантовое число, r – размерные характеристики связи.

Величина Р ₀ названа пространственноэнергетическим параметром (ПЭП), а величина Р _Э – эффективным Р -параметром (эффективный ПЭП). Эффективный ПЭП имеет физический смысл некоторой усредненной энергии валентных электронов в атоме и измеряется в единицах энергии, например, в электрон-вольтах (эВ).

Значения Р0-параметра являются табулированными постоянными величинами для электронов данной орбитали атома.

Для размерности ПЭП можно записать:

[ Р оИ q И 41 r ] _ [ 4И= кМ _ дж".

с где [E], [h] и [v] - размерности энергии, постоянной Планка и скорости.

Введение Р -параметра следует рассматривать как последующее развитие ква-зиклассических представлений с использованием квантово-механических данных по строению атома для получения критериев энергетических условий фазообразования. При этом для систем одноименно-заряженных (например, орбитали в данном атоме) однородных систем сохраняется принцип алгебраического сложения таких параметров:

z Р Э = к Р о/ r i ) ;       ^ Р Э ^_ ^ Р . (14), (15)

или:

z р о _ p 0 + p 0 + p 0 '' + ...^; r z p э ^_z р о ,⁽¹⁶⁾,⁽¹⁷⁾

где Р -параметры суммируются по всем валентным орбиталям атома.

Для вычисления значения Р _Э-параметра на данном расстоянии от ядра в зависимости от вида связи вместо r может использоваться или атомный радиус ( R ), или ионный радиус ( r _И).

Кратко о достоверности такого подхода. Как показали расчеты, величины Р _Э-параметров численно равны (в пределах 2 %) полной энергии валентных электронов ( U ) по статистической модели атома. Используя известное соотношение между электронной плотностью ( в ) и внутриатомным потенциалом по статистической модели атома [5], можно получить прямую зависимость Р _Э-параметра от электронной плотности на расстоянии r_i от ядра.

Рациональность данной методики была подтверждена путем расчета электронной плотности с использованием волновых функций по Клементи [15] и сопоставлением ее с величиной электронной плотности, вычисленной через значение Р _Э-параметра.

Волновое уравнение Р -параметра

Для характеристики пространственноэнергетических свойств атома введены два вида Р-параметров, связь между которыми Р простая: - = —, где R - размерная характеристика атэомаR.

Учитывая дополнительные квантовые характеристики подуровней в атоме, это уравнение в координате х можно записать как ар          ар.

АР •=или дРэ = д-0, э Ах         э дх ’ где величина АР равна разности между Р0-парамет-ром i-й орбитали и РОТ – параметром отсчета (параметром основного состояния при данном наборе квантовых чисел).

Согласно установленному [19] правилу сложения Р -параметров одноименно-заряженных или однородных систем для двух орбиталей в данном атоме с разными квантовыми характеристиками и в соответствии с законом сохранения энергии получаем:

А-"-А-' =- „ э э     э,Х, где РЭ Х - пространственно-энергетический параметр квантового перехода.

Приняв за размерную характеристику взаимодействия АХ = А х , имеем:

АP 0 АP 0 _ P о „АP 0 АP 0 _ P 0Х =или=.

АХ АХ АХ АХ АХ АХ

Разделим еще раз почленно на АХ :

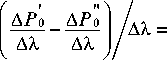
P 0

АХ 2, где

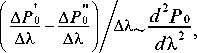
d2 P о + P о ~ 0 dХ2 АХ2~

Учитывая только те взаимодействия, при которых 2 пА х = АХ (замкнутый осциллятор), получаем уравнение:

d ² P 0 dx ²

+ 4 п ² P^ ~ 0, АХ ²

h       d ² P 0     2 P 0 2 2

Так как ах = —, то    ₂ ⁺ 4п -у m v ” ⁰

mv     dx h или

d P0 , 8n m D с - о

-ГТ + ,2 P 0 Ek = 0

dx h

mV 2

где Ek = —---кинетическая энергия электрона,

Уравнение Шредингера для стационарного состояния в координате х :

d^ Sim „ Ek = 0, dx h

Из сравнения этих двух уравнений следует, что Р ₀-параметр численно коррелирует с величиной Т -функции: Р _о ® Т , а в общем случае ей пропорционален: Р о ~ Т . Учитывая широкие практические возможности применения методологии Р -параметра, можно считать этот критерий материализованным аналогом Т -функции [17; 18].

Так как Р ₀-параметры, как и Т -функ-ция, обладают волновыми свойствами, то для них должны выполняться принципы суперпозиции, что определяет линейный характер уравнений сложения и изменения Р -па-раметров.

Квантовые свойства Р -параметра

Согласно Планку энергия осциллятора ( Е ) может принимать только дискретные значения, равные целому числу элементарных порций – квантов энергии:

nE = h v = hc / Х , (19)

где h - постоянная Планка, v - частота электромагнитной волны, с - ее скорость, Х - длина волны, n = 0, 1, 2, 3…0

Уравнение Планка также дает строго определенную связь между двумя способами описания явлений природы – корпускулярными и волновыми.

Р ₀-параметр, как первичная энергетическая характеристика структурных взаимодействий, аналогично уравнению (19) может иметь простую зависимость от частоты квантовых переходов:

P 0 -A (Xv 0 > , (20)

где X - длина волны квантового перехода [1]; ^ = h /(2 π ); ν ₀ – кайзер, единица волнового числа, равная 2,9979∙10¹⁰ Гц.

Согласно уравнению Ридберга произведение правой части этого уравнения на величину (1/ n ² – 1/ m ² ), где n и m – главные квантовые числа, должно дать постоянную величину. Поэтому может выполняться уравнение:

P о (1/ n ²i - V m ²i ) = N MXv о )(1/ n ² - V m ²), (21)

в котором постоянная величина N имеет физический смысл волнового числа и является равной для атома водорода: 2∙10²Å^-1.

Соответствующие расчеты приведены в таблице 2, где r_i ′ = 0,5292 Å – орбитальный радиус 1S-орбитали и r_i ^″ = 2² ∙ 0,5292 = 2,118 Å– это значение примерно равно орбитальному радиусу 2S-орбитали.

Величина Р ₀-параметра получена по уравнению (12), например, для 1S-2P перехода:

1/ P ₀ = 1/(13,595∙0,5292) + 1/14,394 → P₀ = 4,7985 эВÅ.

Значение q ² взято по [13; 14], для электрона в атоме водорода оно численно равно произведению энергии покоя на классический радиус.

Точность полученных соотношений находится в пределах относительной погрешности 0,06 (%), то есть формула (21) работает в пределах точности самих исходных данных.

В уравнении (21) тоже есть связь между квантовыми характеристиками структурных взаимодействий частиц и частотами соответствующих электромагнитных волн.

Но в данном случае имеется зависимость между пространственными, распространенными по координате параметрами. Так, у Р0-парамет-ра эффективная энергия умножается на размерную характеристику взаимодействий, а в правой части уравнения (21) величина кайзера умножается на длину волны квантового перехода.

В таблице 2 показана возможность применения уравнения (21) и для комптоновской длины волны электрона ( λ _к = 2,4261∙10 ^-12 м), которое в этом случае принимает вид:

P o = 10⁷ MX k V o )               ⁽²²⁾

(с относительной погрешностью 0,25 %).

Целочисленные десятичные значения выявляются и при анализе соотношений в системе «протон – электрон» (см. табл. 3).

• 1.    Протон в ядре , энергии трех кварков: 5+ 5 + 7 ≈ 17 (МэВ) → Р_р ≈ 17 МэВ ∙ 0,856 ∙ ∙ 10^-15 (м) ≈ 14,552 ∙ 10^-9 эВм. Аналогично для электрона Р_е = 0,511 (МэВ) ∙ 2,8179 ∙ 10^-15 (м) (классический радиус электрона) → Р_е = = 1,440 ∙ 10^-9 эВм.

• 2.    Свободный протон Р _n = 938,3 (МэВ) ∙ ∙ 0,856 ∙ 10^-15 (м) = 8,0318 ∙ 10^-7 эВм. Для электрона в атоме: Р_а = 0,511 (МэВ) ∙ 0,5292 ∙ 10^-5(м) = = 2,7057 ∙ 10^-5 эВм.

Поэтому Р_р ≈ 10 Р_е .              (23)

И тогда 3Р_а ≈ 10²Р _n .               (24)

Относительная погрешность расчетов по этим уравнениям находится в пределах точности исходных данных для протона ( δ ≈ 1 %).

Из таблиц 2 и 3 следует, что волновое число N квантуется по десятичному принципу:

N = n10Z, где n и Z – целые числа.

Таблица 2

Квантовые свойства параметров атома водорода

Орбитали	Wi (эВ)	ri (Å)	qi 2 (эВÅ)	Р 0 (эВÅ)	Р 0(1/ n 12 – 1/ m 12) (эВÅ)	N (Å-1)	λ (Å)	Кванто вый переход	Nhλν0 (эВÅ)	Nhλν 0 (1/ n 2 – 1/ m 2) (эВÅ)
1S	13,595	0,5292	14,394	4,7985	3,5989	2•102	1 215	1S-2P	4,7951	3,5963
1S						2•102	1 025	1S-3P	4,0452	3,5954
1S						2•102	912	1S-nP	3,5990	3,5990
2S	3,3988	2,118	14,394	4,7985	3,5990	2•102	6 562	2S-3P		3,5967
2S						2•102	4 861	2S-4P		3,5971
2S						2•102	3 646	2S-nP		3,5973
1S	13,595	0,5292	14,394	4,7985		107	2,4263•10-2	–	4,7878

Таблица 3

Квантовые соотношения параметров протона и электрона

Частица	Е (эВ)	r (Å)	Р = Еr (эВÅ)	Соотношения
Протон свободный	938,3•106	0,856•10-5	8,038•103 = P n	3P a /P n ≈ 102
Электрон в атоме	0,511•106	0,5292	2,7042•105 = P a
Протон в ядре атомов	(5 + 5 + 7)•106 = 17•106	0,856•10-5	145,52 = P p	P p /P e ≈ 10
Электрон	0,511•106	2,8179•10-5	14,399 = P e

Можно отметить и другие примеры уравнений электродинамики, в которых есть целочисленные десятичные функции, например, в формуле

4pε0с2 = 107, где ε0 – электрическая постоянная.

В работе [2] получено выражение зависимости постоянных величин электромагнитных взаимодействий от значения Р _е-параметра электрона:

k µ ₀c = k/( ε ₀c) = P_e^1/2c² ≈ 10/ α, (25)

где k = 2 π / J 3; µ ₀ – магнитная постоянная; с – электромагнитная постоянная; α – постоянная тонкой структуры.

Все вышеприведенные выводы основаны на применении достаточно точных формул в пределах точности самих исходных данных.

Выводы

• 1.    Два принципа сложения энергетических характеристик взаимодействия функционально определяются направлением взаимодействия по градиенту потенциала (положительная работа) или против градиента потенциала (отрицательная работа).

• 2.    Получено уравнение зависимости пространственно-энергетического параметра от спектральных и частотных характеристик в атоме водорода.