Квантовые ограничения восприятия удаленных излучающих объектов

Квантовые свойства электромагнитных излучений приводят к известным проблемам в задачах регистрации слабых оптических сигналов. При уменьшении энергии сигнала до уровня одного кванта и ниже сигнал становится дискретным (прерывистым) и имеет место (воспринимается фотоэлектронным умножителем) лишь с определенной вероятностью [1; 2].

Поскольку квантовые свойства в принципе присущи всем видам электромагнитного излучения, то аналогичные эффекты дискретизации сигналов естественно ожидать во всех частотных диапазонах, включая радиолокацию [3].

Следует заметить, что загадочную альтернативу квантово-волнового дуализма в принципе принято разрешать в пользу волновой интерпретации излучений. Классическим доказательством последней считается опыт [4], в котором явление дифракции (т. е. волновые свойства) потока электронов сохранялось, несмотря на то что электроны пролетали поодиночке (т. е. взаимодействовать не могли). Естественно, что для получения дифракционной картины на фотопластинке (при пониженной таким образом интенсивности потока) время экспозиции было соответственно увеличено. То есть суммарная энергия излучения была оставлена на достаточном уровне.

В связи с множеством толкований этого вопроса хотелось бы подчеркнуть, что никакие смыс- ловые (ни физические, ни гносеологические) интерпретации квантово-волнового дуализма не входят в тематику данной статьи. Квантовые свойства излучений представляются неизбежными как техническая проблема приема слабых электромагнитных сигналов (энергии, соизмеримой с квантом). Но, несмотря на такие сугубо практические основания, квантовые свойства влекут за собой определенные последствия для фундаментальных представлений о воспринимаемом физическом мире.

Примечательным представляется, например, тот факт, что «бесконечно малых» электромагнитных сигналов не бывает в смысле существования такого уровня малости, ниже которого сигналы не могут быть, по крайней мере, обнаружены. При этом проблема различимости слабых сигналов оказывается связана не только с традиционным отношением сигнала к шуму, но и с менее привычным вопросом о существовании сигнала как такового.

Нижний предел физического существования слабых сигналов рассматривается в статье [3] применительно к активной локации, которая характеризуется уменьшением энергии сигнала с 4-й степенью расстояния. Непосредственное же восприятие излучений от источников разного рода относят к пассивной локации, характеризуемой уменьшением энергии с квадратом расстояния. Пассивная локация представляет интерес в связи с многообразием ее видов как в естественной природе (см., напр., [5]), так и в технике (см., напр., [6–8]).

Особо интересным видом пассивной локации представляется восприятие излучающих космических объектов. Колоссальность космических расстояний (реальная бесконечность пространства) неизбежно делает «бесконечно малыми» излучения космических тел любого конечного размера и температуры. При этом необходимым условием для того, чтобы хотя бы просто «увидеть» (в оптическом или ином диапазоне) удаленное светило, является возможность приема от него хотя бы одного кванта излучения.

Энергию E_r воспринятого излучения можно представить в виде

Er= fr∆ωste, (1) где fr – интенсивность воспринимаемого излучения; ∆ω – частотный диапазон; s и te – апертура приемного устройства и продолжительность экспозиции (время наблюдения). При этом интенсивность fr излучения, воспринимаемого от одиночного источника (светила), может быть представлена произведением вида fr= Aft, (2) где ft – интенсивность излучения на поверхности источника (его испускательная способность); A – коэффициент пространственного ослабления интенсивности (см. далее); а при измерениях анизотропного фона (которому не приписывается определенный источник и который имеет одинаковую интенсивность во всех направлениях) интенсивность fr представляет произведение вида fr= ad fb, (3) 4π где fb – интенсивность фона; ad – телесный угол, характеризующий направленность приемного устройства.

Итак, будем полагать, что для волновой интерпретации результатов измерения любых излучений необходимо, чтобы энергия E_r воспринятого излучения была не меньше энергии кванта.

1. Спектральный анализ интенсивности излучения квантов

Мощность излучения с единицы поверхности абсолютно черного тела, разогретого до абсолютной температуры T, описывается функцией ft = f(ω, T) испускательной способности (функцией Кирхгофа), которая характеризует спек- тральный состав равновесного теплового излучения по круговой частоте ω. Выражение функции f(ω, T), известное как формула Планка, имеет вид [9; 10]

,      4П2с2 exp(hto / kT) - 1 , где c = 299792458 м/с – скорость света; k = 1.380658 ⋅ 10-23 Дж/К – постоянная Больцмана; Й = 1.054571628 ■ 10-34 Дж ■ с ■ рад-1 — постоянная Планка.

При этом мощность, излучаемая в диапазоне [ ω ₁, ω ₂], может быть представлена определенным интегралом вида

ω ₂

F ( ∆ω , T ) = ∫ f ( ω , T ) d ω ,                           (5)

ω ₁

а суммарная излучаемая мощность определяется законом Стефана – Больцмана:

∞

∫ f ( ω , T ) d ω = σ T ⁴,                                (6)

где

σ= π ^k = 5.670 ⋅ 10 ^{- 8} Дж ⋅ с ^{- 1} ⋅ м ^{- 2} ⋅ К ^{- 4}.

60 с ² Й 3

Частота fe = ωπe Гц максимума излучаемой энергии (получаемая путем приравнивания нулю производной функции (4) Планка и решения этого уравнения с помощью W-функции Ламберта) определяется соотношением fe= aeT,                                             (7)

где a_e = 5.879 ⋅ 10¹⁰. При этом длина волны λ _e (м) этого максимума (для закона Планка в виде f_t = f ( λ , T ), т. е. переписанного для длин волн – см., напр., [9]) аналогичным образом получается в виде соотношения

λ e = b e _T ¹ ,                                           (8)

в котором b_e = 2.89777 ⋅ 10 ^{- 3}. Зависимости (7), (8) максимума излучения от температуры T называются законом смещения Вина. (Значения f_e и λ _e при данной температуре T не связаны между собой общим соотношением λ= с / f .)

Для перехода от анализа спектра мощности к анализу спектра квантов достаточно разделить спектр f ( ω , T ) излучаемой мощности на энергию Б = Й ю излучаемых квантов. В результате имеем выражение квантового спектра q ( ω , T ) в виде 2

q ( ω , T ) =ω             ¹          ,                    (9)

_п ² _с ² exp( Й to / kT ) - 1

позволяющее представить число квантов, излучаемых в диапазоне [ ю 1 , © 2 ], определенным интегралом вида

® 2          22

Q(Аю, T) = —г f-----ю------ п2c2 ехр(Йю / kT) - 1 ю1

Нормирование спектра q ( ю , T ) (9) дает функцию q d ( ю , T ) плотности вероятностей распределения квантов по частоте ю , т. е.

А-1

q d ( ю , T ) = q ( ю , T )

J q (ю, T) d ю ч 0

При замене ю = (kT / Й)x переменной выраже- ния (9), (10) приводятся к виду 2

q (x, T) = KT 3

exp x - 1

Q (А x, T) = KT31 (x1, x2), где x2

x ² dx

I ( xb x2) = exp x - 1

x ₁

причем константа

K = ⁽ k / ^{Й 1} = 2,529816 ■ 10¹⁵ 4 л ² c ²

имеет надлежащую размерность

1    1рад

32    .

град3м2с

Неопределенный интеграл x2dx exp x - 1

имеет решение вида 2

------dx = 2 xLi₂(e x ) - 2 Li ₃( e x ) - exp x - 1

x ³

—3- ^{+ x} lo^{g(1 - e} ) ⁺ C,

(где функция Li_n ( x ) – полилогарифм [11]), позволяющее вычислять значения определенного интеграла I ( x ₁, x ₂).

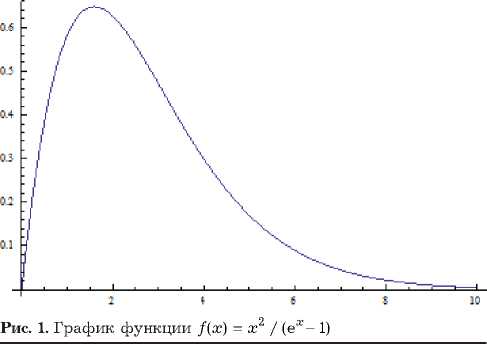
Поскольку функция x2 / (ex -1) (см. рис. 1) имеет максимум при Xqf = 1.59362, то максимум функции интенсивности (9) испускания квантов имеет место при частоте f = юq Гц, определя-q 2п емой выражением вида

k fq = 2лй xqfT = aqT ’

где aq

— xqf = 3.3206 ■ 10¹⁰ -1—1—.

2 п Й                   с град

При переписывании выражения (9) спектральной плотности излучения квантов в виде q(X, T) для длин волн задача вычисления длины волны Xq (м) квантового максимума (по аналогии с энергетическим максимумом для длин волн) сводится к нахождению максимума функции x4(exp x - 1)

Дифференцирование этой функции и решение соответствующего уравнения (аналогично выводу соотношений (7), (8), (15)) дает Xqх = 3.92069 и, соответственно, х q = bq T ’

где

= 2 л й с = ₃.66968 ■ ю- S .

q kTx q x

Сравнение выражений (15) с (7) и (16) с (7) показывает, что частота f_q квантового максимума в a_e / a q ® 1.77 раз меньше частоты f_e энергетического максимума, а длина волны X q квантового максимума в b q / b e « 1.27 раз больше длины волны X _e энергетического максимума.

Коэффициент A пространственного ослабления интенсивности излучения шарообразного разогретого тела радиусом r с расстоянием R можно представить как отношение площади 4 п r ² излучающей поверхности тела к площади

A =

vme v

P { ц = m } =         ,                            (19)

m !

представляющее вероятность P { ц = m } приема m квантов в единицу времени.

Возможность восприятия далекой звезды может быть оценена либо из условия

V> f min ,                                     (20)

где fmin – минимальная допустимая частота мерцания изображения звезды, либо из условия vte > mq                                     (21)

регистрации не менее порядка m_q квантов в среднем за время t_e экспозиции.

Из выражений (18), (17) и (13) очевидно расчетное соотношение для интенсивности V в виде ²

v = KT ³ s 1 — 1 I ( x 1 , x ₂).                          (22)

I R )

Из выражения (22) и критериев (20) или (21) условие видения звезды радиуса r можно записать как

R max = ЦКТ 3 1 ( X 1 , X 2 ) s / f min , (23) или

R max = ЦКТ 3 1 ( X 1 , X 2 ) st e / m_e (24) соответственно.

Необходимым условием обнаружения удаленного небесного тела является регистрация хотя бы одного излученного им кванта. Подставляя в неравенство (24) значения I (0, да ) = 2.40411 и m e = 1, имеем максимальное расстояние R _max w принципиальной обнаружимости небесного тела радиусом r и температуры T при экспозиции st_e во всем диапазоне частот to электромагнитных излучений

R max, w = —^Т 3 st e , (25) где W = KI (0, да ) = 6.082 ■ 10¹⁵. Выражение (25) представляет предельные возможности обнаружения удаленных светил, поскольку подразумевается такое приемное устройство (неизвестное современной науке), которое способно зарегистрировать квант во всем диапазоне частот от нуля до бесконечности.

• 2.    Обсуждение результатов.

Примеры численных оценок

Пример 1

Оценим пространственные пределы видения Солнца ( — = 6.96 ■ 10 8 м, эффективная температура T поверхности равна 5780 К [12, т. I, с. 15–16]).

При таких параметрах неравенство (25) имеет вид

R max, w = 2.4 ■ 10 22 JSTe .                       (26)

При эффективной площади s = 10 м² приемного устройства и времени экспозиции t_e = 10 с принципиальная возможность приема кванта от звезды, подобной Солнцу, ограничивается рас- 20                       7

стоянием около 2.4 ■ 10 км, или 2.3 ■ 10 световых лет.

Заметим, что оценки вида (25)–(26) пригодны для обоснования отрицательных утверждений – о невозможности обнаружения слишком далеких светил, поскольку в этих оценках подразумевается «антенна», способная воспринимать электромагнитные излучения всех видов (в неограниченном диапазоне частот). Оценка же возможностей реальных технических средств наблюдения требует вычисления интенсивностей излучения в конечных частотных диапазонах, т. е. использования критериев (23) или (24), включающих в себя значения I(x1, x2). Примеры этих значений приведены (при ряде температур небесного тела) для принятых спектральных диапазонов (рентгеновского, ультрафиолетового /УФ/, видимого оптического, инфракрасного /ИК/ и радио) в таблице. Аргументы x связаны с длинами волн X и температурой Т соотношением x1,2 =

D 1

Т X/

где

_ Й2лс _ _    9

D =----- = 1.438767 ■ 10^-2 град ■ м.

k

В той же таблице приведены значения частот f_e , f q и длин волн X _e , X q максимумов излучения при данных температурах тела.

Пример 2 (с использованием таблицы).

Возвращаясь к вопросу о пространственных пределах видения Солнца, можно оценить предельное расстояние видения подобной звезды невооруженным глазом с помощью таблицы. Положим, что хрусталик глаза аккомодируется в ночной темноте до диаметра порядка 1 см (т. е. эффективная площадь s составляет около

• — 4 2

10 м ), а минимальная допустимая частота f _min мерцания равна 10 Гц. Подставив в выражение (23) табличное значение I ( X 1 , X 2 ) = 0.63 для Т = 5780 К в диапазоне видимого света, получим R _max = 3.87 ■ 10²¹ м ® 4 ■ 10¹⁸ км, т. е., поряд-

Таблица

Параметры максимумов излучения и значения интеграла I ( x ₁, x ₂) для основных спектральных диапазонов при различных значениях температуры небесного тела

Температура, К	Параметры максимумов		Значения I ( x 1, x 2) в спектральных диапазонах ( λ , м)
	f e fq	λ e λ q	Рентг. 10 - 12–10 - 8	УФ 10 - 8–0.4 ⋅ 10 - 6	Видимый свет 0.4 ⋅ 10 - 6–0.76 ⋅ 10 - 6	ИК 0.76 ⋅ 10 - 6–2 ⋅ 10 - 3	Радио 10 - 4–103
5780	3.39 ⋅ 1014	0.50 ⋅ 10 - 6	0	0.106	0.634	1.665	3.07 ⋅ 10 - 4
	1.92 ⋅ 1014	0.63 ⋅ 10 - 6
15000	8.82 ⋅ 1014	0.19 ⋅ 10 - 6	0	1.18	0.713	0.513	4.58 ⋅ 10 - 5
	4.98 ⋅ 1014	0.24 ⋅ 10 - 6
45000	1 2.65 ⋅ 1015 1.49 ⋅ 1015	6.44 ⋅ 10 - 8 8.15 ⋅ 10 - 8	0	2.16	0.166	0.0767	5.11 ⋅ 10 - 6

ка 4 ⋅ 10⁵ световых лет. Это значение примерно в 100 раз меньше значения R _{max, w} , полученного в примере 1 по формуле (26), поскольку теперь речь идет о восприятии кванта, относящегося к конкретному (оптическому) диапазону.

При наблюдении неба через телескоп с объективом диаметром порядка 10 м предельное расстояние видения подобной звезды при тех же прочих условиях может быть увеличено в 10³ раз, достигая 4 ⋅ 10²¹ км и более. В этом случае предельное расстояние уже превышает рассчитанное в примере 1 значение R _{max, w} теоретического предела за счет задания иных параметров st_e экспозиции.

Пример 3

Классические результаты измерения спектра космического фона f_b приводятся в работах [10; 13].

На рис. 2 воспроизведен график [13, рис. 11], имеющий максимум интенсивности, приходящийся на частоту 160.4 ГГц (или длине волны 1.9 мм). Сравнение с аналогичным графиком [10, рис. 5], а также с англоязычными оригиналами обеих нобелевских лекций [10; 13] позволяет

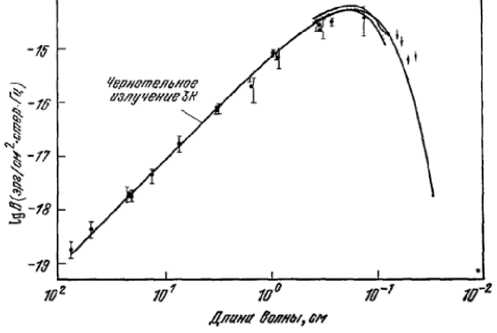
Рис. 2. Результаты измерений спектра космического микроволнового фонового излучения (копия рис . 11 из статьи [13])

устранить неточности в обозначенной на приведенном графике рис. 2 размерности, которая должна быть эрг ⋅ с ^{- 1} ⋅ см ^{- 2} ⋅ стер ^{- 1} ⋅ Гц ^{- 1}. Ту же размерность имеет интенсивность f_b в выражении

E r = f b ^ad ∆ω st e                              (27)

4π

(следующем из соотношений (1) и (3)) для энергии.

По формуле (7) для энергетического максимума указанной частоте 160.4 ГГц соответствует известная абсолютная температура T реликтового излучения, равная 2.73 градуса. Необходимым условием для анализа энергетического спектра (4) (а не квантового спектра (9)) в данной статье принято условие E_r >ε , где E_r – энергия (27) воспринятого излучения, ε – энергия одного кванта, которая для частоты 160.4 ГГц составляет 1.06 ⋅ 10 ^{- 22} Дж (1.06 ⋅ 10 ^{- 15} Эрг). В противном случае (при E_r ≤ε ) температура реликтового излучения должна была бы вычисляться по формуле (15) и составлять 4.83 градуса Кельвина.

К сожалению, в указанных выше источниках не приводятся данные (параметры st_e экспозиции и ширина полосы ∆ω ), которые позволили бы оценить значение энергии (27), воспринятой при измерениях излучений.

Можно предположить, однако, что уровень энергии был достаточно велик, поскольку никакие квантовые эффекты в указанных работах не отмечаются.

Заключение

Из существования квантового порога восприятия излучений следуют пространственные пределы восприятия удаленных излучающих объектов. Эти пределы ожидаемым образом зависят от экспозиции; однако сама возможность существования физически неразличимых излучающих объектов представляет принципиальный интерес.

Достаточно далекие звезды могут быть обнаружены лишь при условии столь продолжительной экспозиции, которая может быть нереализуемой практически. Поэтому пределы восприятия звезд, подобных Солнцу, оценивается 19    22

расстояниями порядка10 –10 км.

Известно [9], что формула Планка получена в предположении о квантовом характере излучения и поглощения энергии. Однако при использовании этой формулы описываемые ею процессы принято считать волновыми.

В связи с этим предложен критерий: считать процессы волновыми, если полученная энергия представлена достаточно большим количеством квантов. Данные об экспозиции оказываются существенны и при использовании этого критерия.

Затронутый вопрос может иметь отношение к интерпретации экспериментов по исследованию реликтового излучения.

Автор благодарен студентам МФТИ Д.И. Глу-ховцу и Я.С. Астафьеву за помощь в использовании вычислительной системы Wolfram Mathe-matica.